基于多目标灰狼算法的H13模具钢铣削工艺优化研究

Research on Optimization of H13 Die Steel Milling Process Based on Multi-Objective Grey Wolf Algorithm

摘要: 模具产品在结构上多为复杂型腔，具有高精度、多特征、难加工等特点，而在模具加工有着显著优势的高速铣削加工，最优的铣削工艺参数选择影响着工件的生产效率、表面质量。首先采用了正交试验设计方法，开展了H13模具钢铣削试验，对结果进行了极差分析，并采用GA-BP神经网络构建了表面粗糙度预测模型；其次，以建立的GA-BP表面粗糙度预测模型和材料去除率为目标函数，相关工艺参数为主要优化变量，基于多目标灰狼优化算法，建立多目标铣削参数优化模型。结果表明，铣削工艺参数对表面粗糙度的影响敏感性排序为：主轴转速 > 切宽 > 进给速度 > 切削深度；所建立的GA-BP神经网络预测模型能够有效预测加工表面粗糙度，平均相对误差为8.72%；并通过实例验证了优化的工艺参数，对比优化前，材料去除率提高了40.1%，表面粗糙度降低了36.4%，加工时间减少了29.3%。

Abstract: Die products are in the structure of complex cavity, with high precision, multi-features, difficult to process and other characteristics, and have a significant advantage of high-speed milling processing in the die processing, the optimal milling process parameters affect the production efficiency of the workpiece, surface quality. Firstly, the orthogonal experimental design method was used to carry out the milling experiment of H13 die steel, the range analysis of the results was carried out, and the GA-BP neural network was used to construct the surface roughness prediction model. Secondly, with the established GA-BP surface roughness prediction model and material removal rate as the objective function and related process parameters as the main optimization variables, a multi-objective milling parameter optimization model was established based on the multi-objective grey wolf optimization algorithm. The results show that the sensitivity of milling parameters to surface roughness is in the order of spindle speed > cutting width > feed speed > cutting depth. The GA-BP neural network prediction model can effectively predict the machining surface roughness, and the average relative error is 8.72%. The optimized process parameters are verified by an example. Compared with before optimization, the material removal rate is increased by 40.1%, the surface roughness is reduced by 36.4%, and the processing time is reduced by 29.3%.

1. 引言

近年来，模具产业已成为我国重要的经济支柱型产业，广泛应用于各种工业装备中。随着国家政策支持以及国内外市场的导向，行业朝着高端精密化方向发展，对生产工艺、设备、加工工具等提出了更高的要求。模具钢是一种硬度高、强度高、耐磨性好的材料，其主要的缺点在于加工难度较大，模具精加工表面质量要求高。针对这些问题，本文从表面粗糙度入手，采用球头铣刀对H13模具钢进行铣削试验，并对H13模具钢的铣削工艺参数进行优化。

在表面粗糙度预测方面，国内外学者做了大量的研究，具体可分为三个方向。首先是基于铣削理论的仿真预测，程德俊等 [1] 考虑刀具几何形状、表面倾斜角以及切削工况，提出了一种基于切削刃运动轨迹的球头铣削加工表面形貌预测模型。潘丽美等 [2] 提出了一种基于切削振动小波包分析和频谱分析的表面形貌仿真方法。其次是经验公式预测。张烘州等 [3] 建立了用于表面粗糙度预测的多元回归模型,利用响应曲面法对表面粗糙度建立等值响应曲面。石天文等 [4] 基于二阶响应曲面法建立了表面粗糙度预测模型。张宏基和葛媛媛 [5] 利用多元线性回归方法建立了铣削参数和表面粗糙度之间的数学预测模型。最后是机器学习算法预测。苏晓云等 [6] 利用粒子群优化BP神经网络建立大理石铣削加工表面粗糙度精确预测模型。吴德会 [7] 将一种基于最小二乘支持向量机的预测模型引入铣削加工领域。综合来看，机器学习算法由于在建立非线性映射关系方面拟合精度高等优势，在表面粗糙度预测中得到了更多的应用。

在铣削参数优化方面，国内外学者对于切削工艺参数的优化主要是根据设计的试验,利用算法对工艺参数进行优化。郑刚等 [8] 建立模糊预测模型，应用于优选任意铣削加工的工艺参数。Azlan M. Z等 [9] 在钛合金端面铣削时考虑了径向前角加工参数，采用遗传算法求解表面粗糙度的最优解。F. Jafarian等 [10] 以表面粗糙度、切削合力和刀具寿命为优化目标，利用神经网络和遗传算法确定最优的加工参数。吴玲等 [11] 在传统遗传算法的基础上，改进了编码方式和适应度函数，对铣削参数进行优选。上述切削参数的优化方法虽然可以进行优化求解，但往往只考虑局部最优参数，对于整体特征加工工艺参数选择具有局限性。

在目前的表面粗糙度预测研究中，铣削理论仿真预测由于铣削形貌的形成受各种因素的影响，使得这种方法受到限制；经验公式预测较为简单，但这种预测由于表面粗糙度和工艺参数之间的复杂关系导致预测的精度较低。因此本文采用神经网络预测的方法对表面粗糙度进行预测，并考虑到神经网络存在初始阈值和权重不确定的因素，利用遗传算法进行优化。同时在表面粗糙度预测模型的基础上，结合铣削材料去除率，利用多目标灰狼优化算法对工艺参数进行优化。

2. 铣削试验及分析

2.1. 试验设置

本次试验机床采用阿帕斯FGV1280数控加工中心，铣削材料为淬火后的H13模具钢，硬度为50HRC，采用神钢的两刃球头铣刀HSXB20600660，适用于模具钢等难加工材料的加工，并通过白光干涉仪测量工件的表面粗糙度。

为了研究球头铣刀铣削H13模具钢的工艺参数：主轴转速n、切削深度ap、进给速度vf、切宽ae对于表面粗糙度的影响情况，设置了四因素五水平的正交试验，各因素范围分别为：6000 < n < 14,000 r/min、0.03 < ap < 0.15 mm、1800 < vf < 3000 mm/min、0.06 < ae < 0.18 mm。

2.2. 试验结果及分析

根据正交设计展开铣削加工试验，采用面铣、湿式铣削方式，完成加工后对工件进行表面粗糙度测量，每个平面测量三次，取平均值。加工现场如图1所示。25组试验结果如表1所示。

在完成正交试验后，采用极差分析得出各因素对研究结果目标值影响的主次，极差值越大则代表该因素目标的影响程度越大，并预测更好的水平组合。对25组试验结果进行极差分析，分析结果如表2所示，并根据因素的极差值得到各水平均值图，如图2所示。

Figure 1. Experimental processing

图1. 实验加工

Table 1. Result of the orthogonal test

表1. 正交试验结果

Table 2. Range analysis results

表2. 极差分析结果

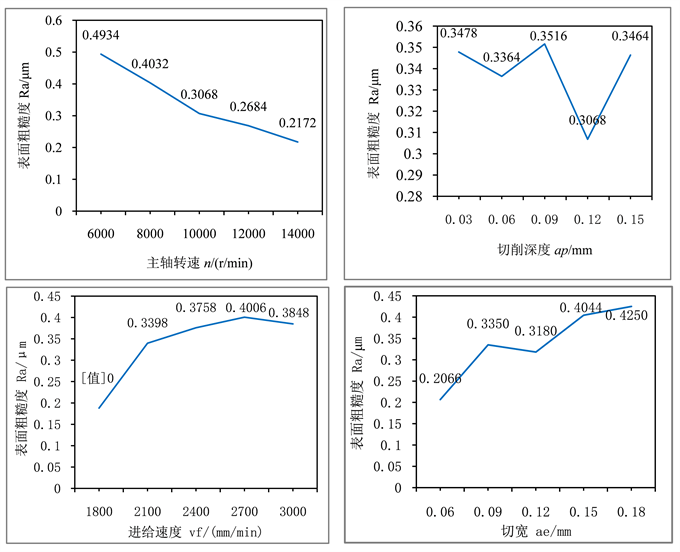
Figure 2. Mean value of each factor level

图2. 各因素水平均值

从极差分析表的结果可以看出工艺参数对于表面粗糙度的影响情况为：主轴转速 > 切宽 > 进给速度 > 切削深度；同时随着主轴转速的增大，表面粗糙度呈减小趋势，进给速度和切宽对表面粗糙度的变化总体呈上升趋势。

3. 表面粗糙度预测建模

3.1. GA-BP神经网络的表面粗糙度预测模型

作为一种多层前馈神经网络，BP神经网络从结构上看，是由一个信息的正向传播网络和一个误差的反向传播网络两个模块构成。BP神经网络的结构如图3所示，其网络结构主要由输入层、隐含层、输出层以及层与层之间的权值和阈值构成。其中，信息的正向传播过程为：来自外部的各种信息通过BP神经网络的输入层进入到隐含层进行网络运算处理，并通过输出层得到最终的处理结果；而当得到的最终结果与实际结果误差值不满足所设定的误差，则进入网络的误差方向传播，并进行网络权值的更新，直到所输出的结果能够满足所设定的误差，神经网络则迭代停止 [12] 。

BP神经网络作为一种目前比较成熟的算法，结构简单明了，但也存在着容易陷入局部最优及神经网络初始连接权值和阀值的选择对网络的预测精度及收敛速度影响很大，但又无法准确获得的问题。因此，使用遗传算法(GA)选择神经网络的初始权值和阀值。利用实验样本数据对网络进行训练，误差平方和的倒数作为BP神经网络的适应度函数 [13] 。

Figure 3. BP neural network structure

图3. BP神经网络结构

3.2. 预测模型有效性验证

在BP神经网络的设置中，通过多次学习训练，BP神经网络的结构设置为4-9-1，其中4个输入层节点(对应4个工艺参数)、1个输出层节点(表面粗糙度)、9个隐含层节点，传递函数和训练函数分别为Tansig、Levenberg Marquard，学习率为0.01，误差阈值为1e−6。遗传算法的种群规模为50，迭代次数为100代，交叉概论为0.5，变异概率为0.01。

使用正交试验的数据分别对BP神经网络和GA-BP神经网络进行训练，以预测值与真实值的相对误差e作为评价标准，如表3所示。测试集的预测结果对比，如图4所示。从测试集的预测结果可以得出，相比于BP神经网络，GA-BP神经网络的预测精度更高，平均相对误差为8.72%。

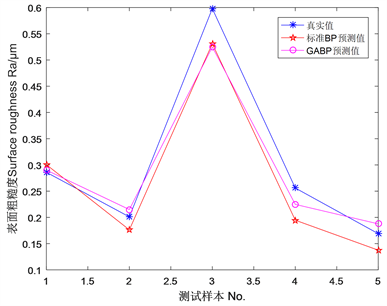
Figure 4. Comparison of predicted and true values

图4. 预测值与真实值对比

Table 3. Test set prediction comparison

表3. 测试集预测对比

4. 工艺参数优化

本节通过建立材料去除率和表面粗糙度的综合目标优化模型，对模型进行求解，并选择多特征的模具机床典型测试件铣削验证有效性。采用多目标灰狼优化算法，其中目标函数为材料去除率、表面粗糙度，优化变量为主轴转速、切削深度、进给速度、切宽。

4.1. 多目标灰狼优化算法

灰狼算法(GWO)是由Mirjalili等在2014年提出，灵感来源于灰狼的社会领导和狩猎技术，该算法的优化主要过程主要分为三步，分别为包围、追捕、攻击，将这三步分配为各等级的灰狼群来完成捕食行为，从而实现全局优化的过程 [14] [15] 。

多目标灰狼优化(Multi-Objective Grey Wolf Optimization, MOGWO)算法是在GWO的基础上提出的算法，相较于传统的启发式随机搜索算法，MOGWO所需参数更少、收敛速度更快，适用于对高维优化问题的求解。该算法将灰狼分为四个等级，优先级呈金字塔状，自上而下分别是Alpha、Beta、Delta和Omega，分别对应目标函数的最优解、次优解、第三优解和候选解。同时建立档案室，根据帕累托支配策略筛选非支配解，将其与原档案室中的解比较，选择更优解替代劣解存入档案室中。而领导者选择机制保证了能够根据目前获得的更好的解作为领导者，通过轮盘赌方法进行选择，从而引导其他搜索智能体走向搜索空间中的有希望的区域，找到近似全局最优解。迭代结束后，档案室存储的所有个体即为优化问题的最优解集 [16] 。

MOGWO算法流程如图5所示：

Figure 5. MOGWO algorithm flow

图5. MOGWO算法流程

4.2. 多目标优化模型的建立

本节建立铣削材料去除率和表面粗糙度的综合目标优化模型，对多目标、非线性优化模型进行求解。优化模型框架如图6所示。

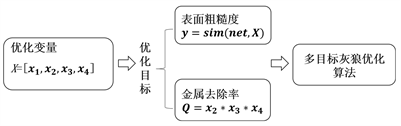
Figure 6. Multi-objective optimization modeling process

图6. 多目标优化模型流程

优化变量为 $X=\left(x_1,x_2,x_3,x_4\right)$ ， $x_1,x_2,x_3,x_4$ 分别表示主轴转速n、切削深度ap、进给速度vf、切宽ae。约束条件为6000 < n < 14,000 r/min、0.03 < ap < 0.15 mm、1800 < vf < 3000 mm/min、0.06 < ae < 0.18 mm。表面粗糙度的目标函数为第2节建立的GA-BP神经网络模型，如式(1)所示

$y=\text{sim}\left(net,X\right)$ (1)

材料去除率目标函数如式(2)所示

$ap\ast ae\ast vf$ (2)

综上所述，铣削参数多目标优化的数学模型如式(3)所示

$\begin{array}{c}\{\begin{array}{c}\min f\left(x\right)=\left\{f_1\left(x\right),f_2\left(x\right)\right\}\\ s.t{x}_{i\min }\le x_i\le x_{i\max },\left(i=1,2,3,4\right)\end{array}\end{array}$ (3)

4.3. 优化结果分析与实例验证

4.3.1. 优化结果分析

本节以工艺参数为优化变量，表面粗糙度和材料去除率为优化目标，采用Matlab语言编程，建立了多目标灰狼优化算法模型，初始种群规模设定为50，最大进化迭代数为200，非支配解集Achive个体数为50，最终得到的Pareto解集如图7所示。提取其中的部分Pareto最优解如表4所示。

Figure 7. Pareto solution set

图7. Pareto解集

Table 4. Partial Pareto solution set

表4. 部分Pareto解集

Pareto解集趋势变化表明，在前端，相比于表面粗糙度，材料去除率的变化率更大，在后端，表面粗糙度的变化率更大；主轴转速对于表面粗糙度和材料去除率的影响是显著的，且在试验的转速范围内达到上限，也验证了极差分析中主轴转速的提高对于表面粗糙度减少的影响程度；在H13钢铣削的工艺参数选择上，合理地提高主轴转速和切削深度，能够在得到较小的表面粗糙度时，达到一定的材料去除率。

4.3.2. 实例验证

本节以模具机床典型测试件为例，其具有平面、斜面、曲面等多种型面特征，不同特征反应了相应的机床加工性能，合适的工艺参数对机床性能的评估有着重要的意义，因此以测试件为例对多目标优化的工艺参数进行验证。典型测试件如图8所示，选择表4中的第4组工艺参数加工测试件中的平面，并采用正交试验中的第24组工艺参数作为对比。对优化前后平面的表面粗糙度进行测量，结果如图8所示。优化前的表面粗糙度为0.270 μm，材料去除率为25.92 mm³/min，加工时间为2242 s；优化后的表面粗糙度为0.168 μm，材料去除率为39.31 mm³/min，加工时间为1585 s。对比优化前后工艺参数的实际加工结果可以得出，优化后的工艺参数加工时实际材料去除率提高了40.1%，表面粗糙度降低了36.4%，加工时间减少了29.3%。

Figure 8. Typical test pieces for die and mold machines

图8. 模具机床典型测试件

5. 结论

模具钢高速铣削加工质量及效率受到工艺参数的影响和制约，如何选择最佳参数成为限制高精度产品的关键。本文采用GA-BP神经网络、多目标灰狼优化等算法，结合实验验证等工作，主要成果归纳如下：

1) 通过H13模具钢铣削试验，分析了球头铣刀面铣工况下主轴转速、切削深度、进给速度、切宽对表面粗糙度的影响显著程度，表现为主轴转速 > 切宽 > 进给速度 > 切削深度；

2) 利用GA-BP神经网络算法建立表面粗糙度预测模型，并与BP神经网络进行对比，GA-BP神经网络模型的预测相对误差更小，证明了预测模型的可行性；

3) 在建立的表面粗糙度预测模型的基础上，以表面粗糙度和材料去除率为优化目标，采用多目标灰狼优化算法建立了多目标工艺参数优化模型，得到了更优的工艺参数范围，并用优化前后工艺参数进行实例加工对比，验证了优化参数的有效性。

基金项目

国家自然科学基金项目资助(资助号：52175427)。