关于双树度差下界的一个例子

An Example of the Bound of Double Tree

摘要: 如果图G由两个边不交的生成树的并组成，其中E(G)=E(T₁)∪E(T₂)，且E(T₁)∩E(T₂)=∅那么称图G是双树。本文证明存在一个双树G，对于G任意一个分解f=T₁,T₂而言(T₁,T₂是生成树)，至少存在一个顶点v∈V(G)，使得▏d_T1(v)-d_T2(v)▏≥2。

Abstract: If the graph G contains two spanning trees such that the edges of spanning trees are disjoint. And E(G)=E(T₁)∪E(T₂) and E(T₁)∩E(T₂)=∅ , then we call the graph G is double tree. In this pa-per we prove that there exists a double tree graph G, for any decomposition f=T₁,T₂ (T₁,T₂ are spanning trees), there exists at least a vertex v∈V(G) such that ▏d_T1(v)-d_T2(v)▏≥2 .

1. 基本概念

我们首先给出图论中的一些相关概念。对于只有一个元素的集合$x$，我们通常用x来表示它。对于一个图G，我们用 $V\left(G\right)$ 和 $E\left(G\right)$ 来定义图G的顶点集和边集。对一些边 $e=uv\in E\left(G\right)$ ，我们称u和v与e关联或者说e连接u和v。对于某些 $X\in V$，用 ${\delta }_G\left(X\right)$ 来定义一个顶点在X中，一个顶点在 $V\left(G\right)-X$ 中的边集，用 $d_G\left(X\right)$ 来表示为 $\left|{\delta }_G\left(X\right)\right|$ 。对一些顶点 $v\in V\left(G\right)$ ，我们定义图 $G-v$ 的顶点集为 $V\left(G-v\right)=V\left(G\right)-v$ 它的边集为 $E\left(G-v\right)=E\left(G\right)-{\delta }_G\left(v\right)$ 。此外对于一条新边 $e=uv\notin E\left(G\right)$ ，其中 $u,v\in V\left(G\right)$ ，我们定义 $G+v$ 的顶点集为 $V\left(G+e\right)=V\left(G\right)$ 边集为 $E\left(G+e\right)=E\left(G\right)+e$ 。对一条新边 $e=uv\notin E\left(G\right)$ ，其中 $u\in V\left(G\right)$ 但是 $v\notin V\left(G\right)$ ，我们定义 $G+e$ 的顶点集为 $V\left(G+e\right)=V\left(G\right)+v$ 边集为 $E\left(G+e\right)=E\left(G\right)+e$ 。一个图H被叫做是另一个图G的子图如果满足 $V\left(H\right)\subseteq V\left(G\right)$ ， $E\left(H\right)\subseteq E\left(G\right)$ 。一棵树是一个连通的图且不含圈。给一个图G，一个G的子图T被称为G的支撑树如果T是一棵树且满足 $V\left(T\right)=V\left(G\right)$ 。如果一个图G包含$k$个边不交的支撑树 $T_1,\cdots ,T_k$ 且满足 $E\left(G\right)=E\left(T_1\right)\cup \cdots \cup E\left(T_k\right)$ ， $E\left(T_1\right)\cup \cdots \cup E\left(T_k\right)=\varnothing$ 我们就说G是一个k重树，并说 $T_1,\cdots ,T_k$ 是G的支撑树分解。此外我们把2重树叫做双树。如果图G是一个双树，在图G上存在一个分界 $f=\left(T_1,T_2\right)$ ，其中 $T_1,T_2$ 都是生成树并且 $E\left(T_1\right)\cup E\left(T_2\right)=\varnothing$ 。那么称这个分解f为图G的双树分解。我们可以得到双树有如下的结论。

命题1：每个双树满足 $\left|E\left(G\right)\right|=2\left|V\left(G\right)\right|-2$ 。

下面的命题是我们所熟知的支撑树的交换操作。

命题2 [1] ：令G是一个双树， $\left(T_1,T_2\right)$ 是G的支撑树分解。则存在一个函数 $\sigma :E\left(T_1\right)\to E\left(T_2\right)$ 使得 $\left(T_1-e+\sigma \left(e\right),T_2-\sigma \left(e\right)+e\right)$ 也是G的一个支撑树分解。

我们把如上的命题中的函数叫做从 $T_1$ 到 $T_2$ 的树交换函数。这个在文献 [1] 中已经被证明。

2022年8月，学者Florian Horsch在文献 [2] 证明了对每个包含两个边不交的支撑树的图G，我们可以选择图G中的一个分解 $\left(T_1,T_2\right)$ 使得对于任意的顶点 $v\in V\left(G\right)$ 都有 $\left|d_{T_1}\left(v\right)-d_{T_2}\left(V\right)\right|\le 5$ 。这给出了如果图G可以分解成两个支撑树，那么这两个支撑树的顶点度差的上界是5。在这个文献中学者证明了树交换函数的性质。

命题3：令G是一个双树， $\left(T_1,T_2\right)$ 是G的一个支撑树分解，且 $v\in V\left(G\right)$ 其中x关联于 $T_1$ 中的唯一的边。则对任何树交换函数 $\sigma :E\left(T_1\right)\to E\left(T_2\right)$ ，我们都有 $\sigma \left(e\right)\in {\delta }_G\left(x\right)$ 。

证明：因为 $T_1-e+\sigma \left(e\right)$ 是一个G的支撑树，存在至少一条边 $f\in \left(E\left(T_1\right)-e+\sigma \left(e\right)\right)\cap {\delta }_G\left(x\right)$ 。因为 $\left(E\left(T_1\right)-e\right)\cap {\delta }_G\left(x\right)=\varnothing$ ，我们有 $f=\sigma \left(e\right)$ 。

在1961年，在文献 [3] 中学者Nash-Williams以及在文献 [4] 中学者Tutte独立地证明了一个基本定理，该定理表征了包含固定数量的边不相交生成树的图的特征。从那以后，已经发现了几个扩展该定理的结果。例如，虽然它没有扩展到一般的无限图，但它已被学者Lehner [5] 和Stein [6] 推广到某些类的无限图。学者Chuzoy，Parter和Tan [3] 已经考虑了有界直径的生成树。此外，满足某种平衡条件的生成树，即删除指定的顶点不应留下包含在单个连接组件中所有顶点的图，Bang-Jensen，Havet和Yeo [7] 以及Bessy等人已经进行了相关研究。在这篇文章中我们通过一个例子从而得到存在一个双树G，对于它的任何一个分解 $\left(T_1,T_2\right)$ ，而言满足存在至少一个顶点v使得 $\left|d_{T_1}\left(v\right)-d_{T_2}\left(v\right)\right|\ge 2$ 。

2. 主要定理

本文主要证明的定理如下：存在一个双树G，对于任何G的任何一个双树分解 $\left(T_1,T_2\right)$ 而言，存在一个顶点 $v\in V\left(G\right)$ ，使得 $\left|d_{T_1}\left(v\right)-d_{T_2}\left(v\right)\right|\ge 2$ 。

3. 主要定理证明

接下来我们给出一个例子“见图1”所示，通过对于这个例子的所有分解进行讨论，从而得到定理1的证明。

Figure 1. Example G

图1. 例G

引理1：对于G的任何一个分解 $\left(T_1,T_2\right)$ ，如果 $e,f$ 是G上的重边，那么 $e,f$ 不可能位于同一棵树 $T_i$ ，其中 $i=1,2$ 。

证明：我们利用反证法进行证明，不妨假 $e,f$ 都在同一棵树 $T_1$ 上，那么对于图G的任何一个分解，我们都会得到 $T_1$ 上存在一个圈，矛盾于 $T_1$ 是一棵树。

我们对上述所给出的例子进行分析，首先收缩顶点 $x_1,x_2,x_3$ 为一个顶点X，收缩顶点 $y_1,y_2,y_3$ 为一个顶点Y，则我们得到了一个新的图 $G^{\prime }$ ，“见图2”中展示它的顶点集为 $V\left(G^{\prime }\right)=\left\{X,Y,Z\right\}$ 。

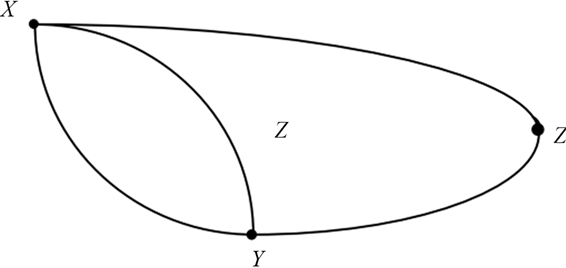
Figure 2. Edge contracted of the graph G

图2. 图G 的收缩图

事实1：图G是一棵双树，则通过收缩操作之后得到的图 $G^{\prime }$ 也是一棵双树。

证明：a如图所示不妨假设 $E\left(G^{\prime }\right)=\left\{e_1,e_2,e_3,e_4\right\}$ ，其中 $e_1=XY,e_2=XY,e_3=XZ,e_4=YZ$ ，根据引理1可得 $e_1,e_2$ 不可能位于同一棵树 $T_i$ 中，不妨假设 $e_1\in T_1$ 以及 $e_2\in T_2$ 。由于Z在 $G^{\prime }$ 上只有二度点，因此 $e_3,e_4$ 在不同的树上，那么在新图 $G^{\prime }$ 中我们得到了新的分解 $\left(T_1,T_2\right)$ ，从而证明了这个事实。

事实2：图G中包含一个三角形不妨假设这三条边分别为 $e_1,e_2,e_3$ ，那么这三条边都不会属于同一个 $T_i$ 。

证明：利用反证法，不妨假设 $e_1,e_2,e_3$ 都在同一棵树 $T_1$ 上，那么对于图G的任何一个分解，我们都会得到 $T_1$ 上存在一个圈，矛盾于 $T_1$ 是一棵树。

推论1：图G中包含一个三角形，那么这三条边中至少有一条边属于 $T_i$ 其中 $i=1,2$ ，另外两条边属于 $T_{3-i}$ 。

下面我们对于上述给出的例子，通过对这个例子的所有的分解进行讨论从而证明对于双树G，对于任何G的两个边不相交生成树 $\left(T_1,T_2\right)$ 而言，存在一个顶点 $v\in V\left(G\right)$ ，使得 $\left|d_{T_1}\left(v\right)-d_{T_2}\left(v\right)\right|\ge 2$ 。下面我们都是基于图 $G=\left(T_1,T_2\right)$ 进行讨论。

下面我们对图G的边集进行讨论，不妨假设 $e_1,f_1$ 是关联 $x_2$ 和 $x_3$ 的两条重边， $e_3,f_3$ 是关联 $y_2$ 和 $y_3$ 的两条重边， $e_2=x_3{y}_3$ ， $f_2=x_1{y}_1$ 。与Z点相关联的边集我们在下面的Case中进行具体的分析讨论。接下来根据上述所谈到的事实和推论我们对它们的边集进行划分，因为 $e_1,f_1$ 以及 $e_3,f_3$ 是两对重边，因此 $e_1,f_1$ 属于不同的 $T_i$ ， $e_3,f_3$ 属于不同的 $T_i$ 。为了不失一般性我们不妨假设 $e_1,e_3\in T_1$ ， $f_1,f_3\in T_2$ 。由引理1可得 $e_2,f_2$ 位于不同的树上。接下来我们分情况讨论。

Case A.如果 $e_2\in T_1,f_2\in T_2$

Case A.1因为 $G\left[x_1,x_2,x_3\right]$ 中包含两个三角形，由事实2可得 $x_1{x}_2,x_1{x}_3$ 不可能同时位于同一棵树上。如果 $x_1{x}_3\in T_1$ ，那么 $x_1{x}_2\in T_2$ 。我们发现对于顶点 $x_3$ 来说有， $\left|d_{T_1}\left(x_3\right)-d_{T_2}\left(x_3\right)\right|=2$ 。如果 $x_1{x}_2\in T_1$ ，那么

Figure 3. The Case B.2

图3. 情况B.2

$x_1{x}_3\in T_2$ 。我们来讨论 $G\left[y_1,y_2,y_3\right]$ ，因为 $G\left[y_1,y_2,y_3\right]$ 中包含两个三角形，由事实2可得 $y_1{y}_2,y_1{x}_3$ 不可能同时位于同一棵树上。如果 $y_1{y}_3\in T_1$ ，那么 $y_1{y}_2\in T_2$ 。我们发现对于顶点 $y_3$ 来说有度差的绝对值为2。

Case A.2

如果 $y_1{y}_3\in T_2$ ，那么 $y_1{y}_2\in T_1$ ，这时候我们发现对于 $x_2,y_2$ 来说有且 $d_{T_1}\left(y_2\right)-d_{T_2}\left(y_2\right)=1$ 。又因为 $z\in V\left(G\right)$ ，且 $d_G\left(z\right)=2$ ， $T_1,T_2$ 是G的支撑树，因此 $d_{T_1}\left(z\right)=d_{T_2}\left(z\right)=1$ 。我们知道 $z{x}_2,z{y}_2$ 不可能属于同一棵树，则存在 $x_2$ 或者 $y_2$ 中至少一个点有 $\left|d_{T_1}\left(x_2\right)-d_{T_2}\left(x_2\right)\right|=2$ 或者 $\left|d_{T_1}\left(y_2\right)-d_{T_2}\left(y_2\right)\right|=2$ 。

Case B.否则 $e_2\in T_2,f_2\in T_1$ 。

Case B.1因为 $G\left[x_1,x_2,x_3\right]$ 中包含两个三角形，由事实2可得 $x_1{x}_2,x_1{x}_3$ 不可能同时位于同一棵树上。如果 $x_1{x}_3\in T_2$ ，那么 $x_1{x}_2\in T_1$ 。我们发现对于顶点 $x_3$ 来说有， $\left|d_{T_1}\left(x_3\right)-d_{T_2}\left(x_3\right)\right|=2$ 。

Case B.2如果 $x_1{x}_2\in T_2$ ，那么 $x_1{x}_3\in T_1$ 。我们来讨论 $G\left[y_1,y_2,y_3\right]$ ，因为 $G\left[y_1,y_2,y_3\right]$ 中包含两个三角形，由事实2可得 $y_1{y}_2,y_1{x}_3$ 不可能同时位于同一棵树上。如果 $y_1{y}_3\in T_2$ ，那么 $y_1{y}_2\in T_1$ 。我们发现对于顶点 $y_3$ 来说有， $\left|d_{T_1}\left(y_3\right)-d_{T_2}\left(y_3\right)\right|=2$ 。如果 $y_1{y}_3\in T_1$ ，那么 $y_1{y}_2\in T_2$ ，这时候我们发现对于 $x_2,y_2$ 来说有 $d_{T_2}\left(x_2\right)-d_{T_1}\left(x_2\right)=1$ 且 $d_{T_2}\left(y_2\right)-d_{T_1}\left(y_2\right)=1$ 。又因为 $z\in V\left(G\right)$ ，且 $d_G\left(z\right)=2$ ， $T_1,T_2$ 是G的支撑树，因此 $d_{T_1}\left(z\right)=d_{T_2}\left(z\right)=1$ 。我们知道 $z{x}_2,z{y}_2$ 不可能属于同一棵树，则存在 $x_2$ 或者 $y_2$ 中至少一个点有 $\left|d_{T_1}\left(x_2\right)-d_{T_2}\left(x_2\right)\right|=2$ 或者 $\left|d_{T_1}\left(y_2\right)-d_{T_2}\left(y_2\right)\right|=2$ 。“见图3”片所示。

4. 结语

森林分解在图论研究中占据了极大的比重，文献 [5] 中已经证明了双树分解的度差上界是5，那么对于双树分解度差的下界就是一个非常值得研究的问题，通过对度差上下界的讨论从而帮助我们的得到相对平衡的双树分解。我们目前已经找到一种双树，使得对于任意的分解都会存在一个顶点的度差大于等于2，那对于任意的图都有这样的问题这也是值得进一步探讨的问题。