带资源项的随机尺度结构系统数值收敛性分析

doi:10.12677/AAM.2023.125233

期刊菜单

带资源项的随机尺度结构系统数值收敛性分析
Numerical Convergence Analysis of Stochastic Size-Structured Models with Resource Term

DOI: 10.12677/AAM.2023.125233, PDF, HTML, XML, 下载: 120 浏览: 172 国家自然科学基金支持
作者: 卫烁遥, 李心^*：燕山大学理学院，河北秦皇岛
关键词: Markovian转换；随机种群；尺度结构；半隐式欧拉；收敛性；Markovian Transformation； Random Population； Scale Structure； Semi-Implicit Euler； Convergence

摘要: 种群研究作为生物研究的重要组成部分之一，在生物发展进程中起着至关重要的作用。文章考虑了一类带有特殊资源项和随机因素的尺度结构系统数值解的收敛性问题。首先，利用半隐式欧拉数值方法，构造离散模型的数值解；随后，在一定的假设条件下，利用Itô引理，讨论了该系统数值解的依均方收敛性；最后，根据离散系统的特点对带有尺度结构的随机种群模型进行了数值模拟，同时验证数值方法的可靠性。

Abstract: Population research plays an important role in biological research as an important part of biological research. The convergence of numerical solutions for a class of scale-structured systems with special resource terms and random factors is considered in this paper. First, the numerical solutions of dis-crete models are constructed by using semi-implicit Euler numerical methods. Then, under certain assumptions, the mean-square convergence of the numerical solution of the system is discussed using the Itô lemma. Finally, the stochastic population model with size-structure is simulated nu-merically according to the characteristics of the discrete system, and the reliability of the numerical method is verified.

文章引用：卫烁遥, 李心. 带资源项的随机尺度结构系统数值收敛性分析[J]. 应用数学进展, 2023, 12(5): 2288-2302. https://doi.org/10.12677/AAM.2023.125233

1. 引言

近年来，随机分析发展迅速，带有随机项的微分方程已被广泛的应用于社会中的各个领域 [1] [2] [3] 。种群问题自提出以来就备受关注。种群问题的研究对描述生物的发展趋势有着重要的指导意义。种群在发展的过程中会受到一些随机因素的影响，因此在研究种群问题时考虑随机因素的影响会使研究更加全面。

对于带有随机因素年龄结构种群的研究，已经取得了一定的进展。Zhang和Han [4] 提出一种数值迭代格式，用来求得随机年龄种群的数值解，并证明了数值解的收敛性。Li等 [5] 证明了在局部Lipschitz条件下，带Markovian转换年龄依赖随机种群模型数值解的依均方收敛性。同时，马东娟和张启敏 [6] 提出带有Poisson跳的随机种群扩散系统，利用半隐式欧拉方法获得的解收敛于系统的真实解。Li等 [7] 研究了污染环境中具有Markovian转换的随机年龄结构种群模型，利用截断EM方法，建立了数值逼近在q阶矩下的强收敛准则。此外，Shi [8] 阐述了在给定的数值边界条件下，利用隐式欧拉方法将随机年龄结构人口模型完全离散化，并对其所得的数值解进行了收敛分析。

然而，在生物种群实际问题的研究过程中，仅考虑年龄因素对生物种群的影响还不够全面。因此，带有尺度结构的生物种群模型应运而生。尺度结构是指种群中受自身影响的因素，例如生物的质量、长度、年龄、宽度等。生物的个体尺度对生物个体的繁殖能力、新陈代谢能力、摄食率、死亡率都有着很大程度的影响。目前，对于带有尺度结构模型的研究主要有：Itô等 [9] 提出一种算法用于计算尺度结构模型的解。Ackleh和Itô [10] 考虑“完全非线性”尺度结构种群模型，利用隐式有限差分格式来逼近此方程的解，并且验证了该模型解的收敛性。同时，Abia等 [11] 综合概括了求解尺度结构模型的数值方法，并比较了这些方法在准确性、效率、通用性等方面的优劣性。Angulo和López-Marcos [12] 利用二阶特征方法来获得尺度结构种群模型的数值解。此外，刘炎 [13] 进一步研究了带有资源项制约的尺度结构种群平衡解的稳定性，利用算子半群等理论将非线性化系统线性化，并最终给出平衡解的稳定条件。Liu和He [14] 对带有资源项的尺度结构模型也进行了讨论，利用算子半群、特征方程的方法得到了系统的平衡解。随后，袁志宏 [15] 考虑了具有尺度结构种群动力系统的定性行为，应用微分方程的比较原理, 证明了该系统解的存在唯一性。刘荣 [16] 考虑了几类具有尺度结构的种群动力学系统，利用泛函分析、微–积分方程等理论，分析系统的动力学行为。

综上，关于随机年龄结构和确定性尺度结构的研究已经相对成熟。但就目前而言，几乎没有关于随机尺度结构模型的研究。基于自然界中随机性因素对尺度种群有着不可忽略影响的现实需要，本文充分考虑了随机因素对尺度结构种群带来的影响，克服了存在随机因素的系统解难以直接解出的困难，提出了利用数值方法将模型离散化求得数值解的方法，根据Itô引理，在假设条件下得到了模型数值解的收敛性结果。

2. 模型描述及预备知识

2.1. 模型描述

由生物学的背景可知，生物的生存需要水、空气、食物、领地等，其统称为资源。生物的出生率、死亡率、增长率受资源的影响。基于以上阐述，建立了受资源影响的随机尺度结构种群模型：

${\begin{cases} \frac{\partial P (s, t)}{\partial t} + \frac{\partial P (s, t) g (s, R (t))}{\partial s} = - μ (s, R (t)) P (s, t) + f (r (t), P) + z (r (t), P) \frac{d W (t)}{d t} \\ P (0, t) = \int_{0}^{M} β (s, R (t)) P (s, t) d s \\ \frac{d R (t)}{d t} = h (R (t)) - \int_{0}^{M} ω (s, R (t), p (t, s)) d s \\ R (0) = R_{0} \\ P (s, t) = \int_{0}^{M} p (s, t) d s \\ P (s, 0) = P_{0} (s) \end{cases}$ (1)

其中 $t \in (0, T), s \in (0, M)$ ， $P (s, t)$ 表示尺度为s，时间为t时种群的密度； $R (t)$ 表示在时刻t资源的总量； $g (s, R (t)), μ (s, R (t)), β (s, R (t))$ 分别表示依赖于资源的种群内部的增长率、出生率、死亡率；

$h (R (t)) = r R (1 - \frac{R (t)}{K}), r > 0$ 满足logistic增长条件，表示不考虑种群内部自身资源消耗下资源的消耗量；

$r (t)$ 为可数状态的右连续Markov链； $ω (s, R (t), p (t, s))$ 表示种群内部资源的消耗量； $f (r (t), p)$ 表示种群系统外在环境的影响； $z (r (t), p)$ 表示种群的扩散系数。

2.2. 预备知识

令 $V = H^{1} ([0, M]) \equiv {φ | φ \in L^{2} ([0, M]), \frac{\partial φ}{\partial s} \in L^{2} ([0, M])}$ ，其中 $\frac{\partial φ}{\partial s}$ 是广义偏导数。V是Sobolev空间，

$H = L^{2} ([0, M])$ ， $V \to H \equiv H^{'} \to V^{'}, V^{'} = H ([0, M])$ 是V的对偶空间。在 $V, H, V^{'}$ 上的范数分别为 $‖ \cdot ‖, | \cdot |, {‖ \cdot ‖}_{*}$ 。记 $(\cdot, \cdot)$ 表示H空间中的标量内积， $〈 \cdot, \cdot 〉$ 为V与 $V^{'}$ 之间的对偶内积。记K为可分的Hilbert空间。对于 $B \in L (K, H)$ ，其中 $L (K, H)$ 表示从K到H的所有有界线性算子构成的空间。用 ${‖ B ‖}_{2}$ 来表示Hilbert-Schmidt范数， ${‖ B ‖}_{2} = t r (B W B^{T})$ 。

记 $(Ω, F, P)$ 是一个完备的概率空间，其中 ${F_{t}}_{t > 0}$ 流满足一般条件，即递增、右连续，且包含所有的零测度集。 $r (t), t \geq 0$ 是完备概率空间上右连续的Markov链，在有限状态空间 $S = {1, 2, \dots, N}$ 取值，其生成元 $Γ = {(r_{i j})}_{N \times N}$ 如下：

$P {r (t + Δ t) = j | r (t) = i} = {\begin{cases} r_{i j} Δ t + o (Δ t), i \neq j, \\ 1 + r_{i j} Δ t + o (Δ t), i = j, \end{cases}$

其中 $Δ t > 0$ ， $r_{i j}$ 为从i到j的转移率，当 $i \neq j$ 时， $r_{i j} = - \sum_{i \neq j} r_{i j}$ 。

在本文中， $W_{t}$ 为定义在完备概率空间 $(Ω, F, P)$ 上，具有协方差增量W，且取值在空间K上的标准Brown运动。令 $C = C ([0, M]; H)$ ，C是指从 $[0, M]$ 到H的所有的连续函数所组成的空间，其中的范数定义为：

${‖ φ ‖}_{C} = \sup_{0 \leq s \leq M} | φ (s) |, L_{V}^{P} = L^{P} ([0, M]; V), L_{H}^{P} = L^{P} ([0, M]; H) .$

考虑以下带有资源项的随机尺度结构模型半隐式欧拉方法的构造过程：

$\begin{matrix} \partial_{t} P (s, t) = [- \frac{\partial P (s, t)}{\partial s} g (s, R (t)) - P (s, t) \frac{\partial g (s, R (t))}{\partial s}] d t \\ - μ (s, R (t)) P (s, t) d t + f (r (t), P) d t + Z (r (t), P) d w_{t} . \end{matrix}$ (2)

将方程(2)用积分的形式表示：

$\begin{array}{l} P (s, t) = P (s, 0) + \int_{0}^{t} [- \frac{\partial P (s, t)}{\partial s} g (s, R (t)) - P (s, t) \frac{\partial g (s, R (t))}{\partial s}] d t \\ + \int_{0}^{t} (- μ (s, R (t)) P (s, t)) + f (r (t), P) d t + \int_{0}^{t} Z (r (t), P) d w_{t} . \end{array}$ (3)

令 $Δ t = \frac{T}{N} ≪ 1, θ \in [0, 1]$ ，给出方程(3)在时间 $t \in {0, Δ t, 2 Δ t, \dots, N Δ t = T}$ 上定义的半隐式欧拉迭代格式：

$\begin{array}{l} V_{t}^{n + 1} = V_{t}^{n} + (1 - θ) [- \frac{\partial V_{t}^{n +1}}{\partial s} \cdot g (s, R (t)) - V_{t}^{n} \frac{\partial g (s, R (t))}{\partial s} - μ (s, R (t)) V_{t}^{n} + f (r_{n}^{Δ t}, V_{t}^{n})] Δ t \\ + θ [- \frac{\partial V_{t}^{n + 1}}{\partial s} \cdot g (s, R (t)) - V_{t}^{n + 1} \frac{\partial g (s, R (t))}{\partial s} - μ (s, R (t)) V_{t}^{n + 1} + f (r_{n}^{Δ t}, V_{t}^{n + 1})] Δ t + z (r_{n}^{Δ t}, V_{t}^{n}) Δ W_{n}, \end{array}$ (4)

其中

$Δ W_{n} = W (t_{n + 1}) - W (t_{n}) \sim N (0, Δ t), V_{t}^{0} = V (t, 0) = P (t, 0), V^{n} (t, 0) = \int_{0}^{M} β (s, R (t)) V_{t}^{n} d s,$

$V_{t}^{n + 1}$ 是 $P (s, t_{n + 1})$ $(n = 0, 1, 2, 3, \dots, N - 1)$ 的逼近值，利用阶梯函数将离散的时间变量用连续的时间变量定义。给定步长函数

$H_{1} (t) = H_{1} (s, t) = \sum_{n = 0}^{N - 1} V_{t}^{n} I_{[n Δ t, (n + 1) Δ t]}, H_{2} (t) = H_{2} (s, t) = \sum_{n = 0}^{N - 1} V_{t}^{n + 1} I_{[n Δ t, (n + 1) Δ t]},$

其中 $\bar{r} (t) = \sum_{n = 0}^{N - 1} r_{n}^{Δ t} I_{[n Δ t, (n + 1) Δ t]}$ .

为了后续证明方便，假设：

1) $f (i, 0) = 0, z (i, 0) = 0, i \in X$ ；

2) 存在一个大于零的常数 $K_{i}$ ，对任意的 $x, y \in C, i \in X$ ，使得

$| f (i, x) - f (i, y) | \lor {‖ z (i, x) - z (i, y) ‖}_{2} \leq K_{i} {‖ x - y ‖}_{C}, a . e . t;$

3) $μ (s, R (t)), g (s, R (t)), β (s, R (t))$ 在 $\bar{Q} = Q + \partial Q$ 上是连续的，且存在正常数 $μ_{0}, α, β, g_{1}, g_{2}, g_{3}$ ，使得

$0 \leq μ_{0} \leq μ (s, R (t)) \leq α < \infty, 0 \leq g_{1} \leq g (s, R (t)) \leq g_{2} < \infty, 0 \leq β (s, R (t)) \leq β < \infty, | \frac{\partial g (s, R (t))}{\partial s} | \leq g_{3} .$

3. 相关引理及证明

将离散后的方程(4)对时间进行积分可得

$\begin{matrix} V_{t} = V_{0} + \int_{0}^{t} (1 - θ) [- \frac{\partial V_{x}}{\partial s} g (s, R (x)) - H_{1} (x) \frac{\partial g (s, R (x))}{\partial s} - μ (s, R (x)) H_{1} (x) + f (\bar{r} (t), H_{1} (x))] d x \\ + \int_{0}^{t} θ [- \frac{\partial V_{x}}{\partial s} \cdot g (s, R (x)) - H_{2} (x) \frac{\partial g (s, R (x))}{\partial s} - μ (s, R (x)) H_{2} (x) + f (\bar{r} (t)), H_{2} (x)] d x \\ + z (\bar{r} (t), H_{1} (x)) d W_{x} . \end{matrix}$ (5)

引理1 假设条件(1)~(3)成立，则存在正常数 $C_{0}, C_{1}, p \geq 2$ ，使得

$E [\sup_{0 \leq t \leq T} {| V_{t} |}^{p}] \leq C_{0},$ (6)

$E [\sup_{0 \leq t \leq T} {| P_{t} |}^{p}] \leq C_{1} .$ (7)

证明：对 ${| V_{t} |}^{p}$ 应用Itô公式

$\begin{array}{l} {| V_{t} |}^{p} = {| V_{0} |}^{p} + \int_{0}^{t} p {| V_{x} |}^{p - 2} 〈 - \frac{\partial V_{x}}{\partial s} g (s, R (t)), V_{x} 〉 d x \\ + \int_{0}^{t} p {| V_{x} |}^{p - 2} (- \frac{\partial g (s, R (t))}{\partial s} [(1 - θ) H_{1} (x) + θ H_{2} (x)], V_{x}) d x \\ + \int_{0}^{t} p {| V_{x} |}^{p - 2} (- μ (s, R (t) [(1 - θ) H_{1} (x) + θ H_{2} (x)], V_{x}) d x \\ + \int_{0}^{t} p {| V_{x} |}^{p - 2} ([(1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{1} (x))], V_{x}) d x \end{array}$

$\begin{array}{l} + \int_{0}^{t} p {| V_{x} |}^{p - 2} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}) + \int_{0}^{t} \frac{p (p - 2)}{2} {| V_{x} |}^{p - 4} {‖ (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}) ‖}_{2}^{2} \\ + \int_{0}^{t} \frac{p}{2} {| V_{x} |}^{p - 2} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x \\ \leq {| V_{0} |}^{p} + \int_{0}^{t} p {| V_{x} |}^{p - 2} 〈 - \frac{\partial V_{x}}{\partial s} g (s, R (t)), V_{x} 〉 d x + g_{3} \int_{0}^{t} p {| V_{x} |}^{p - 2} ([(1 - θ) H_{1} (x) + θ H_{2} (x)], V_{x}) d x \\ - μ_{0} \int_{0}^{t} p {| V_{x} |}^{p - 2} ([(1 - θ) H_{1} (x) + θ H_{2} (x)], V_{x}) d x \end{array}$

$\begin{array}{l} + \int_{0}^{t} p {| V_{x} |}^{p - 2} ([(1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{1} (x))], V_{x}) d x \\ + \int_{0}^{t} p {| V_{x} |}^{p - 2} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}) + \int_{0}^{t} \frac{p (p - 2)}{2} {| V_{x} |}^{p - 4} {‖ (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}) ‖}_{2}^{2} \\ + \int_{0}^{t} \frac{p}{2} {| V_{x} |}^{p - 2} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x . \end{array}$

由假设条件(2)和 $V^{n} (t, 0) = \int_{0}^{M} β (s, R (t)) V_{t}^{n} d s$ 可知

$\begin{array}{l} 〈 - \frac{\partial V_{x}}{\partial s} g (s, R (x)), V_{x} 〉 = - \int_{0}^{M} V_{x} \cdot g (s, R (x)) d V_{x} \leq - g_{1} \int_{0}^{M} V_{x} d V_{x} \leq g_{1} (\frac{V^{2} (x, 0)}{2} - \frac{V^{2} (x, M)}{2}) \\ \leq g_{1} \frac{V^{2} (x, 0)}{2} \leq \frac{1}{4} g_{1} \int_{0}^{M} β^{2} (s, R (t)) d s \int_{0}^{M} V_{x}^{2} d s \leq \frac{1}{4} g_{1} M^{2} β^{2} {| V_{x} |}^{2}, \end{array}$

由假设条件(3)得

$| (1 - θ) H_{1} (x) + θ H_{2} (x) | \leq | H_{1} (x) | + | H_{2} (x) | \leq 2 K_{i} {‖ V_{x} ‖}_{C}$

和

$| (1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{2} (x)) | \leq | f (\bar{r} (x), H_{1} (x)) | + | f (\bar{r} (x), H_{2} (x)) | \leq 2 K_{i} {‖ V_{x} ‖}_{C} .$

则

$\begin{array}{l} {| V_{t} |}^{p} \leq {| V_{0} |}^{p} + \frac{1}{2} g_{1} M^{2} β^{2} \int_{0}^{t} p {| V_{x} |}^{p} d x + 2 K_{i} (g_{3} + μ_{0}) \int_{0}^{t} p {| V_{x} |}^{p - 1} {‖ V_{x} ‖}_{C} d x \\ + 2 K_{i} \int_{0}^{t} p {| V_{x} |}^{p - 1} {‖ V_{x} ‖}_{C} d x + \int_{0}^{t} p {| V_{x} |}^{p - 2} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}) \\ + \int_{0}^{t} \frac{p (p - 2)}{2} {| V_{x} |}^{p - 2} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x \\ + \int_{0}^{t} \frac{p}{2} {| V_{x} |}^{p - 2} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x, \end{array}$

对任意 $t_{1} \in [0, T]$ 有

$\begin{array}{l} E [\sup_{0 \leq t \leq t_{1}} {| V_{x} |}^{p}] \leq E {| V_{0} |}^{p} + \frac{1}{2} (p g_{1} M^{2} β^{2}) E [\sup_{0 \leq t \leq t_{1}} \int_{0}^{t} {| V_{x} |}^{p} d x] + 2 p K_{i} (g_{3} + μ_{0} + 1) \\ E [\sup_{0 \leq t \leq t_{1}} \int_{0}^{t} {| V_{x} |}^{p - 1} {‖ V_{x} ‖}_{C} d x] + E [\sup_{0 \leq t \leq t_{1}} \int_{0}^{t} p {| V_{x} |}^{p - 2} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x})] \\ + E [\sup_{0 \leq t \leq t_{1}} (\int_{0}^{t} \frac{p (p - 1)}{2} {| V_{x} |}^{p - 2} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2}) d W_{x}] \\ \leq E {| V_{0} |}^{p} + [\frac{1}{4} (p g_{1} M^{2} β^{2}) + 2 p K_{i} (g_{3} + μ_{0} + 1) + \frac{p (p - 1)}{2} K_{i}] \int_{0}^{t} E (\sup_{0 \leq t \leq t_{1}} {| V_{x} |}^{p}) d x \\ + E [\sup_{0 \leq t \leq t_{1}} \int_{0}^{t} p {| V_{x} |}^{p - 2} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x})] . \end{array}$

存在一个正常数K₁，利用Burkholder-Davis-Gundy不等式可得

$\begin{array}{l} E [\sup_{0 \leq t \leq t_{1}} \int_{0}^{t} {| V_{x} |}^{p - 2} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x})] \\ = E [\sup_{0 \leq t \leq t_{1}} \int_{0}^{t} ({| V_{x} |}^{\frac{p - 2}{2}} V_{x}, {| V_{x} |}^{\frac{p - 2}{2}} z (\bar{r} (x), H_{1} (x)) d W_{x})] \\ \leq 3 E [\sup_{0 \leq t \leq t_{1}} {| V_{x} |}^{\frac{p}{2}} {\int_{0}^{t} ({| V_{x} |}^{p - 2} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x)}^{\frac{1}{2}}] \\ \leq \frac{1}{2 p} E [\sup_{0 \leq t \leq t_{1}} {| V_{x} |}^{p}] + K_{1} K_{i} \int_{0}^{t} E [\sup {| V_{x} |}^{p - 2} {‖ V_{x} ‖}_{C}^{2}] d x . \end{array}$

则

$E [\sup_{0 \leq t \leq t_{1}} {| V_{t} |}^{p}] \leq 2 E {| V_{0} |}^{p} + [\frac{1}{2} p g_{1} M^{2} β^{2} + 4 p K_{i} (g_{2} + μ_{0} + 1) + p (p - 1) K_{i} + 2 p K_{1} K_{i}^{2}] \int_{0}^{t} E [\sup_{0 \leq t \leq t_{1}} {| V_{x} |}^{p}] d x .$

根据Gronwall不等式有

$\begin{array}{l} E [\sup_{0 \leq t \leq T} {| V_{t} |}^{p}] \leq 2 E {| V_{0} |}^{p} e^{[\frac{1}{2} p g_{1} M^{2} β^{2} + 4 p K_{i} (g_{2} + μ_{0} + 1) + p (p - 1) K_{i} + 2 p K_{1} K_{i}^{2}] t} \\ \leq 2 E {| V_{0} |}^{p} e^{[\frac{1}{2} p g_{1} M^{2} β^{2} + 4 p K_{i} (g_{2} + μ_{0} + 1) + p (p - 1) K_{i} + 2 p K_{1} K_{i}^{2}] T}, \end{array}$

其中 $C_{1} = 2 E {| V_{0} |}^{p} e^{[\frac{1}{2} p g_{1} M^{2} β^{2} + 4 p K_{i} (g_{2} + μ_{0} + 1) + p (p - 1) K_{i} + 2 p K_{1} K_{i}^{2}] T} .$

综上所述 $E [\sup_{0 \leq t \leq T} {| V_{t} |}^{p}] \leq C_{1}$ 。(6)与(7)同理可证，引理1得证.

引理2 假设条件(1)~(3)成立，且满足 $E {| \frac{\partial V_{x}}{\partial s} |}^{2} < \infty$ ，则存在正常数C₂，C₃，使得

$E [\sup_{0 \leq t \leq T} {| V_{t} - H_{1} (x) |}^{2}] \leq C_{2} Δ t .$

证明：对 $\forall t \in [0, T]$ ，存在正整数K，使得 $t \in [n Δ t, (n + 1) Δ t]$ 时有

$\begin{array}{l} V_{t} - H_{1} (t) = V_{t} - V_{t}^{k} = - \int_{n Δ t}^{t} \frac{\partial V_{x}}{\partial s} g (s, R (x)) d x - \int_{n Δ t}^{t} \frac{\partial g (s, R (x))}{\partial s} ((1 - θ) H_{1} (x) + θ H_{2} (x)) d x \\ - \int_{n Δ t}^{t} μ (s, R (x)) ((1 - θ) H_{1} (x) + θ H_{2} (x)) d x \\ + \int_{n Δ t}^{t} (1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{2} (x)) d x \\ + \int_{n Δ t}^{t} z (\bar{r} (x), H_{1} (x)) d W_{x}, \end{array}$

已知 ${| a + b + c + d + e |}^{2} \leq 5 {| a |}^{2} + 5 {| b |}^{2} + 5 {| c |}^{2} + 5 {| d |}^{2} + 5 {| e |}^{2}$ ，

$\begin{array}{l} {| V_{t} - H_{1} (t) |}^{2} \leq 5 {| \int_{n Δ t}^{t} \frac{\partial V_{x}}{\partial s} g (s, R (x)) d x |}^{2} + 5 {| \int_{n Δ t}^{t} \frac{\partial g (s, R (x))}{\partial s} ((1 - θ) H_{1} (x) + θ H_{2} (x)) d x |}^{2} \\ + 5 {| \int_{n Δ t}^{t} μ (s, R (x)) ((1 - θ) H_{1} (x) + θ H_{2} (x)) d x |}^{2} \\ + 5 {| \int_{n Δ t}^{t} ((1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{2} (x))) d x |}^{2} \\ + 5 {| \int_{n Δ t}^{t} z (\bar{r} (x), H_{1} (x)) d W_{x} |}^{2}, \end{array}$

由Cauchy-Schwarz不等式可得

$5 {| \int_{n Δ t}^{t} \frac{\partial V_{x}}{\partial s} g (s, R (x)) d x |}^{2} \leq 5 {\int_{n Δ t}^{t} | \frac{\partial V_{x}}{\partial s} |}^{2} d x \int_{k Δ t}^{t} {| g (s, R (x)) |}^{2} d x \leq 5 g_{2}^{2} Δ t \int_{n Δ t}^{t} {| \frac{\partial V_{x}}{\partial s} |}^{2} d x$

和

$\begin{array}{l} 5 {| \int_{n Δ t}^{t} \frac{\partial g (s, R (x))}{\partial s} ((1 - θ) H_{1} (x) + θ H_{2} (x)) d x |}^{2} \\ \leq 5 \int_{n Δ t}^{t} {| \frac{\partial g (s, R (x))}{\partial s} |}^{2} d x \int_{n Δ t}^{t} {| (1 - θ) H_{1} (x) + θ H_{2} (x) |}^{2} d x \\ \leq 5 g_{3}^{2} Δ t \int_{n Δ t}^{t} {| (1 - θ) H_{1} (x) + θ H_{2} (x) |}^{2} d x \\ \leq 10 g_{3}^{2} Δ t [\int_{n Δ t}^{t} {| H_{1} (x) |}^{2} d x + \int_{n Δ t}^{t} {| H_{2} (x) |}^{2} d x], \end{array}$

同理

$5 {| \int_{n Δ t}^{t} μ (s, R (x)) ((1 - θ) H_{1} (x) + θ H_{2} (x)) d x |}^{2} \leq 10 α^{2} Δ t [\int_{n Δ t}^{t} {| H_{1} (x) |}^{2} d x + \int_{n Δ t}^{t} {| H_{2} (x) |}^{2} d x]$

和

$5 {| \int_{n Δ t}^{t} (1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{2} (x)) d x |}^{2} \leq 10 Δ t K_{i}^{2} [\int_{n Δ t}^{t} {| H_{1} (x) |}^{2} d x + \int_{n Δ t}^{t} {| H_{2} (x) |}^{2} d x],$

进一步，可得

利用引理1、假设条件(1)~(3)、Doob不等式得

$\begin{array}{l} E [\sup_{0 \leq t \leq T} {| V_{t} - H_{1} (t) |}^{2}] \leq 5 g_{2}^{2} Δ t {\int_{0}^{T} | \frac{\partial V_{x}}{\partial s} |}^{2} d x + 20 g_{3}^{2} Δ t K_{i}^{2} C_{1} + 20 α^{2} Δ t K_{i}^{2} C_{1} \\ + 20 Δ t K_{i}^{2} C_{1} + 5 \max_{n = 1, 2, 3, \dots, N - 1} \int_{n Δ t}^{(n + 1) Δ t} {| z (\bar{r} (x), H_{1} (x)) |}^{2} d s \\ \leq 5 g_{2}^{2} Δ t \int_{0}^{T} {| \frac{\partial V_{x}}{\partial s} |}^{2} d x + 20 g_{3}^{2} Δ t K_{i}^{2} C_{1} \\ + 20 α^{2} Δ t K_{i}^{2} C_{1} + 20 Δ t K_{i}^{2} C_{1} + 5 \max_{i \in s} {K_{i}} C_{1} Δ t, \end{array}$

综上，可得

$E [\sup_{0 \leq t \leq T} {| V_{t} - H_{1} (t) |}^{2}] \leq C_{2} Δ t,$

其中 $C_{2} = 5 g_{2}^{2} {\int_{0}^{T} | \frac{\partial V_{x}}{\partial s} |}^{2} d x + 20 g_{3}^{2} K_{i}^{2} C_{1} + 20 α^{2} K_{i}^{2} C_{1} + 20 K_{i}^{2} C_{1}$ .

同理 $E [\sup_{0 \leq t \leq T} {| V_{t} - H_{2} (x) |}^{2}] \leq C_{3} Δ t$ ，引理2得证。

引理3 假设条件(1)~(3)成立，则存在正常数C₄，使得

$E [\sup_{0 \leq t \leq T} {| V_{t \land δ_{n}} |}^{2}] \leq C_{4},$

其中 $τ_{n} = \inf {t \geq 0; | P_{t} | \geq n}, σ_{n} = \inf {t \geq 0; | V_{t} | \geq n}, δ_{n} = τ_{n} \land σ_{n}$ 。

证明：将Itô引理作用于 ${| V_{t \land δ_{n}} |}^{2}$

$\begin{array}{l} {| V_{t \land δ_{n}} |}^{2} = {| V_{0} |}^{2} + 2 \int_{0}^{t \land δ_{n}} 〈 - \frac{\partial V_{x}}{\partial s} g (s, R (t)), V_{x} 〉 d x \\ + 2 \int_{0}^{t \land δ_{n}} (- \frac{\partial g (s, R (t))}{\partial s} ((1 - θ) H_{1} (x) + θ H_{2} (x)), V_{x}) d x \\ + 2 \int_{0}^{t \land δ_{n}} (- μ (s, R (t)) [(1 - θ) H_{1} (x) + θ H_{2} (x)], V_{x}) d x \\ + 2 \int_{0}^{t \land δ_{n}} ([(1 - θ) f (\bar{r} (x), H_{1} (x)) + θ f (\bar{r} (x), H_{1} (x))], V_{x}) d x \\ + 2 \int_{0}^{t \land δ_{n}} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}) + \int_{0}^{t \land δ_{n}} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x \\ \leq {| V_{0} |}^{2} + 2 \int_{0}^{t \land δ_{n}} 〈 - \frac{\partial V_{x}}{\partial s} g (s, R (t), V_{x}) 〉 d x + 4 \int_{0}^{t \land δ_{n}} (g_{3} + μ_{0}) K_{i} | V_{x} | {‖ V_{x} ‖}_{C} d x \\ + 4 \int_{0}^{t \land δ_{n}} K_{i} | V_{x} | {‖ V_{x} ‖}_{C} d x + \int_{0}^{t \land δ_{n}} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x + 2 \int_{0}^{t \land δ_{n}} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x}), \end{array}$

由引理1可知 $〈 - \frac{\partial V_{x}}{\partial s} g (s, R (t), V_{x}) 〉 \leq \frac{1}{4} g_{1} M^{2} β^{2} {| V_{x} |}^{2}$ ，

$\begin{array}{l} E [\sup_{t \in [0, T]} {| V_{t \land δ_{n}} |}^{2}] \leq E {| V_{0} |}^{2} + \frac{1}{2} g_{1} M^{2} β^{2} E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| V_{x} |}^{2} d x] \\ + 4 (g_{3} + μ_{0} + 1) K_{i} E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| V_{x} |}^{2} d x] \\ + 2 E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} (V_{x}, z (\bar{r} (x), H_{1} (x))) d W_{x}] . \end{array}$

存在一个正常数K₂，由Burkholder-Davis-Gundy不等式可得

$\begin{array}{l} E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} (V_{x}, z (\bar{r} (x), H_{1} (x)) d W_{x})] \\ \leq 3 E [\sup_{t \in [0, T]} | V_{x} | {(\int_{0}^{t \land δ_{n}} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x)}^{\frac{1}{2}}] \\ \leq \frac{1}{4} E [\sup_{t \in [0, T]} {| V_{x} |}^{2}] + K_{2} \int_{0}^{t \land δ_{n}} {‖ z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x \\ \leq \frac{1}{4} E [\sup_{t \in [0, T]} {| V_{x} |}^{2}] + K_{2} K_{i}^{2} \int_{0}^{t \land δ_{n}} E {[\sup_{t \in [0, T]} {‖ V_{x} ‖}_{C}]}^{2} d x \end{array}$

和

$E [\sup_{t \in [0, T]} {| V_{t \land δ n} |}^{2}] \leq 2 E {| V_{0} |}^{2} + (g_{1} M^{2} β^{2} + 8 K_{i} (g_{3} + μ_{0} + 1) + K_{i} + 4 K_{2} K_{i}^{2}) \int_{0}^{t \land δ_{n}} E [\sup_{t \in [0, T]} {| V_{x} |}^{2}] d x .$

综上所述 $E [\sup_{t \in [0, T]} {| V_{t \land δ n} |}^{2}] \leq C_{4}$ ，其中 $C_{4} = 2 E {| V_{0} |}^{2} e^{(g_{1} M^{2} β^{2} + 8 K_{i} (g_{3} + μ_{0} + 1) + K_{i} + 4 K_{2} K_{i}^{2}) T}$ ，引理3得证。

引理4 对任意的 $t \in [0, T]$ ，存在正常数C₅，C₆，使得

$\begin{array}{l} E [\int_{0}^{t \land δ_{n}} {| f (\bar{r} (x), V_{x}) - f (r (x), V_{x}) |}^{2} d x] \leq C_{5} Δ t + ο (Δ t), \\ E [\int_{0}^{t \land δ_{n}} {‖ z (\bar{r} (x), V_{x}) - z (r (x), V_{x}) ‖}^{2} d x] \leq C_{6} Δ t + ο (Δ t) . \end{array}$

证明：参见文献 [17] 中引理7。

引理5 假设条件(1)~(3)成立，存在正常数C₇，使得

$E [\sup_{t \in [0, T]} {| P_{t \land δ n} - V_{t \land δ n} |}^{2}] \leq C_{7} Δ t + ο (Δ t) .$

证明：令 $e_{t \land δ_{n}} = P_{t \land δ n} - V_{t \land δ n}$ ，并对 ${| e_{t \land δ_{n}} |}^{2}$ 应用Itô定理

$\begin{array}{l} {| e_{t \land δ_{n}} |}^{2} = - 2 \int_{0}^{t \land δ_{n}} 〈 g (s, R (x)) \frac{\partial (P_{x} - V_{x})}{\partial s}, P_{x} - V_{x} 〉 d x \\ - 2 \int_{0}^{t \land δ_{n}} [\frac{\partial g (s, R (x))}{\partial s} + μ (s, R (x))] (P_{x} - (1 - θ) H_{1} (x) - θ H_{2} (x), P_{x} - V_{x}) d x \\ + 2 \int_{0}^{t \land δ_{n}} ([(1 - θ) (f (r (x), P_{x}) - f (\bar{r} (x), H_{1} (x))) + θ (f (r (x), P_{x}) - f (\bar{r} (x), H_{2} (x)))], P_{x} - V_{x}) d x \\ + \int_{0}^{t \land δ_{n}} {‖ z (r (x), P_{x}) - z (\bar{r} (x), H_{1} (x)) ‖}_{2}^{2} d x + 2 \int_{0}^{t \land δ_{n}} (z (r (x), P_{x}) - z (\bar{r} (x), H_{1} (x)), P_{x} - V_{x}) d W_{x}, \end{array}$

已知 ${(a + b + c + d + e)}^{2} \leq 5 ({| a |}^{2} + {| b |}^{2} + {| c |}^{2} + {| d |}^{2} + {| e |}^{2})$ ，则

$\begin{matrix} E [\sup_{t \in [0, T]} {| e_{t \land δ_{n}} |}^{2}] \leq 5 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} g (s, R (x)) \frac{\partial (P_{x} - V_{x})}{\partial s} d x |}^{2}] \\ + 5 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} (s, R (x)) ((1 - θ) (P_{x} - H_{1} (x)) + θ (P_{x} - H_{2} (x))) d x |}^{2}] \\ + 5 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} μ (s, R (x)) [(1 - θ) (P_{x} - H_{1} (x)) + θ (P_{x} - H_{2} (x))] d x |}^{2}] \\ + 5 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} (1 - θ) (f (r (x), P_{x}) - f (\bar{r} (x), H_{1} (x))) + θ (f (r (x), P_{x}) - f (\bar{r} (x), H_{2} (x))) d x |}^{2}] \\ + 5 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} z (r (x), P_{x}) - z (\bar{r} (x), H_{1} (x)) d W_{x} |}^{2}], \end{matrix}$

由引理2、Cauchy-Schwarz不等式以及假设条件(1)~(3)得

$\begin{array}{l} E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} \frac{\partial g (s, R (x))}{\partial s} ((1 - θ) (P_{x} - H_{1} (x)) + θ (P_{x} - H_{2} (x))) d x |}^{2}] \\ \leq g_{3}^{2} T {4 E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| (1 - θ) (P_{x} - V_{x}) |}^{2} d x] + 4 E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| (1 - θ) (V_{x} - H_{1} (x)) |}^{2} d x]} \\ + g_{3}^{2} T {4 E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| θ (P_{x} - V_{x}) |}^{2} d x] + 4 E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| θ (V_{x} - H_{2} (x)) |}^{2} d x]} \\ \leq g_{3}^{2} T {8 E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| P_{x} - V_{x} |}^{2} d x] + 4 (C_{2} + C_{3}) Δ t T} \end{array}$

和

$\begin{array}{l} E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} (1 - θ) (f (r (x), P_{x}) - f (\bar{r} (x), H_{1} (x))) + θ (f (r (x), P_{x}) - f (\bar{r} (x), H_{2} (x))) d x |}^{2}] \\ \leq 2 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} f (r (x), P_{x}) - f (\bar{r} (x), V_{x}) + f (\bar{r} (x), V_{x}) - f (\bar{r} (x), H_{1} (x)) d x |}^{2}] \\ + 2 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} f (r (x), P_{x}) - f (\bar{r} (x), V_{x}) + f (\bar{r} (x), V_{x}) - f (\bar{r} (x), H_{2} (x)) d x |}^{2}] \\ \leq 8 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} (f (r (x), P_{x}) - f (\bar{r} (x), V_{x})) d x |}^{2}] + 4 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} f (\bar{r} (x), V_{x}) - f (\bar{r} (x), H_{1} (x)) d x |}^{2}] \\ + 4 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} f (\bar{r} (x), V_{x}) - f (\bar{r} (x), H_{2} (x)) d x |}^{2}] \end{array}$

$\begin{array}{l} \leq 4 \max {K_{i}^{2}} (C_{2} + C_{3}) Δ t T + 16 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} f (r (x), P_{x}) - f (\bar{r} (x), P_{x}) d x |}^{2}] \\ + 16 E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} f (\bar{r} (x), P_{x}) - f (\bar{r} (x), V_{x}) d x] |}^{2}] \\ \leq 16 T [C_{5} Δ t + o (Δ t)] + 16 T \max {K_{i}^{2}} E [\sup_{t \in [0, T]} \int_{0}^{t \land δ_{n}} {| P_{x} - V_{x} |}^{2} d x] + 4 \max {K_{i}^{2}} (C_{2} + C_{3}) Δ t T, \end{array}$

利用Burkholder-Davis-Gundy不等式得

$\begin{array}{l} E [\sup_{t \in [0, T]} {| \int_{0}^{t \land δ_{n}} z (r (x), P_{x}) - z (\bar{r} (x), H_{1} (x)) d W_{x} |}^{2}] \leq 4 E [\int_{0}^{t \land δ_{n}} {| z (r (x), P_{x}) - z (\bar{r} (x), H_{1} (x)) |}^{2} d x] \\ \leq 8 \int_{0}^{t \land δ_{n}} E [{| z (r (x), P_{x}) - z (\bar{r} (x), V_{x}) |}^{2}] d x + 8 \int_{0}^{t \land δ_{n}} E [{| z (\bar{r} (x), V_{x}) - z (\bar{r} (x), H_{1} (x)) |}^{2}] d x \\ \leq 8 \int_{0}^{t \land δ_{n}} E [{| z (r (x), P_{x}) - z (\bar{r} (x), P_{x}) + z (\bar{r} (x), P_{x}) - z (\bar{r} (x), V_{x}) |}^{2}] d x + 8 K_{i}^{2} \int_{0}^{t \land δ_{n}} E {| V_{x} - H_{1} (x) |}^{2} d x \\ \leq 16 \int_{0}^{t \land δ_{n}} E [{| z (r (x), P_{x}) - z (\bar{r} (x), P_{x}) |}^{2}] d x + 16 \int_{0}^{t \land δ_{n}} E [{| z (\bar{r} (x), P_{x}) - z (\bar{r} (x), V_{x}) |}^{2}] d x + 8 K_{i}^{2} C_{5} Δ t \\ \leq 16 (C_{6} Δ t + o (Δ t)) + 16 K_{i}^{2} \int_{0}^{t \land δ_{n}} E [{| P_{x} - V_{x} |}^{2}] d x + 8 K_{i}^{2} C_{5} Δ t, \end{array}$

则

$\begin{array}{l} E [\sup_{t \in [0, T]} {| e_{t \land δ_{n}} |}^{2}] \leq 5 g_{1}^{2} \int_{0}^{t \land δ_{n}} E [{| \frac{\partial (P_{x} - V_{x})}{\partial s} |}^{2} d x + 40 (g_{3}^{2} + α^{2}) T E [\sup \int_{0}^{t \land δ_{n}} {| P_{x} - V_{x} |}^{2} d x] \\ + 20 (g_{3}^{2} + α^{2}) T^{2} Δ t (C_{2} + C_{3}) + 80 T [C_{5} Δ t + o (Δ t)] + 80 T \max {K_{i}^{2}} \\ \cdot E [\sup \int_{0}^{t \land δ_{n}} {| P_{x} - V_{x} |}^{2} d x] + 20 \max {K_{i}^{2}} (C_{2} + C_{3}) Δ t T + 80 (C_{6} Δ t + o (Δ t))] \\ + 80 K_{i}^{2} \int_{0}^{t \land δ_{n}} E [{| P_{x} - V_{x} |}^{2} d x] + 40 K_{i}^{2} C_{5} Δ t, \end{array}$

$\begin{array}{l} \leq 5 g_{1}^{2} \int_{0}^{T} E [{| \frac{\partial (P_{x} - V_{x})}{\partial s} |}^{2}] d x + (40 g_{3}^{2} + 40 α^{2} T + 80 T \max {K_{i}^{2}} + 80 K_{i}^{2}) \\ \cdot \int_{0}^{t \land δ_{n}} E [\sup {| P_{x} - V_{x} |}^{2}] d x + 20 (C_{2} + C_{3}) Δ t T ((g_{3}^{2} + α^{2}) T + \max {K_{i}^{2}}) \\ + 80 T Δ t C_{5} + 80 C_{6} Δ t + ο (Δ t) . \end{array}$

利用Gronwall不等式，有

$E [\sup {| e_{t \land δ_{n}} |}^{2}] \leq C e^{A (t \land δ_{n})} \leq C e^{A T},$

其中

$C = 5 g_{1}^{2} \int_{0}^{T} E [{| \frac{\partial (P_{x} - V_{x})}{\partial s} |}^{2}] d x + 20 (C_{2} + C_{3}) Δ t ((g_{3}^{2} + α^{2}) T^{2} + \max {K_{i}^{2}} T) + 80 T Δ t C_{5} + 80 C_{6} Δ t + o ( Δ t )$

和

$A = 40 g_{3}^{2} + 40 α^{2} T + 80 T \max {K_{i}^{2}} + 80 K_{i}^{2} .$

综上所述， $E [\sup {| e_{t \land δ_{n}} |}^{2}] \leq C e^{A T} + ο (Δ t)$ ，引理5得证。

4. 数值解的收敛性分析

定理1假设条件(1)~(3)成立，则存在正常数C₈，使得

$E [\sup_{0 \leq t \leq T} {| P_{t} - V_{t} |}^{2}] \leq C_{8} Δ t + ο (Δ t) .$

证明：令 $e_{t} = P_{t} - V_{t}$ ，易得

$E [\sup_{0 \leq t \leq T} {| e_{t} |}^{2}] = E [\sup_{0 \leq t \leq T} {| e_{t} |}^{2} I_{[σ_{n} > T and τ_{n} > T]}] + E [\sup_{0 \leq t \leq T} {| e_{t} |}^{2} I_{[σ_{n} < T or τ_{n} > T]}] .$

通过Young不等式，得

$E [\sup_{0 \leq t \leq T} {| e_{t} |}^{2} I_{[σ_{n} < T or τ_{n} > T]}] \leq \frac{Δ t}{2} E [\sup_{0 \leq t \leq T} {| e_{t} |}^{4}] + \frac{1}{2 Δ t} p (σ_{n} < T or τ_{n} > T),$

其中

$E [\sup_{0 \leq t \leq T} {| e_{t} |}^{4}] \leq 8 (E [\sup_{0 \leq t \leq T} {| P_{t} |}^{4}] + E [\sup_{0 \leq t \leq T} {| V_{t} |}^{4}]) \leq 8 (C_{0} + C_{1})$

和

$p (σ_{n} < T) = E [I_{σ_{n} < T} \frac{{| V_{σ_{n}} |}^{4}}{n^{4}}] \leq \frac{1}{n^{4}} E [\sup_{0 \leq t \leq T} {| V_{t} |}^{4}] \leq \frac{C_{0}}{n^{4}}, p (τ_{n} < T) = E [I_{τ_{n} < T} \frac{{| V_{τ_{n}} |}^{4}}{n^{4}}] \leq \frac{C_{1}}{n^{4}} .$

于是，有

$E [\sup_{0 \leq t \leq T} {| e_{t} |}^{2} I_{[σ_{n} < T or τ_{n} > T]}] \leq \frac{Δ t}{2} 8 (C_{0} + C_{1}) + \frac{1}{2 Δ t} \frac{C_{0} + C_{1}}{n^{4}}$

和

$E [\sup_{0 \leq t \leq T} {| e_{t} |}^{2} I_{[σ_{n} > T and τ_{n} > T]}] \leq E [\sup_{0 \leq t \leq T} {| e_{t \land δ_{n}} |}^{2}] .$

由引理5，可得

$E [\sup_{0 \leq t \leq T} {| e_{t \land δ_{n}} |}^{2}] \leq C_{7} Δ t + ο (Δ t),$

若当 $n \geq {(2 Δ t^{2})}^{- \frac{1}{4}}$ ，则有

$E [\sup_{0 \leq t \leq T} {| P_{t} - V_{t} |}^{2}] \leq 4 (C_{0} + C_{1}) Δ t + (C_{0} + C_{1}) Δ t + C_{7} Δ t + ο (Δ t),$

综上，可得

$E [\sup_{0 \leq t \leq T} {| P_{t} - V_{t} |}^{2}] \leq C_{8} Δ t + ο (Δ t),$

其中 $C_{8} = 5 (C_{0} + C_{1}) + C_{7}$ ，定理1得证。

定理2 假设条件(1)~(3)成立，则离散方程(4)的近似解依均方收敛于原方程(1)的解析解

$\lim_{Δ t \to 0} E [\sup_{0 \leq t \leq T} {| P_{t} - V_{t} |}^{2}] = 0.$

证明：由定理1易得。

5. 数值算例

假设 $W (t)$ 是一个标准的Brown运动， $r (t)$ 为右连续的Markov链，状态空间为 $S = {1, 2}$ ，它的生成

元 $Γ = {(γ_{i j})}_{2 \times 2} = (\begin{matrix} - 1 & 1 \\ 2 & - 2 \end{matrix})$ ， $W (t)$ 与 $r (t)$ 相互独立。

本文考虑一个带有Markovian转换的随机尺度结构种群模型的例子：

${\begin{cases} d_{t} P = [- \frac{\partial P (s, t) \frac{1}{s^{2}}}{\partial s} - \frac{1}{{(1 - s)}^{2}} P^{2} (s, t) + f (r (t), P)] d t + z (r (t), P) d W_{t} (s, t) \in Q, \\ P (s, 0) = \exp (- \frac{1}{1 - s}), r (0) = i_{0} = 1 s \in [0, M], \\ P (0, t) = \int_{0}^{T} \frac{1}{{(1 - s)}^{2}} P^{2} (s, t) d s t \in [0, T], \end{cases}$

其中 $Q = [0, T] \times [0, M]$ ，参考 [17] [18] [19] 设置初值。令

$\frac{d R (t)}{d t} = r R (t) (1 - \frac{R (t)}{k}) - (\int_{0}^{M} \frac{r R^{2} (t)}{k M} d s - R (t) \frac{1}{M} \int_{0}^{M} d p (s, t)), R (t) = e^{r + P (s, t)},$

$\begin{array}{l} g (s, R (t)) = \frac{1}{s^{2}}, μ (s, R (t)) = \frac{1}{{(1 - s)}^{2}} (\ln R (t) - r), \\ β (s, R (t)) = \frac{1}{{(1 - s)}^{2}} (\ln R (t) - r), f (1, P) = - P, f (2, P) = \arcsin (P), \\ z (1, P) = \sin (P), z (2, P) = \arctan (P), P_{0} (s) = \exp (- \frac{1}{1 - s}) . \end{array}$

以上初值的设置使随机种群系统满足假设条件(1)~(3)，利用半隐式欧拉数值方法对方程进行离散化处理，通过定理2可知，对任何的 $(s, t) \in [0, M] \times [0, T]$ 都有离散方程的解收敛于原方程的真实解。

令 $Δ t = 0.0008, Δ s = 0.08$ ，在Matlab中输入初始值，得到离散方程关于时间和尺度变化的解。

在利用半隐式欧拉数值方法对模型离散时，当系数 $θ = 1$ 时，即为隐式欧拉方法。可以通过离散方程的解来观察半隐式欧拉方法与隐式欧拉方法的区别。当 $θ = 0 .5$ 时，即为半隐式欧拉数值方法得到的解，见图1。

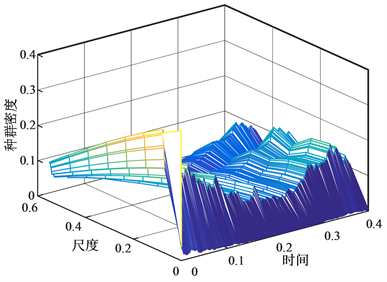
Figure 1. Numerical solution of $θ = 0 .5$ model

图1. 当 $θ = 0 .5$ 时模型的数值解

当 $θ = 1$ 时，即为欧拉数值方法得到的解，见图2。

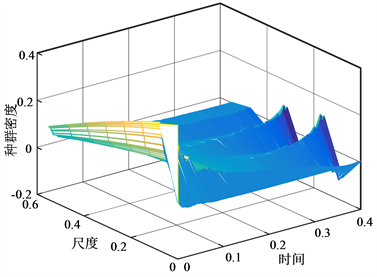
Figure 2. Numerical solution of $θ = 1$ model

图2. 当 $θ = 1$ 时模型的数值解

通过解的图象可以看出当 $t \in [0, 0.1], s \in [0.2, 0.6]$ 时，种群密度的变化最为剧烈，除此之外，种群密度的变化趋于平稳，且隐式欧拉方法和半隐式欧拉方法结果基本趋于一致。

6. 结论

文章主要考虑了带有随机尺度结构种群模型数值解的收敛性问题。由于该模型的精确解很难求得，找出合适的数值方法尤为重要。本文在引入半隐式欧拉数值方法的基础上，利用Itô引理，得到了离散方程的解收敛于原方程的真实解。并提供一个数值例子验证了半隐式欧拉方法的可靠性。

基金项目

国家自然科学基金(11801493)；河北省自然科学基金(A2018203309)。

NOTES

^*通讯作者。

参考文献

[1]	Sauer, T. (2012) Numerical Solution of Stochastic Differential Equations in Finance. Springer, Berlin, 529-550. https://doi.org/10.1007/978-3-642-17254-0_19
[2]	Vlasenko, L.A., Rutkas, A.G. and Chikrii, A.A. (2020) On a Differential Game in a Stochastic System. Proceedings of the Steklov Institute of Mathematics, 309, S185-S198. https://doi.org/10.1134/S0081543820040203
[3]	Cortés, J.-C., Navarro-Quiles, A., Romero, J.-V. and Roselló, M.-D. (2021) Introducing Randomness in the Analysis of Chemical Reactions: An Analysis Based on Random Differen-tial Equations and Probability Density Functions. Compu- tational and Mathematical Methods, 3, 1-10. https://doi.org/10.1002/cmm4.1141
[4]	Zhang, Q.M. and Han, C.Z. (2007) Convergence of Numerical Solutions to Stochastic Age-Structured Population System with Diffusion. Applied Mathematics and Computation, 186, 1234-1242. https://doi.org/10.1016/j.amc.2006.07.156
[5]	Li, R.H., Pang, W.K. and Leung, P.K. (2010) Convergence of Nu-merical Solutions to Stochastic Age-Structured Population Equations with Diffusions and Markovian Switching. Applied Mathematics and Computation, 216, 744-752. https://doi.org/10.1016/j.amc.2010.01.073
[6]	马东娟, 张启敏. 带Poisson跳的随机种群扩散系统半隐式欧拉方法的数值解[J]. 宁夏大学学报(自然科学版), 2010, 31(3): 207-212. https://doi.org/10.3969/j.issn.0253-2328.2010.03.003
[7]	Li, W.R, Ye, M., Zhang, Q.M. and Li, Y. (2020) Nu-merical Approximation of a Stochastic Age-Structured Population Model in a Polluted Environment with Markovian Switching. Numerical Methods for Partial Differential Equations, 36, 1460-1491. https://doi.org/10.1002/num.22488
[8]	Shi, C.M. (2021) The Convergence and Stability of Full Discretization Scheme for Stochastic Age-Structured Population Models. Applied Mathematics and Computation, 396, Article ID: 125867. https://doi.org/10.1016/j.amc.2020.125867
[9]	Itô, K., Kappel, F. and Peichl, G. (1991) A Fully Discre-tized Approximation Scheme for Size-Structured Population Models. Siam Journal on Numerical Analysis, 28, 923-954. https://doi.org/10.1137/0728050
[10]	Ackleh, A.S. and Itô, K. (1997) An Implicit Finite Difference Scheme for the Nonlinear Size-Structured Population Model. Numerical Functional Analysis and Optimization, 18, 865-884. https://doi.org/10.1080/01630569708816798
[11]	Abia, L.M., Angulo, O. and López-Marcos, J.C. (2004) Size-Structured Population Dynamics Models and Their Nume- rical Solutions. Discrete and Continuous Dynamical Systems-Series B, 4, 1203-1222. https://doi.org/10.3934/dcdsb.2004.4.1203
[12]	Angulo, O. and López-Marcos, J.C. (2004) Numerical Integration of Fully Nonlinear Size-Structured Population Models. Applied Numerical Mathematics, 50, 291-327. https://doi.org/10.1016/j.apnum.2004.01.007
[13]	刘炎. 具有Size结构的生物种群动力系统的行为分析和最优控制[D]: [硕士学位论文]. 杭州: 杭州电子科技大学, 2009.
[14]	Liu, Y. and He, Z.-R. (2009) Stability Results for a Size-Structured Population Model with Resources-Dependence and Inflow. Journal of Mathematical Analysis and Ap-plications, 360, 665-675. https://doi.org/10.1016/j.jmaa.2009.07.005
[15]	袁志宏. 一类基于尺度结构种群模型解的适定性[J]. 太原师范学院学报(自然科学版), 2017, 16(4): 1-5.
[16]	刘荣. 几类具有尺度结构的种群模型的最优控制问题[D]: [博士学位论文]. 太原: 山西大学, 2019.
[17]	Li, R.H. and Chang, Z.G. (2007) Convergence of Numerical Solution to Stochastic Delay Differential Equation with Poisson Jump and Markovian Switching. Applied Mathematics and Computation, 184, 451-463. https://doi.org/10.1016/j.amc.2006.06.112
[18]	冯晓龙. 基于MATLAB随机种群模型数值模拟方法的应用研究[J]. 计算机应用与软件, 2014, 31(9): 81-82. https://doi.org/10.3969/j.issn.1000-386x.2014.09.020
[19]	冯晓龙. 具体年龄结构的随机种群模型的研究[D]: [硕士学位论文]. 西安: 西北农林科技大学, 2013: 1-51.

为你推荐

友情链接