1. 引言
本文所考虑的图都是有限、连通、简单无向图。
对于图
,分别用
,
和
表示图
的顶点集,边集和自同构群。设s是一个正整数,称
中
个顶点序列
为一个s-弧,如果
,
,并且对
,有
,
。称
为s-弧传递图,如果
在
的所有s-弧上是传递的。称
为s-传递图,如果
是s-弧传递的,但不是
-弧传递的。
研究群与图里面的对称性,也就是图的自同构群作用在图的顶点集,边集,弧集等上面的传递性,对称图的研究是一个热门的话题,我们研究对称图一般从小度数开始研究。而对于三度图的研究,很多作者都有了一些显著的成果。Chao,Cheng分别在文献 [1] [2] 里完全分类了阶为p和2p的对称图。Conder在文献 [3] 中分类了所有阶小于或等于768个顶点的三度对称图。Tutte在文献 [4] 里给出了三度对称图的点稳定子后,对于三度对称图的分类才得到进一步的研究。Feng在文献 [5] [6] 中分类了8p,10p,8p2,10p2阶的三度对称图。Oh在文献 [7] [8] 里完全分类了14p,16p阶的三度对称图。Cheng在文献 [9] 分类了阶为
的三度对称图。Ling在文献 [10] 中完全分类了四倍的奇无平方整数阶的三度对称图。根据这些研究得到的背景以及结果,可以为我们分类以下的图提供方法。
现在,三度对称图的分类情况已经研究得差不多了,但是40p阶的三度对称图还没有被分类。目前,这篇文章只考虑图自同构群A可解的情况,所以分类不完整,在今后的研究中会继续考虑这个问题,尝试用新的方法来将40p阶的三度对称图完全分类。下面的定理是分类得到的结论。
定理1.1 设
是一个40p阶的三度对称图。令
,F为A的Fitting子群,假设A是可解的,则下列之一成立。
1) F在
上传递,则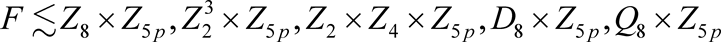 。
。
2) F在
上恰好有两个轨道,F是一个二部图。
3) F在
上至少有三个轨道,
是
的正规覆盖,
是三度的
-弧传递图且
是对称的。
2. 预备知识
在这一节中我们将引用一些基本的结果,方便后面的讨论。设G是有限群,G的所有幂零正规子群的乘积
仍为G的幂零正规子群,叫做G的Fitting子群,下面的引理(参见文献 [11] ,p. 30,推论)。
定理2.1 设
是G的Fitting子群,
不包含
的可解正规子群,若G可解,则
。
对于轨道长公式,有下面的定理,参见文献 [12] 。
定理2.2 设有限群G作用在有限集合
上,
,则
,特别地,轨道
的长是
的因子。
设G是有限群,H是G的子群,
是H在G中的中心化子,
是H在G中的正规。由文( [12] ,第I章,定理5.7)得下面“N/C”定理。
定理2.3 设
,则
同构于
的一个子群。
称Cayley图
是正规的,如果G的右正则表示
是
的正规子群,令:
,令
。设
为
在A中的正规化子,进一步由文献( [13] ,引理2.1)有下面的引理。
引理2.4
。
因此
正规的当且仅当
。
以下引理是关于三度对称图的点稳定子的结构,由( [14] ,命题2~5)确定。
引理2.5 设
是一个连通的五度
-传递图,其中
,
,设
,则下列表述之一成立:
1) 如果
是可解的,则
且
。此外,
见表1。

Table 1. Soluble vertex-stabilizers
表1. 可解的点稳定子
2) 如果
是不可解的,则
且
。此外,
见表2。

Table 2. Insoluble vertex-stabilizers
表2. 非可解的点稳定子
由( [5] ,定理5.1)可以得到8p阶三度对称图的分类。
引理2.6 令p为素数,
是阶为8p的三度对称图,则下列之一成立。
1)
是1-正则的,当
时,
和
。
2)
是2-正则的,当
或7时,
同构于
或Lorimer图。
3)
是3-正则的,当
或5时,
同构于典范双重覆盖图
或
。
对于图
以及点传递子群
,令N是
在
上是不传递的正规子群。用
表示
中的N的轨道的集合,由N诱导的正规商图
定义为顶点集
的图。在商图
中
当且仅当
和
,使得
。文献( [15] ,引理2.5)和( [16] ,定理4.1)为研究三度对称图提供了一种基本的方法。
定理2.7 设
是奇数度的G-弧传递图,令
在
上至少有三个轨道,那么下列的陈述成立。
(i) N是
上的半正则,
,
是
的正规覆盖。
(ii)
,其中
,
。
(iii)
是
-传递的当且仅当
是
-传递。
3. 定理1.1的证明
设
是一个阶为40p的三度对称图,根据引理2.5,
,所以
。接下来,我们考虑A是可解的情况。
证明:设F是A的Fitting子群,根据定理2.1,
,且
,因为
,A没有非平凡的正规s-子群,其中
,p是一个素数,我们有:
。
其中
分别表示A的最大正规2-,5-,p-子群。
对于任意的
,因为A在
上的作用是传递的,
,则
在顶点集
上所有轨道的长都相等。根据定理2.2的轨道公式
,
,再设
在
上有m个轨道,因为
且
时,
,所以
在
上至少有30个轨道。又根据定理2.7(i)可得
在
上是半正则的,此外
,
,
,下面对F进行分情况讨论:
根据
,则8阶群有:循环群
,交换群
,交换群
,非交换群
,非交换群
。
如果F在
上是传递的,当F是交换群时:
,
,
。如果F在
上是传递的,那么
在
是正则的,
是F的Cayley图。设
,其中
,
,因为
,则
是正规Cayley图,根据引理2.4可得
,又因为
是弧传递的,由弧传递的等价条件得知
在
上是传递的,其中1表示
的顶点对应F的单位元,S里的元素都是群F里的元素,对于
,
,使得
,则
,所以S中的元素具有相同的阶,并令其阶为t。当
时,
,有三个单位元,显然是矛盾的,当
时,不能得到矛盾。当F是非交换群时,用所学的知识不能得到矛盾。但是我们有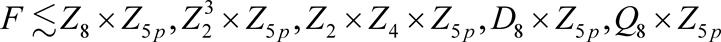 。
。
如果F在
上是至少有三个轨道,则定理2.7(i)表明
是A/F弧传递的,根据假设
时,因为F在
上是半正则的且F为交换群,所以
,又根据引理2.1
,即
。根据定理2.3,
,则
同构于
的一个子群,又因为
,所以
。即
同构于
的一个子群。由于循环群的自同构群是交换群,可得
是交换群,因此A/F是可交换的。由弧传递的等价条件可得对于
,
在它的邻域上传递。因为A/F作用在
上是传递的且是交换群,则A/F是正则的,所以
,出现矛盾。
当F为其它群时,F在
上是至少有三个轨道。在正规块图里面,原图度数与块图的度数相等,则
是
的正规覆盖,
是三度的
-弧传递图。设A存在非平凡的正规子群F且
,设
,
是块图
的两条弧,由块图的定义知道,
。使得
和
是图
的两条弧,于是
,我们有
,
,令
,
,
,
。
,
,
。同理,
,于是
的
对称的。
如果F恰好在
上有两个轨道,根据原图中的轨道个数为块图中的顶点个数,可得块图顶点的个数为2。对于任意的
,设
且
,又设
,
为u在图
中的领域。
,由
得的G-对称性,
,使得
,
,而
,有
,又因为B为块,
,
。从而
,继续这样的推理,
的包含u的连通分支也含于B中。因为
是连通的,只有一条连通分支,且含于B中,
,所以产生矛盾。则B中不含图
的边,这两个轨道就构成了二部图的二部划分,于是
是二部图。
NOTES
*通讯作者。