1. 引言
门式起重机又称龙门吊,是桥式起重机的一种变形,采用门形框架,承载主梁下安装两个支脚,支脚前后各设有滑轮,使其可以在轨道上前后移动,主梁两端具有外伸悬臂梁,外伸悬臂梁可扩大起重机的作业范围 [1] [2] 。本文研究的龙门吊为轨道龙门吊,工作于地铁开挖基坑上方,用于将盾构机排出的土体搬运到基坑外指定位置,在工作过程中需经常依靠轨道变换位置,因此必须保证轨道在龙门吊工作过程中的安全稳定。
贝雷梁起源于英国,由唐纳德·贝雷在1938年第二次世界大战初期设计,后来改进为轻便100型钢桥,经长期使用后发现具有承载力不足、寿命较短等缺点,20世纪90年代英国研制了200型装配式钢桥,我国于20世纪60年代初开始研究装配式钢桥,后来引入英国的贝雷梁装配技术 [3] [4] [5] 。贝雷架是形成的一定单元的桁架,而贝雷梁是由贝雷架组成的桁梁,贝雷梁因其具有结构简单、组合灵活、拼装快、机动性强、可重复利用的特点,被广泛应用于临时架设简易桥梁之中,在国内外军事运输、抢险救灾、工程施工等领域发挥着重要的作用 [6] [7] [8] 。
跨径龙门吊的基础设计要综合考虑龙门吊的结构形式、结构自重、地基承载力、走行形式、架梁设备组装的工作面等要素。采用跨径龙门吊施工时需先用跨径龙门吊架设箱梁作为架桥机、运梁车拼装的工作面,因此在设计跨径龙门吊长度时应保证有足够的长度,以支持运架设备在桥面组拼 [9] [10] [11] 。此外在设计龙门吊基础时要根据龙门吊的结构自重、吊装时最不利荷载受力状况、地基的承载力以及基础的不均匀沉降对跨径龙门吊基础进行综合检算,以确定基础的深度、配筋形式,保证跨径龙门吊的基础有足够的受力特性及较小的不均匀沉降。确保其运营的安全。在基础设计时可根据不同的龙门吊走行形式在基础上设置走行装置预埋件。在跨径龙门吊基础施工时要特别注意地基的实际地质状况与勘测的结果是否相同,若实际地质情况较差,可对基础的结构做相应的调整或对地基进行处理后再进行基础施工 [12] [13] [14] 。
2. 工程概况
本工程为地铁隧道开挖工程,区间全线采用盾构法施工,在车站始发位置开挖基坑,基坑上方悬空假设贝雷梁,贝雷梁上方铺设轨道,用于龙门吊在上方行走搬运盾构施工时管片、渣土、油脂等器材的垂直运输。基坑大小及贝雷梁选取长度如图1所示,根据基坑大小设计贝雷梁长度为14,325 mm,采用层“321”型贝雷桁架拼装。
龙门吊自重160.7 t,最大载重50 t,考虑到龙门吊走时的动荷载,外荷载考虑62.5 t。龙门吊主梁跨度30米,悬臂端单边悬臂,且悬臂有效长度为5米,每侧设计两组轮子,单侧轮距9.4 m,每组共两轮,四根支柱共八个轮,每组轮距0.96 m,轮半径30 cm。贝雷梁初步选择为单排8、10、12片,纵向采用5 m × 3 m (长) × 1.5 m (高) = 15 m,横向宽度约2 m~3 m。
3. 初步计算及材料属性
根据龙门吊的使用工况,将四组轮受力简化为两侧的受力情况,龙门吊起吊时在轨道梁正上方时为最不利荷载,再根据单侧受力将力平均分配到单侧两组(四个)轮子上。
两组轮子最大外力625 KN,共4个轮子,两个轮子为一组,一组外力为312.5 KN。门吊自重1607 KN。一组轮子最大受力
,动载的安全系数取1.4,则一组轮子最大受力1.4 × 714.25 = 1000 KN。
假设每侧每组轮子的压力均匀分配在8、10、12片贝雷梁上。即:
1000 ÷ 8 = 125 KN,则每组轮子向下荷载为125 KN。
1000 ÷ 10 = 100 KN,则每组轮子向下荷载为100 KN。
1000 ÷ 12 = 83.3 KN,则每组轮子向下荷载为83.3 KN。
确定最不利位置为贝雷梁中点位置,简支梁荷载施加简化如图2所示:
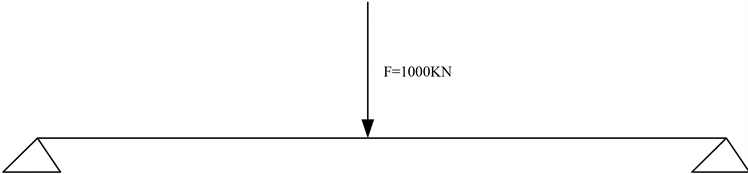
Figure 2. The most unfavorable position of Bailey beam
图2. 贝雷梁最不利位置
贝雷梁基本组成单元是贝雷片。贝雷片由上下弦杆、竖杆及斜杆焊接而成,上下弦杆分别为双][10槽钢,竖杆和斜杆为I8的工字钢,详细参数见表1和表2。

Table 1. Mechanical properties of Bailey beam element bar
表1. 贝雷梁单元杆件力学性能

Table 2. Material, yield strength and allowable stress
表2. 材料、屈服强度及容许应力
4. 数值模拟
4.1. 横向8片贝雷梁稳定性分析
采用Ansys软件进行建模计算,选择beam189作为梁单元进行分析贝雷梁,按照常用贝雷梁参数定义模型参数,即采用Q345钢的物理参数。弹性模量为210 GPa,泊松比为0.3。
横向采用8片贝雷梁计算,单片贝雷梁施加荷载为125 KN,作为简支梁计算。线模型如图3所示,实体模型如图4所示,荷载施加如图5所示。
变形挠度云图如图6所示、轴力云图如图7所示。
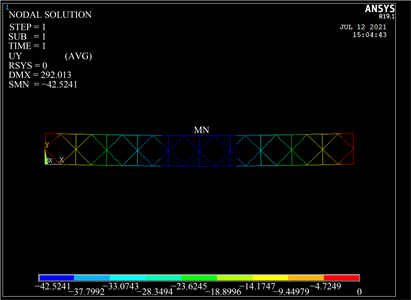
Figure 6. Transverse 8 pieces of Bailey beam deformation deflection cloud diagram
图6. 横向8片贝雷梁变形挠度云图
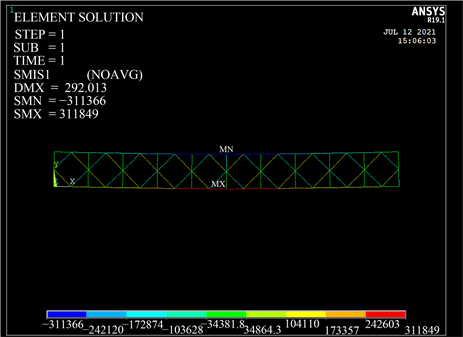
Figure 7. Axial force cloud diagram of 8 transverse Bailey beams
图7. 横向8片贝雷梁轴力云图
根据变形挠度及轴力云图显示,该贝雷梁最大挠度为42.5241 mm,弦杆最大拉应力为311,849 N、最大压应力为311,366 N,竖杆最大轴力为172,894 N,斜杆最大轴力为104,110 N。
强度校核:
弦杆最大轴力值为311,849 N < 560,000 N;竖杆最大轴力为172,894 N < 210,000 N;斜杆最大轴力为104,110 N < 171,500 N;杆件受力满足要求。
通常使用挠跨比校核结构刚度,
;刚度不满足要求。
因此横向采用8片贝雷梁,刚度不符合要求。
4.2. 横向10片贝雷梁稳定性分析
施加荷载为100 KN。梁截面如图8所示。
变形挠度云图如图9所示、轴力云图如图10所示。
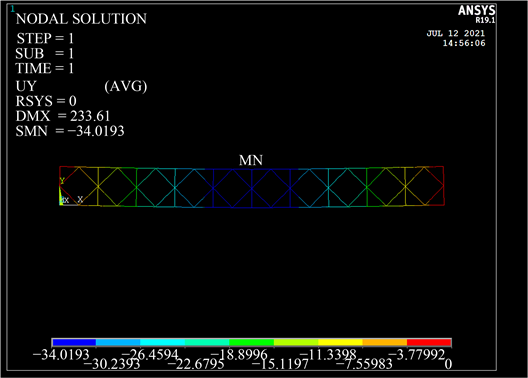
Figure 9. Transverse 10 pieces of Bailey beam deformation deflection cloud diagram
图9. 横向10片贝雷梁变形挠度云图
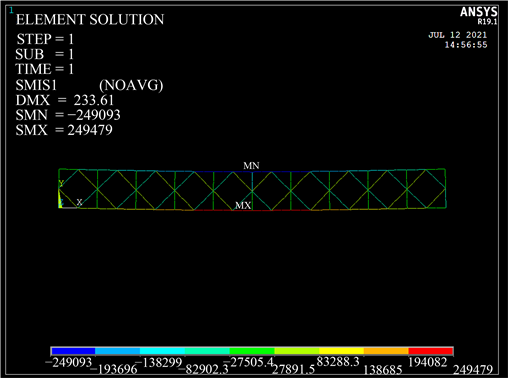
Figure 10. Axial force cloud diagram of 10 transverse Bailey beams
图10. 横向10片贝雷梁轴力云图
根据变形挠度及轴力云图显示,该贝雷梁最大挠度为34.0193 mm,弦杆最大拉应力为249,479 N、最大压应力为249,093 N,竖杆最大轴力为138,299 N,斜杆最大轴力为83,288.3 N。
强度校核:
弦杆最大轴力值为249,479 N < 560,000 N;竖杆最大轴力为138,299 N < 210,000 N;斜杆最大轴力为83,288.3 N < 171,500 N;杆件受力满足要求。
使用挠跨比校核结构刚度,
;刚度满足要求。横向采用10片贝雷梁,杆件受力与结构刚度都满足要求。
4.3. 横向12片贝雷梁稳定性分析
施加荷载为83.3 KN,变形挠度云图如图11所示、轴力云图如图12所示。
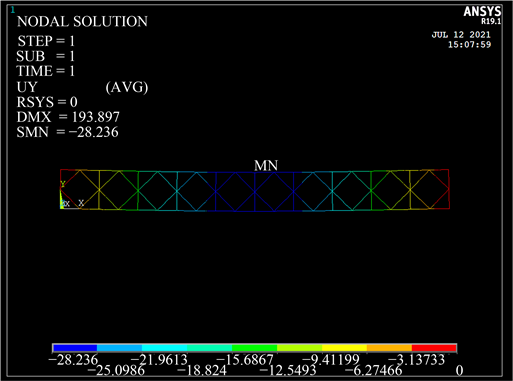
Figure 11. Transverse 12 pieces of Bailey beam deformation deflection cloud diagram
图11. 横向12片贝雷梁变形挠度云图
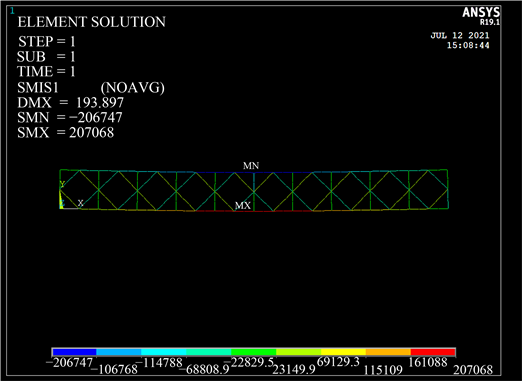
Figure 12. Axial force cloud diagram of 12 transverse Bailey beams
图12. 横向12片贝雷梁轴力云图
根据变形挠度及轴力云图显示,该贝雷梁最大挠度为28.236 mm,弦杆最大拉应力为207,068 N、最大压应力为206,747 N,竖杆最大轴力为114,788 N,斜杆最大轴力为69,129.3 N。
强度校核:
弦杆最大轴力值为207,068 N < 560,000 N;竖杆最大轴力为114,788 N < 210,000 N;斜杆最大轴力为69,129.3 N < 171,500 N;杆件受力满足要求。
挠跨比校核结构刚度,
;刚度满足要求。
5. 总结
本文通过数值模拟的方法,分别分析了横向8片、10片、12片贝雷梁稳定性,结果表明8片贝雷梁的强度满足设计要求,但刚度不满足要求;10片贝雷梁的强度和刚度都满足设计要求;12片贝雷梁的强度和刚度都满足设计要求,但其性能产生了浪费的情况;综合比较,10片贝雷梁更适用于本工程。