1. 引言
随着现代社会经济的发展,我国城市对快捷交通和节能减排、低能耗的要求日益迫切。有轨电车以其经济性、环保性以及美观舒适性等诸多优点在国内被众多城市所认可并运用 [1] 。现代新型有轨电车分为70%低地板和100%低地板技术2种主要车型。随着对人性化设计理念的追求,70%低地板技术正在逐渐被替代,最近几年国内进行研究和建设的有轨电车线路主要以100%低地板车型为主 [2] 。100%低地板有轨电车指的是整个乘客区域内无台阶的低地板有轨电车。其基本特点运行速度较低、使用独立车轮转向架、没有独立的路权。独立车轮转向架是实现低地板车辆的关键。但是独立车轮的轮缘磨耗要比传统刚性轮对大得多,并且容易脱轨。而且由于有轨电车没有独立的路权,导致槽中的污垢积累,更加提升了其脱轨的风险 [3] 。目前,国内外针对列车脱轨后复轨采用较多的救援设备及方法主要分为3类 [4] :① 起重机救援方法为吊复法;② 牵引机车/复轨器拉复法;③ 液压顶复机具顶复法。
对于列车脱轨后复轨所使用的救援设备相关学者进行了研究,主要集中在两个方面:一是针对不同车型的机车及其使用环境的特殊性设计了新的复轨器;二是为验证设计的复轨器的可靠性和安全性,对其强度进行了校核。相关成果如下,沈岳等 [5] 针对目前行业所用的各种矿车轨道复轨器存在的体积和重量过大、不便于携带、不能单人操作等问题,设计了结构简单的可拆分便携式矿车复轨器。张弛等 [6] 研究了对现有的液压起复装置进行了改进,提出通过采用“凹”形导轨式横移梁避免横移小车横向移动滑脱危险,提高了作业效率和安全性。范晓云 [7] 针对100%低地板有轨电车的车底空间狭窄,复轨救援与常规轨道交通车辆有所不同的特点。对列车各种出轨及轮轴卡死工况下的复轨情况进行分析。韩吉元 [8] 建立了某地铁车体的有限元模型,并对枕外复轨位置复轨与牵引梁位置单点复轨两种复轨方法的车体应力分布进行了有限元计算,找出了两种复轨方式车体上应力最大值及其最大值产生的位置。白付维等 [9] 针对高速动车组车辆结构复杂、下部空间狭小的特点及高速铁路线路特征,研制了高速铁路专用单边复轨器以及用于拉复救援中代替机车进行牵引作业的液压牵引机具,包括牵引油缸、卡轨器、有节定位索及超高压液压泵站等部件。通过有限元方法对关键部件进行了强度校核及结构优化,并在救援基地进行了列车复轨试验,取得了良好的试用效果。
100%低地板有轨电车运行速度较低,路况平缓,发生脱轨后脱轨距离不大,所以100%低地板有轨电车的复轨距离需求不大。但是由于其采用埋入式钢轨,车体与大地之间距离较小,且转向架侧边有用于制动的磁轨。这导致复轨器放置的空间有限,并对复轨器的结构设计和强度提出了更高求。本公司针对上述问题参照铁路上常用的人字形复轨器为蓉2号线上运营的100%低地板有轨电车设计了一种有轨电车单边导向复轨装置 [10] 。本文以设计的新型复轨器为研究对象,基于有限元方法,在仿真软件ABAQUS中计算了HT250、40Cr两种材质复轨器的接触应力,并采用现场试验的方式为仿真计算结果的正确性做支撑。
2. 有限元模型建立
2.1. 网格划分
列车复轨过程中,只有一边复轨器的导向筋对列车车轮具有反作用力,这一反作用力即列车的复轨力。为简化模型和计算时间,将车辆的复轨过程转化为车轮和复轨器的接触过程。基于HyperMesh软件分别对复轨器和车轮进行有限元网格划分。首先对复轨器模型进行几何处理去除了对计算影响较小的倒角和不受载荷和约束的半边平板。六面体网格具有计算效率高、收敛性好、离散误差小的特点。所以复轨器的网格划分均采用3D六面体单元,网格划分后复轨器模型包括30,208个单元和37,409个节点如图1所示。
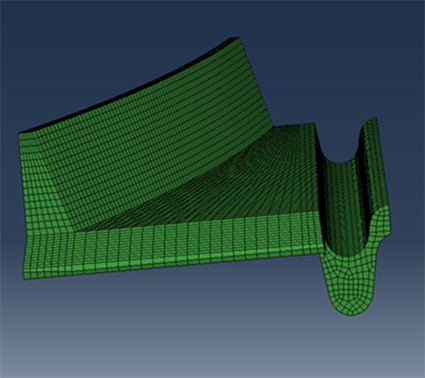
Figure 1. The finite element model of the re-railer
图1. 复轨器有限元模型
为简化车轮模型,只保留车轮与复轨器相接触的下半部分,网格划分也均采用3D六面体单元,车轮模型包括100,608个单元和114,775个节点其模型如图2所示。

Figure 2. The finite element model of the wheel
图2. 车轮有限元模型
2.2. 材料参数
有轨电车车轮的材料为合金钢,其材料参数如表1所示。在复轨器的材料选用上考虑了两种材料分别是HT250和40Cr。HT250复轨器采用铸造工艺加工而成具有质量轻;制造成本低廉;强度、耐磨性、耐热性较好的特点。40Cr复轨器采用数控机床切割而成,质量和制造成本较HT250复轨器高,但强度和硬度更高,HT250和40Cr的材料参数如表1所示。

Table 1. A variety of material parameters
表1. 各种材料参数表
2.3. 接触设置
ABAQUS中提供了单面接触、点面接触和面面接触等多种可供隐式分析使用的接触算法。本模型分析车轮和复轨器的静力学接触,定义复轨器导向筋内侧面为主面,车轮侧轮缘面为从面,法向行为采用硬接触表示接触面之间能够传递压力大小不受限制,切向行为采用罚函数,罚函数法是一种常用的数值方法,它可以模拟两个物体之间的接触力和摩擦力,从而更加准确的预测物体的运动和变形,摩擦系数设为0.25。
2.4. 边界与载荷条件
首先对复轨器进行受力分析:有轨电车受到两个力一个是竖直方向的重力,另一个是水平方向的牵引力,这两个力分别造成了复轨器垂向和横向的载荷。车轮从斜平板上进入复轨器时是复轨器受到垂向载荷的最薄弱的地方,但斜平板在复轨器的结构中只起到导入车轮的作用,因此忽略对该区域的强度分析,只对复轨器平板上的垂向载荷进行分析。为简化计算假设牵引力作用在车轮上,复轨器有轨电车受到的牵引力的方向与轨槽平行,其牵引力分解成两个分量如下图3所示,两个分量中F压会作用在复轨器的导向筋上,使导向筋受到载荷。车轮刚接触到导向筋时其产生的F压的分量最大,导向筋受到的载荷最大,最易发生破坏。所以本次仿真分析选取,车轮刚接触到导向筋时进行接触分析,若本次仿真中复轨器的强度满足其设计要求,则整个复轨过程中复轨器强度也会满足其设计要求。
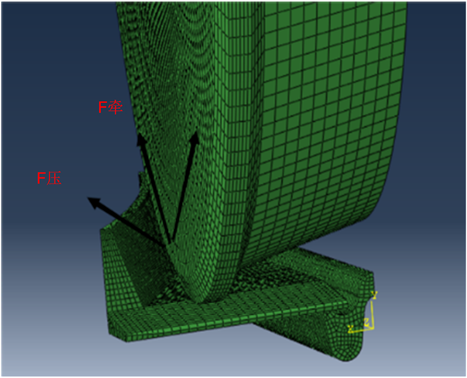
Figure 3. The force analysis diagram of the re-railer
图3. 复轨器受力分析图
复轨器受到的约束为大地和轨槽所提供的摩擦力,复轨过程中复轨器受到大地与轨槽之间的摩擦力静止不动,所以在有限元模型中将复轨器底面设为全约束。查阅有轨电车技术参数其最大轴重为125 kN,则单个车轮受到的重力约为62,500 N。文献 [11] 中经过理论计算得出列车最大启动轮缘牵引力在90.784~100 kN范围内,整列车由五节车箱组成则整车的重力为G = 125 kN*10,摩擦系数取0.25。忽略列车行进过程中的空气阻力,轮缘牵引力减去摩擦力则列车为加速提供的牵引力,经计算其值为68,750 N。车轮受到的载荷前进方向62,500 N,竖直向下方向68,750 N。于是将车轮轴孔面完全固定铰接在轴孔面圆心上,并且在圆心上约束掉除去车轮前进方向和重力方向的4个自由度,在车轮前进方向施加68,750 N的载荷,车轮重力方向施加62,500 N的载荷。
3. 强度分析
3.1. 接触强度计算
利用有限元分析软件ABAQUS分别对有轨电车与HT250复轨器和40Cr复轨器接触过程进行仿真计算。由于车轮与复轨器接触过程中列车是低速匀速行驶,忽略其惯性力,仿真计算使用静力学隐式分析。在仿真计算中HT250复轨器与40Cr复轨器除材料属性不同之外,其它参数设置一致。车轮与HT250复轨器接触点有两个,一个是受重力影响车轮与复轨器平板面上接触,另一个是车轮与导向筋内侧表面。两接触点应力最大值截面云图分别由图4和图5所示。
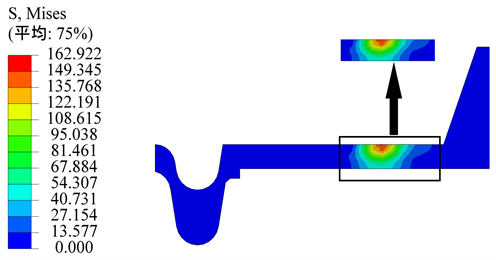
Figure 4. Stress cloud diagram of contact point 1 of HT250 re-railer
图4. HT250复轨器接触点1应力云图
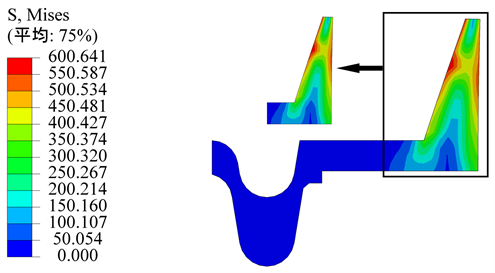
Figure 5. Stress cloud diagram of contact point 2 of HT250 re-railer
图5. HT250复轨器接触点2应力云图
由图可知HT250复轨器最大接触应力发生位置为车轮与导向筋内侧面其最大值为600 MPa,超过了HT250的屈服强度250 MPa,HT250是一种脆性材料最大接触应力超出其强度极限后会发生破损。40Cr复轨器接触点1与接触点2应力最大值截面云图如图6和图7所示。
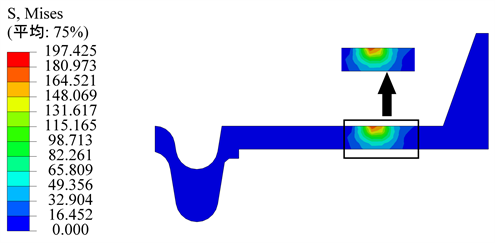
Figure 6. Stress cloud diagram of contact point 1 of 40Cr re-railer
图6. 40Cr复轨器接触点1应力云图
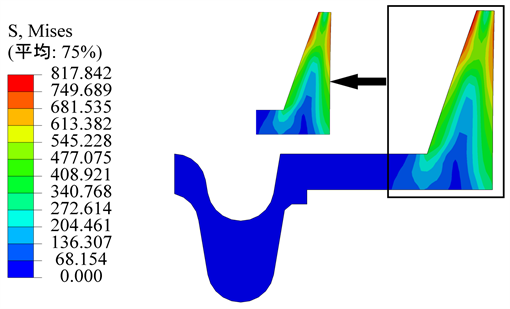
Figure 7. Stress cloud diagram of contact point 2 of 40Cr re-railer
图7. 40Cr复轨器接触点2应力云图
由图可知40Cr复轨器最大接触应力发生位置与HT250复轨器相同其值为818 MPa,超出了40Cr的屈服极限785 MPa。复轨器接触应力的最大值出现在复轨器的导向筋上,有轨电车轮缘内侧与复轨器导向筋内侧面接触类似与车轮与钢轨接触。在铁路上,列车运行一段时间后轮轨接触应力值趋于稳定即处于干磨耗状态,此时轮轨接触最大压应力值会大于钢轨的弹性极限,但此时车轮不发生弹性变形。
弹塑性理论中,对某反复载荷在给定范围内变化时,物体内局部地区发生塑性变形,逐步形成一个残余应力分布,但在有限次作用后,残余应力趋于稳定,而与时间无关,此后残余应力与外载所引起的应力相叠加处处都在弹性范围以内,不再产生新的塑性变形,则这个给定的最大反复载荷就是安定极限载荷,而此状态一般称为安定状态。当载荷超过了安定极限时,塑性变形就将无休止,物体产生塑性流动,最终发生物体累积塑性塌陷。而对于钢轨即为钢轨压馈 [12] 。当载荷小于钢轨的安定极限时车轮不会发生性的塑形变形,参照钢轨的安定极限计算公式(1)得出40Cr的安定极限约为1812 MPa大于40Cr复轨器的最大接触压力818 Mpa,则可以得出40Cr复轨器的强度满足使用要求。
(1)
其中
为安定极限,
为屈服极限。
3.2. 疲劳寿命计算
上节基于静力安定理论对复轨器的强度进行基本分析,本节利用ABAQUS和FE-SAFE联合仿真对40Cr的疲劳寿命进行具体计算。
疲劳问题的分类按照是否超过材料的屈服强度可分为两类:高周疲劳和低周疲劳。高周疲劳当材料没有达到其屈服极限时,疲劳寿命在10万到100万周期之上受到破坏,主要用S-N法。低周疲劳当材料没有达到其屈服极限时,疲劳寿命在几万到几十万周期之下受到破坏,主要用E-N法。由上节计算结果可知:40Cr复轨器的局部区域接触应力最大值超过了其屈服强度所以采用E-N法对复轨器的疲劳寿命进行分析更加合理。当材料发生塑性变形后应变—寿命曲线即E-N曲线更能准确的反应材料的疲劳寿命。在载荷的作用下材料内部组织运动引起循环硬化或软化,应力应变关系与静拉伸的情况下差别较大。Ramberg-Osgood方程是描述材料在其屈服点附近应力与应变关系的方程如式(2)所示。
(2)
其中
为循环强度系数;
为循环应变硬化指数。从文献 [13] 中可知40Cr的循环强度系数为810.5,循环应变硬化指数0.06。将这两个值输入到FE-SAFE中系统可通过Neuber’s rule将为考虑循环硬化的弹性应力应变曲线做适当的转换。将ABAQUS计算所产生的ODB文件导入到FE-SAFE中采用E-N法计算得出40Cr复轨器疲劳寿命最小的区域为上节接触应力超过40Cr屈服极限的区域。最小使用寿命为10^5.521 = 331,895次远大于设计使用寿命不低于10年(每年使用不少于12次)的要求。
4. 试验研究
整车复轨试验在直线线路上进行,新型复轨器采用拉复法进行复轨,有轨电车的超级电容为复轨过程提供牵引力。
有轨电车停在直线线路上,采用液压复轨器将其脱轨,放置好新型复轨器,司机驾驶时切断受电弓使用超级电容供电,从0%,25%,50%,75%,100%依次加至有轨车行驶。有轨电车缓慢经过HT250复轨器。试验发现HT250承受不了有轨电车带来的载荷发生破损如图8所示。证明HT250复轨器的强度不符合复轨要求。

Figure 8. Damage diagram of HT250 re-railer
图8. HT250复轨器破损图
按上述相同步骤对40Cr复轨器进行试验,有轨电车成功复轨并且复轨过程十分平稳未对有轨电车造成损伤。40Cr复轨器复轨后无破损和大变形,仅在导向筋内侧留下一块轻微接触变形区域如图9所示。这是由于导向筋内侧的接触应力超过了40Cr的屈服极限,发生的轻微的塑形变形。基于静力安定定理求出40Cr复轨器的安定极限为1812 MPa大于仿真计算得出的最大接触压力818 Mpa,这表明40Cr复轨器发生塑性变形的区域,会逐渐形成一个残余应力分布,在有限次复轨作用后,残余应力趋于稳定,这片区域将不再产生新的塑性变形,即40Cr复轨器达到安定状态。结合仿真分析和试验验证可以得出40Cr复轨器强度满足车辆复轨的要求。

Figure 9. 40Cr re-railer after re-railing
图9. 复轨后的40Cr复轨器
5. 结论
(1) 在传统人字型复轨器的基础上,基于低地板有轨电车车下结构紧凑等特点,设计出了一种新型的复轨器。在现场复轨试验中,新型复轨器重量较轻单人即可搬运,操作简便,复轨效率高复轨过程仅需30分钟左右,复轨过程平顺且对有轨电车无损伤。相比之前液压复轨器优势明显。
(2) 为所设计的复轨器选取了两种材料,并采用仿真分析和试验验证相结合的方式对两种复轨器的强度进行了校核。仿真分析中HT250复轨器最大接触应力为600 MPa远超出了HT250的屈服极限250 MPa。40Cr复轨器的最大接触应力为818 MPa,基于静力安定理论计算出40Cr复轨器的安定极限为1812 MPa大于仿真计算出的最大接触应力。对40Cr复轨器采用E-N法在FE-SAFE中对其疲劳寿命进行计算的得出结果远大于复轨器的使用要求。
(3) 对设计的两种复轨器进行了现场试验,HT250复轨器在试验中直接破损,40Cr复轨器成功复轨,完成复轨后40Cr复轨器仅在表面留下轻微变形,这与仿真结果相符合,证明设计出的40Cr复轨器在功能和强度上均满足其使用要求。
基金项目
国家自然科学基金青年项目:列车侧向过道岔时轮轨共形接触建模及界面动态力学行为研究(52108418),2021.01-2023.06。
参考文献
NOTES
*第一作者。
#通讯作者。