保积的Lozi映射中与抛物周期点和双曲周期点相关的轨道特征
Orbital Characteristics Related to Parabolic and Hyperbolic Periodic Points in Lozi Area-Preserving Map
DOI: 10.12677/APP.2023.1311048, PDF, HTML, XML, 下载: 145  浏览: 183  科研立项经费支持
作者: 顾恩国, 李 博#：中南民族大学数学与统计学学院，湖北 武汉
关键词: 轨道特征；Lozi保积映射；抛物不动点；双曲不动点；Orbital Characteristics； Lozi Area-Preserving Map； Parabolic Fixed Point； Hyperbolic Fixed Point
摘要: 本文研究了与Lozi保积映射的抛物和双曲周期点相关的轨道特征。证明了其全轨道相对于y=-x都是对称的。首先证明了当a=2时Lozi映射的轨道绕原点旋转，并且指出其轨道可能是发散的，也可能是稳定的周期轨。然后证明了a=-2时Lozi映射的轨道全平面发散，并且发散轨道最终都是属于平行于二四象限的对角平分线的平行直线族。最后证明了当｜a｜＞2时Lozi映射的轨道沿着双曲线在第二或第四象限发散。
Abstract: In this paper, the orbital characteristics associated with a parabolic and hyperbolic periodic point of the Lozi area-preserving map are studied. It is proved that the full trajectory is symmetric about y=-x . We first prove that the trajectory of the Lozi map rotates around the origin, and point out that the trajectory may be divergent or stable periodic when a=2 . Then it is proved that the trajectory of the Lozi map diverges in all planes, and the divergent trajectory eventually belongs to the family of lines parallel to the diagonal bisectors of the two and four quadrants when a=-2 . Finally, it is proved that the trajectory of the Lozi map diverges along the hyperbola in the second or fourth quadrant when ｜a｜＞2 .
文章引用：顾恩国, 李博. 保积的Lozi映射中与抛物周期点和双曲周期点相关的轨道特征[J]. 应用物理, 2023, 13(11): 453-464. https://doi.org/10.12677/APP.2023.1311048

1. 研究背景

为了真正揭示Hénon吸引子的结构，Lozi在1978年提出了一个类似于Hénon映射的简化模型 [1] 。此后，Lozi映射的研究和应用一直没有停止过 [2] - [7] 。Lozi映射在特定参数下存在一个奇异双曲混沌吸引子 [4] [5] 。由Lopesino等人在文 [6] 中证明Lozi映射中存在一个混沌鞍。Cao等人在文 [7] 中提出了Lozi映射参数平面上存在奇异吸引子的开集。但是，当选择特定的参数设置时，Lozi映射就变成了一个特定的二维保持面积映射(后面统一称保积映射)，它可以生成初值相关的无限多个共存不变轨道。DEVANEY等人研究了Lozi映射在 a = 1 时的拓扑共轭模型，并分析了模型的动力学行为 [8] [9] 。最近，LI等人描述了Lozi保积映射中极端依赖初始值的多稳定性 [10] [11] 。

保积映射没有吸引子，但具有丰富而非常复杂的动力学行为，可以提供最简单和最准确的方法来可视化和量化具有两个自由度的保守系统的行为。因此，它们引起了不同领域学者们的关注 [12] - [21] 。SANDER等人开发了一种加权Birkhoff平均方法来识别不依赖于这些对称性的混沌轨道、岛链和旋转不变圆 [17] 。LAGARIAS等人研究了保积同胚的动力学行为 [18] [19] 。GU在文 [20] 中提出了保积映射存在混沌。最近，GU等又研究了与椭圆周期点相关的正则岛链 [21] 。

2. 相关性质和介绍

2.1. 模型介绍

Lozi映射是一种二维分段线性映射，它的数学模型可以写为：

{ x n + 1 = 1 − a | x n | + y n y n + 1 = b x n , (1)

其中，控制参数为两个实常数 a , b ( b ≠ 0 ) ，而(1)式中的Lozi映射的雅可比矩阵可以写成 J = [ − a s i g n ( x ) 1 b 0 ] 。显然，J的行列式是-b，特别是当 b = − 1 ，Lozi映射是一个二维保积映射，可以改写为

T : ( x y ) = { T L ( x , y ) = ( a 1 − 1 0 ) ( x y ) + ( 1 0 ) , x ≤ 0 T R ( x , y ) = ( − a 1 − 1 0 ) ( x y ) + ( 1 0 ) , x > 0 . (2)

为了简单方便，记 A L = ( a 1 − 1 0 ) ， A R = ( − a 1 − 1 0 ) 。 L C − 1 = { ( x , y ) | x = 0 } 被称为基本关键线，即分隔两个映射的定义区域的关键线。 L C = T ( L C − 1 ) = { ( x , y ) | y = 0 } 是(0阶)关键线， L C i = T i ( L C ) 是i阶关键线。为了便于表示，本文将用LC来表示 L C 0 。

2.2. 不动点介绍

系统(2)在两个分区的不动点分别为

L * = ( x L * , y L * ) = ( − 1 a − 2 , 1 a − 2 ) , (3)

R * = ( x R * , y R * ) = ( 1 a + 2 , − 1 a + 2 ) . (4)

如果 L * 和 R * 处于相应的分区，则不动点存在，即“真实”不动点；否则，它们被称为“虚拟”不动点，用 L * ¯ 和 R * ¯ 表示。如果 a = 2 ，那么 L * 是无穷不动点， R * 是真实抛物不动点；如果 a = − 2 ，那么 R * 是无穷不动点， L * ¯ 是虚拟抛物不动点。如果 a > 2 ，那么 L * 和 R * 是真实双曲不动点；如果 a < − 2 ， L * ¯ 和 R * ¯ 是虚拟双曲不动点。

2.3. 性质及其证明

性质1系统(2)的全轨道(包括正向与负向轨)关于 y = − x 都是对称的。

证明Lozi映射T是一个可逆映射，其逆映射是

T − 1 : ( x ′ y ′ ) = { ( 0 − 1 1 − a ) ( x y ) − ( 0 1 ) , y > 0 ( 0 − 1 1 a ) ( x y ) − ( 0 1 ) , y ≤ 0 . (5)

点 A ( x , y ) 相对于线 y = − x 的对称点坐标是 A ′ ( − y , − x ) 。如果 A ( x , y ) 满足(2)式， A ′ ( − y , − x ) 满足(5)式。因此，系统(2)的所有轨道关于 y = − x 都是对称的。证明完毕。

3. 与抛物不动点相关的轨道特征

本节将展示当两个分区的不动点是抛物型时可能的轨道类型，解释为什么发散轨道属于一系列平行直线。

定理1如果 a = 2 ，

1) 存在一个线段 S R : y = x − 1 / 2 , 0 ≤ x ≤ 1 / 2 ，其上任何一点均为二周期环；

2) 全相平面上具有初始条件 ( x 0 , y 0 ) 且不属于直线 S R 的轨道是绕着原点旋转的。

证明令 L = { ( x , y ) | x < 0 , 2 x + y + 1 < 0 } 和 L ¯ = { ( x , y ) | x < 0 , 2 x + y + 1 > 0 } 分别对应图1(a)灰色与天蓝色区域。当 a = 2 ，由系统(2)知

T L : { x ′ = 2 x + y + 1 y ′ = − x ,     T R : { x ′ = − 2 x + y + 1 y ′ = − x . (6)

如果初始点 ( x 0 , y 0 ) ∈ L ， x 1 = 2 x 0 + y 0 + 1 < 0 。因此，在 L 中的轨道保持在左分区。若从 ( x 0 , y 0 ) ∈ L 的轨道上的点 ( x n , y n ) 还在 L 中，则 ( x n y n ) = A L n ( x 0 y 0 ) + ( A L n − 1 + A L n − 2 + ⋯ + A L + I ) ( 1 0 ) , 其中 A L n = ( n + 1 n − n − n + 1 ) .

一个简单的计算表明

x n = x 0 + n ( x 0 + y 0 + n + 1 2 ) , (7)

y n = y 0 − n ( x 0 + y 0 + n − 1 2 ) . (8)

令 R ¯ = { ( x , y ) | x > 0 , − 2 x + y + 1 > 0 } 和 R = { ( x , y ) | x > 0 , − 2 x + y + 1 < 0 } 分别对应于图1(a) 的黄色与绿色区域。从任意 ( x 0 , y 0 ) ∈ R ¯ 出发的轨道通过一次迭代 x 1 = − 2 x 0 + y 0 + 1 > 0 ，因此，在 R ¯ 中的轨道保持在右侧。若从 ( x 0 , y 0 ) ∈ R ¯ 的轨道上的点 ( x n , y n ) 还在 R ¯ 中，则 ( x n y n ) = A R n ( x 0 y 0 ) + ( A R n − 1 + A R n − 2 + ⋯ + A R + I ) ( 1 0 ) , 其中I为单位矩阵， A R n = { ( 2 k + 1 − 2 k 2 k − 2 k + 1 ) , n = 2 k , ( − 2 ( k + 1 ) 2 k + 1 − ( 2 k + 1 ) 2 k ) , n = 2 k + 1.

一个简单的计算表明

{ x 2 n = x 0 + 2 n ( x 0 − y 0 − 1 / 2 ) x 2 n + 1 = − 2 x 0 + y 0 − 2 n ( x 0 − y 0 − 1 / 2 ) + 1 , (9)

{ y 2 n = y 0 + 2 n ( x 0 − y 0 − 1 / 2 ) y 2 n + 1 = − x 0 − 2 n ( x 0 − y 0 − 1 / 2 ) . (10)

1) 当 a = 2 ，系统(2)具有实不动点 R * ( x * , y * ) = ( 1 / 4 , − 1 / 4 ) ，该不动点对应的二重特征值 λ = 1 ，存在唯一过不动点的特征向量 y = x − 1 / 2 ，该特征向量在右分区才真实存在，这导致位于右分区的一个线段 y = x − 1 / 2 ， 0 ≤ x ≤ 1 / 2 ，其上面每一点均是二周期环。

2) 首先证明对于线性系统(2)，从左侧分区出发的轨道最终到达右侧分区。

(7)、(8)式知，对于任意初始条件 ( x 0 , y 0 ) ，有

x n + y n = x 0 + y 0 + n . (11)

方程(11)表明轨道属于直线族 L n : x + y = x 0 + y 0 + n 。

由(9)、(10)式可知，对于任意初始条件 ( x 0 , y 0 ) ，有

{ x 2 n + 1 − y 2 n + 1 = − ( x 0 − y 0 ) + 1 , x 2 n − y 2 n = ( x 0 − y 0 ) . (12)

任取 ( x 0 , y 0 ) ∈ L ，假设从其出发的轨道上的点 ( x n , y n ) 在保持在 L 中，则 x n < 0 并且方程(11)成立，对应充分大的n， 2 x n + y n + 1 = 2 x 0 + y 0 + 1 + n ( x 0 + y 0 + 1 + n + 1 2 ) > 0 恒成立。因此，从 L 区域出发的轨道一定会进入 L ¯ 区域。而在 ( x 0 , y 0 ) ∈ L ¯ 区域的轨道，经过一次迭代 x 1 = 2 x 0 + y 0 + 1 > 0 ， y 1 = − x 0 > 0 就会去往右侧且到达右侧第一象限。然后证明从右侧出发的轨道最终到达左侧分区。

任取 ( x 0 , y 0 ) ∈ R ¯ ，假设从其出发的轨道上的点 ( x n , y n ) 在保持在 R ¯ ，则 x n > 0 并且方程(12)成立，因为 − 2 x 2 n + 1 + y 2 n + 1 + 1 = − x 2 n + 1 + x 0 − y 0 − 1 = 3 x 0 − 2 y 0 − 2 + 2 n ( x 0 − y 0 − 1 / 2 ) ； − 2 x 2 n + y 2 n + 1 = − x 2 n − x 0 + y 0 = − 2 x 0 + y 0 − 2 n ( x 0 − y 0 − 1 / 2 ) 。如果 x 0 − y 0 > 1 / 2 ，n充分大后 − 2 x 2 n + y 2 n + 1 < 0 ；如果 x 0 − y 0 < 1 / 2 ，n充分大后 − 2 x 2 n + 1 + y 2 n + 1 + 1 < 0 。因此，从 R ¯ 区域出发的轨道一定会进入 R 区域。而在 R 区域的轨道，经过一次迭代 x 1 = 2 x n + y n + 1 < 0 ， y 1 = − x n < 0 就会去往左侧且到达左侧第三象限。

(a) a = 2 时轨道不同走向的分区(b) a = − 2 时轨道不同走向的分区

Figure 1. The division of trajectory in different directions in the phase plane at a = ± 2

图1. a = ± 2 时在相平面上轨道不同走向的分区

综上所述， L 区域出发的轨道先去往 L ¯ 区域然后迭代去往右侧分区。它可能直接进入 R 区域然后经过一次迭代返回左侧完成一次循环。也可能进入 R ¯ 区域然后经过若干次迭代在奇数次或偶数次到达 R 区域，最后重新回到 L 区域完成一次循环。所以从相平面任意不属于线段 S R 点出发的轨道绕着原点反复旋转。证明完毕。

由于相平面不属于线段 S R 点出发轨道绕原点不断旋转，如果存在N使得 ( x N , y N ) = ( x 0 , y 0 ) ，则产生一个 N + 1 周期轨道。如果轨道有无限个点并且总体是不断扩张的可能产生一个发散轨道。数值模拟发现在直线族 l n : x + y + n + 1 2 = 0 上的点有可能具有周期性，也有可能发散。取 x 0 = − 1 , y 0 = − 2 , n = 5 有形如 L 6 R L 8 R 这样的周期序列，或者取 x 0 = − 5 , y 0 = 1.5 , n = 6 ，有形如这样 L 9 R L 13 R 的周期点。在射线 y = x − 1 / 2 , x > 1 / 2 上的点有可能具有周期性，也有可能发散。取 x 0 = 3.5 , y 0 = 3 ，有形如 L 13 R 这样的周期序列。

猜想：从直线 x − y − 1 / 2 = 0 与直线族 x + y + n + 1 2 = 0 的交点 P n ( − n 4 , − n + 2 4 ) 出发的轨道必是周期轨。

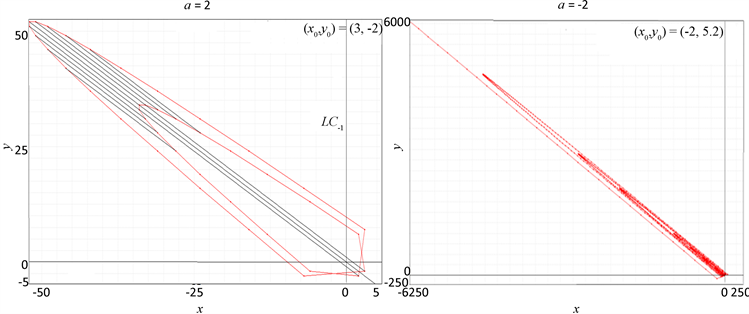
由性质1知，全轨道都是关于 y = − x 对称的。如图2(a)所示，周期轨道关于 y = − x 对称，沿直线族 x + y = x 0 + y 0 + φ 分布。图2(b)显示了初始值为 ( − 2 , 5.2 ) ，迭代次数为1000次的发散轨道，随着迭代次数的增加，发散轨道明显向左侧扩展。

(a) 初始点为 ( 3 , − 2 ) 的周期轨道 (b) 初始点为 ( − 2 , 5.2 ) , n = 1000 的发散轨道

Figure 2. Trajectories characteristics diagram when a = 2

图2. a = 2 时的轨道特征图

定理2如果 a = − 2 ，相平面上任意的初始条件 ( x 0 , y 0 ) 的轨道最终发散并且属于直线族 L n : x + y = x 0 + y 0 + n 。

证明如果 a = − 2 ， T L : { x ′ = − 2 x + y + 1 y ′ = − x ,     T R : { x ′ = 2 x + y + 1 y ′ = − x .

定理2中 T L 和 T R 的作用与定理1中 T R 和 T L 的作用完全相同，但是定理2的映射与定理1的最大不同是没有真实不动点并且无穷不动点位于右侧分区，因此不可能存在二周期线段。下面说明从全平面出发的轨道必然发散。

令 R 1 = { ( x , y ) | x > 0 , x + y + 1 / 2 > 0 } ， R 2 = { ( x , y ) | x > 0 , 2 x + y + 1 > 0 } ， R 3 = { ( x , y ) | x > 0 , x + y + 1 / 2 < 0 , 2 x + y + 1 > 0 } 和 R 1 ¯ = { ( x , y ) | x > 0 , 2 x + y + 1 < 0 } ，其中 R 1 ∪ R 3 = R 2 (对应于图1(b)灰色和白色区域)，在 R 2 中的轨道保持在右侧。首先证明 R 1 (对应于图1(b) 灰色区域)是一个正向不变集，然后证明从 R 1 出发的轨道在第四象限发散并且属于直线族 L n 。

任取 ( x 0 , y 0 ) ∈ R 1 ⊆ R 2 ，假设从其出发的轨道上的点 ( x n , y n ) 保持在 R 2 ，则 x 0 + y 0 + 1 / 2 > 0 ， x n > 0 并且方程(11)成立，所以 2 x n + y n + 1 = x n + x 0 + y 0 + n + 1 = x n + ( x 0 + y 0 + 1 / 2 ) + n + 1 / 2 > 0 恒成立，即 ( x n , y n ) ∈ R 1 。因此， R 1 区域是一个正向不变集。从 ( x 0 , y 0 ) ∈ R 1 出发的轨道一直在右侧的区域 R 1 ，所以式(7)、(8)和(11)对于任意的n成立，又因 x 0 + y 0 + n + 1 2 > x 0 + y 0 + 1 / 2 > 0 ，由(7)和(8)取极限得 lim n → ∞ x n → + ∞ ， lim n → ∞ y n → − ∞ 。因此，轨道在第四象限发散。由(11)式知发散轨道属于平行直线族 L n 。

接着证明 R 3 (对应于图1(b)的白色区域)的轨道一次迭代进入 R 1 。任取 ( x 0 , y 0 ) ∈ R 3 ⊆ R 2 。则 x 1 > 0 。由于 x 1 = 2 x 0 + y 0 + 1 > x 0 + y 0 + 1 / 2 > 0 。即 ( x 1 , y 1 ) ∈ R 1 。最后证明， R 1 ¯ (对应于图1(b)天蓝色区域)的轨道同样进入 R 1 区域。任取 ( x 0 , y 0 ) ∈ R 1 ¯ 经过一次迭代 x 1 = 2 x 0 + y 0 + 1 < 0 ， y 1 = − x 0 < 0 进入左侧第三象限。任取 ( x 0 , y 0 ) ∈ L 1 ¯ = { ( x , y ) | x < 0 , − 2 x + y + 1 < 0 } (对应于图1(b)绿色区域)，类似定理1中关于 R ¯ 区域的方法可以证明从 L 1 ¯ 区域出发的轨道一定会进入 L 1 (对应于图1(b)黄色区域)。从 ( x 0 , y 0 ) ∈ L 1 出发的轨道，经过一次迭代 x 1 = − 2 x 0 + y 0 + 1 > 0 ， y 1 = − x 0 > 0 就会去往右侧且到达右侧第一象限，而第一象限是 R 1 的子集。至此我们证明了左侧出发的轨道必然进入 R 1 ，而 R 1 ¯ 出发的轨道经过一次迭代进入左侧，从而 R 1 ¯ 出发的轨道最终进入 R 1 。因此，相平面上任意点出发的轨道都进入右侧正向不变集 R 1 ，最终在第四象限发散。证明完毕。

4. 与双曲不动点相关的轨道特征

在本节中，将展示当两个分区中的不动点是双曲不动点时可能的轨道类型，解释为什么轨道会沿一系列双曲线发散。

定理4如果 a > 2 ，则从区域 H = { ( x , y ) | x < 0 , λ 1 x + y − λ 1 1 − λ 1 > 0 , a x + y + 1 < 0 } 外出发的轨道沿双曲线不变集 x 2 + a x y + y 2 − x + y + μ = 0 从第二象限发散。

证明首先证明从区域 D = { ( x , y ) | x < 0 , λ 1 x + y − λ 1 1 − λ 1 < 0 } 中出发的轨线必然沿第二象限发散。

由映射(2)定义知，初始条件 ( x 0 , y 0 ) 位于左侧分区的轨道在 T L 作用n次后的点 ( x n , y n ) 为

( x n y n ) = A L n ( x 0 y 0 ) + ( A L n − 1 + A L n − 2 + ⋯ + A L + I ) ( 1 0 ) . (13)

下面计算 A L n ，设 A L n = ( a n b n c n d n ) ，则 A L n = A L A L n − 1 = ( a 1 − 1 0 ) ( a n − 1 b n − 1 c n − 1 d n − 1 ) ，其中：

a n = a ⋅ a n − 1 + c n − 1 ， b n = a ⋅ b n − 1 + d n − 1 ， c n = − a n − 1 和 d n = − b n − 1 。 a n 和 b n 分别是差分方程 a n = a ⋅ a n − 1 − a n − 2 和 b n = a ⋅ b n − 1 − b n − 2 满足于初始条件 a 1 = a , a 2 = a 2 − 1 和 b 1 = 1 , b 2 = − a 的解。这两个差分方程的特征方程为 λ 2 − a λ + 1 = 0 ，则特征值为 λ 1 = a + a 2 − 4 2 ， λ 2 = a − a 2 − 4 2 ，且满足 0 < λ 2 < 1 < λ 1 < a ，因此差分方程的通解为 a n = k 1 λ 1 n + k 2 λ 2 n ； b n = m 1 λ 1 n + m 2 λ 2 n ，由初始条件知 { k 1 λ 1 1 + k 2 λ 2 1 = a k 1 λ 1 2 + k 2 λ 2 2 = a 2 − 1 ,     { m 1 λ 1 1 + m 2 λ 2 1 = 1 m 1 λ 1 2 + m 2 λ 2 2 = a ,

解得 k 1 = λ 1 a 2 − 4 , k 2 = − λ 2 a 2 − 4 , m 1 = 1 a 2 − 4 , m 2 = − 1 a 2 − 4 ,

一个简单的计算表明 A L n = 1 a 2 − 4 ( λ 1 n + 1 − λ 2 n + 1 λ 1 n − λ 2 n λ 2 n − λ 1 n λ 2 n − 1 − λ 1 n − 1 ) ,

将 A L n 带入(13)式中计算得

x n = 1 a 2 − 4 λ 1 n ( λ 1 x 0 + y 0 − λ 1 1 − λ 1 ) + α n , (14)

y n = − 1 a 2 − 4 λ 1 n − 1 ( λ 1 x 0 + y 0 − λ 1 1 − λ 1 ) + β n , (15)

其中 α n = − 1 a 2 − 4 λ 2 n ( λ 2 x 0 + y 0 − λ 2 1 − λ 2 ) + 1 2 − a , β n = 1 a 2 − 4 λ 2 n − 1 ( λ 2 x 0 + y 0 − λ 2 1 − λ 2 ) − 1 2 − a .

注：可知随着n的不断增大，因为 0 < λ 2 < 1 ，故 α n , β n 是无限趋近于 ± 1 a − 2 的数，最终不影响 x n 与 y n 的符号。

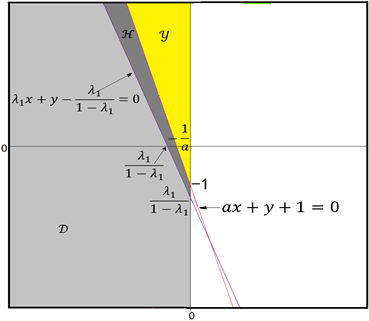
在证明区域D是沿着第二象限发散之前，首先说明直线 l 1 : λ 1 x + y − λ 1 1 − λ 1 = 0 位于直线 l 2 : a x + y + 1 = 0 的左下方。因为 1 1 − λ 1 + 1 a = λ 2 + 1 a ( 1 − λ 1 ) < 0 ，即 1 1 − λ 1 < − 1 a ，所以直线 l 1 在x轴的截距 1 1 − λ 1 小于直线 l 2 在x轴的截距 − 1 a 。而 λ 1 1 − λ 1 + 1 < 0 ，即 λ 1 1 − λ 1 < − 1 ，所以直线 l 1 在y轴的截距 λ 1 1 − λ 1 小于直线 l 2 在y轴的截距−1。因此，直线 l 1 在左侧分区位于直线 l 2 的左下方(如图3(a)所示)。可知当满足 a x 0 + y 0 + 1 > 0 时， λ 1 x 0 + y 0 − λ 1 1 − λ 1 > 0 恒成立；满足 λ 1 x 0 + y 0 − λ 1 1 − λ 1 < 0 时， a x 0 + y 0 + 1 < 0 恒成立。由映射(2)知， ∀ ( x 0 , y 0 ) ∈ D ， x 1 = a x 0 + y 0 + 1 < 0 ，因此， ∀ ( x 0 , y 0 ) ∈ D ，恒有 x n < 0 成立，即轨道一直会在左侧分区运动。

由(14)、(15)式可知， x n 和 y n 的正负最终由 λ 1 x 0 + y 0 − λ 1 1 − λ 1 的正负决定。当 λ 1 x 0 + y 0 − λ 1 1 − λ 1 > 0 时， lim n → ∞ x n = + ∞ ， lim n → ∞ y n = − ∞ ；同理当 λ 1 x 0 + y 0 − λ 1 1 − λ 1 < 0 时， lim n → ∞ x n = − ∞ ， lim n → ∞ y n = + ∞ 。由

上面的证明可知，从左侧分区并且在区域D的点(图3(a)中浅灰色区域)出发的轨道仍然在左侧分区，并且轨道最终沿着第二象限发散。

下面证明从右侧分区出发的轨道必然进入区域D然后沿第二象限发散。由映射(2)定义知，初始条件 ( x 0 , y 0 ) 位于右侧分区的轨道在 T R 作用n次后的点 ( x n , y n ) 为

( x n y n ) = A R n ( x 0 y 0 ) + ( A R n − 1 + A R n − 2 + ⋯ + A R + I ) ( 1 0 ) . (16)

下面计算 A R n ，这里设 A R n = ( a ′ n b ′ n c ′ n d ′ n ) ，可以令 A R n = A R A R n − 1 = ( − a 1 − 1 0 ) ( a ′ n − 1 b ′ n − 1 c ′ n − 1 d ′ n − 1 ) ，其中 a ′ n = − a ⋅ a ′ n − 1 + a ′ n − 1 ， b ′ n = − a ⋅ b ′ n − 1 + d ′ n − 1 ， c ′ n = − a ′ n − 1 和 d ′ n = − c ′ n − 1 。 a ′ n 和 b ′ n 分别是差分方程 a ′ n = a ⋅ a ′ n − 1 − a ′ n − 2 和 b ′ n = a ⋅ b ′ n − 1 − b ′ n − 2 满足于初始条件 a ′ 1 = − a , a ′ 2 = a 2 − 1 和 b ′ 1 = 1 , b ′ 2 = − a 的解。这两个差分方程的特征方程为 λ 2 + a λ + 1 = 0 ，则特征值为 λ 1 = − a − a 2 − 4 2 ， λ 2 = − a + a 2 − 4 2 ，且满足 − a < λ 1 < − 1 < λ 2 < 0 ，由此差分方程的通解为 a ′ n = k ′ 1 λ 1 n + k ′ 2 λ 2 n ； b ′ n = m ′ 1 λ 1 n + m ′ 2 λ 2 n ，由初始条件知 { k ′ 1 λ 1 1 + k ′ 2 λ 2 1 = − a k ′ 1 λ 1 2 + k ′ 2 λ 2 2 = a 2 − 1 ,     { m ′ 1 λ 1 1 + m ′ 2 λ 2 1 = 1 m ′ 1 λ 1 2 + m ′ 2 λ 2 2 = − a ,

解得 k ′ 1 = − λ 1 a 2 − 4 , k ′ 2 = λ 2 a 2 − 4 , m ′ 1 = − 1 a 2 − 4 , m ′ 2 = 1 a 2 − 4 .

一个简单的计算表明 A R n = 1 a 2 − 4 ( λ 2 n + 1 − λ 1 n + 1 λ 2 n − λ 1 n λ 1 n − λ 2 n λ 1 n − 1 − λ 2 n − 1 ) .

将 A R n 带入(16)式中计算得

x n = − 1 a 2 − 4 λ 1 n ( λ 1 x 0 + y 0 − λ 1 1 − λ 1 ) + α ′ n , (17)

y n = 1 a 2 − 4 λ 1 n − 1 ( λ 1 x 0 + y 0 − λ 1 1 − λ 1 ) + β ′ n , (18)

其中 α ′ n = 1 a 2 − 4 λ 2 n ( λ 2 x 0 + y 0 − λ 2 1 − λ 2 ) + 1 2 + a , β ′ n = − 1 a 2 − 4 λ 2 n − 1 ( λ 2 x 0 + y 0 − λ 2 1 − λ 2 ) − 1 2 + a .

注：同理，因为 − 1 < λ 2 < 0 ，可知随着n的不断增大， α ′ n , β ′ n 是无限趋近于 ± 1 2 + a 的数，最终不影响 x n 与 y n 的符号。

由(17)、(18)式知， x n 和 y n 的正负最终由 λ 1 x 0 + y 0 − λ 1 1 − λ 1 的正负决定。随着n不断增加可以知道，当 λ 1 x 0 + y 0 − λ 1 1 − λ 1 > 0 ，n为偶数时， lim n → ∞ x n = − ∞ ， lim n → ∞ y n = − ∞ ；n为奇数时， lim n → ∞ x n = + ∞ ， lim n → ∞ y n = + ∞ 。当 λ 1 x 0 + y 0 − λ 1 1 − λ 1 < 0 ，n为偶数时， lim n → ∞ x n = + ∞ ， lim n → ∞ y n = + ∞ ；n为奇数时， lim n → ∞ x n = − ∞ ， lim n → ∞ y n = − ∞ 。因此，从右侧分区出发、具有初始条件 ( x 0 , y 0 ) 的轨道最终在奇数点或偶数点到达第三象限并且远离原点。因此，最终进入区域D然后从第二象限发散。

然后证明初始点从图3(a)中黄色区域 Y = { ( x , y ) | x < 0 , a x + y + 1 > 0 } 出发的轨道最终进入区域D然后沿第二象限发散。因为若 ( x 0 , y 0 ) ∈ Y ，则 x 1 = a x 0 + y 0 + 1 > 0 。从区域 Y 中点出发的轨线一次迭代就进入右侧分区，由上面分析知最终必然进入区域D然后从第二象限发散。

最后证明轨道沿双曲线不变集发散。由文 [21] 中引理知，如果 | T r ( M ) | > 2 ，那么水平不变集除了在 μ = 0 是过圆锥曲线中心 C 0 ( 4 e s + 2 ( g − d ) t 4 − T r ( M ) 2 , 2 ( g − d ) s − 4 f t 4 − T r ( M ) 2 ) 的渐近线外，其他均是充满全部相平面的双曲线。已经证明当 a > 2 时，从 H 外出发的轨道均发散，所以只能沿着双曲线不变集 x 2 + a x y + y 2 − x + y + μ = 0 发散。证明完毕。

事实上，由上述证明过程可以看出，当 a > 2 时，除非图3(a)深灰色区域 H 为正向不变集，否则从 H 点出发的轨线可能进入区域D也可能经过有限次迭代到达右侧分区，它们最终也在第二象限发散。所以几乎全平面点的轨道最终在第二象限发散。

定理5如果 a < − 2 ，则从区域 H ¯ = { ( x , y ) | x > 0 , λ ′ 1 x + y − λ ′ 1 1 − λ ′ 1 < 0 , − a x + y + 1 > 0 } 外出发的轨道沿双曲线不变集 x 2 − a x y + y 2 − x − a + 2 a − 2 y + μ = 0 从第四象限发散。

证明因为如果 a < − 2 ，则 − a > 2 。由映射(2)知，定理5中 T R 的作用与定理4中 T L 的作用完全相同。由 A R = ( − a 1 − 1 0 ) 的特征方程 λ 2 + a λ + 1 = 0 知 0 < λ ′ 2 < 1 < λ ′ 1 < − a ， a = − λ ′ 1 − 1 λ ′ 1 < − λ ′ 1 ，所以直线 l ′ 2 : − a x + y + 1 = 0 的斜率a小于直线 l ′ 1 : λ ′ 1 x + y − λ ′ 1 1 − λ ′ 1 = 0 的斜率 − λ ′ 1 。而 λ ′ 1 1 − λ ′ 1 + 1 < 0 ，说明直线 l ′ 2 在y轴的截距点 ( 0 , − 1 ) 位于 l ′ 1 在y轴的截距点 ( 0 , λ ′ 1 1 − λ ′ 1 ) 的上方。因此，直线 l ′ 2 在右侧分区与直线 l ′ 1 左相交(如图3(b))。则可以类似证明存在区域 D ¯ = { ( x , y ) | x > 0 , λ ′ 1 x + y − λ ′ 1 1 − λ ′ 1 > 0 , − a x + y + 1 > 0 } (如图3(b)浅灰色区域所示)，使得进入区域 D ¯ 的轨道最终沿着第四象限发散。因此，可以类似证明定理5从区域 H ¯ 外出发的轨道沿双曲线不变集 x 2 − a x y + y 2 − x − a + 2 a − 2 y + μ = 0 在第四象限发散。

(a) a > 2时，轨道初始点取值区域 (b) a < -2时，轨道初始点取值区域

Figure 3. The value region of the initial point where the trajectory diverges along the second and fourth quadrants

图3. 轨道沿着第二、四象限发散的初始点的取值区域

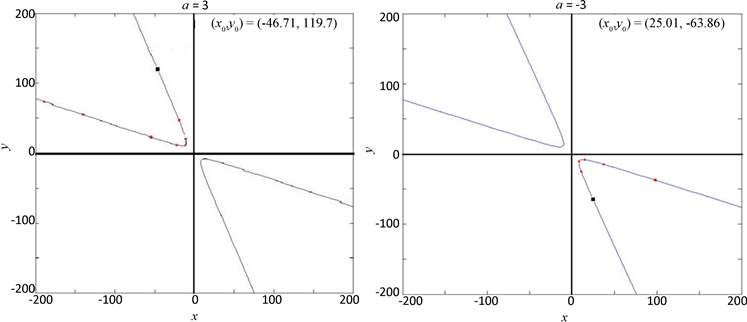
图4显示了当 | a | = 3 时的轨道特征图。图4(a)由 a = 3 和初始值 ( − 46.71 , 119.7 ) 迭代1200次得到，轨道最终在第二象限沿着双曲线 x 2 + 3 x y + y 2 − x + y + 100 = 0 的左分支发散到无穷远。图4(b)由 a = − 3 和初始值为 ( 25.01 , − 63.86 ) 迭代1200次得到，轨道最终在第四象限沿着双曲线 x 2 − 3 x y + y 2 − x − 0.2 y + 100 = 0 的右分支向无穷远发散。

5. 总结

本文发现保积Lozi映射有非常复杂的轨道，它不仅取决于系统的参数，还取决于初始值和迭代次数。证明了保积Lozi映射的所有轨道关于直线 y = − x 是对称的。当两侧不动点为抛物不动点时，当 a = 2 在线段

(a) a = 3 时，过初始点为 ( − 46.71 , 119.7 ) 的 (b) a = − 3 时，过初始点为 ( 25.01 , − 63.86 ) 的双曲线 x 2 + 3 x y + y 2 − x + y + 100 = 0 的轨道 双曲线 x 2 + 3 x y + y 2 − x − 0.2 y + 100 = 0 的轨道

Figure 4. Trajectories characteristics diagram when | a | > 2

图4. | a | > 2 时的轨道特征图

S R 上任取一点存在一个稳定二周期轨道，而取点不在线段 S R 上轨道绕着原点旋转；当 a = − 2 时，从相平面上任意点出发的轨道均为发散轨道，并且系统发散轨道都属于直线族 x + y = x 0 + y 0 + n 。当两侧不动点为双曲不动点时，运用差分方程的计算方法来描述双曲不动点的轨道特征，发现几乎从全相平面上任意一点出发

的轨道最终都沿着双曲线不变集 x 2 + a x y + y 2 − x + y + μ = 0 或者 x 2 − a x y + y 2 − x − a + 2 a − 2 y + μ = 0 发散。

基金项目

中南民族大学研究生学术创新基金资助项目(3212023sycxjj005)。

参考文献

[1] Lozi, R. (1978) Un Attracteur étrange (?) du type attracteur de Hénon. Journal de Physique Colloque, 39, 5-9.
https://doi.org/10.1051/jphyscol:1978505
[2] Misiurewicz, M. and Štimac, S. (2016) Symbolic Dynamics for Lozi Maps. Nonlinearity, 29, 3031-3046.
https://doi.org/10.1088/0951-7715/29/10/3031
[3] Gupta, C., Holland, M. and Nicol, M. (2011) Extreme Value Theory for Sinai Dispersing Billiards, Lozi Maps and Lorenz Like Maps. Ergodic Theory and Dynamical Systems, 31, 1363-1390.
https://doi.org/10.1017/S014338571000057X
[4] Botella-Soler, V., Castelojm, J.M., Oteo, J.A., et al. (2011) Bifurcations in the Lozi Map. Journal of Physics A: Mathematical and Theoretical, 44, Article ID: 305101.
https://doi.org/10.1088/1751-8113/44/30/305101
[5] Rybalova, E., Semenova, N., Strelkovag, G., et al. (2017) Transition from Complete Synchronization to Spatio-Temporal Chaos in Coupled Chaotic Systems with Nonhyperbolic and Hyperbolic Attractors. European Physical Journal Special Topics, 226, 1857-1866.
https://doi.org/10.1140/epjst/e2017-70023-1
[6] Lopesino, C., Balibrea-Iniesta, F., Wiggins, S., et al. (2015) The Chaotic Saddle in the Lozi Map, Autonomous and Nonautonomous Versions. International Journal of Bifur-cation & Chaos, 25, Article ID: 1550184.
https://doi.org/10.1142/S0218127415501849
[7] Cao, Y. and Liu, Z. (1998) Strange Attractors in the Ori-entation-Preserving Lozi Map. Chaos Solitons and Fractals, 9, 1857-1864.
https://doi.org/10.1016/S0960-0779(97)00180-X
[8] Devaney, R.L. (1984) A Piecewise Linear Model for the Zones of Instability of an Area-Preserving Map. Physica D: Nonlinear Phenomena, 10, 387-393.
https://doi.org/10.1016/0167-2789(84)90187-8
[9] Aharonov, D., Devaney, R.L., Elias, U. (1997) The Dy-namics of a Piecewise Linear Map and Its Smooth Approximation. International Journal of Bifurcation and Chaos, 7, 351-372.
https://doi.org/10.1142/S0218127497000236
[10] Li, H., Li, K., Chen, M., et al. (2020) Coexisting Infinite Orbits in an Area-Preserving Lozi Map. Entropy, 22, Article 1119.
https://doi.org/10.3390/e22101119
[11] Li H, Bao H, Zhu L, et al. (2020) Extreme Multistability in Simple Area-Preserving Map. IEEE Access, 8, 175972-175980.
https://doi.org/10.1109/ACCESS.2020.3026676
[12] Rybalova, E. and Strelkova, G. (2022) Response of Sol-itary States to Noise-Modulated Parameters in Nonlocally Coupled Networks of Lozi Maps. Chaos, 32, Article ID: 021101.
https://doi.org/10.1063/5.0082431
[13] Zheng, W.M. and Liu, J. (1994) Symbolic Analysis of At-tractor Geometry for the Lozi Map. Physical Review E, 50, 3241-3244.
https://doi.org/10.1103/PhysRevE.50.3241
[14] Duarte, P. (1994) Plenty of Elliptic Islands for the Standard Family of Area Preserving Maps. Annales De Linstitut Henri Poincare, 11, 359-409.
https://doi.org/10.1016/s0294-1449(16)30180-9
[15] Reichl, L.E. (1992) The Transition to Cha-os/Conservative Classical Systems and Quantum Manifestations. Springer-Verlag, New York.
[16] Rybalova, E.V., Strelkovag, I. and Anishchenko, V.S. (2020) Impact of Sparse Inter-Layer Coupling on the Dynamics of a Heter-ogeneous Multilayer Network of Chaotic Maps. Chaos, Solitons & Fractals, 142, Article ID: 110477.
https://doi.org/10.1016/j.chaos.2020.110477
[17] Sander, E. and Meissj, D. (2020) Birkhoff Averages and Rotational Invariant Circles for Area-Preserving Maps. Physica D: Nonlinear Phenomena, 411, Article ID: 132569.
https://doi.org/10.1016/j.physd.2020.132569
[18] Lagarias, J.C. and Rains, E. (2005) Dynamics of a Family of Piecewise-Linear Area-Preserving Plane Maps I, Rational Rotation Numbers. Journal of Difference Equations and Applications, 11, 1089-1108.
https://doi.org/10.1080/10236190500273069
[19] Lagarias, J.C. and Rains, E. (2005) Dynamics of a Family of Piecewise-Linear Area-Preserving Plane Maps II, Invariant Circles. Journal of Difference Equations and Applications, 11, 1137-1163.
https://doi.org/10.1080/10236190500273127
[20] Gu, E.G. (2018) On the Existence of Chaos in a Discon-tinuous Area-Preserving Map Arising in Financial Markets. International Journal of Bifurcation and Chaos, 28, Article ID: 1850177.
https://doi.org/10.1142/S0218127418501778
[21] Gu, E.G., He, Z.H., Ni, J., et al. (2023) Invariant Regions in Piecewise Linear Area-Preserving Map. Chaos Soliton and Fractals, 169, Article ID: 113308.
https://doi.org/10.1016/j.chaos.2023.113308

为你推荐