1. 引言
2009年,文献 [1] 中证明了
-John域上作用于微分形式复合算子
的Poincaré-型嵌入不等式
(1)
其中
为同仑算子T与投影算子H的复合算子,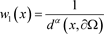 ,
,常数
满足
,微分形式u满足非齐次A-调和方程
。
,
,常数
满足
,微分形式u满足非齐次A-调和方程
。
2014年,文献 [2] 给出了复合算子
的如下Poincaré-型不等式
(2)
其中
为Hardy-Littlewood极大算子、P为potential算子,
为
上的一有界凸区域。
2020年,文献 [3] 给出了如下作用于Dirac-调和方程
的光滑微分形式的迭代算子
的局部
-权
-积分不等式。
(3)
这里D是Dirac算子,
,
,
,
,
。
显然,上述结果均是用微分形式的
-范数去估计算子的
-范数,如式(2)以微分形式的加权
-范数
去估计Potential算子P加权
-范数
,若
,则Potential算子P的
-范数
就无法用式(2)中的微分形式的
-范数
来估计了,此时就需要讨论Potential算子
是否具有比微分形式更高阶的范数。称算子范数高于微分形式范数的研究为算子的高阶范数研究。由于复合算子的范数估计远比单算子的范数估计复杂,故本文选择复合算子
的高阶可积性作为研究内容,分别在
与
条件下证明了复合算子
的局部高阶可积性。
2. 记号及预备知识
微分形式是
上可微函数的推广,称函数
为微分0-形式,称
是微分l-形式,其中有序l-丛
,
,
,关于的微分形式的相关结果可参见文献 [4] - [10] 。记
(
)是n维欧氏空间,
是
上有界子集,其勒贝格测度记为
。设B与
是
中具有相同球心的球体,其直径满足
。记d为外微分算子,
表示由全体微分l-形式所成的l-维向量空间。设
是一微分l-形式,定义作用于
上的Hodge星算子
为
其中
,
,
。利用外微分算子d和Hodge星算子
定义Hodge上的微分算子
,
。如在
中,取微分形式
则
且
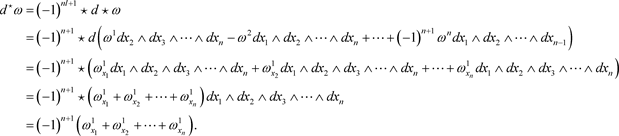
称下列非线性偏微分方程
(4)
为齐次A-调和方程,其中算子
对几乎所有的
,
,满足
上述
为一常数且
是与方程(4)有关的确定指数。定义同仑算子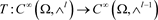 为
为
其中
,
满足
,线性算子
满足
记G为定义在
上的Green算子,且满足Poisson方程
,其中H为调和投影算子。更多关于A-调和方程、同仑算子与Green算子的介绍及相关成果可参见文献 [11] 。
在本文相关结论的证明将应用到下述引理。
引理1 [12] 设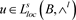 是球体B上的一微分形式,
,
,则
是球体B上的一微分形式,
,
,则
(5)
(6)
引理2 [13] 设u是
上一光滑微分形式,
,则对
上任一球体B,存在一不依赖于u的常数C,使得
引理3 [12] 设
,
,则
,且
其中Q为
上一球体,
,
。
引理4 [14] 设u是
上满足A-调和方程(4)的一微分形式,则对所有满足
的球体B,存在一不依赖于u的常数C,使得
其中
,
。
引理5 [15] 设
为
上的一有界域,
是定义在
上的单调递增凸函数且满足
。若微分形式
,
,则
,且对任一实数
有
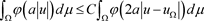
其中
为任一实数,
为Radon测度,
,常数
。
在引理5中,若令
为球体B,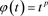 ,
,
,则
演变为
,故而从任一满足
的球体B有
,
,
,则
演变为
,故而从任一满足
的球体B有
(7)
3. 本文主要结论
本节将分别在
和
两种条件下证明有界域上作用于微分形式的复合算子
的局部高阶可积性。
定理1 设
是满足A-调和方程的微分形式,
,
,T为同仑算子,G为Green算子。若
,则复合算子
,且对所有满足
的球体B,存在一不依赖于u的常数C,有
其中
,
为一特定的常数。
证明:(i) 若
,则在球体B上
几乎处处成立,故
为一闭形式,从而
为A-调和方程的解,从而由引理4可得
(8)
其中
,
为一特定常数。
综合式(8)式及引理1的(6)式、引理2知
(9)
其中
。(9)式等价于
(10)
(ii) 若
,则(7)式对
成立,即有
(11)
利用
-空间的单调性及
,可得
(12)
综合引理3、引理1的(5)式、引理2,可得
(13)
综合式(11) (12) (13),便有
(14)
综合式(10) (14)可得:若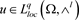 是A-调和方程(4)的解,则
,且
是A-调和方程(4)的解,则
,且
故定理1证毕。
在定理1中,当
时,
,此时p可以充分大,故p可大于q,此时称定理1为复合算子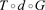 在
条件下的高阶可积性,下面证明在
在
条件下的高阶可积性,下面证明在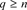 条件下定理仍然成立。
条件下定理仍然成立。
定理2 设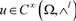 是满足A-调和方程(4)的微分形式,
,
,T为同仑算子,G为Green算子。若
,则复合算子
,且对所有满足
的球体B,存在一不依赖于u的常数C,有
是满足A-调和方程(4)的微分形式,
,
,T为同仑算子,G为Green算子。若
,则复合算子
,且对所有满足
的球体B,存在一不依赖于u的常数C,有
其中
,
为一特定的常数。
证明:(i) 若
,则使用定理1证明(i)中同样的方法可证定理仍然成立。
(ii) 若
,取
,
,由于
,则
,故有
且
。
先后利用引理3、引理1的(5)式、引理2,得
(15)
其中
。利用
-空间的单调性及
,可得
(16)
式(16)等价于
 (17)
(17)
综合式(15) (17),有
(18)
由于
,故(7)式对
成立,于是应用(7)式可得
(19)
经计算可得
,
,综合利用
-空间的单调性及式(18) (19),可得
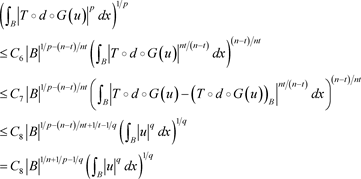 (20)
(20)
式(20)等价于
(21)
式(21)表明:当
时,定理2成立。
综合(i) (ii)可得定理2成立,故定理证毕。
4. 总结
本文证明了
和
两种条件下有界域上作用于微分形式的复合算子
的局部高阶可积性。今后,我们可在基础上进一步研究有界域上相关算子的全局高阶可积性。
基金项目
2021年度江西省教育厅科学技术研究项目“关于调和方程解的高阶可积性理论研究”(编号:GJJ213509)。
参考文献