1. 引言
本文研究中国货币市场短期利率的动态变化规律,首先假设瞬时利率的动态变化用CIR模型来描述。对于不同国家市场的短期利率在CIR模型中的参数值是不同的,所以CIR模型中的参数估计是一类关键的研究问题。关于这类参数估计问题已经有大量的研究工作,例如:Feng和Xie [1] [2] 利用美国和日本的利率数据,在欧拉离散化的基础上使用吉布斯采样对CIR模型进行贝叶斯参数估计;高利翠在文献 [3] 中借助MCMC方法对利率模型CIR过程的参数进行贝叶斯估计;马笑天 [4] 采用贝叶斯估计研究上海同业拆借利率中的隔夜拆借利率;张玉桂等人 [5] 在CIR模型下,使用无损卡尔曼滤波估计方法对Shibor利率数据进行拟合估计;吴恩远在文献 [6] 中对该模型进行加权最小二乘估计,选取上海银行间同业拆放利率(Shibor)得到模型的参数估计值;吴方滢 [7] 利用最小二乘估计解决平稳CIR模型参数估计;王泽峰和刘俊峰 [8] 使用广义矩估计法对一种改进的模型进行估计。在众多文献研究中,最为常见的方法是极大似然估计,其原理在于通过极大化似然函数得到未知参数的估计量(见Valdivieso等 [9] ,Schneider等 [10] ,王素丽等 [11] )。Fergusson等人 [12] 和Kladívko [13] 利用极大似然方法分别对美国现金短期利率和美国的PRIBO3数据进行参数估计。值得注意的是,在对随机过程进行最大似然估计的时候,转移概率密度获取困难,导致无法得到似然函数的显示表达式,因此Aït-Sahali [14] 构造了闭合函数序列、Beskos等人 [15] 利用蒙特卡罗的MLE、Singer [16] 利用卡尔曼滤波提供了转移密度一种数值的近似,从而得到近似的似然函数。文献 [17] 通过实验发现,随着参数的增加,参数估计的准确度急剧下降,当线性随机微分方程的未知参数个数较多时,极大似然估计基本失效,因此齐凤团 [17] 提出了期望方差法用于估计随机微分方程的未知参数,此方法当参数个数较多时表现出了良好的有效性。
中国市场短期利率的种类很多,选取不同的短期利率估计CIR模型的参数时结果会有很大差异。如何选取中国市场短期利率的数据类型,潘冠中 [18] 给出了解决这一问题的两个原则,即相关性原则和成交量最大、选择交易最频繁的利率品种原则;同时根据这两个原则论证了银行间质押式7天回购利率(R007)是瞬时利率的最佳近似代替。
本文利用CIR模型对中国货币市场短期利率建模,模型中的波动项和扩散项均含有未知参数,由于CIR模型中含有三个未知参数,我们采用期望方差法给出参数的估计量,在实证研究中选取R007作为瞬时利率的近似替代,给出中国货币市场短期利率CIR模型的显示表达式,用于刻画利率数据的演化过程,以分析中国货币市场短期利率的动态变化规律。
2. CIR模型及参数估计
2.1. CIR模型及期望方差法
假设
为一个完备的滤子概率空间,{Bt, t ≥ 0}是该空间上的布朗运动,CIR (Cox-Ingersoll-Ross) [19] 模型是描述利率随时间变化的数学模型,具体来说,瞬时利率Xt可用下列随机微分方程来表示:
(1)
其中,
表示短期利率偏长期均衡利率水平的速度,
是长期均衡利率水平,
是描述短期利率过程的瞬时波动率。在实证研究中利用捕捉到的历史利率数据信息对模型的K、b、θ进行准确估计是预测未来利率变化趋势的关键。
本文利用CIR模型对中国货币市场短期利率建模,对于未知参数K、b、θ利用期望方差法进行参数估计。期望方差法的原理是:首先将时间段[0, T]等距划分成N段,每段长度记为h,即ti + 1 − ti = h,i = 0, ∙∙∙, N − 1,由Euler-Maruyama方法将式(1)离散化可得:
利用此差分格式生成Xt的M条轨道;其次在初值处选取一个数据,并在下一个时间点观测到M个数据,即
,
。这样观测一个初值及初值下一个时间点的数据可以提供两个求解方程。由于我们研究的随机微分方程的参数分别是K、b、θ三个,所以需要找到初值的个数为2个,记为
、
,其中
是随机取的一条路径在t1时刻的利率收盘价,
在t2时刻的利率收盘价,建立三个方程。
具体来说,对于从初值
出发的随机微分方程,在t2时刻取M个观测值,记为:
在t2中的M个观测值中任取一个值作为下一时刻t3的初始值,在t3时刻取M个观测值,记为:
对于给定的
,有:
由期望方差法可得:
求解上面三个方程解得参数K、b、θ2的估计量为:
其中
2.2. 算例
为了验证期望方差法给出估计量的准确性,本小节在CIR模型当中将参数真实值分别设为K = 0.21459,b = 0.08579,θ = 0.07830,X0 = 0.1 (见Fan and Zhang, 2003 [20] )。利用蒙特卡洛模拟方法生成Xt的100条轨道(如图1)。

Figure 1. Curve graph of 100 paths of CIR model
图1. CIR模型的100条轨道曲线图
利用构造的统计量
,反向估计K、b、θ,并与真实值对比误差。下面给出具体算法步骤,见表1。

Table 1. Numerical estimation algorithm for parameters in the CIR model
表1. CIR模型中估计量的数值算法
由参数
的表达式可以看出,参数值随着取值不同初始时刻,其结果是不一样的。假设
取坐标第19时刻的100维数据里面中的任意一个,
取坐标第20时刻的100维数据,将
的100维数据随机选取一个数值当作t3时刻的初始值,
是坐标第21时刻的100维数据,这里t2 − t2 = h = 1。将上面得到的数据执行表1中的步骤4,得到模拟值随着时间取值变化的误差值,见表2。

Table 2. Simulated values and error results of parameters
表2. 参数的模拟值及误差结果
数值结果显示:当取值时刻在横坐标轴上较大时,利用期望方差法得到的CIR中的参数估计值与真实假设值越接近,模拟值与真实值之间的误差项越小,因此验证期望方差法的可行性。
3. 实证研究

Figure 2. R007 interest rate sequence diagram
图2. R007利率时序图
中国市场短期利率有很多种类型,用哪一种类型利率作为中国瞬时利率的最佳替代是实证研究的一类重要问题。潘冠中 [18] 给出了解决这一问题的两个原则,即相关性原则和成交量最大、选择交易最频繁的利率品种原则;同时根据这两个原则论证了银行间质押式7天回购利率(R007)是瞬时利率的最佳近似代替。本文选择交易1个月到期收益率近似R007利率作为样本,时间从1999年6月17日到2023年6月25日,总的数据容量为6000。数据来源于Wind数据库,相应的时间步长为1 (单位为:天),运行环境在Anaconda3中的Jupyter notebook,图2给出了利率收盘价随时间的变化曲线。
对图2每间隔50个数据作为一组,得到120条曲线,如图3所示。
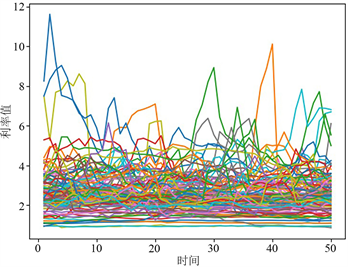
Figure 3. 120 interest rate curve graphs
图3. 120条利率曲线图
在该实例中,
可以取到0到49的任意一个时刻,假设
取坐标第19时刻的120维数据里面中的任意一个,其中t2 − t2 = h = 1,则
代表横坐标第20的120维数据里面中的全部数据。将得到的离散数据带入CIR模型的参数估计量,可得参数K、b、θ的估计值见表3。

Table 3. Parameter estimation values in the CIR model
表3. CIR模型中的参数估计值
则中国市场短期利率CIR模型显示表达式为:
(2)
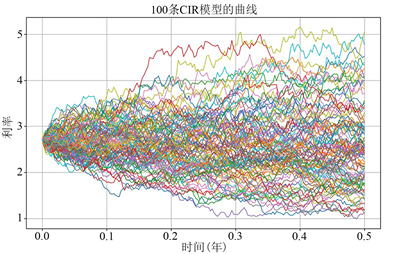
Figure 4. Simulate 100 curves for Equation (2)
图4. 对(2)式模拟100条曲线
也就是说,在1999年6月17日到2023年6月25日期间,中国市场短期利率偏长期均衡利率水平的速度为0.1618,中国货币市场的长期均衡利率水平为0.99324,中国短期利率过程的瞬时波动率为0.7818。最后我们用python画出方程(2)的100条样本轨道,刻画中国货币市场短期利率的动态变化规律。其中把1999年6月17日的利率收盘价数据作为初始值X0 = 2.7,n = 180,T = 0.5 (代表半年),其n为[0, T]的划分份数,
代表每间隔一天,对(2)式模拟100条曲线如图4所示。
4. 结论
本文采用CIR模型来描述中国货币市场短期利率的动态特征,使用期望方差法对CIR模型进行参数估计。随着随机微分方程参数个数的增加,经典的极大似然估计方法估计效果明显下降。期望方差法可以提高随机微分方程参数估计的准确性。进一步,利用蒙特卡洛模拟方法得到CIR模型的估计值随着时刻变大收敛到参数真实值,从实验角度验证了估计量的准确性。最后实证分析,选取银行间质押式7天回购利率(R007)近似代替瞬时利率作为样本数据,得到CIR模型的显示表达式,从而描述出中国货币市场利率的动态变化规律。
基金项目
辽宁省自然科学基金指导计划项目(2019-ZD-0087)。
NOTES
*通讯作者。