1. 引言
当今社会,培养什么人、怎样培养人、为谁培养人称为中国高等教育必须回答的根本问题。高校应将思政教育融入到各类课程中,强化课程思政功能。这需要通过课程设计和教学实践,加强学科知识和思想道德教育的有机结合,使学生能够在学科知识学习的同时,获得全面的人文素养和价值观念 [1] 。在素质教育全面发展的今天,高校的理科专业需要逐渐树立起价值塑造、能力培养、知识传授三位一体的教学目标。专业课程的每个细节,都可融入对学生的价值引领。“大学课程不仅仅是追问其范围的解释之学,更是规范人的价值之学”。高校各类课程的知识传授与价值观教育必须同频共振。
解析几何是构架数与形,代数与几何的桥梁,是数学专业课的基石。曲线是解析几何研究的主要对象之一,求曲线的轨迹方程是解析几何的基本问题之一,也是众多科学领域如轨道交通、天体运行轨道、原子轨道等研究的基础。旋轮线是典型的平面曲线之一,它具有最速降线性质和等时性,实用性极其广泛。
2. 教材分析
旋轮线是教材第二章第一节平面曲线内容。平面曲线研究是空间曲线研究的基础,也是研究各类曲面性质的基础。教材核心内容聚焦在两个方面:一是建立动点运动的轨迹方程,特别是建立向量式和坐标式参数方程,借助参数的变化反应动点位置的变化;二是参数方程与一般方程间的转化,注意转化前后方程的等价性,真正体现曲线参数方程是解析几何联系实际的一个重要工具。
3. 学情分析
学生已经掌握了平面曲线中较为简单的圆锥曲线的标准方程,也了解了圆锥曲线的参数方程形式,为进一步学习较为复杂的旋轮线方程奠定了基础。但面对具体的实际问题,学生分析问题、研究问题、解决问题的能力不足,需要在教师的引领下进行系统深入的学习,数学思维能力需进一步的提升。
4. 课程思政理念下教学与育人目标
知识传授目标:掌握曲线参数方程建立的思想和步骤;理解一般方程、参数方程间的区别与联系,掌握两类方程间的互化。
1) 通过建立坐标系,搭建曲线与方程的联系,追根索源,品古鉴今,培养学生优秀品格,严谨的科学态度,刻苦钻研的精神,学会透过现象看本质。
2) 通过动态几何画板Geogebra (以下简称GGB)绘制旋轮线图象,激发学生的学习兴趣,丰富学生的直观感知,培养学生运用信息技术的能力。
3) 通过将曲线参数方程转化为一般方程,虽然方程形式发生了变化,但其本质不变。引导学生运用敏锐的观察力、辨析力去发现事件中的变与不变。
4) 曲线图象等所呈现出了数学的简洁美、和谐美,体会数学不但拥有真理,而且拥有至高的美提升学生感受美、鉴赏美、表现美、创造美的能力。
5) 通过旋轮线在日常生活及物理中的广泛应用,将理论与实际相结合,培养学生的创新意识和应用意识。
5. 教学重难点
旋轮线教学重点:建立旋轮线参数方程的步骤;建立轨迹方程的思想方法;曲线参数方程与一般方程间的相互转化。
旋轮线教学难点:如何选取恰当的坐标系和参数才能高效解决轨迹问题。
6. 课程思政理念下的教学设计与实践
6.1. 教学策略
采用启发式教学原则设置情景导入,借助信息技术教学以及讨论、演示、实验等多元教学法进行教学,注重数学思想方法的渗透,注重数与形的融合,注重知识传授与价值引领的同频共振。
6.2. 课程思政教学实施过程设计
(1) 实例导入
1) 钟摆——惠更斯等时摆
意大利科学家伽利略曾用自行制的滴漏来做单摆的试验,证明了单摆摆动的时间跟摆幅没有关系,只跟单摆摆线的长度有关.这个现象使伽利略想到或许可以利用单摆来制作精确的时钟。伽利略的发现振奋了科学界,过了不久,荷兰科学家惠更斯决定要做出一个精确的时钟来。伽利略的单摆是在一段圆弧上摆动的,所以我们也叫做圆周摆,而惠更斯想要找出一条曲线,使摆沿着这样的曲线摆动时,摆动周期完全与摆幅无关,他纯粹往数学曲线上去研究,经过不少次的失败,这样的曲线终于找到了,数学上把这种曲线叫做“摆线”,“等时曲线”或“旋轮线”。
2) 古建筑屋顶
古代宫廷建筑中特殊的屋顶建筑,屋顶从侧面看呈两条曲线,加上屋檐上翘,不仅看起来雄壮威严,更重要的是这样的设计使得屋顶上的雨水能以最快的速度流走,提高了建筑物的安全性。
3) 盘旋的“过山车”
大型游乐场,盘旋而又跌宕起伏的过山车轨道,设计时利用了特殊的曲线在垂直下降时达到最高时速度的性质,使得挑战者能享受到最佳的刺激体验。
[设计意图]为追求科学的真谛,探索真理的道路很艰辛,经历不断失败与挫折,不断实践。通过数学文化的渗透,培养学生的兴趣、善思、坚持与执着。
(2) 问题提出
[问题1]
小时候喜欢玩的滚环及自行车、马车、汽车、火车等的车轮上点随车辆前进时的运动轨迹是什么曲线呢?我们可以从众多具体问题中抽象出数学问题:一个圆在一直线上无滑动地滚动,求圆周上一点的轨迹。
[问题2]有趣现象:火车悖论。
在任一瞬间,一辆移动的火车不可能整个都朝机车拖动的方向移动,火车上总有一部分是朝火车运动的相反方向移动。这是怎么回事呢?
[设计意图]理论与实际相结合,透过现象看本质,联系科学发展史,激发起学生的学习兴趣,而且寓教于乐,有思想教育意义。
(3) 实验探究
1) 平面曲线方程
定义1 [2] 当平面上取定了坐标系之后,如果一个方程与一条曲线之间有着关系:
① 满足方程的
必是曲线上某一点的坐标(完备性);
② 曲线上任何一点的坐标
满足这个方程(纯粹性),
那么这个方程就叫做这条曲线的方程,这条曲线叫做这个方程的图形。
,或
定义2 [2] 在坐标系
下,向量函数
(
)叫做曲线的向量式参数方程。
曲线的坐标式参数方程:
消去参数,可将参数方程转化为一般方程。
2) 旋轮线方程建立
向量函数曲线属于“形”的范畴,方程则属于“数”的范畴,借助直角坐标系将二者联系在一起。曲线方程的学习是从学生已学知识为切入点,引起学生关注,引发数学思考,鼓励学生发现数学的规律和问题解决的途径。
[问题3]一个圆无滑动地沿一条直线滚动时,其圆周上一点运动的轨迹为旋轮线(见图1)。
建立如图1的直角坐标系,直线为x轴,以圆与x轴相切的点为坐标原点O,过O设作x轴的垂线为y轴。
设圆的半径为a,开始时动点在原点。经过一段时间以后,动点到达图中P点位置,此时切点为A,圆心移到了C点。动点P的向径为:
设
,于是
,有
,故曲线向量式参数
方程为:
坐标式参数方程为:
消去参数得一般方程:
借助GGB绘制动点的运动轨迹,并观察随着圆的半径增大或减少时轨迹发生了怎样的变化,小结旋轮线的主要性质。
[设计意图]使学生不断地经历直观感知、观察发现、归纳类比、空间想象、抽象概括、反思与建构等思维过程。
方程的曲线和曲线的方程,数形结合达到高度、巧妙、和谐的统一。通过观察图形,分析变与不变,提高自身分辨能力,分析问题,探究问题的能力。“动”与“静”的辩证思维正是分析和解决轨迹问题的重要思路,这可以帮助学生对曲线与方程的深刻理解 [3] 。
总结曲线轨迹方程建立的步骤(四步法):建立直角坐标系,选设适当的参数,表出动点的径矢,写出向量式参数方程和坐标式参数方程。四步法适用于所有轨迹问题的求解,包含平面上或空间上点的轨迹问题,也包含空间曲线轨迹问题等,核心思想就是选取一个参数将动点的向径表示出来。
[设计意图]参数选取对于建立参数方程非常重要。参数选取不同,对应曲线的参数方程就会不同。轨迹方程建立中参数的选取要恰当。曲线参数个数通常是一个,若选择了两个,一定要找到彼此的联系。对于同一条轨迹,方程形式不同,但本质相同。透过现象看本质。生活中要学会用敏锐的眼光去发现事物的本质。
借助GGB动态软件进行数学实验演示,展示该曲面方程对应的图象,并演示动点在不同时刻的位置,即曲面图象变化的动态过程(GIF格式展示)。数学实验法在解析空间几何教学中的具体应用,以实现数学教学的路径创新 [4] 。
3) 内(外)旋轮线方程建立
[问题4]一个小圆在一个大圆内无滑动地滚动,求小圆上一点的轨迹(见图2)。
开始时动点P与A重合,建立如图的直角坐标系,请同学们尝试将动点P的径矢写成几个易表示出的向量之和。
如图向量
,或
,或
,思考哪种分解表示形式更恰当。
适当选取参数
,将所需表示的向量表示出来,并找寻
的关系,使得建立该轨迹曲线方程独立参数为一个。
[设计意图]提高学生的辨析力,寻求适于解决问题的方式方法。引导学生在自己人生路上的岔路口时,需要明确目标,分析思考选择适合于自己强行的路。
合理建立坐标系并选取参数易求得内旋轮线坐标式参数方程为:
实验1:请用数学软件绘制
(m为正数时,
)对应的内旋轮线图象(见图3)。
实验2:请用数学软件绘制
(
为互质的正数,
)对应的内旋轮线图象(见图4)。
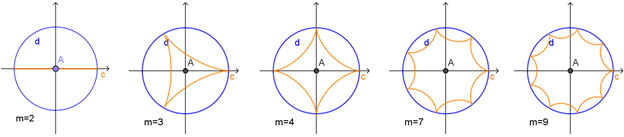
Figure 3. Hypotrochoid when a equals mb
图3. 内旋轮线(
)

Figure 4. Hypotrochoid when a equals
图4. 内旋轮线 (
)
分组设计图象并分享,并归纳整理
变化时,图象的变与不变因素。
[设计意图]由特殊到一般,从简单到复杂,使新知识的建构顺畅和自然,既体现在教师引导下学生自我建构,又使学生感到知识之间并不是孤立的,而是一个相互联系密切相关的整体。该实验探究能够提升学生的创新能力和应用意识。
类比进行外旋轮线方程建立及图象绘制,观察图象之特点(由学生自己完成),特别当
时,该旋轮线称为心脏线。
注1:注重了教师引导、渗透了类比思想,提升了学生数学素养。
注2:通过教学过程中的方程、图形、变换等让学生感受了数学的思想之美,方法之美,形式之美。教学各环节中不断渗透美育,提升学生审美能力,同时激发了学生探索轨迹问题的积极性。
(4) 拓展迁移
1) 变幅旋轮线
回到火车悖论问题,从实际问题抽象出相应的数学问题是:平面上半径为r的动圆K在直线上滑动地滚动时,动点M的运动轨迹问题。设点M到动圆心的距离为l,当l > r时为长幅旋轮线(见图5);当l < r时为短幅圆内旋轮线。
长幅旋轮线、长幅内外旋轮线及短幅内外旋轮线都有实际的应用。如内外旋轮线在机械设计、理论力学等方面应用广泛,如行星搅拌机,内啮合、外啮合型定轴轮系等。
2) 广义旋轮线
一条光滑曲线在另一条光滑曲线上无滑动滚动,滚动曲线上一点的轨迹就是广义旋轮线。我们建立参数方程时,需选用自然参数(弧长),写出广义旋轮线的轨迹方程;利用数学软件,可以把椭圆旋轮线画出,并进行做动画演示。
[设计意图]引导学生合理地应用知识,进而发展学生的应用意识,培养学生热爱数学,科技兴国,铸就强国梦的理想信念。让学生感悟数学与生活息息相关,用数学的眼光观察世界,用数学的思维分析世界,用数学的语言表达世界。
7. 课程思政教学实施成效
通过三个实例导入研究对象,激发兴趣,让学生经历将实际问题抽象成数学模型并进行解释和应用的过程。提出问题,使思维目标集中,培养学生良好的思维习惯,学生能够在教师引导下主动思考问题解决方法。通过交流讨论、实验探究等方式,提升了学生观察能力、抽象概括能力及创新能力。强化类比、联想的方法,领会到了解决轨迹问题的核心思想。迁移拓展环节使学生对知识进行了再认识与提高,培养了学生知识迁移与应用的能力。
总之,整个教学设计充分体现了知识传授与课程思政的有效融合。学生在教师引领下不仅能够掌握旋轮线的性质及方程建立方法,而且学生可通过“建、设、表、写”四步法解决所有的轨迹问题,学生发现问题、分析问题、解决问题的能力得到了提升。凝练思政元素,以实践为契机创新教学方法,可以很好地提高课堂教学质量,提高育人效果。
基金项目
太原师范学院2022年度教学改革项目“师范院校《高等数学》三位一体的教学改革研究(课题编号:JGLX2233)”。