七次广义Ball曲线的两种扩展

Two Extensions of Generalized Ball Curves of Seventh Degree

摘要: 构造了两组含形状参数的多项式基函数：第一组基既是七次Wang-Ball基的扩展，又是七次Said-Ball基的扩展；第二组基既是七次Said-Ball基的扩展，又是七次Bernstein基的扩展。并由此定义了两种新的七次广义Ball曲线：前者不仅包括了七次Wang-Ball和Said-Ball曲线，还涵盖了无数条处于这两种曲线之间的曲线；后者不仅包括了七次Said-Ball和Bézier曲线，还涵盖了无数条处于这两种曲线之间的曲线。依次分析了两种新的广义Ball曲线与七次Bézier曲线之间的关系后明确了每个形状参数的几何意义，并给出了其几何作图法。

Abstract: Two classes of polynomial basis functions with shape parameter are constructed. The first class of basis is not only the extension of Wang-Ball basis of seventh degree, but also the extension of Said-Ball basis of seventh degree. The second class of basis is not only the extension of Said-Ball ba-sis of seventh degree, but also the extension of Bernstein basis of seventh degree. Based on these two new bases, two classes of new generalized Ball curves of seventh degree are defined. The former contained the Wang-Ball and Said-Ball curve of seventh degree and many curves between them. The latter contained the Said-Ball and Bézier curve of seventh degree and many curves between them. After analyzing the relationship between new generalized Ball curves and the Bezier curve of seventh degree, the geometric meaning of each shape parameter is clarified, and its geometric drawing method is given.

1. 引言

数学家Ball [1] [2] [3] 提出了三次参数曲线，随后广义Ball曲线曲面的研究工作不断推进并且取得众多成果。王国瑾 [4] 将三次参数曲线推广至n次广义Ball曲线并分析了其几何性质。Said [5] 提出了一种的新的广义Ball曲线，将三次参数曲线推广至任意奇数次。在文献 [6] 中，文献 [4] [5] 中的曲线分别被称为Wang-Ball和Said-Ball曲线，并通过比较分析发现Wang-Ball曲线的递归算法效率优于Bézier曲线和Said-Ball曲线。与同次Bézier曲线相比，广义Ball曲线在曲线求值和升降阶等计算方面更高效。因此，广义Ball曲线被广泛应用于几何制造业。

文献 [7] [8] 构造了两种带位置参数的广义Ball曲线。从提高t的次数的设计思路出发，文献 [9] 先构造了一组新的含形状参数 $\lambda$ 的基函数，再由此构造了与三次Ball曲线性质相似的扩展曲线。文献 [10] 提出了两种四次广义Ball曲线的生成方法。文献 [11] 先构造了次数分别为三次和四次的带形状参数的基函数，再基于这两组基函数定义了两种不同的扩展三次Ball曲线。文献 [9] [12] [13] 讨论了广义Ball曲线间的拼接问题，其中，文献 [13] 还给出了 $G^1$ 连续条件下形状参数的选取准则。

整合文献 [7] [8] [9] 的思想，本文依次构造了 $\alpha B$ 和 $\beta B$ 基函数，其中， $\alpha B$ 基函数可以从七次Wang-Ball基过渡到Said-Ball基，而 $\beta B$ 基函数可以从七次Said-Ball基过渡到Bernstein基。基于 $\alpha B$ 基函数和 $\beta B$ 基函数构造的曲线均具有形状可调性，当 $\alpha B$ 曲线中的形状参数 $\alpha$ 取不同值时，不仅可以得到七次Wang-Ball与Said-Ball曲线，而且还可以得到无数条处于这两种曲线之间的曲线；当 $\beta B$ 曲线中的形状参数 $\beta$ 取不同值时，不仅可以得到七次Said-Ball与Bézier曲线，而且还可以得到无数条处于这两种曲线之间的曲线。

2. 介于Wang-Ball和Said-Ball曲线之间的曲线

2.1. 基函数的构造与性质

定义1 对 $\forall t\in \left[0,1\right]$ 和 $\alpha \in \left[0,1\right]$ ，多项式

$\{\begin{array}{l}{b}_{0,7}\left(t\right)=\left(1-2\alpha t+\alpha t^2\right){\left(1-t\right)}^2\\ b_{1,7}\left(t\right)=\left(2+2\alpha -4\alpha t\right)t{\left(1-t\right)}^3\\ b_{2,7}\left(t\right)=\left(4+6\alpha \right)t^2{\left(1-t\right)}^4\\ b_{3,7}\left(t\right)=\left(8+12\alpha \right)t^3{\left(1-t\right)}^4\\ b_{4,7}\left(t\right)=\left(8+12\alpha \right)t^4{\left(1-t\right)}^3\\ b_{5,7}\left(t\right)=\left(4+6\alpha \right)t^4{\left(1-t\right)}^2\\ b_{6,7}\left(t\right)=\left(2-2\alpha +4\alpha t\right)t^3\left(1-t\right)\\ b_{7,7}\left(t\right)=\left(1-\alpha +\alpha t^2\right)t^2\end{array}$ (1)

被称为含形状参数 $\alpha$ 的七次广义Ball基函数，即 $\alpha B$ 基。

$\alpha B$ 基具有如下性质：

性质1 非负性，即 $b_{i,7}\left(t\right)\ge 0\left(i=0,1,\cdots ,7\right)$ 。

性质2 规范性，即 ${\displaystyle \underset{i=0}{\overset{7}{\sum }}{b}_{i,7}\left(t\right)}=1$ 。

性质3 对称性，即 $b_{i,7}\left(t\right)=b_{7-i,7}\left(1-t\right),i=0,1,\cdots ,7$ 。

性质4 端点性质：

$\{\begin{array}{l}{b}_{0,7}\left(0\right)=1\\ b_{i,7}\left(0\right)=0,i=1,2,\cdots ,7\end{array};\{\begin{array}{l}{b}_{i,7}\left(1\right)=0,i=0,1,\cdots ,6\\ b_{7,7}\left(1\right)=1\end{array};$

$\{\begin{array}{l}{b^{\prime }}_{0,7}\left(0\right)=-\left(2\alpha +2\right)\\ {b^{\prime }}_{1,7}\left(0\right)=2\alpha +2\\ {b^{\prime }}_{i,7}\left(0\right)=0,i=2,3,4,5,6,7\end{array};\{\begin{array}{l}{b^{\prime }}_{i,7}\left(1\right)=0,i=0,1,2,3,4,5\\ {b^{\prime }}_{6,7}\left(1\right)=-\left(2\alpha +2\right)\\ {b^{\prime }}_{7,7}\left(1\right)=2\alpha +2\end{array}.$

性质5 单峰性，即每个基函数在定义域 $\left[0,1\right]$ 上有唯一的最大值。

性质6 退化性：当 $\alpha =0$ 时， $\alpha B$ 基是七次Wang-Ball基；当 $\alpha =1$ 时， $\alpha B$ 基是七次Said-Ball基。

2.2. 曲线的构造与性质

定义2 给定一组控制顶点 $P_i\in R^d\left(d=2,3;i=0,1,\cdots ,7\right)$ ，对 $\forall t\in \left[0,1\right]$ ，曲线

$p\left(t\right)={\displaystyle \underset{i=0}{\overset{7}{\sum }}{P}_i}{b}_{i,7}\left(t\right)$ (2)

被称为含形状参数 $\alpha$ 的七次广义Ball曲线，即 $\alpha B$ 曲线。

根据 $\alpha B$ 基的性质可以得到， $\alpha B$ 曲线具有下列性质：

性质1 端点性质：

$\{\begin{array}{c}p\left(0\right)=P_0\\ p\left(1\right)=P_7\end{array};\{\begin{array}{c}{p}^{\prime }\left(0\right)=\left(2\alpha +2\right)\left(P_1-P_0\right)\\ p^{\prime }\left(1\right)=\left(2\alpha +2\right)\left(P_7-P_6\right)\end{array}$ 。

性质2 凸包性。由 $\alpha B$ 基的非负性与规范性可以推出， $\alpha B$ 曲线始终会位于其控制多边形构成的凸包内。

性质3 对称性，即不论是控制多边形 $P_0{P}_1\cdots P_7$ 还是 $P_7{P}_6\cdots P_0$ 构成的 $\alpha B$ 曲线形状相同仅方向相反。

性质4 几何不变性与仿射不变性，即 $\alpha B$ 曲线的形状不会随着坐标系的不同而变化，并且不论是对 $\alpha B$ 曲线的控制多边形进行仿射变换还是对 $\alpha B$ 曲线直接进行仿射变换，两者所对应的新曲线仍然相同。

2.3. 形状参数的几何意义

形状参数 $\alpha$ 的取值变化会直接影响 $\alpha B$ 曲线形状，下面先讨论 $\alpha B$ 曲线中参数 $\alpha$ 的几何意义。 $\alpha B$ 基可转化为七次Bernstein基函数的线性组合形式，即

$\{\begin{array}{l}{b}_{0,7}\left(t\right)=B_{0,7}\left(t\right)+\frac{5-2\alpha }{7}{B}_{1,7}\left(t\right)+\frac{10-7\alpha }{21}{B}_{2,7}\left(t\right)+\frac{10-9\alpha }{35}{B}_{3,7}\left(t\right)+\frac{5-5\alpha }{35}{B}_{4,7}\left(t\right)+\frac{1-\alpha }{21}{B}_{5,7}\left(t\right)\\ b_{1,7}\left(t\right)=\frac{2+2\alpha }{7}{B}_{1,7}\left(t\right)+\frac{6+2\alpha }{21}{B}_{2,7}\left(t\right)+\frac{6-2\alpha }{35}{B}_{3,7}\left(t\right)+\frac{2-2\alpha }{35}{B}_{4,7}\left(t\right)\\ b_{2,7}\left(t\right)=\frac{4+6\alpha }{21}{B}_{2,7}\left(t\right)+\frac{4+6\alpha }{35}{B}_{3,7}\left(t\right)\\ b_{3,7}\left(t\right)=\frac{8+12\alpha }{35}{B}_{3,7}\left(t\right)\\ b_{4,7}\left(t\right)=\frac{8+12\alpha }{35}{B}_{4,7}\left(t\right)\\ b_{5,7}\left(t\right)=\frac{4+6\alpha }{35}{B}_{4,7}\left(t\right)+\frac{4+6\alpha }{21}{B}_{5,7}\left(t\right)\\ b_{6,7}\left(t\right)=\frac{2-2\alpha }{35}{B}_{3,7}\left(t\right)+\frac{6-2\alpha }{35}{B}_{4,7}\left(t\right)+\frac{6+2\alpha }{21}{B}_{5,7}\left(t\right)+\frac{2+2\alpha }{7}{B}_{6,7}\left(t\right)\\ b_{7,7}\left(t\right)=\frac{1-\alpha }{21}{B}_{2,7}\left(t\right)+\frac{5-5\alpha }{35}{B}_{3,7}\left(t\right)+\frac{10-9\alpha }{35}{B}_{4,7}\left(t\right)+\frac{10-7\alpha }{21}{B}_{5,7}\left(t\right)+\frac{5-2\alpha }{7}{B}_{6,7}\left(t\right)+B_{7,7}\left(t\right)\end{array}$ (3)

记作

$b=MB$

其中

$b={\left(\begin{array}{cccc}{b}_{0,7}\left(t\right)& b_{1,7}\left(t\right)& \cdots & b_{7,7}\left(t\right)\end{array}\right)}^{\text{T}}$ ，

$M=\left(\begin{array}{cccccccc}1& \frac{5-2\alpha }{7}& \frac{10-7\alpha }{21}& \frac{10-9\alpha }{35}& \frac{5-5\alpha }{35}& \frac{1-\alpha }{21}& 0& 0\\ 0& \frac{2+2\alpha }{7}& \frac{6+2\alpha }{21}& \frac{6-2\alpha }{35}& \frac{2-2\alpha }{35}& 0& 0& 0\\ 0& 0& \frac{4+6\alpha }{21}& \frac{4+6\alpha }{35}& 0& 0& 0& 0\\ 0& 0& 0& \frac{8+12\alpha }{35}& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{8+12\alpha }{35}& 0& 0& 0\\ 0& 0& 0& 0& \frac{4+6\alpha }{35}& \frac{4+6\alpha }{21}& 0& 0\\ 0& 0& 0& \frac{2-2\alpha }{35}& \frac{6-2\alpha }{35}& \frac{6+2\alpha }{21}& \frac{2+2\alpha }{7}& 0\\ 0& 0& \frac{1-\alpha }{21}& \frac{5-5\alpha }{35}& \frac{10-9\alpha }{35}& \frac{10-7\alpha }{21}& \frac{5-2\alpha }{7}& 1\end{array}\right)$ ，

$B={\left(\begin{array}{cccc}{B}_{0,7}\left(t\right)& B_{1,7}\left(t\right)& \cdots & B_{7,7}\left(t\right)\end{array}\right)}^{\text{T}}$ 。

如果令

$P=\left(\begin{array}{cccc}{P}_0& P_1& \cdots & P_7\end{array}\right)$

则式(2)的等价表示为

$p\left(t\right)=PMB$ (4)

将七次Bézier曲线的控制顶点记作 $V_i\left(i=0,1,\cdots ,7\right)$ ，再令

$V=\left(\begin{array}{cccc}{V}_0& V_1& \cdots & V_7\end{array}\right)$

则可用七次Bézier曲线等价表示 $\alpha B$ 曲线为

$p\left(t\right)=VB$ (5)

比较式(4)和式(5)可得

$V=PM$ (6)

即

$\{\begin{array}{l}{V}_0=P_0\\ V_1=\frac{5-2\alpha }{7}{P}_0+\frac{2+2\alpha }{7}{P}_1\\ V_2=\frac{10-7\alpha }{21}{P}_0+\frac{6+2\alpha }{21}{P}_1+\frac{4+6\alpha }{21}{P}_2+\frac{1-\alpha }{21}{P}_7\\ V_3=\frac{10-9\alpha }{35}{P}_0+\frac{6-2\alpha }{35}{P}_1+\frac{4+6\alpha }{35}{P}_2+\frac{8+12\alpha }{35}{P}_3+\frac{2-2\alpha }{35}{P}_6+\frac{5-5\alpha }{35}{P}_7\\ V_4=\frac{5-5\alpha }{35}{P}_0+\frac{2-2\alpha }{35}{P}_1+\frac{8+12\alpha }{35}{P}_4+\frac{4+6\alpha }{35}{P}_5+\frac{6-2\alpha }{35}{P}_6+\frac{10-9\alpha }{35}{P}_7\\ V_5=\frac{1-\alpha }{21}{P}_0+\frac{4+6\alpha }{21}{P}_5+\frac{6+2\alpha }{21}{P}_6+\frac{10-7\alpha }{21}{P}_7\\ V_6=\frac{2+2\alpha }{7}{P}_6+\frac{5-2\alpha }{7}{P}_7\\ V_7=P_7\end{array}$ (7)

形状参数 $\alpha$ 的几何解释：由式(7)可知， $P_0{V}_1:V_1{P}_1=2+2\alpha :5-2\alpha$ ， $P_6{V}_6:V_6{P}_7=5-2\alpha :2+2\alpha$ 。当 $\alpha =1$ 时，如图1所示， $\alpha B$ 曲线的控制多边形为 $P_0{P}_1\cdots P_7$ ，与 $\alpha B$ 曲线等价的Bézier曲线的控制多边形为 $V_0{V}_1\cdots V_7$ 。

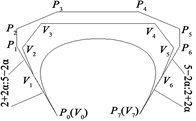
Figure 1. The geometric meaning of shape parameter $\alpha$

图1. 形状参数 $\alpha$ 的几何解释

2.4. 形状参数对曲线形状的影响

由2.3节可知，当 $\alpha$ 增大时，与 $\alpha B$ 曲线等价的七次Bézier曲线的控制多边形将会不断逼近 $\alpha B$ 曲线的控制多边形。同时由Bézier曲线的逼近性可知，当 $\alpha$ 增大时， $\alpha B$ 曲线也会随之不断逼近其控制多边形。图2中依次取 $\alpha =0,\frac{1}{4},\frac{1}{2},\frac{3}{4},1$ 生成曲线1~5，其中，曲线1和5分别为由 $P_0{P}_1\cdots P_7$ 所定义的七次Wang-Ball曲线与Said-Ball曲线。

2.5. 曲线的几何作图法

通过2.3节的分析可知， $\alpha B$ 曲线可以转化为七次Bézier曲线，而且式(7)明确了两者控制顶点之间的显性关系。所以当 $\alpha B$ 曲线的控制顶点已知时，可以先利用式(7)求解其相对应的七次Bézier曲线的控

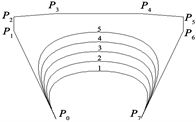
Figure 2. $\alpha B$ curves with different values of $\alpha$

图2. $\alpha$ 不同取值时的 $\alpha B$ 曲线

制顶点，再根据Bézier曲线的几何作图法，由七级递推后得到的最后一点即为 $\alpha B$ 曲线上的点。令 $\alpha =1$ 且 $t=\frac{1}{2}$ ，如图3所示， $P_0{P}_1\cdots P_7$ 为 $\alpha B$ 曲线的控制多边形，则该 $\alpha B$ 曲线对应的七次Bézier曲线的控制多边形为 $V_0{V}_1\cdots V_7$ 。

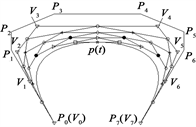
Figure 3. The geometric drawing method of $\alpha B$ curves

图3. $\alpha B$ 曲线的几何作图法

3. 介于Said-Ball和Bézier曲线之间的曲线

3.1. 基函数的构造与性质

定义3 对 $\forall t\in \left[0,1\right]$ 和 $\beta \in \left[0,1\right]$ ，多项式

$\{\begin{array}{l}{c}_{0,7}\left(t\right)=\left(1-3\beta t+3\beta t^2-\beta t^3\right){\left(1-t\right)}^4\\ c_{1,7}\left(t\right)=\left(4+3\beta -14\beta t+7\beta t^2\right)t{\left(1-t\right)}^4\\ c_{2,7}\left(t\right)=\left(10+11\beta -21\beta t\right)t^2{\left(1-t\right)}^4\\ c_{3,7}\left(t\right)=\left(20+15\beta \right)t^3{\left(1-t\right)}^4\\ c_{4,7}\left(t\right)=\left(20+15\beta \right)t^4{\left(1-t\right)}^3\\ c_{5,7}\left(t\right)=\left(10-10\beta +21\beta t\right)t^4{\left(1-t\right)}^2\\ c_{6,7}\left(t\right)=\left(4-4\beta +7\beta t^2\right)t^4\left(1-t\right)\\ c_{7,7}\left(t\right)=\left(1-\beta +\beta t^3\right)t^4\end{array}$ (8)

被称为含形状参数 $\beta$ 的七次广义Ball基函数，即 $\beta B$ 基。

$\beta B$ 基具有如下性质：

性质1 非负性，即 $c_{i,7}\left(t\right)\ge 0\left(i=0,1,\cdots ,7\right)$ 。

性质2 规范性，即 ${\displaystyle \underset{i=0}{\overset{7}{\sum }}{c}_{i,7}\left(t\right)}=1$ 。

性质3 对称性，即 $c_{i,7}\left(t\right)=c_{7-i,7}\left(1-t\right),i=0,1,\cdots ,7$ 。

性质4 端点性质：

$\{\begin{array}{l}{c}_{0,7}\left(0\right)=1\\ c_{i,7}\left(0\right)=0,i=1,2,\cdots ,7\end{array};\{\begin{array}{l}{c}_{i,7}\left(1\right)=0,i=0,1,\cdots ,6\\ c_{7,7}\left(1\right)=1\end{array};$

$\{\begin{array}{l}{c^{\prime }}_{0,7}\left(0\right)=-\left(3\beta +4\right)\\ {c^{\prime }}_{1,7}\left(0\right)=3\beta +4\\ {c^{\prime }}_{i,7}\left(0\right)=0,i=2,3,4,5,6,7\end{array};\{\begin{array}{l}{c^{\prime }}_{i,7}\left(1\right)=0,i=0,1,2,3,4,5\\ {c^{\prime }}_{6,7}\left(1\right)=-\left(3\beta +4\right)\\ {c^{\prime }}_{7,7}\left(1\right)=3\beta +4\end{array}.$

性质5 单峰性，即每个基函数在定义域 $\left[0,1\right]$ 上有唯一最大值。

性质6 退化性：当 $\beta =0$ 时， $\beta B$ 基是七次Said-Ball基；当 $\beta =1$ 时， $\beta B$ 基是七次Bernstein基。

3.2. 曲线的构造与性质

定义4 给定一组控制顶点 $Q_i\in R^d\left(d=2,3;i=0,1,\cdots ,7\right)$ ，对 $\forall t\in \left[0,1\right]$ ，曲线

$q\left(t\right)={\displaystyle \underset{i=0}{\overset{7}{\sum }}{Q}_i}{c}_{i,7}\left(t\right)$ (9)

被称为含形状参数 $\beta$ 的七次广义Ball曲线，即 $\beta B$ 曲线。

类似于 $\alpha B$ 曲线性质， $\beta B$ 曲线具备下列性质：

性质1 端点性质：

$\{\begin{array}{c}q\left(0\right)=Q_0\\ q\left(1\right)=Q_7\end{array};\{\begin{array}{c}{q}^{\prime }\left(0\right)=\left(3\beta +4\right)\left(Q_1-Q_0\right)\\ q^{\prime }\left(1\right)=\left(3\beta +4\right)\left(Q_7-Q_6\right)\end{array}$ 。

性质2 凸包性。

性质3 对称性。

性质4 几何不变性与仿射不变性。

3.3. 形状参数的几何意义

为阐明形状参数 $\beta$ 对 $\beta B$ 曲线形状的影响，类似于2.3节的分析，接下来讨论参数 $\beta$ 的几何意义。 $\beta B$ 基也可以由七次Bernstein基函数线性表出，即

$\{\begin{array}{l}{c}_{0,7}\left(t\right)=B_{0,7}\left(t\right)+\frac{3-3\beta }{7}{B}_{1,7}\left(t\right)+\frac{3-3\beta }{21}{B}_{2,7}\left(t\right)+\frac{1-\beta }{35}{B}_{3,7}\left(t\right)\\ c_{1,7}\left(t\right)=\frac{4+3\beta }{7}{B}_{1,7}\left(t\right)+\frac{8-8\beta }{21}{B}_{2,7}\left(t\right)+\frac{4-4\beta }{35}{B}_{3,7}\left(t\right)\\ c_{2,7}\left(t\right)=\frac{10+11\beta }{21}{B}_{2,7}\left(t\right)+\frac{10-10\beta }{35}{B}_{3,7}\left(t\right)\\ c_{3,7}\left(t\right)=\frac{20+15\beta }{35}{B}_{3,7}\left(t\right)\\ c_{4,7}\left(t\right)=\frac{20+15\beta }{35}{B}_{4,7}\left(t\right)\\ c_{5,7}\left(t\right)=\frac{10-10\beta }{35}{B}_{4,7}\left(t\right)+\frac{10+11\beta }{21}{B}_{5,7}\left(t\right)\\ c_{6,7}\left(t\right)=\frac{4-4\beta }{35}{B}_{4,7}\left(t\right)+\frac{8-8\beta }{21}{B}_{5,7}\left(t\right)+\frac{4+3\beta }{7}{B}_{6,7}\left(t\right)\\ c_{7,7}\left(t\right)=\frac{1-\beta }{35}{B}_{4,7}\left(t\right)+\frac{3-3\beta }{21}{B}_{5,7}\left(t\right)+\frac{3-3\beta }{7}{B}_{6,7}\left(t\right)+B_{7,7}\left(t\right)\end{array}$ (10)

记作

$c=NB$

其中，

$c={\left(\begin{array}{cccc}{c}_{0,7}\left(t\right)& c_{1,7}\left(t\right)& \cdots & c_{7,7}\left(t\right)\end{array}\right)}^{\text{T}}$ ，

$N=\left(\begin{array}{cccccccc}1& \frac{3-3\beta }{7}& \frac{3-3\beta }{21}& \frac{1-\beta }{35}& 0& 0& 0& 0\\ 0& \frac{4+3\beta }{7}& \frac{8-8\beta }{21}& \frac{4-4\beta }{35}& 0& 0& 0& 0\\ 0& 0& \frac{10+11\beta }{21}& \frac{10-10\beta }{35}& 0& 0& 0& 0\\ 0& 0& 0& \frac{20+15\beta }{35}& 0& 0& 0& 0\\ 0& 0& 0& 0& \frac{20+15\beta }{35}& 0& 0& 0\\ 0& 0& 0& 0& \frac{10-10\beta }{35}& \frac{10+11\beta }{21}& 0& 0\\ 0& 0& 0& 0& \frac{4-4\beta }{35}& \frac{8-8\beta }{21}& \frac{4+3\beta }{7}& 0\\ 0& 0& 0& 0& \frac{1-\beta }{35}& \frac{3-3\beta }{21}& \frac{3-3\beta }{7}& 1\end{array}\right)$ ，

$B={\left(\begin{array}{cccc}{B}_{0,7}\left(t\right)& B_{1,7}\left(t\right)& \cdots & B_{7,7}\left(t\right)\end{array}\right)}^{\text{T}}$ 。

如果令

$Q=\left(\begin{array}{cccc}{Q}_0& Q_1& \cdots & Q_7\end{array}\right)$

则式(9)可以等价表示为

$q\left(t\right)=QNB$ (11)

仍然将七次Bézier曲线的控制顶点记作 $V_i\left(i=0,1,\cdots ,7\right)$ ，并令

$V=\left(\begin{array}{cccc}{V}_0& V_1& \cdots & V_7\end{array}\right)$

故 $\beta B$ 曲线也可以转化为七次Bézier曲线表示形式，即

$q\left(t\right)=VB$ (12)

比较式(11)和式(12)可得

$V=QN$ (13)

即

$\{\begin{array}{ll}{V}_0=Q_0\hfill & \left(\text{a}\right)\hfill \\ V_1=\frac{3-3\beta }{7}{Q}_0+\frac{4+3\beta }{7}{Q}_1\hfill & \left(\text{b}\right)\hfill \\ V_2=\frac{3-3\beta }{21}{Q}_0+\frac{8-8\beta }{21}{Q}_1+\frac{10+11\beta }{21}{Q}_2\hfill & \left(\text{c}\right)\hfill \\ V_3=\frac{1-\beta }{35}{Q}_0+\frac{4-4\beta }{35}{Q}_1+\frac{10-10\beta }{35}{Q}_2+\frac{20+15\beta }{35}{Q}_3\hfill & \left(\text{d}\right)\hfill \\ V_4=\frac{20+15\beta }{35}{Q}_4+\frac{10-10\beta }{35}{Q}_5+\frac{4-4\beta }{35}{Q}_6+\frac{1-\beta }{35}{Q}_7\hfill & \left(\text{e}\right)\hfill \\ V_5=\frac{10+11\beta }{21}{Q}_5+\frac{8-8\beta }{21}{Q}_6+\frac{3-3\beta }{21}{Q}_7\hfill & \left(\text{f}\right)\hfill \\ V_6=\frac{4+3\beta }{7}{Q}_6+\frac{3-3\beta }{7}{Q}_7\hfill & \left(\text{g}\right)\hfill \\ V_7=Q_7\hfill & \left(\text{h}\right)\hfill \end{array}$ (14)

式(14c)可以等价表示为

$V_2=\frac{3-3\beta }{21}{Q}_0+\frac{8-8\beta }{21}{Q}_1+\frac{10+11\beta }{21}{Q}_2=Q_1+\frac{3-3\beta }{21}\left(Q_0-Q_1\right)+\frac{10+11\beta }{21}\left(Q_2-Q_1\right)$ (15)

同理，式(14f)可以等价表示为

$V_5=\frac{10+11\beta }{21}{Q}_5+\frac{8-8\beta }{21}{Q}_6+\frac{3-3\beta }{21}{Q}_7=Q_6+\frac{10+11\beta }{21}\left(Q_5-Q_6\right)+\frac{3-3\beta }{21}\left(Q_7-Q_6\right)$ (16)

形状参数 $\beta$ 的几何解释：由式(14b)可知， $Q_0{V}_1:V_1{Q}_1=4+3\beta :3-3\beta$ ；由式(14g)可知， $Q_3{V}_3:V_3{Q}_4=3-3\beta :4+3\beta$ ；由式(15)可知， $V_2$ 位于以 $\frac{3-3\beta }{21}\left(Q_0-Q_1\right)$ 和 $\frac{10+11\beta }{21}\left(Q_2-Q_1\right)$ 为邻边的平行四边形的终点处；由式(16)可知， $V_5$ 位于以 $\frac{10+11\beta }{21}\left(Q_5-Q_6\right)$ 和 $\frac{3-3\beta }{21}\left(Q_7-Q_6\right)$ 为邻边的平行四边形的终点处。令 $\beta =0$ ， $\beta B$ 曲线的控制多边形为 $Q_0{Q}_1\cdots Q_7$ ，而与 $\beta B$ 曲线等价的Bézier曲线的控制多边形为 $V_0{V}_1\cdots V_7$ ，如图4所示。

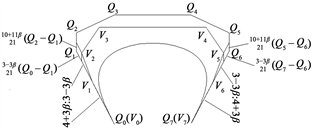
Figure 4. The geometric meaning of shape parameter $\beta$

图4. 形状参数 $\beta$ 的几何意义

3.4. 形状参数对曲线的影响

通过3.3节的分析可知，当 $\beta$ 不断增大时，与 $\beta B$ 曲线等价的七次Bézier曲线的控制多边形将会渐渐靠近 $\beta B$ 曲线的控制多边形。结合Bézier曲线的逼近性可知，当 $\beta$ 越大时， $\beta B$ 曲线也会越来越靠近其控制多边形。图5中依次取形状参数 $\beta =0,\frac{1}{3},\frac{2}{3},1$ 生成曲线1~4，其中，曲线1和4分别为由 $Q_0{Q}_1\cdots Q_7$ 所定义的七次Said-Ball曲线和Bézier曲线。

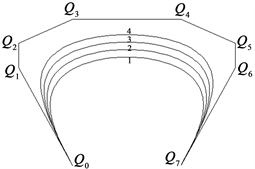
Figure 5. $\beta B$ curves with different values of $\beta$

图5. $\beta$ 不同取值时的 $\beta B$ 曲线

3.5. 曲线的几何作图法

由3.3节可知， $\beta B$ 曲线不仅可以转化为七次Bézier曲线，并且 $\beta B$ 曲线与七次Bézier曲线的控制顶点之间的显性关系可表示为式(14)。所以给定 $\beta B$ 曲线的控制顶点后，设计人员可以先根据式(14)求解其等价的七次Bézier曲线的控制顶点，然后采用Bézier曲线的几何作图法，由七级递推后得到的最后一个点即为 $\beta B$ 曲线上的点。当 $\beta =0$ ， $t=\frac{1}{2}$ 时，如图6所示， $Q_0{Q}_1\cdots Q_7$ 为 $\beta B$ 曲线的控制多边形， $V_0{V}_1\cdots V_7$ 为该 $\beta B$ 曲线等价的七次Bézier曲线的控制多边形。

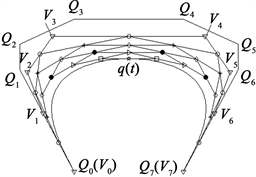
Figure 6. The geometric drawing method of $\beta B$ curves

图6. $\beta B$ 曲线的几何作图法

4. 结束语

本文给出了两种新的七次广义Ball曲线，即 $\alpha B$ 曲线与 $\beta B$ 曲线。 $\alpha B$ 曲线与 $\beta B$ 曲线均具有形状可调性： $\alpha B$ 曲线通过改变形状参数 $\alpha$ 的取值不仅可以转化为七次Wang-Ball和Said-Ball曲线，还可以得到无数条处于两者之间的曲线；而 $\beta B$ 曲线通过改变形状参数 $\beta$ 的取值不仅可以转化为七次Said-Ball和Bézier曲线，而且可以得到无数条介于两者之间的曲线。对比文献 [7] [8] ，因为本文构造的两种新的基函数的表达式均为显性，所以整体更加简洁明了。此外，形状参数 $\alpha$ 和 $\beta$ 具有明确的几何意义，便于设计员通过调整形状参数的值构造所需的曲线。

基金项目

国家自然科学基金(11761008)；江西省自然科学基金(20161BAB211028)；江西省教育厅科技项目(GJJ160558)。

NOTES

^*通讯作者。