碳化硅陶瓷超声振动运动轨迹以及磨削力建模

Modeling of Ultrasonic Vibration Trajectory and Grinding Force of Silicon Carbide Ceramics

摘要: 为了研究在磨削过程中超声振动对于加工的影响，现对单颗磨粒运动轨迹进行了数学理论模型以及仿真，并且在单颗粒运动学仿真的基础上，建立了超声振动磨削碳化硅的力学模型，结果表明：随着超声振动的加入，单位时间内磨粒运动轨迹长度也随之增加；在所选工艺参数范围内，高砂轮转速以及高超声振动频率能有效降低磨削力，小进给速度和小磨削切深度也能有效降低磨削力，加入了超声振动之后，磨削力下降幅度最高达到21.1%。

Abstract: In order to study the influence of ultrasonic vibration on machining during the grinding process, a mathematical theoretical model and simulation were conducted on the motion trajectory of a single abrasive particle. Based on the kinematic simulation of a single particle, a mechanical model for ul-trasonic vibration grinding of silicon carbide was established. The results showed that with the ad-dition of ultrasonic vibration, the length of the motion trajectory of the abrasive particle per unit time also increased; Within the selected process parameter range, high grinding wheel speed and high ultrasonic vibration frequency can effectively reduce grinding force. Small feed rate and cut-ting depth can also effectively reduce grinding force. After adding ultrasonic vibration, the maxi-mum reduction in grinding force can reach 21.1%.

1. 引言

与传统的高温合金材料相比，碳化硅陶瓷由于其耐高温性和耐腐蚀性等优良物理性能，被认为是航空航天工业中很有前途和有竞争力的材料。然而，碳化硅陶瓷也因其坚硬、脆性和各向异性的特点，是典型的难加工材料。为实现在碳化硅磨削过程中材料低损伤高效率的去除，许多学者进行了实验探索和建模不同过程的陶瓷基复合材料，发现其力学规律，为改善表面质量和减少工具磨损做出了巨大贡献。

Ding等 [1] 比较了碳化硅复合材料中有超声振动的制孔和无超声振动的制孔之间的差异，结果表明，超声振动使力和扭矩分别降低了23%和47.6%。Wang等 [2] 分析了碳化硅超声振动钻孔过程中超声振动与研磨力的关系。结果表明，通过调整超声波振动频率，可以降低刀具磨损和磨削力，提高表面加工质量。Diaz等 [3] 观察了SiCf/SiC复合材料的加工表面，并分析了残余应力的形成原理。结果表明，纤维区域存在残余拉伸应力，基体区域存在残余压缩应力。Dong等 [4] 在碳纤维增强碳化硅陶瓷制孔实验中加入了超声振动，结果发现随着超声振动的加入，制孔效率以及表面质量得到了进一步的提高，并且发现超声振动会导致单晶粒与材料之间的力学特性发生变化。Feng等 [5] 揭示了工艺参数对碳化物超声研磨过程中研磨力的影响。结果表明，超声波振动可以降低磨削力，而磨削力主要受进料速率的影响。Wang等 [6] 提出了一种新的倾斜螺旋孔铣削方法，应用于碳纤维增强塑料制孔，并将该方法与传统的螺旋孔铣削方法在理论上进行了比较。结果表明，该方法有利于去除切屑和降低切削力。他们还发现，该方法可以改善孔壁面光洁度，抑制缺陷，包括入口分裂和出口分层。Geng等人 [7] 将超声振动磨削技术应用于CFRP，结果表明，与传统的制孔方法相比，轴向力和侧向力显著降低，并改善了分层和表面粗糙度。Zhang等人 [8] 通过理论建立了材料在不同失效模式的临界失效载荷，并结合有限元分析，分析了芯支柱的长度和芯角以及面板厚度等几何参数对失效模式的影响，结果表面C/SIC材料内部晶粒堆叠对材料损伤有显著影响。Zhou等人 [9] 通过测量磨粒的突出高度和晶粒密度等表面特性，建立整个磨削区域的磨削力模型，验证了磨粒运动轨迹对磨削加工质量的影响。

本文建立了超声振动磨削碳化硅中单晶粒运动轨迹，并在MATLAB中对运动轨迹进行仿真，并且建立了材料去除的力学模型，分析不同磨削工艺参数对力的影响。

2. 运动轨迹建模

碳化硅超声振动磨削如图1所示。这个过程包括四种运动模式：砂轮绕孔轴的旋转运动，砂轮绕孔轴的旋转运动，磨轮轴向进给运动、超声波振动运动。多重运动的叠加使单晶粒的运动轨迹变得复杂。当工艺参数发生变化时，单个晶粒与工件之间的相对运动和相互作用也会发生变化。因此，通过对单晶粒运动轨迹的建模、模拟和分析，可以阐明加工过程中单晶粒与工件之间的相互力关系。并为研磨力模型的建立和工艺参数的选择提供了理论支持。在超声振动磨削过程中，磨轮底部的颗粒首先将工件与轴向进料接触，形成工件上部的机加工孔的轮廓。当砂轮继续进料时，材料被底部颗粒去除，侧面颗粒继续在孔壁上进行二次加工，以实现表面修整。由于材料的去除行为主要由磨轮侧面的晶粒完成，而研磨力也主要是由它们引起的，并且砂轮做螺旋运动，磨屑及时排出到磨粒与工件分离的区域。因此，本文在建模研磨力时，只考虑了侧面晶粒的去除行为，忽略底面上的晶粒，此外，在磨削过程中加入了大量磨削液，因此忽略磨削温度的影响，只对单个晶粒运动轨迹进行分析。

2.1. 运动学方程

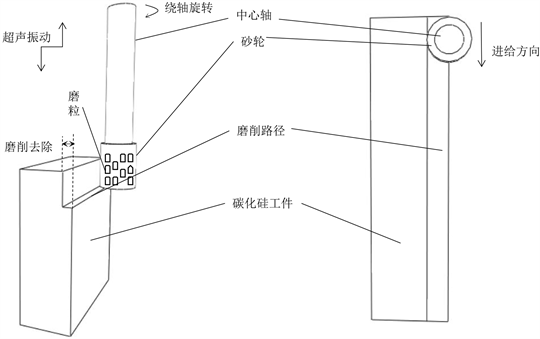
Figure 1. Ultrasonic vibration grinding process diagram (overview on the left and top view on the right)

图1. 超声振动磨削工艺图(左为总览图，右为俯视图)

2.1.1. 砂轮绕轴转动

在加工过程中，磨轮可以近似等同于一个圆柱体(如图1)，此时侧面磨粒以一定转速即角速度w绕着半径为a的磨轮进行圆周运动。当磨轮沿着碳化硅薄片向下做进给运动时，又会给磨粒提供沿着中心轴的线速度v，那么可以将磨粒的运动轨迹看作螺旋线。随着时间t的改变，磨粒运动轨迹方程如下：

$L\left(1\right)=\{\begin{array}{c}x=a\cos \left({\omega }_{1}t+{\phi }_1\right)=a\cos \left(\frac{2\pi n_1}{60}t+{\phi }_1\right)\\ y=a\sin \left({\omega }_{1}t+{\phi }_1\right)=a\sin \left(\frac{2\pi n_1}{60}t+{\phi }_1\right)\end{array}$ (1)

2.1.2. 砂轮进给运动

当未加入超声振动时，侧面单颗磨粒的运动轨迹为沿着水平或竖直轴线的直线运动，运动方程为：

$L\left(2\right)=vt$ (2)

2.1.3. 超声振动运动

当加入超声振动后，侧面磨粒的运动轨迹则改变为沿着轴线和振动波做往复运动，其中超声振动的振幅为A，频率为F，运动轨迹方程如下：

$L\left(3\right)=A\sin \left(2\pi Ft+{\phi }_2\right)$ (3)

将(1)~(3)方程组合起来，便得到了单颗磨粒在超声振动状态下的运动轨迹方程，如下：

$L\left(4\right)=\{\begin{array}{c}a\cos \left(\frac{2\pi n_1}{60}t+{\phi }_1\right)\\ a\sin \left(\frac{2\pi n_1}{60}t+{\phi }_1\right)+A\sin \left(2\pi Ft+{\phi }_2\right)\\ vt+A\sin \left(2\pi Ft+{\phi }_2\right)\end{array}$ (4)

2.2. 工艺参数对磨粒运动的影响

不同的工艺参数也会使得单颗磨粒的运动轨迹发生变化，进而影响加工件和被加工件之间的接触时间和作用程度。因此，分析单颗磨粒的运动轨迹不仅对探究磨削过程中有关材料去除率的问题有帮助，也为之后建立磨削力数学模型打下了基础。接着由于侧面磨粒除分布位置有所不同，它们的运动轨迹都大致相同，所以本文中用MATLAB对侧面单颗磨粒进行运动轨迹仿真，其他位置的颗粒不在仿真模拟。

下面是在MATLAB中改变加工工艺参数(进给速度、振幅等等)，得到的磨粒运动轨迹的变化图：

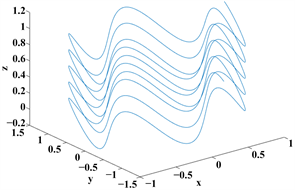
(a) (b)(c) (d)

Figure 2. Single abrasive particle motion trajectory diagram

图2. 单颗磨粒运动轨迹图

首先是单颗磨粒在空间中的运动状态，图2(a)图为未加入超声振动时，单颗磨粒的运动轨迹图，图2(b)和图2(c)图分别为在z轴方向和y轴方向加入超声振动，图2(d) 图为实际加入超声之后磨粒的运动轨迹(设加工时间为10秒，超声波振动的振幅为0.2 μm，频率为5 Hz，初始相位为 $\pi /4$ )。

由仿真可得，未加入超声振动时，磨粒所走过的轨迹曲线长度约为10.2250米，如图2(a)所示。加入超声振动后，此时将磨粒运动轨迹先分为z轴振动和y轴振动(与x轴同理)，将超声振动加在z轴上时，此时轨迹长度为12.1585米，如图2(b)所示；将超声振动y轴上时，轨迹曲线长度为11.1790米，如图2(c)所示；将z轴和y轴运动轨迹合成为一条之后，此时运动轨迹长度为13.3538米，如图2(d)所示。在单位加工时间内，轨迹曲线长度越长，说明此段时间内，磨粒在工件表面作用时间越长。即说明随着超声振动的加入，可以提高磨粒的加工效率。

紧接着继续改变加工工艺，将振幅从0.2 μm改为0.4 μm，其余加工条件不变，观察单颗磨粒运动轨迹的变化：

(a) (b) (c) (d) (e) (f)(g) (h)

Figure 3. Ultrasonic vibration abrasive particle motion trajectory under different process parameters

图3. 不同工艺参数下的超声振动磨粒运动轨迹图

从图3仿真结果可以得出，将振幅从0.2 μm改为0.4 μm之后，在加工时间还是为10秒，频率和初始相位保持不变的前提下，此时y轴上的磨粒运动轨迹长度为15.4986米(图3(c)和图3(d))，z轴上的磨粒运动轨迹长度为16.7648米(图3(e)和图3(f))，将两种运动合成之后，总运动轨迹长度变为20.6718米(图3(g)和图3(h))与之前相比磨粒运动轨迹长度增加了54.81%。这说明在一定范围内改变加工工艺参数之后，即使加工时间不变，依然可以起到优化加工的效果。

3. 超声振动辅助磨削力建模

3.1. 未变形磨屑平均厚度

在进行磨削分析时﹐为了计算方便，通常将磨粒进行简化。有些学者将磨粒简化为棱形，或者球形，而比较常见的是将磨粒简化为圆锥形。由于磨粒的尺寸非常小，这些简化模型的计算结果差异并不大。

本文将磨粒的形状简化为具有一定顶角的圆锥，圆锥的顶角为2θ，并假设磨粒在砂轮表面磨粒均匀分布，且不同磨粒突出高度相同。根据Hecker等人的研究论文证明 [10] ，未变形磨屑厚度是服从瑞利分布的。这样在忽略磨粒切削时产生的侧向隆起和工件和砂轮的变形的影响下，在磨削过程中磨粒的平均未变形磨屑厚度为：

$a_g^2=\sqrt{\frac{\pi }{4c}\frac{a_p{v}_w}{v_s{l}_a}\frac{1}{\tan \theta }}$ (5)

式中：C为单位面积上的有效磨粒数。

3.2. 切向磨削力和法向磨削力

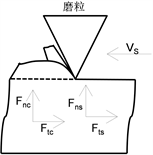
Figure 4. Decomposition diagram of single abrasive grinding force

图4. 单颗磨粒磨削力分解图

由磨削原理可知，法向磨削力 $F_n$ 及切向磨削力 $F_t$ 均由两部分组成，如图4所示。

$\{\begin{array}{l}{F}_n=F_{nc}+F_{ns}\hfill \\ F_t=F_{tc}+F_{ts}\hfill \end{array}$ (6)

其中， $F_{nc}$ –由于切削变形引起的法向力， $F_{ns}$ –由于摩擦引起的法向力， $F_{tc}$ –由于切削变形引起的切向力， $F_{ts}$ –由于摩擦引起的切向力。

由磨削定理中的试验可知，再以磨耗为主要磨损的磨削过程中，未发生烧伤前，磨粒顶部磨损面积率a与磨削力间呈线性关系。在不变磨削用量的前提下，由于法向磨削力随砂轮磨粒顶部磨损面积率增大而线性增大，所以，磨损平面与工件间的接触压强 $\bar{p}$ 为常数；另外，由于切向磨削力也随磨粒顶部磨损面积率增大而线性增大，所以，工件与磨损平面间的摩擦系数 $\mu$ 也是常数。

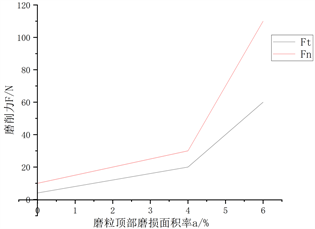
Figure 5. Schematic diagram of the relationship between wear area rate and grinding force

图5. 磨损面积率与磨削力关系示意图

图5是磨损面积率与磨削力关系示意图，若以 $a_r$ 代表工件与砂轮之间的实际接触面积，以 $A_f=l_{s}b$ 代表砂轮与工件的理论磨削接触面积，那么实际磨损平面与工件间的平均接触压强 $\bar{p}$ 应等于 $\text{d}{F}_n/\text{d}{a}_r$ ，也等于斜率 $\text{d}{F}_n/\text{d}a$ 与磨削接触面积 $A_f$ 之比，即：

$\bar{p}=\frac{\text{d}{F}_n}{\text{d}{a}_r}=\frac{\text{d}{F}_n}{\text{d}a}/l_s$ (7)

摩擦系数 $\mu$ 等于图中 $F_n$ 与 $F_t$ 曲线的斜率比，即：

$\mu =\frac{F_{ts}}{F_{ns}}=\frac{\text{d}{F}_t}{\text{d}a}/\frac{\text{d}{F}_n}{\text{d}a}$ (8)

对于单颗磨粒而言，由于摩擦而引起的法向磨削力为：

$F_{gns}=\bar{\delta }\bar{p}$ (9)

式中， $\bar{\delta }$ 为单颗磨粒的平均磨钝顶面积，即工件与工作磨粒的实际接触面积。

对于单颗磨粒而言，由于摩擦而引起的切向磨削力为：

$F_{gts}=\mu \bar{\delta }\bar{p}$ (10)

在纯剪切变形条件下，由于切屑变形而引起的单颗磨粒法向磨削力为：

$F_{gnc}=KA$ (11)

式中，K为单位磨削面积的磨削力，A为磨削截面积。

在纯剪切变形条件下，由于切屑变形而引起的单颗磨粒切向磨削力为：

$F_{gtc}=\phi KA$ (12)

其中， $\phi =\pi /\tan \theta$

式中，θ为磨粒顶圆锥半角，若取平均值θ = 52^。_，则φ = 0.61。

所以单颗磨粒的法向磨削力 $F_{gn}$ 和切向磨削力 $F_{gt}$ 的计算式分别为：

$\{\begin{array}{l}{F}_{gn}=F_{gnc}+F_{gns}=KA+\bar{\delta }\bar{p}\hfill \\ F_{gt}=F_{gtc}+F_{gts}=\phi KA+\mu \bar{\delta }\bar{p}\hfill \end{array}$ (13)

作用在砂轮与工件间的单位磨削宽度法向磨削力 ${F^{\prime }}_n$ 等于工件与砂轮接触面积中的单位磨削宽度上所有工作磨粒的法向力之和，即：

${F^{\prime }}_n={F^{\prime }}_{nc}+{F^{\prime }}_{ns}=K{{\displaystyle \sum }}^{\text{}}A{l}_s+N\bar{\delta }\bar{p}$ (14)

式中， ${{\displaystyle \sum }}^{\text{}}A{l}_s$ 为单位磨削宽度所有同时工作的各磨粒的切削截面积总和，即：

${{\displaystyle \sum }}^{\text{}}A{l}_s=\frac{V_w}{V_s}{a}_p$ (15)

N为单位磨削宽度上所有同时的磨粒数，即：

$N={\displaystyle {\int }_0^{l_s}Nd\left({l^{\prime }}_s\right)d\left({l^{\prime }}_s\right)}=\frac{A_g}{1+\alpha }{\left[c_1\right]}^{\beta }{\left[\frac{V_w}{V_s}\right]}^{\alpha }{\left[a_p\right]}^{\frac{1+\alpha }{2}}{\left[d_e\right]}^{\frac{1-\alpha }{2}}$ (16)

代入前式，则得到单位磨削宽度法向磨削力为：

$F_n=K\frac{V_w}{V_s}{a}_p+\frac{A_g\bar{\delta }\bar{p}}{1+\alpha }{\left[c_1\right]}^{\beta }{\left[\frac{V_w}{V_s}\right]}^{\alpha }{\left[a_p\right]}^{\frac{1+\alpha }{2}}{\left[d_e\right]}^{\frac{1-\alpha }{2}}$ (17)

同理，单位磨削宽度切向磨削力 ${F^{\prime }}_t$ 等于工件与砂轮接触面积中的单位磨削宽度上所有工作磨粒的切向力之和，即：

${F^{\prime }}_t={F^{\prime }}_{tc}+{F^{\prime }}_{ts}=\mu K{{\displaystyle \sum }}^{\text{}}A{l}_s+N\mu \bar{\delta }\bar{p}$ (18)

代入可得单位磨削宽度的切向磨削力：

${F^{\prime }}_t=\phi K\frac{V_w}{V_s}{a}_p+\frac{A_g\mu \bar{\delta }\bar{p}}{1+\alpha }{\left[c_1\right]}^{\beta }{\left[\frac{V_w}{V_s}\right]}^{\alpha }{\left[a_p\right]}^{\frac{1+\alpha }{2}}{\left[d_e\right]}^{\frac{1-\alpha }{2}}$ (19)

其中， $\alpha$ ， $\beta$ 为表征磨刃在砂轮圆周上分布状态的指数， $\alpha$ 通常取自[0, 2/3]之间， $\beta$ 通常取自[1/2, 2/3]之间， $d_e$ 为砂轮直径， $c_1$ 为磨刃密度。

经研究表明，加入超声振动之后，磨轮与工件表面间的摩擦因数会有变化，即会让摩擦因数变小，使得磨削力中由于摩擦产生的那一部分磨削力减少，从而整体的磨削力也随之减小。并根据在平面内任意角度的切向振动对摩擦力减小的影响，得出了添加振动后的摩擦力与没添加振动摩擦力之比可以表示为：

$\lambda \left(\xi \right)=\frac{1}{2\pi }{\displaystyle {\int }_0^{2\pi }\frac{\xi +\cos \vartheta \cos \tau }{\sqrt{\xi +2\xi \cos \vartheta \cos \tau +{\left(\cos \tau \right)}^2}}\text{d}\tau }$ (20)

其中， $\vartheta$ 为振动方向与物体宏观速度方向之间的夹角； $\xi$ 为物体的宏观速度与振动速度的幅值之比。

在轴向超声振动中， $\vartheta =\frac{\pi }{2}$ ，则单颗磨粒在超声振动作用下的摩擦力与没添加超声振动下的摩擦力之比为：

$\lambda \left(\xi \right)=\frac{2\xi }{\pi \sqrt{1+{\xi }^2}}K\left(\frac{1}{1+{\xi }^2}\right)$ (21)

其中，K为常数，由实验条件确定。

将此方程代入前面方程可得到超声振动状态下，单位宽度切向磨削力为：

${F^{\prime }}_t=\lambda \left(\xi \right)*\left(\phi K\frac{V_w}{V_s}{a}_p+\frac{a_g\mu \bar{\delta }\bar{p}}{1+\alpha }{\left[c_1\right]}^{\beta }{\left[\frac{V_w}{V_s}\right]}^{\alpha }{\left[a_p\right]}^{\frac{1+\alpha }{2}}{\left[d_e\right]}^{\frac{1-\alpha }{2}}\right)$ (22)

并且由于超声振动的添加，使得磨削力呈现周期性的变化，因此一个周期内的单位宽度法向平均磨削力可以表示为：

${\overline{F^{\prime }}}_t=\frac{1}{T}{\displaystyle {\int }_0^T{F^{\prime }}_t\text{d}T}=\frac{1}{T}{\displaystyle {\int }_0^T\lambda \left(\xi \right)*\left(\phi K\frac{V_w}{V_s}{a}_p+\frac{a_g\mu \bar{\delta }\bar{p}}{1+\alpha }{\left[c_1\right]}^{\beta }{\left[\frac{V_w}{V_s}\right]}^{\alpha }{\left[a_p\right]}^{\frac{1+\alpha }{2}}{\left[d_e\right]}^{\frac{1-\alpha }{2}}\right)\text{d}T}$ (23)

同理，一个周期内的单位宽度切向平均磨削力可以表示为：

${\overline{F^{\prime }}}_n=\frac{1}{T}{\displaystyle {\int }_0^T{F^{\prime }}_n\text{d}T}=\frac{1}{T}{\displaystyle {\int }_0^{T}K\frac{V_w}{V_s}{a}_p}+\frac{a_g\bar{\delta }\bar{p}}{1+\alpha }{\left[c_1\right]}^{\beta }{\left[\frac{V_w}{V_s}\right]}^{\alpha }{\left[a_p\right]}^{\frac{1+\alpha }{2}}{\left[d_e\right]}^{\frac{1-\alpha }{2}}\text{d}T$ (24)

4. 结果与分析

选定超声振动磨削过程中常用磨削工艺参数以及超声频率，代入方程中，可得到以下结果：由图6可以得出，可以看出，随着磨削力随着砂轮进给速度以及切深的提高而提高，随着砂轮转速以及超声频率的提高而降低，并且可以发现，即使在不同磨削工艺参数下，随着超声振动的加入，磨削力都随之降低。

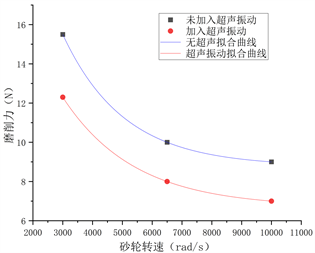
Figure 6. Diagram of the relationship between processing parameters and grinding force

图6. 加工工艺参数与磨削力关系图

5. 结论

1) 建立了砂轮磨粒在磨削过程中加入了超声振动后的运动轨迹方程。基于单颗磨粒运动仿真的结果，分析了不同工艺参数下单颗粒与工件的接触特性。仿真结果表面：随着超声振动的加入，在单位时间内，磨粒运动轨迹线的长度由10.225米增加到了13.3538米，增加幅度为30.6%，并且将振幅由0.2 μm提高0.4 μm之后，磨粒运动轨迹线长度进一步增加，增加到了20.6718米，增加幅度提高到了54.81%，这使得磨粒在材料表面作用时间增加，从而可以实验更好的加工效果。

2) 在明确了单颗磨粒与材料接触特性的基础上，建立力学模型，综合考虑材料去除过程中不同组分的力学组成。仿真结果表面：未加入磨削力模型计算的磨削力和与加入磨削振动后的磨削力模型计算出的磨削力变化趋势相同，随磨削深度、进给速度的增大而增大，随着砂轮转速以及超声频率的增大而减小，这验证了模型的准确性；并且在实验参数范围内，当加入超声振动之后，磨削力最大下降幅度为21.1%。