竞争风险下Fine-Gray模型与Cox模型的比较与评价

Comparison and Evaluation of Fine-Gray and Cox Models under Competitive Risks

摘要: 在生存分析中经常会遇到存在竞争风险的情形，在存在竞争风险情形下，比较Cox模型与Fine-Gray模型估计的分析效果。本文介绍了在存在竞争风险情形下的Fine-Gray模型，举例说明了Fine-Gray模型风险集的定义以及权重计算方法，并利用Cox模型与Fine-Gray模型对实际存在竞争风险的数据集进行了实例分析，结果表明，Fine-Gray模型与Cox模型分析结果不同，尤其是Cox模型会高估事件的累计发生率。因此，在生存分析中存在竞争风险时，选择Fine-Gray模型进行建模是更适合的。

Abstract: In survival analysis, scenarios with competing risks are frequently encountered. In the presence of competing risks, the analysis performance of the Cox model and the Fine-Gray model is compared. This paper introduces the Fine-Gray model in the context of competing risks, providing a detailed explanation of the definition of the Fine-Gray model’s risk set and the calculation method for weights. Through example analysis using actual data with competing risks, the paper demonstrates that the results of the Fine-Gray model and the Cox model differ, especially with the Cox model overestimating the cumulative incidence of events. Therefore, in survival analysis, when facing competing risks, choosing the Fine-Gray model for modeling is more suitable.

1. 引言

在许多学科领域，如医学、生物学、保险精算学、经济学以及人口统计学等多个领域都需要研究生存分析问题，当所研究的问题只存在单一结局时，Kaplan和Meier提出的K-M方法 [1] 和Cox提出的Cox模型 [2] 是最为常用的方法，Cox模型是一种常用的生存分析模型，用于探讨与生存时间相关的因素。它假设风险比在时间的推移过程中是恒定的，不随时间变化。在被给出的协变量集合 $x_{1i},x_{2i},\cdots ,x_{mi}$ 下，个体i的风险可以分解成两个部分，一部分是包括协变量不包括时间，一部分包括时间不包括协变量。Cox模型基本形式如下：

$h_i\left(t\right)=h_0\left(t\right)\exp \left\{{\beta }_1{x}_{1j}+\cdots +{\beta }_m{x}_{mj}\right\}$

其中 $h_0\left(t\right)$ 是基线危险函数， ${\beta }_1,{\beta }_2,\cdots ,{\beta }_m$ 是需要估计的参数或系数。 $t_1<t_2<\cdots <t_r$ 是惟一的有序感兴趣时间点，回归系数 ${\beta }_1,{\beta }_2,\cdots ,{\beta }_m$ 由偏似然方程的最大值决定。累积危险函数为 $H\left(t\right)={\displaystyle {\int }_0^{t}h\left(u\right)\text{d}u}$ ，累积分布函数 $F\left(t\right)$ 可由 $H\left(t\right)$ 导出， $F\left(t\right)=1-\exp \left(-H\left(t\right)\right)$ 。

然而，所研究的问题并不总是单一结局的，因此在某些情况下，上述方法可能并不适用，其中一种情况就是存在竞争风险，Gelman [3] 和Gooley [4] 对竞争风险理论进行了描述，Kalbfleisch和Prentice [5] 提出了一种考虑竞争风险的方法，在存在竞争风险条件下，事件i发生在时间t之前的概率分布叫做子分布，类型i事件的累计发生率函数被定义为 $F_i\left(t\right)=P\left(T\le t,C=i\right)$ ，记为CIF，Fine和Gray [6] 于1999年提出了Fine-Gray模型，这是一种基于CIF建模的一种竞争风险模型，然而，所研究的问题并不总是单一结局的，因此在某些情况下，上述方法可能并不适用，其中一种情况就是存在竞争风险，Gelman [3] 和Gooley [4] 对竞争风险理论进行了描述，Kalbfleisch和Prentice [5] 提出了一种考虑竞争风险的方法，在存在竞争风险条件下，事件i发生在时间t之前的概率分布叫做子分布，类型i事件的累计发生率函数被定义为 $F_i\left(t\right)=P\left(T\le t,C=i\right)$ ，记为CIF，Fine和Gray [6] 于1999年提出了Fine-Gray模型，这是一种基于CIF建模的竞争风险模型，Fine-Gray模型在存在竞争风险的生存分析实际问题中有着广泛应用，朱旭 [7] 和钱迪 [8] 等分别以胃癌和肝癌患者为样本构建Fine-Gray模型研究生存分析问题。

2. Fine-Gray模型介绍

该模型基于

$\gamma \left(t,x\right)={\gamma }_0\left(t\right){\text{e}}^{\beta x}$

这里的 $\gamma$ 是子分布危险函数， ${\gamma }_0$ 是子分布的基线危险函数，x是协变量向量， $\beta$ 是回归系数。其中子分布危险函数为

${\gamma }_i\left(t\right)=\underset{\delta t\to 0}{\lim }\left\{\frac{P\left(t<T<t+\delta t,C=i|T>t或T\le t且C\ne i\right)}{\delta t}\right\}$

偏似然方程为

$L\left(\beta \right)={\displaystyle \underset{j=1}{\overset{r}{\prod }}\frac{\exp \left(\beta x_j\right)}{{\displaystyle {\sum }_{i\in R_j}{w}_{ji}\exp \left(\beta x_i\right)}}}$

在所有的感兴趣的事件被观察到的时间点取乘积，其中 $t_1<t_2<\cdots <t_r$ 。Fine-Gray模型的偏似然形式和Cox比例风险模型相似，与Cox比例风险模型相比，Fine-Gray模型主要有两个差异，风险集合 $R_j$ 定义方式不同以及引入了删失生存权重 $w_{ji}$ 。风险集合 $R_j$ 由在时间t之前未经历事件的个体和在时间t之前经历了一个竞争风险事件的个体组成。

$R_j\left(t\right)=\left\{i:T_i\ge t或T_i\le t并且经历过一个竞争风险事件的个体\right\}$

因此，那些经历过竞争风险事件的个体一直处于风险集中。在存在竞争风险的前提下，一种类型i事件在时间t之前不发生的概率称为子生存函数，定义为 $S_i\left(t\right)=P\left(T>t,C=i\right)$ 。

删失生存概率权重 $w_{ji}$ 定义为

$w_{ji}=\frac{\hat{S}\left(t_j\right)}{\hat{S}\left(\min \left(t_j,t_i\right)\right)}$

这里的 $\hat{S}$ 是删失生存分布函数的一个K-M估计，需要解释一下，删失生存分布定义为 $\left(T_i,C_i\right)$ ，这里的 $T_i$ 定义为观察到第一个事件的时间，如果未观察到事件则 $C_i=1$ ，而观察到事件时 $C_i=0$ 。在每个观测到感兴趣事件发生的时间点(下标为j)，风险集合由在时间t之前未经历事件的个体和在时间t之前经历了一个竞争风险事件的个体组成。对给出的部分似然的对数进行求导，得到得分统计量：

$U\left(\beta \right)={\displaystyle \underset{j=1}{\overset{r}{\sum }}\left\{x_j-\frac{{\displaystyle {\sum }_{i\in R_j}{w}_{ji}{x}_i\exp \left(x_i\beta \right)}}{{\displaystyle {\sum }_{i\in R_j}{w}_{ji}\exp \left(x_i\beta \right)}}\right\}}$

$\hat{\beta }$ 表示回归系数 $\beta$ 的估计，是函数 $U\left(\beta \right)=0$ 时 $\beta$ 的取值。

为说明Fine-Gray模型的计算过程，给出示例数据集见表1。表1中包括10个观测个体，其观测到的时间点，事件类型，每个个体协变量为分别在表1的第1~4列。

Table 1. Example dataset

表1. 示例数据集

备注：事件类型I：感兴趣事件；事件类型II：竞争风险事件 ；事件类型III：删失。

表1第5列给出了删失分布生存函数估计值 $\hat{S}$ ，这里的 $\hat{S}$ 由K-M估计计算可得，K-M方法的过程如下：假定 $t_1<t_2<\cdots <t_r$ 是唯一的删失时间点，设 $d_j$ 为在 $t_j$ 时间发生删失的个体数量， $n_j$ 为在 $t_j$ 之前有经历该事件风险的个体数量。则

$\hat{S}\left(t\right)={\displaystyle \underset{t_j\le t}{\prod }\frac{n_j-d_j}{n_j}}$

在10个观测个体中，有4个个体发生删失。删失时间点分别在 $t=t_1,t_2,t_6,t_9$ ，这4个删失时间点的生存分布 $\hat{S}$ 值，计算如下；

$\begin{array}{l}\hat{S}\left(t_1\right)=\frac{10-1}{10}=0.90\\ \hat{S}\left(t_2\right)=\hat{S}\left(t_1\right)\times \frac{8}{9}=0.80\\ \hat{S}\left(t_6\right)=\hat{S}\left(t_2\right)\times \frac{4}{5}=0.64\\ \hat{S}\left(t_9\right)=\hat{S}\left(t_6\right)\times \frac{1}{2}=0.32\end{array}$

在其他未发生删失6个时间点，每个时间点的生存函数估计值 $\hat{S}$ 与小于该时间点的前一个删失时间点的生存估计值相同。

在得到各个时间点的生存函数估计值后，可以计算删失生存概率权重 $w_{ji}$ ，计算过程见表2。观测个体单元在第1行，感兴趣(类型I)事件发生的时间点在第1列，表中数据为类型I事件在各阶段所在风险集中取得的权重 $w_{ji}$ 。

Table 2. Calculation process of weights w j i for deleted survival probabilities

表2. 删失生存概率权重 $w_{ji}$ 的计算过程

备注：表中“−”表示该单元对应时间点 $t_i$ 不在讨论的风险集 $R_j$ 中。

对于感兴趣事件(类型I)，竞争风险事件(类型II)，删失(类型III) 3种不同类型事件，10个观测个体他们在不同时刻的权重也不相同。

注意，在风险集 $R_j$ 中，对于时间点 $t_j$ ，当 $t_j\le t_i$ 时，由 $\min \left(t_j,t_i\right)=t_j$ ，此时

$w_{ji}=\frac{\hat{S}\left(t_j\right)}{\hat{S}\left(\min \left(t_j,t_i\right)\right)}=1$

当 $t_j>t_i$ 时，权重小于1。

以个体4为例，其对应的删失生存概率权重 $w_{ji}$ 为

$w_{4i}=\frac{\hat{S}\left(t_4\right)}{\hat{S}\left(\min \left(t_4,t_i\right)\right)}$

个体1和个体2在 $t=t_1$ 和 $t=t_2$ 时发生删失，在此之前没有观测到感兴趣事件，因此不在风险集中，个体3在 $t=t_3$ 时观测到感兴趣事件，它只参与了第一项的部分似然，权重为1，个体4在 $t=t_4$ 时观测到竞争风险事件，在 $t_4$ 之前，权重为1，随着时间推移，权重逐渐降低。个体5在 $t=t_5$ 时观测到感兴趣事件，参与了前两项的部分似然，权重为1。

对于本例，需要求解的得分统计量为：

$\begin{array}{c}U\left(\beta \right)=x_3-\frac{w_{33}{x}_3{\text{e}}^{x_3\beta }+w_{34}{x}_4{\text{e}}^{x_4\beta }+\cdots +w_{3,10}{x}_{10}{\text{e}}^{x_{10}\beta }}{w_{33}{\text{e}}^{x_2\beta }+w_{34}{\text{e}}^{x_4\beta }+\cdots +w_{3,10}{\text{e}}^{x_{10}\beta }}\\ +x_5-\frac{w_{54}{x}_4{\text{e}}^{x_4\beta }+w_{55}{x}_5{\text{e}}^{x_5\beta }+\cdots +w_{5,10}{x}_{10}{\text{e}}^{x_{10}\beta }}{w_{54}{\text{e}}^{x_4\beta }+w_{55}{\text{e}}^{x_5\beta }+\cdots +w_{5,10}{\text{e}}^{x_{10}\beta }}\\ +x_7-\frac{w_{74}{x}_4{\text{e}}^{x_4\beta }+w_{77}{x}_7{\text{e}}^{x_7\beta }+\cdots +w_{7,10}{x}_{10}{\text{e}}^{x_{10}\beta }}{w_{74}{\text{e}}^{x_4\beta }+w_{77}{\text{e}}^{x_7\beta }+\cdots +w_{7,10}{\text{e}}^{x_{10}\beta }}\\ +x_{10}-\frac{w_{10,4}{x}_4{\text{e}}^{x_4\beta }+w_{10,8}{x}_8{\text{e}}^{x_8\beta }+w_{10,10}{x}_{10}{\text{e}}^{x_{10}\beta }}{w_{10,4}{\text{e}}^{x_4\beta }+w_{10,8}{\text{e}}^{x_8\beta }+w_{10,10}{\text{e}}^{x_{10}\beta }}\\ =0\end{array}$

将表2中的权重值和表1中的x代入可得

$\begin{array}{c}U\left(\beta \right)=8-\frac{8e^{8\beta }+9e^{9\beta }+7e^{7\beta }+10e^{10\beta }+11e^{11\beta }+13e^{13\beta }+8e^{8\beta }+9e^{9\beta }}{e^{8\beta }+e^{9\beta }+e^{7\beta }+e^{10\beta }+e^{11\beta }+e^{13\beta }+e^{8\beta }+e^{9\beta }}\\ +7-\frac{9e^{9\beta }+7e^{7\beta }+10e^{10\beta }+11e^{11\beta }+13e^{13\beta }+8e^{8\beta }+9e^{9\beta }}{e^{9\beta }+e^{7\beta }+e^{10\beta }+e^{11\beta }+e^{13\beta }+e^{8\beta }+e^{9\beta }}\\ +11-\frac{0.8\times 9e^{9\beta }+11e^{11\beta }+13e^{13\beta }+8e^{8\beta }+9e^{9\beta }}{0.8e^{9\beta }+e^{11\beta }+e^{13\beta }+e^{8\beta }+e^{9\beta }}\\ +9-\frac{0.4\times 9e^{9\beta }+0.5\times 13e^{13\beta }+9e^{9\beta }}{0.4\times e^{9\beta }+0.5\times e^{13\beta }+e^{9\beta }}\\ =0\end{array}$

可以算出函数的解 $\hat{\beta }=-0.\text{4363}$ 。

3. 基于Fine-Gray模型的CIF估计

定义 $H\left(t\right)$ 为子分布的累计危险函数，它的估计计算方法如下

$\hat{H}\left(t;x_0,\hat{\beta }\right)={\displaystyle \underset{t_j\le t}{\sum }\left\{\frac{\exp \left(x_0\hat{\beta }\right)}{{\displaystyle {\sum }_{i\in R_j}{w}_{ji}\exp \left(x_i\hat{\beta }\right)}}\right\}}$

其中t表示感兴趣的时间点， $x_0$ 为代入的协变量， $\hat{\beta }$ 为回归系数的估计值。

通过累积危险函数 $H\left(t\right)$ 可计算CIF的估计值，计算公式如下：

$F\left(t\right)=1-\exp \left(-H(\; t\; )\right)$

利用表1中的示例数据集，代入4个感兴趣时间点及对应协变量，计算累计危险函数以及CIF的估计值。

$\begin{array}{c}\hat{H}\left(t=t_3;x_0=8,\hat{\beta }=-0.\text{4363}\right)=\frac{{\text{e}}^{8\hat{\beta }}}{{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ =\text{0}\text{.1773}\end{array}$

$\begin{array}{c}\hat{H}\left(t=t_5;x_0=7,\hat{\beta }=-0.4363\right)=\frac{{\text{e}}^{7\hat{\beta }}}{{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ +\frac{{\text{e}}^{7\hat{\beta }}}{{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ =0.2743\end{array}$

$\begin{array}{c}\hat{H}\left(t=t_7;x_0=11,\hat{\beta }=-0.4363\right)=\frac{{\text{e}}^{11\hat{\beta }}}{{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ +\frac{{\text{e}}^{11\hat{\beta }}}{{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ +\frac{{\text{e}}^{11\hat{\beta }}}{0.8{\text{e}}^{9\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ =0.0479\end{array}$

$\begin{array}{c}\hat{H}\left(t=t_{10};x_0=9,\hat{\beta }=-0.4363\right)=\frac{{\text{e}}^{9\hat{\beta }}}{{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ +\frac{{\text{e}}^{9\hat{\beta }}}{{\text{e}}^{9\hat{\beta }}+{\text{e}}^{7\hat{\beta }}+{\text{e}}^{10\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ +\frac{{\text{e}}^{9\hat{\beta }}}{0.8{\text{e}}^{9\hat{\beta }}+{\text{e}}^{11\hat{\beta }}+{\text{e}}^{13\hat{\beta }}+{\text{e}}^{8\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ +\frac{{\text{e}}^{9\hat{\beta }}}{0.4{\text{e}}^{9\hat{\beta }}+0.5{\text{e}}^{13\hat{\beta }}+{\text{e}}^{9\hat{\beta }}}\\ =0.6724\end{array}$

CIF的估计值为

$\begin{array}{l}\hat{F}\left(t=t_3;x_0=8,\hat{\beta }=-0.4363\right)=1-{\text{e}}^{-\hat{H}\left(t=t_3;x_0=8,\hat{\beta }=-0.4363\right)}=0.1625\\ \hat{F}\left(t=t_5;x_0=7,\hat{\beta }=-0.4363\right)=1-{\text{e}}^{-\hat{H}\left(t=t_5;x_0=7,\hat{\beta }=-0.4363\right)}=0.2399\\ \hat{F}\left(t=t_7;x_0=11,\hat{\beta }=-0.4363\right)=1-{\text{e}}^{-\hat{H}\left(t=t_7;x_0=11,\hat{\beta }=-0.4363\right)}=0.0468\\ \hat{F}\left(t=t_{10};x_0=9,\hat{\beta }=-0.4363\right)=1-{\text{e}}^{-\hat{H}\left(t=t_{10};x_0=11,\hat{\beta }=-0.4363\right)}=0.4895\end{array}$

4. 实例分析

数据来自R中的数据集(survival包中的mgus2)，共计1371例单克隆丙种球蛋白病患者，其中结局事件定义为“发生浆细胞恶性肿瘤”有114例，而结局事件是在“发生浆细胞恶性肿瘤”之前因其他原因死亡患者有855例，这些发生“其他死亡”的患者因无法观察到“发生浆细胞恶性肿瘤”的终点，就被称为与“发生浆细胞恶性肿瘤”存在竞争风险的事件，其他402例患者是在观测期间上述结局事件没有发生。研究指标变量定义与赋值见表3。

Table 3. Definitions and assignments of variables

表3. 各变量的定义与赋值

协变量x有两个，分别为血红蛋白水平和年龄，记为x₁，x₂，创立协变量矩阵。生存时间t对类型I事件表示直至发展为浆细胞恶性肿瘤或最后一次访视时间，对类型II事件表示直到死亡或最后一次接触的时间，对类型III事件表示最后一次接触时间。

数据集mgus2中的各个变量的统计描述见表4。

Table 4. Statistical description of variables

表4. 变量的统计性描述

利用Fine-Gray模型分析建模，这里的协变量为x₁，x₂，自变量为生存时间t，响应变量为回归系数 $\hat{\beta }$ 。

如果用Cox模型进行回归分析，由于不考虑竞争风险，因此在考虑类型I事件时，将类型I事件为感兴趣事件，类型II和类型III事件改为删失事件，在考虑类型II事件时，则将类型II事件作为感兴趣事件，类型I和类型III事件改为删失事件。

利用Fine-Gray模型和Cox模型建模所得结果见表5。

Table 5. Comparison between Fine-Gray model and Cox model

表5. Fine-Gray模型与Cox模型对比

根据表5，可得出以下结果：

在对类型I事件建模中，Fine-Gray模型与Cox模型估计结果差异很大。Fine-Gray模型协变量x₁的回归系数不显著，x₂的回归系数显著。Cox模型估计结果则与之相反。而在对于类型II事件建模中，Fine-Gray模型与Cox模型估计结果非常接近。协变量x₁和x₂对应的回归系数都非常显著。说明利用Fine-Gray模型与Cox模型的建模区别主要体现在对类型I事件的估计结果上。主要由于Cox模型只针对样本中发生类型I事件114例的个体建模，而Fine-Gray模型在考虑了发生类型I事件的114例个体基础上，还考虑发生类型II (竞争风险)事件的855例个体，在建模过程中，通过表2中的权重计算方法，算出竞争风险事件个体的权重，并且随着时间推移，竞争风险事件个体在风险集中的权重逐渐降低。

为了更直观的说明Fine-Gray模型与Cox模型的区别，分别绘制类型I事件的累计发生率的曲线图。以mgus2数据集协变量的中位数 $x_1=13.5$ ， $x_2=72$ ，编号为135的患者为例，分别用Fine-Gray模型和Cox模型对发生浆细胞恶性肿瘤这一感兴趣事件的累计发生率进行预测，结果见图1。

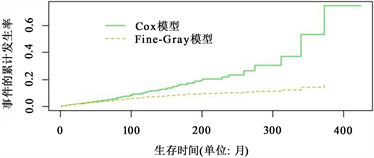
Figure 1. Predictive comparison between Fine-Gray model and Cox model

图1. Cox模型与Fine-Gray模型对比预测图

5. 结语

由第3部分实证对比分析可以看出，Fine-Gray模型适用于具有多个终点的生存数据，在存在竞争风险的情况下，得到的结果更符合实际，具有更好的拟合性。如临床上常见术后死亡患者无法获取关心终点，故术后死亡与关心终点存在竞争风险。相比之下，使用传统Cox模型会忽略竞争风险，可能高估所研究事件的累计发生率。

基金项目

本研究由2022年度辽宁省研究生教育教学改革研究项目(2022-180-39510165)资助。

NOTES

^*通讯作者。