带有抢占优先权和重试的排队系统的优化分析

Optimization Analysis of Queueing Systems with Preemptive Priority and Retrial

摘要: 本文研究了带有抢占优先权和重试的M/M/1排队系统。首先，采用概率生成函数的方法，得到了系统的稳态概率和主要性能指标。然后考虑了双目标优化的问题，旨在同时最小化系统成本和顾客逗留时间，借助NSGA-II算法来寻找Pareto最优解集。最后建立了以最优成本为因变量，非优先权顾客的到达率、最优逗留时间以及最优逗留时间的负指数为自变量建立了回归模型，进行了回归分析及模型的显著性检验。本文的分析能够使系统在提高服务质量的同时最小化成本，研究结论对系统管理者来说具有一定的参考价值。

Abstract: In this paper, the M/M/1 queueing system with preemption priority and retrial is studied. First, the steady state probability and main performance measures of the system are obtained by using probability generating function method. Then, the problem of Bi-objective optimization is consid-ered to minimize both system cost and customer’ sojourn time, and NSGA-II algorithm is used to find the optimal solution set of Pareto. Finally, a regression model is established with the optimal cost as the dependent variable, the arrival rate of non-priority customers, the optimal sojourn time and the negative index of the optimal sojourn time as independent variables, the regression analy-sis and the significance test of the model are carried out. The analysis of this paper can improve the service quality of the system while minimizing the cost, and the research conclusion has a certain reference value for system managers.

1. 引言

在优先权排队系统中，高优先权顾客相对于低优先权顾客有优先被服务的权利。White和Christie [1] 研究了抢占优先权排队系统，获得了稳态下系统中高优先权和低优先权顾客的平均队长。作为该模型的拓展，Avi-Itzhak和Naor [2] 考虑多顾客类型和一般服务时间的情况，他们假设被抢占的顾客再次获得服务时从被中断点重启服务，推导出多顾客类型一般服务时间的抢占优先权排队系统的性能指标。对于非抢占优先权排队的情况，Mores [3] 的著作中给出两类优先权顾客的M/M/1非抢占优先权排队系统的平均队长等性能指标。后来Wang等 [4] 研究了M/M/1非抢占优先级队列中的均衡策略，他们考虑了可观测和不可观测的情况，得出了顾客相应的均衡加入策略。而Li等 [5] 将不可观测的排队扩展到了更一般的多服务器情况，研究了具有同质顾客的M/M/n非抢占优先级排队的均衡策略。关于优先权排队的理论分析已经较为成熟，许多学者开始注重研究优先权排队的应用价值。Niyato等 [6] 把非抢占优先权的排队系统应用到无线网络中，讨论在不同休眠与工作策略下的系统性能。Wang等 [4] 提出用优先权排队系统来刻画认知无线电系统，探索改善服务质量的频谱管理方式。Do等 [7] 基于队长不可见的优先权排队模型，研究了认知无线电网络的社会最优策略。

重试排队系统是一个具有很强实际应用背景的排队模型。它在许多通信过程的性能分析中起着至关重要的作用。包括局域网和广域网、交换系统、共享总线局域网、数字窝蜂移动网络等。目前关于单服务台重试排队系统的理论分析已有大量的成果，Wang和Zhang研究了不同信息水平下单服务器重试队列中的均衡加入策略和社会最优加入策略 [8] 。张峰等研究了带有服务台休假和可修的重试排队系统，利用补充变量法和嵌入马尔科夫链求出了系统的稳态解，并进一步给出该系统的个体均衡策略和社会最优策略 [9] 。Jailaxmi对具有一般重试时间、M休假和冲突的M/G/1重试队列进行了性能分析 [10] 。而Lakaour等考虑了具有碰撞和传输错误的M/M/1重试队列 [11] 。Goel和Kulshrestha将重试策略的呼叫缓冲策略运用到认知无线电网络中，整个系统采用多维连续时间马尔可夫链建模，并据此导出系统的性能指标 [12] 。张钰和王金亭 [13] 研究了服务台不可靠的M/M/1常数率重试排队系统中顾客的均衡进队策略，并建立单位时间内服务商的收益和社会福利函数。比较发现，披露队长信息不一定能提高服务商收益和社会福利。

然而，大多数研究都关注单目标优化的问题，然后实际中需要同时考虑优化多个目标函数。Tavakkoli [14] 建立了双目标优化模型，同时解决了具有拥堵和定价策略的设施位置问题。Khodemani [15] 提出了双目标分层枢纽选址问题，同时最小化了总成本和总行程。本文考虑了一个基于抢占优先权和重试的M/M/1排队系统，并且考虑了双目标优化问题，旨在最小化系统成本和顾客的等待时间。最后建立了最小成本和最小逗留时间的回归模型，在诸多领域可以为系统管理者提供一些建议。

2. 模型描述

本模板考虑一个单服务器，两类顾客的M/M/1重试排队系统，其中PU为优先权顾客，SU为非优先权假设优先权顾客和非优先权顾客的到达间隔分别服从参数为 ${\lambda }_p$ 和 ${\lambda }_s$ 的指数分布。服务时间也服从指数分布，参数分别为 ${\mu }_p$ 和 ${\mu }_s$ 。当非优先权顾客到达系统时，如果服务台处于空间状态，它将立即获得服务。否则该用户将会进入一个无限空间重试轨道。当服务台空闲时，轨道中排在队首的顾客将会通过重试来获取服务。重试的时间间隔服从参数为 $\theta$ 的指数分布。假定两类顾客的到达间隔，服务时间，非优先权顾客的重试时间间隔都是相互独立的。在非优先权顾客的服务时间内，如果有优先权顾客到达，将会抢占非优先权顾客的服务。因此，服务台可以处于三种状态：空闲、为非优先权顾客服务、为优先权顾客服务。

系统的状态被描述为 $\left(C\left(t\right),X\left(t\right)\right)$ 的二维随机过程，其中 $X\left(t\right)$ 表示重试轨道中的次用户数量， $C\left(t\right)$ 表示服务台的状态， $C\left(t\right)$ 取值为0,1,2，分别表示服务台空闲，为优先权顾客服务，为非优先权顾客服务。

系统的状态和一步转移概率如图1所示。

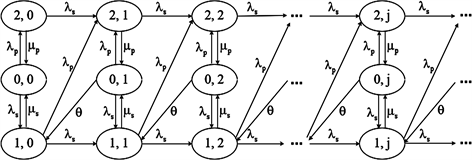
Figure 1. Histogram for the regression residuals

图1. 回归残差项直方图

3. 稳态分析

定理1 系统处在各个状态下的概率分别如下：

$P_0\left(1\right)=\frac{{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)}{{\mu }_s\left({\lambda }_p+{\mu }_p\right)},$

$P_1\left(1\right)=\frac{{\lambda }_s}{{\mu }_s},$

$P_2\left(1\right)=\frac{1}{{\lambda }_p+{\mu }_p}.$

证明 定义母函数为定义 $P\left(i,j\right)=\underset{t\to \infty }{\lim }P\left\{C\left(t\right)=i,N\left(t\right)=j\right\}$ 表示状态i下的平稳概率，定义生成函数 $P_i\left(z\right)={\displaystyle \underset{j=o}{\overset{\infty }{\sum }}{z}^j}P\left(i,j\right)$ ， $i=0,1,2$ ，其中， $\left|z\right|\le 1$ 。

系统的平衡方程如下：

$\left({\lambda }_p+{\lambda }_s\right)P\left(0,0\right)={\mu }_{p}P\left(2,0\right)+{\mu }_{s}P\left(1,0\right),$ (1)

$\left({\lambda }_p+{\lambda }_s+\theta \right)P\left(0,j\right)={\mu }_{p}P\left(2,j\right)+{\mu }_{s}P\left(1,j\right),j>1,$ (2)

$\left({\lambda }_p+{\lambda }_s+{\mu }_s\right)P\left(1,0\right)={\lambda }_{s}P\left(0,0\right)+\theta P\left(0,1\right),$ (3)

$\left({\lambda }_p+{\lambda }_s+{\mu }_s\right)P\left(1,j\right)={\lambda }_{s}P\left(0,j\right)+{\lambda }_{s}P\left(1,j-1\right)+\theta P\left(0,j+1\right),j>1,$ (4)

$\left({\lambda }_s+{\mu }_p\right)P\left(2,0\right)={\lambda }_{p}P\left(0,0\right),$ (5)

$\left({\lambda }_s+{\mu }_p\right)P\left(2,j\right)={\lambda }_{s}P\left(2,j-1\right)+{\lambda }_{p}P\left(0,j\right)+{\lambda }_{p}P\left(1,j-1\right),j>1,$ (6)

方程两边同时乘以 $z^j$ ，然后对它们求和，就得到：

$\left({\lambda }_p+{\lambda }_s+\theta \right)P_0\left(z\right)-\theta P\left(0,0\right)={\mu }_p{P}_2\left(z\right)+{\mu }_s{P}_1\left(z\right),$ (7)

$\left({\lambda }_p+{\lambda }_s+{\mu }_s\right)P_1\left(z\right)={\lambda }_s{P}_0\left(z\right)+{\lambda }_{s}z{P}_1\left(z\right)+\frac{\theta }{z}\left[P_0\left(z\right)-P\left(0,0\right)\right],$ (8)

$\left({\lambda }_s+{\mu }_p\right)P_2\left(z\right)={\lambda }_p{P}_0\left(z\right)+{\lambda }_{s}z{P}_2\left(z\right)+{\lambda }_{p}z{P}_1\left(z\right),$ (9)

结合(7)和(8)然后消去 $P\left(0,0\right)$ ，再结合(9)，并约去 $1-z$ ，我们得到：

${\lambda }_s\left[P_0\left(z\right)+P_1\left(z\right)+P_2\left(z\right)\right]={\mu }_s{P}_1\left(z\right).$ (10)

将 $z=1$ 代入式(7)，(9)和(10)，利用归一化条件，即可得到系统处在各状态下的平稳概率表达式。

4. 性能指标

定理2 系统处在各状态 $i,\left(i=1,2,3\right)$ 下的队列长度分别如下：

$P_0{}^{\prime }\left(1\right)=\frac{{\lambda }_s^2\left({\lambda }_p+{\mu }_s\right)\left[{\left({\lambda }_p+{\mu }_p\right)}^2\left({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)\right]}{{\mu }_s\left({\lambda }_s+\theta \right)\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left(({\lambda }_p+{\mu }_p\right)\right\}}+\frac{{\lambda }_s^2\left({\lambda }_p+{\mu }_p\right)+{\lambda }_s}{{\mu }_s\left({\lambda }_s+\theta \right)\left({\lambda }_p+{\mu }_p\right)},$

$P_1{}^{\prime }\left(1\right)=\frac{{\lambda }_s^2\left[{\left({\lambda }_p+{\mu }_p\right)}^2\left({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)\right]}{{\mu }_s\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left({\lambda }_p+{\mu }_p\right)\right\}},$

$\begin{array}{l}{P}_2{}^{\prime }\left(1\right)=\frac{{\lambda }_s^2{\lambda }_p\left({\lambda }_p+{\mu }_s\right)\left[{\left({\lambda }_p+{\mu }_p\right)}^2\left(({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)\right]}{{\mu }_p{\mu }_s\left({\lambda }_s+\theta \right)\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left({\lambda }_p+{\mu }_p\right)\right\}}\\ +\frac{\left({\lambda }_p+{\lambda }_s+\theta \right)\left[{\lambda }_s^2\left({\lambda }_p+{\mu }_p\right)+{\lambda }_s\right]}{{\mu }_p{\mu }_s\left({\lambda }_s+\theta \right)\left({\lambda }_p+{\mu }_p\right)}.\end{array}$

证明 对(7)，(9)，(10)分别求导得：

$\left({\lambda }_p+{\lambda }_s+\theta \right)P_0{}^{\prime }\left(z\right)={\mu }_p{P}_2{}^{\prime }\left(z\right)+{\mu }_s{P}_1{}^{\prime }\left(z\right),$ (11)

$\left({\lambda }_s+{\mu }_p\right)P_2{}^{\prime }\left(z\right)={\lambda }_p{P}_0{}^{\prime }\left(z\right)+{\lambda }_s{P}_2\left(z\right)+{\lambda }_{s}z{P}_2{}^{\prime }\left(z\right)+{\lambda }_p{P}_1\left(z\right)+{\lambda }_{p}z{P}_1{}^{\prime }\left(z\right),$ (12)

${\lambda }_s\left[P_0{}^{\prime }\left(z\right)+P_1{}^{\prime }\left(z\right)+P_2{}^{\prime }\left(z\right)\right]={\mu }_s{P}_1{}^{\prime }\left(z\right)-{\lambda }_s{P}_1\left(z\right).$ (13)

将 $z=1$ 代入(11)~(13)，并进行一系列求解，即可得到 $P_0{}^{\prime }\left(1\right),P_1{}^{\prime }\left(1\right),P_2{}^{\prime }\left(1\right)$ 的表达式。

定理3 平均系统队长和平均轨道队长分别表示如下：

$N_s=\frac{{\lambda }_s\left[{\left({\lambda }_p+{\mu }_p\right)}^2\left({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)\right]}{\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left({\lambda }_p+{\mu }_p\right)\right\}},$

$N_o=\frac{{\lambda }_s\left[{\left({\lambda }_p+{\mu }_p\right)}^2\left({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)\right]}{\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left({\lambda }_p+{\mu }_p\right)\right\}}-\frac{{\lambda }_s}{{\mu }_s}.$

证明 服务台处于状态i时，轨道中次用户的平均数量：

$E\left[R\right]={\displaystyle \underset{j=0}{\overset{\infty }{\sum }}jP\left(i,j\right),i=0,1,2,}$ (14)

因此，轨道中次用户的平均数量为：

$E\left[N\right]={\displaystyle \underset{i=0}{\overset{3}{\sum }}{\displaystyle \underset{j=1}{\overset{\infty }{\sum }}jP\left(i,j\right)}}=P_0{}^{\prime }\left(1\right)+P_1{}^{\prime }\left(1\right)+P_2{}^{\prime }\left(1\right),$ (15)

系统中次用户的平均数量：

$E\left[N_s\right]={\displaystyle \underset{i=0}{\overset{4}{\sum }}{\displaystyle \underset{j=1}{\overset{\infty }{\sum }}jP\left(i,j\right)}}+P\left(1\right)=P_0{}^{\prime }\left(1\right)+P_1{}^{\prime }\left(1\right)+P_2{}^{\prime }\left(1\right)+P_1\left(1\right).$ (16)

将定理3得到的结果代入(15)，(16)，即可得到队长的表达式。

定理4 平均逗留时间和平均等待时间分别表示如下：

$T_s\left(q\right)=\frac{{\left({\lambda }_p+{\mu }_p\right)}^2\left({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)}{\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left({\lambda }_p+{\mu }_p\right)\right\}},$

$T\left(q\right)=\frac{{\left({\lambda }_p+{\mu }_p\right)}^2\left({\lambda }_p+{\lambda }_s+\theta \right)+{\mu }_s\left({\lambda }_p+{\mu }_p+{\lambda }_s+\theta \right)}{\left({\lambda }_p+{\mu }_p\right)\left\{\left({\lambda }_s+\theta \right)\left[{\mu }_p{\mu }_s-{\lambda }_s\left({\lambda }_p+{\mu }_p\right)\right]-{\lambda }_s\left({\lambda }_p+{\mu }_s\right)\left({\lambda }_p+{\mu }_p\right)\right\}}-\frac{1}{{\mu }_s}.$

证明 非优先权用户在各个状态下的到达率均为 ${\lambda }_s$ ，因此有效到达率 ${\lambda }_{s}q$ 。由little公式有 ${\lambda }_{eff}={\lambda }_s$ 。

$T_s\left(q\right)=\frac{N_s}{{\lambda }_{eff}}$ ， $T\left(q\right)=\frac{N}{{\lambda }_{eff}}$ 即可得到平均逗留时间和平均等待时间的表达式。

5. 双目标优化

本节建立了双目标优化问题，旨在同时优化系统成本和顾客的逗留时间。寻找使它们同时达到最优化的解集，并考虑他们之间的回归关系，进行回归分析。在本文所构建的模型中，对两类顾客的服务率是重要的参数，会影响整个系统的效率。因此，构建了预期逗留时间 $T\left({\mu }_p,\mu \right)$ 和成本函数 $C\left({\mu }_p,{\mu }_s\right)$ 。成本函数的具体表达式如下：

$C\left({\mu }_p,{\mu }_s\right)=C_{N}N+C_0{P}_0\left(1\right)+C_{1}P\left(1\right)+C_2{P}_2\left(1\right)+C_{{\mu }_p}{\mu }_p+C_{{\mu }_s}{\mu }_s$

其中，

$C_N$ ：表示每位顾客在系统中的单位时间成本；

$C_0$ ：表示系统处于空闲状态的单位时间成本；

$C_1$ ：表示系统为优先权顾客服务的单位时间成本；

$C_2$ ：表示系统为非优先权顾客服务的单位时间成本；

$C_{{\mu }_p}$ ：表示为优先权顾客服务期间服务率为提供的每个顾客的服务成本；

$C_{{\mu }_s}$ ：表示为非优先权顾客服务期间服务率为提供的每个顾客的服务成本。

该双目标优化问题表示如下：

$\underset{{\mu }_p>0,{\mu }_s>0}{\min }\left[C\left({\mu }_p,{\mu }_s\right),T\left({\mu }_p,{\mu }_s\right)\right],$

借助NSGA-II算法来寻找Pareto最优解集。其关键是找个各个目标函数之间的内在关系，找到使各个目标函数都达到最优的解集。在进行优化分析中，我们将参数取值为： ${\lambda }_p=0.3$ ， ${\lambda }_s=0.1$ ， $\theta =0.5$ ， $C_N=6$ ， $C_0=4$ ， $C_1=3$ ， $C_2=2$ ， $C_{{\mu }_p}=2$ ， $C_{{\mu }_s}=1$ ，并将 ${\mu }_p$ 和 ${\mu }_s$ 的取值限制为 $\left[1,4\right]$ 。表1给出了 ${\lambda }_s$ 取0.1，0.12，0.14时的Pareto最优解。只截取了部分数据展示在表1中。

Table 1. Pareto optimal solutions when λ s takes different values

表1. 取不同值的Pareto最优解

图2展示了不同 ${\lambda }_s$ 取值下，最优成本 $C_p$ 和最优逗留时间 $T_p$ 的关系图。从图中可以看出 $C_p$ 随着 ${\lambda }_s$ 的增大而增大。 $C_p$ 和 $T_p$ 成反比关系，图像形状类似负指数分布或对数分布。分别进行了建模和回归分析，发现负指数函数的拟合效果最优。

观察图3和图4可发现残差项近似服从正态分布。这意味着残差的正态性条件是满足的，可以建立各变量之间的回归关系。因此，建立多元回归模型如下：

$C_p={\beta }_0+{\beta }_1{\lambda }_s+{\beta }_2{T}_p+{\beta }_3{\text{e}}^{-T_p}.$

基于表1中的数据，使用加权最小二乘估计法得到各个参数的估计量。从表2中可以看出，在1%的显著性水平下，回归模型和各系数都通过了显著性检验。调整后的R²达到了99.6%，所选取的自变量可以解释因变量99.6%的变化，这表明模型的拟合效果较好。因此，可得回归方程如下：

$C_p=6.497+23.829{\lambda }_s+0.537T_p+21.587{\text{e}}^{-T_p}$

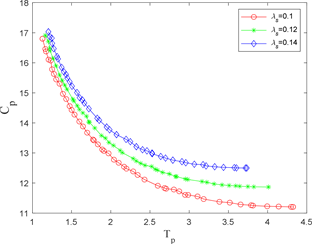
Figure 2. The trend chart of Pareto optimal solutions

图2. Pareto最优解走势图

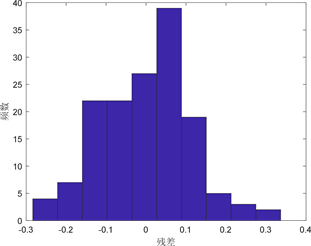
Figure 3. Histogram for the regression residuals

图3. 回归残差项直方图

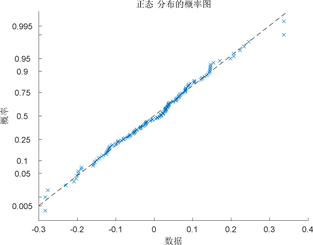
Figure 4. K-S test for the regression residuals

图4. 回归残差项的K-S检验

Table 2. Regression results

表2. 回归结果

从回归方程中可以看出， ${\lambda }_s$ 每变动一个单位， $C_p$ 平均变动23.829个单位； $T_p$ 每变动一个单位， $C_p$ 平均变动0.537个单位； ${\text{e}}^{-T_p}$ 每变动一个单位， $C_p$ 平均变动21.587个单位。同时我们可以发现，所有参数对 $C_p$ 的影响都是正向的，这是因为当 ${\lambda }_s$ 变大时，系统到达的顾客请求增加，必然会导致系统成本的增加。 $T_p$ 的估计值为正，这是因为顾客逗留时间的增加会导致系统成本的增加。回归模型的建立有助于系统管理者在顾客到达率确定的情况下，找到合适的两类顾客的服务率所需的最低成本。

6. 结论

本文考虑了基于抢占优先权和重试的M/M/1排队系统。利用概率生成函数的方法得到了模型的稳态概率，并且给出了系统的主要性能指标。然后借助NSGA-II算法来进行双目标优化，找到了同时使系统成本和顾客逗留时间的Pareto最优解集。最后以最优成本为因变量，非优先权顾客到达率，最优逗留时间和最优逗留时间的负指数为自变量建立了回归模型，并对模型进行了显著性检验。对系统管理者来说具有一定的参考价值。