求解一维双曲守恒律方程的高分辨率格式

A High-Resolution Scheme for Solving One-Dimensional Hyperbolic Conservation Law Equations

摘要: 对于双曲守恒律方程，当存在激波或间断时，熵相容格式会出现非物理振荡，为抑制振荡同时提高格式的分辨率，利用限制器构造高分辨率格式，对已有的sweby及MC限制器进行改进，将改进后的限制器添加至熵相容格式中。在一维双曲守恒律上进行数值实验结果表明，所构造的高分辨率熵相容格式具有鲁棒性、无振荡性等良好特性。

Abstract: For the hyperbolic conservation law equations, when shock waves or discontinuities are present, entropy-consistent schemes may exhibit non-physical oscillations. To suppress these oscillations and enhance the resolution of the scheme, high-resolution formats are constructed using limiters. We propose improvements to the existing Sweby and MC limiters and incorporate the enhanced limiters into the entropy-consistent scheme. Numerical experiments on one-dimensional hyperbolic conservation laws demonstrate that the developed high-resolution, entropy-consistent scheme ex-hibits robustness and freedom from oscillations, highlighting its favorable characteristics.

1. 引言

一维双曲守恒律方程的一般形式为

$u_t+f{\left(u\right)}_x=0$ , (1)

其中 $\left(x,t\right)\in R\times R^{+}$ ， $u:R\times R^{+}\to R^N\left(N\ge 1\right)$ 是守恒变量， $f\left(u\right)$ 是通量函数。双曲守恒律方程是计算流体力学中一类反映物理现象及其规律的重要方程，流体运动存在于人们日常生活中的各个领域，如航天航空、海洋、气象等领域都有广泛的应用。因此对该类方程数值求解方法的研究一直是一个很重要的课题。研究非线性双曲守恒律的主要困难是：即使初值函数光滑，其解在时间推进的某个时刻也可能会出现间断，产生激波、接触间断等。间断解的出现使双曲守恒律方程的解违背了古典解理论，于是Lax在1954年提出了弱解 [1] 的概念，允许间断解存在，这为数值方法更好的发展打下了良好的基础。但是由于弱解不惟一，1973年Lax从物理学中的热力学第二定律出发，在文献 [2] 中证明了熵稳定条件等价于这种“粘性消失”的机制，并由一个单元熵不等式来表示：

$E{\left(u\right)}_t+F{\left(u\right)}_x\le 0$ ， (2)

其中u是唯一的具有物理意义的解， $E\left(u\right)$ 是u的凸函数，满足 $E^{″}\left(u\right)>0$ ， $F\left(u\right)$ 是熵通量函数，满足上式的 $E\left(u\right)$ ， $F\left(u\right)$ 被称为熵对。为了满足熵稳定条件，同时避免非物理现象，长期以来的做法是引入额外的耗散来控制熵的变化。为合理地研究熵稳定与数值粘性之间的关系，1987年Tadmor在文献 [3] 里引入熵变量和熵势的概念，构造了一类二阶的熵守恒格式，其数值通量保持总熵不变。他还同时提出一种对数值粘性更精确量化的方法，即：一个三点格式只需含有比熵守恒格式更多的粘性则是熵稳定的。但是对于具体应该添加多少数值粘性一直以为都是研究人员值得思索的问题，Tadmor，Zhong [4] [5] 和Roe等在相关方面也做了许多工作，其中Roe所得到的熵稳定格式最为使用，被称为ERoe格式 [6] ，随后Roe和Ismail通过进一步分析得到：解在跨过激波时产生了激波强度立方量级的熵增，在此基础上发展了对数值粘性项更精确量化的熵相容格式 [7] ，熵相容格式是目前对熵的变化估计得最精确的一种熵稳定格式。但是熵相容格式只有一阶精度，且分辨率较低，因此本文将利用MUSCL [8] 重构方法构造斜率限制器以提高熵相容格式的分辨率。本文通过对已有的sweby [9] 及mc限制器 [10] 进行改进得到两类新的斜率限制器，应用在不同的双曲守恒律方程的数值求解，数值结果表明新格式具有稳健性、无振荡性等良好特征。

本文采用均匀网格上的半离散有限体积格式

$\frac{\text{d}}{\text{d}t}{\bar{u}}_j=-\frac{1}{\Delta x}\left(f_{j+1/2}-f_{j-1/2}\right)$ ，(3)

用 $\Delta x$ 表示空间步长， $\Delta t$ 表示时间步长，时间上采用三阶强Runge-Kutta方法 [11] ：

$u_i^{*}=u_i^k+\Delta tL\left(u_i^k\right)$ ， $u_i^{*}=\frac{3}{4}{u}_i^k+\frac{1}{4}{u}_i^{*}+\frac{\Delta t}{4}L\left(u_i^{*}\right)$ ， $u_i^{k+1}=\frac{1}{3}{u}_i^k+\frac{2}{3}{u}_i^{**}+\frac{2\Delta t}{3}L\left(u_i^{**}\right)$ 。 (4)

2. 斜率限制器的构造

考虑一维双曲守恒律方程

${\partial }_{t}u+{\partial }_{x}f\left(u\right)=0$ (5)

其中 $u=u\left(x,t\right)$ 是守恒变量， $f\left(u\right)$ 是光滑的通量函数。记 $u_i\left(x\right)$ 为每个控制单元 $I_i=\left[x_{i-1/2},x_{i+1/2}\right]$ 上的分段精确解，对每个 $u_i\left(x\right)$ 进行重构，重构后的函数表示为 $R_i\left(x\right)$ ，若 $\left|u_i\left(x\right)-R_i\left(x\right)\right|\le o\left({\left(\Delta x\right)}^{k+1}\right)$ ，则称重构后的函数 $R_i\left(x\right)$ 具有k-阶精度。 $u_i^n$ 表示在时间层 $t^n$ 上对控制单元 $I_i$ 的单元平均值，记为

$u_i^n=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{R}_i\left(x\right)\text{d}x}=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{u}_i\left(x\right)\text{d}x}$ (6)

在构造时，先将 $R_i\left(x\right)$ 在 $x_i$ 点处泰勒展开，得到

$R_i\left(x\right)=u_i\left(x_i\right)+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\frac{{\left(x-x_i\right)}^2}{2}+\cdots$ ， (7)

再将 $u_i\left(x\right)$ 在 $x_i$ 点处也进行泰勒展开，得到

$\begin{array}{c}{u}_i^n=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{u}_i\left(x\right)\text{d}x}=\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}\left[u_i\left(x_i\right)+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\frac{{\left(x-x_i\right)}^2}{2}+\cdots \right]\text{d}x}\\ =u_i\left(x_i\right)+0+\frac{1}{\Delta x}{\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}{\displaystyle {\int }_{I_i}\frac{{\left(x-x_i\right)}^2}{2}\text{d}x}+\cdots ,\end{array}$ (8)

联立(3)、(4)消去 $u_i\left(x_i\right)$ 得到

$R_i\left(x\right)=u_i\left(x_i\right)+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{1}{2}\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\left[{\left(x-x_i\right)}^2-\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{\left(x-x_i\right)}^2\text{d}x}\right]+\cdots$ 。 (9)

对上述式子取二阶重构得到

$R_i\left(x\right)=u_i\left(x_i\right)+{\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{1}{2}\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\left[{\left(x-x_i\right)}^2-\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{\left(x-x_i\right)}^2\text{d}x}\right]$ ， (10)

将上式简记为

$R_i\left(x\right)=u_i^n+H\left(x-x_i\right)$ ， (11)

其中

$H\left(x-x_i\right)={\frac{\partial u_i}{\partial x}|}_{x_i}\left(x-x_i\right)+{\frac{1}{2}\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}\left[{\left(x-x_i\right)}^2-\frac{1}{\Delta x}{\displaystyle {\int }_{I_i}{\left(x-x_i\right)}^2\text{d}x}\right]$ 。 (12)

为了方便，我们将对上式中的偏导数采用最简单的中心差分，即

${\frac{\partial u_i}{\partial x}|}_{x_i}=\frac{u_{i+1}^n-u_{i-1}^n}{2\Delta x}$ ， ${\frac{{\partial }^2{u}_i}{\partial x^2}|}_{x_i}=\frac{u_{i+1}^n-2u_i^n+u_{i-1}^n}{\Delta x^2}$ 。 (13)

本文将进一步对重构函数(11)进行限制，得到

$R_i\left(x\right)=u_i^n+\psi H\left(x-x_i\right)$ ， (14)

其中 $\psi \in \left[0,1\right]$ 是一个斜率限制器。为了能够构造一个既具有superbee限制器分辨率同时又能避免伪振荡的限制器，现对已有的sweby限制器和mc限制器进行改进构造两类新的限制器，具体构造方法如下：

1) 对sweby限制器 [9]

${\psi }_{sw}\left(r\right)=\max \left[0,\min \left(\beta r,1\right),\min \left(r,\beta \right)\right],\beta \in \left(1,2\right)$ (15)

进行改进得到

${\psi }_{m\text{-}sw}\left(r\right)=\max \left[0,\min \left(\beta r,1/r\right),\min \left(r,\beta \ast 1/r\right)\right],\beta \in \left(1,2\right)$ (16)

将新的限制器记作m-sweby限制器，当 $\beta \to 1$ 时，记作

${\psi }_{m\text{-}mm}\left(r\right)=\max \left[0,\min \left(1/r,r\right)\right]$ (17)

${\psi }_{m\text{-}mm}$ 可看作是对已有的minmod限制器 ${\psi }_{mm}\left(r\right)=\max \left[0,\min \left(1,r\right)\right]$ 的改进。当 $\beta \to 2$ 时，记作

${\psi }_{m\text{-}sb}\left(r\right)=\max \left[0,\min \left(2r,1/r\right),\min \left(r,2\ast 1/r\right)\right]$ (18)

${\psi }_{m\text{-}sb}$ 可看作是对已有的superbee限制器 ${\psi }_{sb}\left(r\right)=\max \left[0,\min \left(1,2r\right),\min \left(2,r\right)\right]$ 的改进。

2) 对mc限制器 [10]

${\psi }_{mc}\left(r\right)=\max \left(0,\min \left(2r,0.5\left(1+r\right),2\right)\right)$ ， (19)

进行改进得到

${\psi }_{m-mc}\left(r\right)=\max \left(0,\min \left(2r,0.5\left(1/r+r\right),2/r\right)\right)$ 。 (20)

将新的限制器记作m-mc限制器。

3. 高分辨率熵相容格式

3.1. 传统数值格式

3.1.1. 熵守恒格式

考虑一维双曲守恒律方程

${\partial }_{t}u+{\partial }_{x}f\left(u\right)=0$ (21)

其中 $u=u\left(x,t\right)$ 是守恒变量， $f\left(u\right)$ 是光滑的通量函数。

熵守恒格式能够保持总熵不变，在离散条件下满足单元熵等式

$\frac{\text{d}}{\text{d}t}U\left(u_i\left(t\right)\right)+\frac{1}{\Delta x}\left(F_{i+1/2}-F_{i-1/2}\right)=0$ (22)

其中 $U\left(u_i\left(t\right)\right)$ 为凸的熵函数， $F_{i+1/2}$ 为数值熵通量函数。对于给定熵对 $\left(U,F\right)$ ，熵变量为 $v=U_u$ ，熵势为 $\psi =v^{\text{T}}f-F$ 满足条件 $f=\partial \psi /\partial v$ 。则熵守恒通量 $f_{i+1/2}^c$ 可以写成沿熵变量空间内路径

$v_{j+1/2}\left(\xi \right)=\frac{1}{2}\left(v_j+v_{j+1}\right)+\xi \left(v_{j+1}-v_j\right)$ (23)

的积分形式

$f_{i+1/2}^c={\displaystyle {\int }_{\xi =-1/2}^{1/2}f\left(v_{j+1/2}\left(\xi \right)\right)\text{d}\xi }$ ， (24)

Tadmor在文献 [12] [13] 中由该积分形式出发推导出数值通量满足熵守恒条件

${\left(v_{j+1}-v_j\right)}^{\text{T}}{f}_{i+1/2}^c=\psi \left(v_{j+1}\right)-\psi \left(v_j\right)$ (25)

当计算标量情况下的双曲守恒律方程时，熵守恒通量沿空间内的路径只有直线形式，因此熵守恒通量 $f_{i+1/2}^c$ 具有惟一表达形式

$f_{i+1/2}^c=\frac{{\left[\psi \right]}_{i+1/2}}{{\left[v\right]}_{i+1/2}}=\frac{{\psi }_{i+1}-{\psi }_i}{v_{i+1}-v_i}$ ， (26)

3.1.2. 熵相容格式

熵守恒格式能够保持总熵不变，在光滑区域具有良好的表现且具有二阶精度，但是当间断解出现时熵会增加，使得熵守恒格式的数值解会出现伪振荡，因此为满足熵稳定，总熵必须进行耗散。通过在熵守恒的基础上添加Roe-耗散项

$D_{i+1/2}^{ES}=\frac{1}{2}{R}_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[v\right]}_{i+1/2}$ ， (27)

其中 $\left|{\Lambda }_{i+1/2}\right|=diag\left(\left|{\lambda }_{i+1/2}^1\right|,\cdots ,\left|{\lambda }_{i+1/2}^N\right|\right)$ 是 $A\left(u\right)=\frac{\text{d}f}{\text{d}u}$ 的特征值矩阵，R是 $A\left(u\right)=\frac{\text{d}f}{\text{d}u}$ 的右特征向量，得到熵稳定格式的数值通量 $f_{i+1/2}^{ES}$

$f_{i+1/2}^{ES}=f_{i+1/2}^C-D_{i+1/2}^{ES}=f_{i+1/2}^C-\frac{1}{2}{R}_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[v\right]}_{i+1/2}$ ， (28)

与熵守恒格式相比，熵稳定格式只多了耗散项 $D_{i+1/2}^{ES}$ ，但是这个耗散项不足以抵消跨越激波所产生的熵增，因此在数值实验中，该耗散项在激波附近仍然可能出现伪振荡。于是Roe和Ismail进一步分析跨越激波处的熵增，得到了对熵的变化估计更精确的熵相容通量

$\begin{array}{c}{f}_{i+1/2}^{EC}=f_{i+1/2}^C-D_{i+1/2}^{ES}-D_{i+1/2}^{EP}\\ \approx f_{i+1/2}^C-\frac{1}{2}{R}_{i+1/2}\left(\left|{\Lambda }_{i+1/2}\right|+\left|{\displaystyle \underset{k=1}{\overset{q}{\sum }}{w}_k\left(2S_k-1\right)\Lambda \left(u\left(S_k\right)\right)}\right|\right)R_{i+1/2}^{\text{T}}{\left[v\right]}_{i+1/2}\end{array}$ (29)

其中 $S_{1,3}=\frac{1}{2}\pm \frac{\sqrt{15}}{10}$ ， $S_2=\frac{1}{2}$ ， $w_{1,3}=\frac{5}{9}$ ， $w_2=\frac{8}{9}$ ，记 $D_{i+1/2}=\left|{\Lambda }_{i+1/2}\right|+\left|{\displaystyle \underset{k=1}{\overset{q}{\sum }}{w}_k\left(2S_k-1\right)\Lambda \left(u\left(S_k\right)\right)}\right|$ ，则上式可简化为

$f_{i+1/2}^{EC}=f_{i+1/2}^C-\frac{1}{2}{R}_{i+1/2}\left|D_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[v\right]}_{i+1/2}$ (30)

在标量情况下，熵相容格式的数值通量为

$\begin{array}{c}{f}_{i+1/2}^{EC}=f_{i+1/2}^C-D_{i+1/2}^{ES}-D_{i+1/2}^{EP}\\ =f_{i+1/2}^C-\frac{1}{2}\left|a\left(u_{i+1/2}\right)\right|{\left[v\right]}_{i+1/2}-\frac{1}{2}\left|{\displaystyle {\int }_0^1\left(2\xi -1\right)a\left(u\left(\xi \right)\right)U_{uu}\left(\xi \right)\text{d}\xi }\right|{\left[v\right]}_{i+1/2}\end{array}$ (31)

其中 $a\left(u\right)$ 是特征速度，记 $D_{i+1/2}=\left|a\left(u_{i+1/2}\right)\right|+\left|{\displaystyle {\int }_0^1\left(2\xi -1\right)a\left(u\left(\xi \right)\right)U_{uu}\left(\xi \right)\text{d}\xi }\right|$ ，则上式可简化为

$f_{i+1/2}^{EC}=f_{i+1/2}^C-\frac{1}{2}{D}_{i+1/2}{\left[v\right]}_{i+1/2}$ (32)

3.1.3. 高分辨率熵相容格式

将本文所设计的斜率限制器应用于上述标量熵相容格式中得到高分辨率熵相容格式，一维标量情况下的高分辨率熵相容格式的数值通量为

$f_{i+1/2}^{EC\text{-}Limited}=f_{i+1/2}^C-\frac{1}{2}{D}_{i+1/2}{\left[v\right]}_{i+1/2}^{Limited}$ , (33)

其中 ${\left[v\right]}_{i+1/2}^{Limited}=v_i^R-v_i^L$ 。 $v_i^L$ ， $v_i^R$ 可由3.1.1节的方法得出。在一维标量双曲守恒律方程中，上述的构造方法是先将守恒变量u转化为原始变量重构，再将重构后的值代入熵变量，最终得到高分辨率熵相容格式的数值通量 $f_{i+1/2}^{EC\text{-}Limited}$ 。

对于一维标量burgers方程

$u_t+f{\left(u\right)}_x=0$ ， (34)

其中， $f\left(u\right)=u^2/2$ ，熵函数为 $E\left(u\right)=u^2/2$ ，熵通量函数为 $F\left(u\right)=2u^2/3$ ，特征值为 $a\left(u\right)=u$ ，进而得到熵变量 $v\left(u\right)=E^{\prime }\left(u\right)=u$ ，熵势 $\psi \left(u\right)=v\left(u\right)f\left(u\right)-F\left(u\right)=u^3/6$ ，由式(26)可得出burgers方程的熵守恒数值通量为 $f_{j+1/2}^c=\left(u_j^2+u_j{u}_{j+1}+u_{j+1}^2\right)/6$ ，最终得到burgers方程的熵稳定数值通量和熵相容数值通量分别为

$f_{i+1/2}^{ES}=f_{i+1/2}^C-\frac{1}{4}\left|u_i+u_{i+1}\right|\left(u_{i+1}-u_i\right)$ ；(35)

$f_{i+1/2}^{EC}=f_{i+1/2}^c-\frac{1}{2}\left(\frac{1}{2}\left|u_i+u_{i+1}\right|+\frac{1}{6}\left|u_{i+1}-u_i\right|\right)\left(u_{i+1}-u_i\right)$ 。 (36)

3.2. 一维浅水波方程

考虑描述浅水情况下流体运动规律的浅水波方程，具有以下守恒格式：

$\frac{\partial }{\partial t}\left[\begin{array}{c}h\\ uh\end{array}\right]+\frac{\partial }{\partial x}\left[\begin{array}{c}hu\\ g{h}^2/2+h{u}^2\end{array}\right]=0$ ， (37)

其中h是水深，u是速度，g是重力加速度，取熵函数 $E\left(u\right)=\left(g{h}^2+u^{2}h\right)/2$ ，熵通量为 $F=h{u}^3/2+gu{h}^2$ ，熵变量为 $v=E^{\prime }\left(u\right)={\left[gh-u^2/2,u\right]}^{\text{T}}$ 。熵守恒的数值通量采用Fjordholm在文献 [14] 所提出的潜水波方程的显式熵守恒格式的数值通量：

$F_{i+1/2}^c=\left(\begin{array}{c}{\bar{h}}_{i+1/2}{\bar{u}}_{i+1/2}\\ \frac{g}{2}{\left({\bar{h}}^2\right)}_{i+1/2}+{\bar{h}}_{i+1/2}{\left({\bar{u}}_{i+1/2}\right)}^2\end{array}\right)$ 。 (38)

其中 $\overline{(\cdot )}=\left({(\cdot )}_i+{(\cdot )}_{i+1}\right)/2$ ， $\overline{{(\cdot )}^2}=\left({(\cdot )}_i^2+{(\cdot )}_{i+1}^2\right)/2$ 。

最终得到潜水波方程的熵稳定格式和熵相容格式的数值通量分别为

$f_{i+1/2}^{ES}=f_{i+1/2}^C-\frac{1}{2}{R}_{i+1/2}\left|{\Lambda }_{i+1/2}\right|R_{i+1/2}^{\text{T}}{\left[v\right]}_{i+1/2}$ ， (39)

$f_{i+1/2}^{ES}=f_{i+1/2}^C-\frac{1}{2}{R}_{i+1/2}\left(\left|{\Lambda }_{i+1/2}\right|+\left|{\displaystyle \underset{k=1}{\overset{q}{\sum }}{w}_k\left(2S_k-1\right)\Lambda \left(u\left(S_k\right)\right)}\right|\right)R_{i+1/2}^{\text{T}}{\left[v\right]}_{i+1/2}$ ， (40)

对应雅可比矩阵的特征值矩阵为

$\Lambda =\left[\begin{array}{cc}u-\sqrt{gh}& \\ & u+\sqrt{gh}\end{array}\right]$ 。 (41)

使用Roe平均值计算的平均特征值和特征向量矩阵为

${\Lambda }_{i+1/2}=\left[\begin{array}{cc}\bar{u}-\sqrt{g\bar{h}}& \\ & \bar{u}+\sqrt{g\bar{h}}\end{array}\right]$ ， $R_{i+1/2}=\frac{1}{\sqrt{2g}}\left[\begin{array}{cc}1& 1\\ \bar{u}-\sqrt{g\bar{h}}& \bar{u}+\sqrt{g\bar{h}}\end{array}\right]$ 。 (42)

4. 数值算例

对熵稳定格式,熵相容格式与构造的高分辨率熵相容格式进行数值模拟，通过数值结果说明所构造的高分辨率熵相容格式具有良好的性质。

符号约定：

ES：熵稳定格式；EC：熵相容格式；EC-Limited1：添加m-sweby限制器的高分辨率熵相容格式；EC-Limited2：添加m-mc限制器的高分辨率熵相容格式；Exact：参考解。

4.1. 一维Burgers方程

对于一维burgers方程的不同初值问题，在下面的实验中均采取60网格进行计算。

4.1.1. 稀疏波问题

在区域[−0.5, 0.5]上求解初值问题

$u\left(x,0\right)=\{\begin{array}{ll}-1,\hfill & \text{if}x<0,\hfill \\ 1,\hfill & \text{if}x\ge 0,\hfill \end{array}$

计算至 $t=0.25$ ，这个问题的精确解是一个稀疏波

$u\left(x,0\right)=\{\begin{array}{ll}sign\left(t\right),\hfill & \text{if}\left|x\right|>t,\hfill \\ x/t,\hfill & \text{if}\left|x\right|\le t,\hfill \end{array}$

此时令 $\beta =2$ ，计算结果与参考解如图1所示。数值结果表明EC格式比ES格式具有更高的分辨率，但是ES格式与EC格式在稀疏波区域的音速点处仍然会产生膨胀激波，EC-Limited1及EC-Limited2格式均可以消除稀疏波附近的伪振荡、提高格式的分辨率同时可以消除膨胀激波，提高计算结果的精确度。

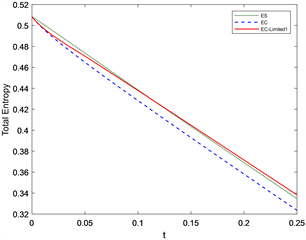
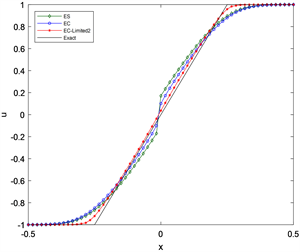
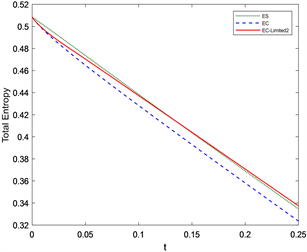
Figure 1. Numerical results of sparse wave problem for Burgers equation

图1. Burgers方程稀疏波问题的数值结果

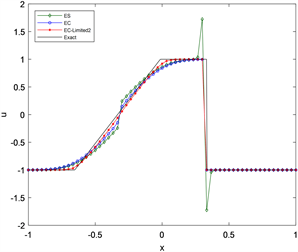
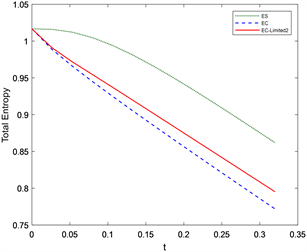
Figure 2. Numerical results of the discontinuous initial value problem for the Burgers equation

图2. Burgers方程间断初值问题的数值结果

4.1.2. 间断初值问题

在区间[−1, 1]上求解初值问题

$u\left(x,0\right)=\{\begin{array}{ll}-1,\hfill & \text{if}\frac{1}{3}\le \left|x\right|\le 1,\hfill \\ 1,\hfill & \text{if}\left|x\right|<\frac{1}{3},\hfill \end{array}$

计算至t = 0.32，CFL条件数取为0.8，令 $\beta =2$ ，如图2所示，观察数值结果和参考解，可以看出EC-Limited1及EC-Limited2格式具有更好的计算效果，能够准确的捕捉激波和稀疏波，并消除伪振荡。从熵耗散图可以看出EC-Limited1及EC-Limited2格式的熵耗散介于两者之间，既提高了格式的稳定性，同时提高了计算结果的准确性。

4.2. 一维浅水波方程

4.2.1. 考虑在区间[0, 1]溃坝问题

设初始条件为

$h\left(x,0\right)=\{\begin{array}{ll}10\hfill & x<0.5\hfill \\ 5\hfill & x\ge 0.5\hfill \end{array}$ ， $u\left(x,0\right)=0$

取200个网格点，计算至t = 0.05，条件数取为0.2，令 $\beta =1.5$ ，数值结果和参考解如图3所示，由图3可以看出：浅水波方程的熵相容格式具有明显的抹平作用，而EC-Limited1及EC-Limited2格式在计算激波和稀疏波时，都能得到较好的计算结果。

4.2.2. 高度接近0的溃坝问题

给定初始条件

$h\left(x,0\right)=1$ ， $u\left(x,0\right)=\{\begin{array}{ll}-4,\hfill & x<0,\hfill \\ 4,\hfill & x>0,\hfill \end{array}$

使用Neumann边界条件。

1) 在区域[−0.5, 0.5]上计算至t₁ = 0.0056，取网格数N = 300， $\beta =2$ ，结果如图4所示。

2) 在区域[−1, 1]上计算至t₂ = 0.1，取网格数N = 200， $\beta =2$ ，结果如图5所示。

该问题的解是在水流中间产生一个凹陷，在凹陷两侧均为稀疏波。值得注意，在解决该问题时，水深可以接近0，但不能产生负值。在图4、图5的数值计算结果中，EC-Limited1及EC-Limited2格式对间断的捕捉更好，计算结果更优。

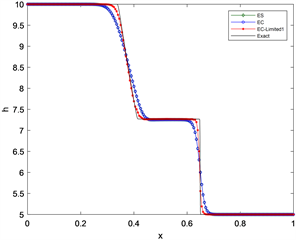
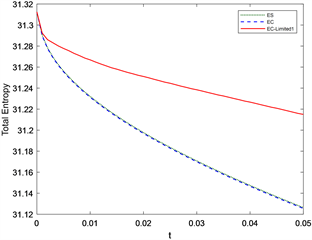
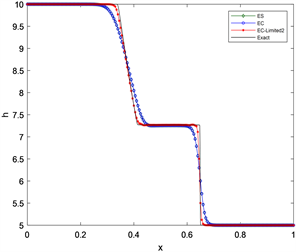
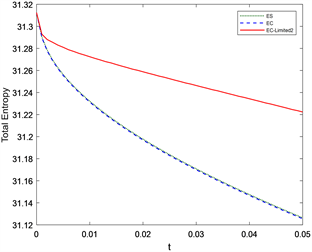
Figure 3. Numerical results of shallow water wave equation dam failure problem

图3. 浅水波方程溃坝问题的数值结果

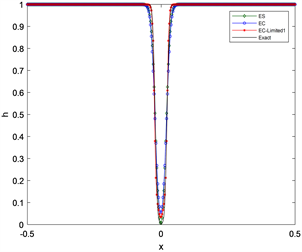
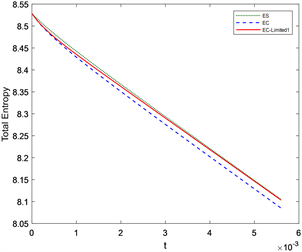
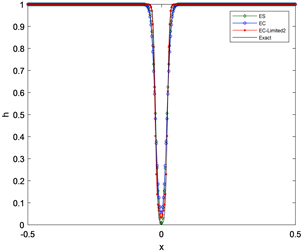
Figure 4. Dam failure problem with shallow water wave equation height approaching zero, t₁ = 0.0056

图4. 浅水波方程高度接近零的溃坝问题，t₁ = 0.0056

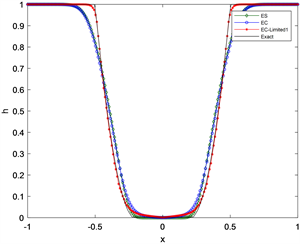
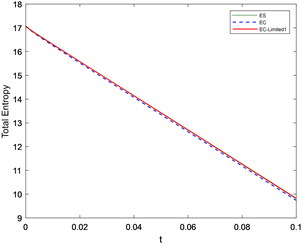
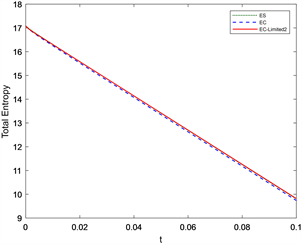
Figure 5. Dam failure problem with height close to zero in one-dimensional shallow water wave equation, t₁ = 0.1

图5. 一维浅水波方程高度接近零的溃坝问题，t₁ = 0.1

5. 结论

本文对一维双曲守恒律方程，通过限制器机制对已有的sweby及mc限制器进行改进，并将改进的限制器添加至熵相容格式中，最终得到高分辨率熵相容格式。数值结果表明，该格式具有高分辨率、无振荡等良好性质，在一维情况下，EC-Limited1格式针对激波较强或稀疏波较强等不同的情形，需要对 $\beta$ 取不同的值。

NOTES

^*通讯作者。