二维预泊松代数的分类

Classification of 2-Dimensional Pre-Poisson Algebras

摘要: 本文主要研究低维预泊松代数的分类，以二维Zinbiel代数的分类为基础，计算低维预泊松代数上的预李代数的左乘运算在某组基下对应的矩阵，确定了对应的预李代数的类型。最后，通过具体计算得到了预泊松代数的同构关系，从而得到了二维预泊松代数的分类。

Abstract: This paper mainly studies the classification of low-dimensional pre-poisson algebras. Based on the classification of two-dimensional Zinbiel algebras, the matrix corresponding to the left multiplica-tion operation of the pre-poisson algebras on the low-dimensional pre-poisson algebras is calculated under a certain set of bases, and the type of the corresponding pre-poisson algebras is determined. Finally, the isomorphic relation of pre-poisson algebras is obtained through concrete calculation, and the classification of two-dimensional pre-poisson algebras is obtained.

1. 引言

泊松代数起源于20世纪70年代对泊松几何的研究，并出现在数学和物理学的极其广泛的领域，如泊松流形、量子化理论、量子群等。预泊松代数和泊松代数有着密切的联系。在1999年，Aguiar引入了预泊松代数的概念 [1] ，即一个预泊松代数包含一个Zinbiel代数和一个满足相容条件的预李代数。由于代数分类(直至同构)是非结合代数理论中的一个经典问题，而泊松代数、Zinbiel代数和预李代数的分类已经分别在 [2] [3] [4] 中给出，本文主要考虑在此分类的基础上研究二维预泊松代数的分类。

2. 预备知识

定义1.1 [5] 设A是复数域上的向量空间，A上具有双线性运算，若 $\left(A,\cdot \right)$ 是交换结合代数， $\left(A,\left[,\right]\right)$ 是李代数，且满足相容条件

$\left[x,y\cdot z\right]=\left[x,y\right]\cdot z+y\cdot \left[x,z\right],\forall x,y,z\in A$ ,

则称三元组 $\left(A,\cdot ,\left[,\right]\right)$ 为泊松代数。

定义1.2 [6] 设A是复数域上的向量空间，且有双线性运算 $\ast :A\times A\to A$ ，若 $\ast$ 满足

$x\ast \left(y\ast z\right)=\left(y\ast x\right)\ast z+\left(x\ast y\right)\ast z,\forall x,y,z\in A$ ,

则称 $\left(A,\ast \right)$ 为Zinbiel代数。

定义1.3 [7] 设A是复数域上的向量空间，且有双线性运算 $\circ$ ，若 $\circ$ 满足

$x\circ \left(y\circ z\right)-\left(x\circ y\right)\circ z=y\circ \left(x\circ z\right)-\left(y\circ x\right)\circ z,\forall x,y,z\in A$ ,

则称 $\left(A,\circ \right)$ 为预李代数。

定义1.4 [1] 设A是复数域上的向量空间， $\ast ,\circ$ 是A上的双线性运算，如果 $\left(A,\ast \right)$ 是Zinbiel代数， $\left(A,\circ \right)$ 是预李代数，且满足

$\left(x\circ y-y\circ x\right)\ast z=x\circ \left(y\ast z\right)-y\ast \left(x\circ z\right)$ , (1.1)

$\left(x\ast y+y\ast x\right)\circ z=x\ast \left(y\circ z\right)+y\ast \left(x\circ z\right)$ , (1.2)

其中 $x,y,z\in A$ ，则称 $\left(A,\ast ,\circ \right)$ 为预泊松代数。

设 $\left(A,\ast ,\circ \right)$ 是预泊松代数， $L_{\ast },R_{\ast }$ 分别为A关于 $\ast$ 的左乘，右乘运算，其中

$L_{\ast }\left(x\right)y=x\ast y,R_{\ast }\left(x\right)y=y\ast x,\forall x,y\in A$ .

同理可定义A关于 $\circ$ 的左乘，右乘运算，设 $L_{\circ },R_{\circ }$ 分别为A关于 $\circ$ 的左乘，右乘运算，其中

$L_{\circ }\left(x\right)y=x\circ y,R_{\circ }\left(x\right)y=y\circ x,\forall x,y\in A$ .

定义1.5设 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 与 $\left(A_2,{\ast }_2,{\circ }_2\right)$ 是泊松代数， $\phi :A_1\to A_2$ 为线性映射，若 $\phi$ 满足

$\phi \left(x{\ast }_{1}y\right)=\phi \left(x\right){\ast }_2\phi \left(y\right),\phi \left(x{\circ }_{1}y\right)=\phi \left(x\right){\circ }_2\phi \left(y\right),\forall x,y\in A$ ,

则称 $\phi$ 为 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 到 $\left(A_2,{\ast }_2,{\circ }_2\right)$ 的同态映射。

特别地，若 $\phi$ 为双射，则称 $\phi$ 为 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 和 $\left(A_2,{\ast }_2,{\circ }_2\right)$ 的同构映射。显然，若两个泊松代数 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 和 $\left(A_2,{\ast }_2,{\circ }_2\right)$ 同构，则作为Zinbiel代数，和 $\left(A_2,{\ast }_2\right)$ 同构，作为预李代数， $\left(A_1,{\circ }_1\right)$ 和 $\left(A_2,{\circ }_2\right)$ 同构。

定理1 [8] 若A为二维Zinbiel代数，则存在A的一组基 $e_1,e_2$ ，满足 $e_1\ast e_1=e_2$ 。

定理2 [4] 设A是复数域上的二维左对称代数，则A一定同构于下面的(互不同构)左对称代数：

$A^1=\langle e_1,e_2|e_i{e}_j={\delta }_{ij}{e}_i,i,j=1,2\rangle ;$

$A^2=\langle e_1,e_2|e_1{e}_1=e_1,e_1{e}_2=e_2{e}_1=e_2,e_2{e}_2=0\rangle ;$

$A^3=\langle e_1,e_2|e_1{e}_1=e_1,e_1{e}_2=e_2{e}_1=e_2{e}_2=0\rangle ;$

$A^4=\langle e_1,e_2|e_1{e}_1=e_1=e_1{e}_2=e_2{e}_1=e_2{e}_2=0\rangle ;$

$A^5=\langle e_1,e_2|e_1{e}_1=e_2,e_1{e}_2=e_2{e}_1=e_2{e}_2=0\rangle ;$

$A^6=\langle e_1,e_2|e_1{e}_1=e_1{e}_2=0,e_2{e}_1=-e_1,e_2{e}_2=-e_2\rangle ;$

$A^7\in \left\{A_k|A_k=\langle e_1,e_2|e_1{e}_1=e_1{e}_2=0,e_2{e}_1=-e_1,e_2{e}_2=k{e}_2\rangle ,k\ne -1\right\};$

$A_{-1}=\langle e_1,e_2|e_1{e}_1=e_1{e}_2=0,e_2{e}_1=-e_1,e_2{e}_2=e_1-e_2\rangle ;$

$A^8=\langle e_1,e_2|e_1{e}_1=0,e_1{e}_2=e_1,e_2{e}_1=0,e_2{e}_2=e_2\rangle ;$

$A^9\in \left\{A_l|A_l=\langle e_1,e_2|e_1{e}_1=0,e_1{e}_2=l{e}_1,e_2{e}_1=\left(l-1\right)e_1,e_2{e}_2=e_1+l{e}_2\rangle ,l\ne 0\right\};$

$A^{10}=\langle e_1,e_2|e_1{e}_1=2e_1,e_1{e}_2=e_2,e_2{e}_1=0,e_2{e}_2=e_1\rangle .$

3. 二维预泊松代数上关于预李代数的左乘运算

定理3 设 $\left(A,\ast ,\circ \right)$ 是二维预泊松代数，则存在A的一组基 $e_1,e_2$ ，有 $e_1\ast e_1=e_2$ ，且满足

$e_1\circ e_1=\lambda e_1+\mu e_2,e_1\circ e_2=e_2\circ e_1=\lambda e_2$ ,

其中 $\lambda ,\mu \in ℂ$ 。

证 由定理1可知，存在A的一组基 $e_1,e_2$ 使 $e_1\ast e_1=e_2$ ，从而关于 $\ast$ 的左乘运算 $L_{\ast }\left(e_1\right),L_{\ast }\left(e_2\right)$ 在 $e_1,e_2$ 下对应的矩阵为

$L_{\ast }\left(e_1\right)=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right),L_{\ast }\left(e_2\right)=0$ .

设关于 $\circ$ 的左乘运算 $L_{\circ }\left(e_1\right),L_{\circ }\left(e_2\right)$ 在 $e_1,e_2$ 下对应的矩阵为

$L_{\circ }\left(e_1\right)=\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_4\end{array}\right),L_{\circ }\left(e_2\right)=\left(\begin{array}{cc}{b}_1& b_2\\ b_3& b_4\end{array}\right),a_i,b_i\in ℂ,i=1,2,3,4.$

根据预泊松代数的定义，由(1.1) (1.2)知关于 $\circ$ 的左乘运算需要满足的条件是：

$L_{\circ }\left(x\ast y+y\ast x\right)=L_{\ast }\left(x\right)L_{\circ }\left(y\right)+L_{\ast }\left(y\right)L_{\circ }\left(x\right)$ , (2.1)

$L_{\ast }\left(x\circ y+y\circ x\right)=L_{\circ }\left(x\right)L_{\ast }\left(y\right)+L_{\ast }\left(y\right)L_{\circ }\left(x\right)$ . (2.2)

一方面，在等式(2.1)中，分别考虑 $x,y$ 取基 $e_1,e_2$ ，有下列4种情况：

(1) 若 $x=e_1,y=e_1$ ，有

$L_{\circ }\left(2e_1\ast e_1\right)=2L_{\circ }\left(e_2\right)=2L_{\ast }\left(e_1\right)L_{\circ }\left(e_1\right)$ ,

即

$\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_4\end{array}\right)=\left(\begin{array}{cc}{b}_1& b_2\\ b_3& b_4\end{array}\right)$ ,

通过计算可得

$\left(\begin{array}{cc}0& 0\\ a_1& a_2\end{array}\right)=\left(\begin{array}{cc}{b}_1& b_2\\ b_3& b_4\end{array}\right)$ .

即

$b_1=b_2=0,b_3=a_1,b_4=a_2$ .

(2) 若 $x=e_1,y=e_2$ ，有

$L_{\circ }\left(e_1\ast e_2+e_2\ast e_1\right)=L_{\ast }\left(e_1\right)L_{\circ }\left(e_2\right)+L_{\ast }\left(e_2\right)L_{\circ }\left(e_1\right)$ ,

即

$0=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)\left(\begin{array}{cc}0& 0\\ a_1& a_2\end{array}\right)$ .

通过计算得对任意 $a_1,a_2$ 等式恒成立。

(3) 若 $x=e_2,y=e_1$ ，有

$L_{\circ }\left(e_2\ast e_1+e_1\ast e_2\right)=L_{\ast }\left(e_2\right)L_{\circ }\left(e_1\right)+L_{\ast }\left(e_1\right)L_{\circ }\left(e_2\right)$ ,

即

$0=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)\left(\begin{array}{cc}0& 0\\ a_1& a_2\end{array}\right)$ .

通过计算得对任意 $a_1,a_2$ ，等式恒成立。

(4) 若 $x=e_2,y=e_2$ ，有

$0=L_{\circ }\left(2e_2\ast e_2\right)=2L_{\ast }\left(e_2\right)L_{\circ }\left(e_2\right)$ .

由 $L_{\ast }\left(e_2\right)=0$ 可知等式恒成立。

在等式(2.2)中，分别考虑 $x,y$ 取基 $e_1,e_2$ ，有下列4种情况：

(1) 若 $x=e_1,y=e_1$ ，有

$0=L_0\left(e_1\right)L_{\ast }\left(e_1\right)-L_{\ast }\left(e_1\right)L_0\left(e_1\right)$ ,

即

$0=\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_4\end{array}\right)\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)-\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)\left(\begin{array}{cc}{a}_1& a_2\\ a_3& a_4\end{array}\right)=\left(\begin{array}{cc}{a}_2& 0\\ a_4-a_1& -a_2\end{array}\right)$ ,

计算得

$a_2=0,a_1=a_4$ .

(2) 若 $x=e_1,y=e_2$ ，有

$0=L\ast \left(e_1\circ e_2-e_2\circ e_1\right)=L_{\circ }\left(e_1\right)L_{\ast }\left(e_2\right)-L_{\ast }\left(e_2\right)L_{\circ }\left(e_1\right)$ ,

由 $L_{\ast }\left(e_2\right)=0$ 可知等式恒成立。

(3) 若 $x=e_2,y=e_1$ ，有

$0=L_{\ast }\left(e_2\circ e_1-e_1\circ e_2\right)=L_{\circ }\left(e_2\right)L_{\ast }\left(e_1\right)-L_{\ast }\left(e_1\right)L_{\circ }\left(e_2\right)$ ,

通过计算得

$\left(\begin{array}{cc}0& 0\\ a_2& 0\end{array}\right)=0$ .

即 $a_2=0$ 。

(4) 若 $x=e_2,y=e_2$ ，有

$0=L_0\left(e_2\right)L_{\ast }\left(e_2\right)-L_{\ast }\left(e_2\right)L_0\left(e_2\right)$ .

由 $L_{\ast }\left(e_2\right)=0$ 可知等式恒成立。

此时有

$e_1\circ e_1=a_1{e}_1+a_2{e}_2,e_1\circ e_2=a_1{e}_2,e_2\circ e_1=a_1{e}_2,e_2{e}_2=0$ .

另一方面，根据预李代数的定义，关于 $\circ$ 的左乘运算还需要满足条件：

$L_{\circ }\left(x\circ y-y\circ x\right)=L_{\circ }\left(x\right)L_{\circ }\left(y\right)-L_{\circ }\left(y\right)L_{\circ }\left(x\right)$ . (2.3)

在等式(2.3)中，分别考虑 $x,y$ 取基 $e_1,e_2$ ，有下列4种情况：

(1) 若 $x=e_1,y=e_1$ ，有

$0=L_{\circ }\left(e_1\circ e_1-e_1\circ e_1\right)=L_{\circ }\left(e_1\right)L_{\circ }\left(e_1\right)-L_{\circ }\left(e_1\right)L_{\circ }\left(e_1\right)$ .

(2) 若 $x=e_1,y=e_2$ ，有

$a_1^2=L_{\circ }\left(e_1\circ e_2-e_2\circ e_1\right)=L_{\circ }\left(e_1\right)L_{\circ }\left(e_2\right)-L_{\circ }\left(e_2\right)L_{\circ }\left(e_1\right)$ .

(3) 若 $x=e_2,y=e_1$ ，有

$a_1^2=L_{\circ }\left(e_2\circ e_1-e_1\circ e_2\right)=L_{\circ }\left(e_2\right)L_{\circ }\left(e_1\right)-L_{\circ }\left(e_1\right)L_{\circ }\left(e_2\right)$ .

(4) 若 $x=e_2,y=e_2$ ，有

$0=L_{\circ }\left(e_2\circ e_2-e_2\circ e_2\right)=L_{\circ }\left(e_2\right)L_{\circ }\left(e_2\right)-L_{\circ }\left(e_2\right)L_{\circ }\left(e_2\right)$ .

通过计算，以上4个方程对任意 $a_1,a_2$ ，等式恒成立。综上，可知

$e_1\circ e_1=a_1{e}_1+a_3{e}_2\text{,}{e}_1\circ e_2=a_1{e}_2\text{,}{e}_2\circ e_1=a_1{e}_2$ .

取 $\lambda =a_1,\mu =a_3$ ，则对于A的基 $e_1,e_2$ ，满足

$e_1\circ e_1=\lambda e_1+\mu e_2\text{,}{e}_1\circ e_2=e_2\circ e_1=\lambda e_2$ ,

其中 $\lambda ,\mu \in ℂ$ 。

4. 二维预泊松代数的类型

定理4 设 $\left(A,\ast ,\circ \right)$ 是二维预泊松代数， $e_1,e_2$ 为A的基，则 $\left(A,\ast ,\circ \right)$ 中的运算 $\circ$ 为以下几种类型：

(1) $e_1\circ e_1=e_1\circ e_2=e_2\circ e_1=e_2\circ e_2=0$ ， $\left(A,\circ \right)$ 同构于A⁴型的预李代数；

(2) $e_1\circ e_1=\lambda e_1,e_1\circ e_2=e_2\circ e_1=\lambda e_2$ ， $\left(A,\circ \right)$ 同构于A²型的预李代数；

(3) $e_1\circ e_1=\mu e_2,e_1\circ e_2=e_2\circ e_1=e_2\circ e_2=0$ ， $\left(A,\circ \right)$ 同构于A⁵型的预李代数；

(4) $e_1\circ e_1=\lambda e_1+\mu e_2,e_1\circ e_2=e_2\circ e_1=\lambda e_2$ ， $\left(A,\circ \right)$ 同构于A²型的预李代数。

证 由定理3，A上有基 $e_1,e_2$ 满足 $e_1\ast e_1=e_2$ ，且

$e_1\circ e_1=\lambda e_1+\mu e_2\text{,}{e}_1\circ e_2=e_2\circ e_1=\lambda e_2,\forall \lambda ,\mu \in ℂ$ .

根据二维左对称代数的分类，当 $\lambda =0,\mu =0$ 时，即

$e_1\circ e_1=e_1\circ e_2=e_2\circ e_1=e_2\circ e_2=0$ ,

此时 $\left(A,\circ \right)$ 同构于A⁴型的预李代数。

当 $\lambda \ne 0,\mu =0$ 时，即

$e_1\circ e_1=\lambda e_1,e_1\circ e_2=e_2\circ e_1=\lambda e_2$ ,

作非退化线性替换， $e_1{}^{\prime }=\frac{1}{\lambda }{e}_1$ ， $e_2{}^{\prime }=\frac{1}{{\lambda }^2}{e}_2$ ，有

$e_1{}^{\prime }\circ e_1{}^{\prime }=\frac{1}{\lambda }{e}_1\circ \frac{1}{\lambda }{e}_1=\frac{1}{\lambda }{e}_1=e_1{}^{\prime }$ ,

$e_1{}^{\prime }\circ e_2{}^{\prime }=\frac{1}{\lambda }{e}_1\circ \frac{1}{{\lambda }^2}{e}_2=\frac{1}{{\lambda }^2}{e}_2=e_2{}^{\prime }$ ,

$e_2{}^{\prime }\circ e_1{}^{\prime }=\frac{1}{{\lambda }^2}{e}_2\circ \frac{1}{\lambda }{e}_1=\frac{1}{{\lambda }^2}{e}_2=e_2{}^{\prime }$ .

此时 $\left(A,\circ \right)$ 同构于A²型的预李代数。

当 $\lambda =0,\mu \ne 0$ 时，即

$e_1\circ e_1=\mu e_2,e_1\circ e_2=e_2\circ e_1=e_2\circ e_2=0$ ,

作非退化线性替换， $e_1{}^{\prime }=\frac{1}{\mu }{e}_1$ ， $e_2{}^{\prime }=\frac{1}{\mu }{e}_2$ ，有

$e_1{}^{\prime }\circ e_1{}^{\prime }=\frac{1}{\mu }{e}_1\circ \frac{1}{\mu }{e}_1=\frac{1}{\mu }{e}_2=e_2{}^{\prime }$ ,

$e_1{}^{\prime }\circ e_2{}^{\prime }=e_2{}^{\prime }\circ e_1{}^{\prime }=e_2{}^{\prime }\circ e_2{}^{\prime }=0$ .

此时 $\left(A,\circ \right)$ 同构于A⁵型的预李代数。

当 $\lambda \ne 0,\mu \ne 0$ 时，即

$e_1\circ e_1=\lambda e_1+\mu e_2,e_1\circ e_2=e_2\circ e_1=\lambda e_2$ ,

作非退化线性替换，令 $e_1{}^{\prime }=\frac{1}{\lambda }{e}_1-\frac{\mu }{{\lambda }^2}{e}_2$ ， $e_2{}^{\prime }=e_2$ ，有

$e_1{}^{\prime }\circ e_1{}^{\prime }=\frac{1}{{\lambda }^2}{e}_1\circ e_1-\frac{2\mu }{{\lambda }^3}{e}_1\circ e_2=\frac{1}{{\lambda }^2}\left(\lambda e_1+\mu e_2\right)-\frac{2\mu }{{\lambda }^3}{e}_2=\frac{1}{\lambda }{e}_1-\frac{\mu }{{\lambda }^2}{e}_2=e_1{}^{\prime }$ ,

$e_1{}^{\prime }\circ e_2{}^{\prime }=\left(\frac{1}{\lambda }{e}_1-\frac{\mu }{{\lambda }^2}{e}_2\right)\circ e_2=\frac{1}{\lambda }{e}_1\circ e_1=e_2=e_2{}^{\prime }$ ,

$e_2{}^{\prime }\circ e_1{}^{\prime }=e_2\circ \left(\frac{1}{\lambda }{e}_1-\frac{\mu }{{\lambda }^2}{e}_2\right)=\frac{1}{\lambda }{e}_1\circ e_1=e_2=e_2{}^{\prime }$ .

此时 $\left(A,\circ \right)$ 同构于A²型的预李代数。

5. 二维预泊松代数在同构意义下的分类

定理5 设 $\left(A,\ast ,\circ \right)$ 是二维预泊松代数， $e_1,e_2$ 为A的基，则二维预泊松代数在同构意义下有以下三类：

(1) $e_1\ast e_1=e_2;e_1\circ e_1=e_1\circ e_2=e_2\circ e_1=e_2\circ e_2=0$ 。

(2) $e_1\ast e_1=e_2;e_1\circ e_1=\lambda e_1,e_1\circ e_2=e_2\circ e_1=\lambda e_2,e_2\circ e_2=0$ 。

(3) $e_1\ast e_1=e_2;e_1\circ e_1=\mu e_2,e_1\circ e_2=e_2\circ e_1=e_2\circ e_2=0$ 。

其中。

证 由定理4，设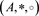是二维预泊松代数，取 $e_1,e_2$ 为A的一组基，使 $e_1\ast e_1=e_2$ ，此时， $\left(A,\circ \right)$ 同构于A⁴型、A²型、A⁵型、A²型的预李代数。

由于在A上A⁴型、A²型、A⁵型对应的预李代数类型不同，因此定理4中的第(1)，(2)，(3)种类型不同构，从而只需要计算定理4中的第(2)种和第(4)种是否同构即可。

设 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 是定理4中的第(2)种预泊松代数， $\left(A_2,{\ast }_2,{\circ }_2\right)$ 是定理4中的第(4)种预泊松代。取 $e_1,e_2$ 为满足定理4中第(2)种预泊松代数的 $A_1$ 的一组基， $e_1{}^{\prime },e_2{}^{\prime }$ 为满足定理4中第(4)种预泊松代数 $A_2$ 的一组基。下面找可逆线性变换 $f:A_1\to A_2$ ，满足

$f\left(e_i{\ast }_1{e}_j\right)=f\left(e_i\right){\ast }_{2}f\left(e_j\right),f\left(e_i{\circ }_1{e}_j\right)=f\left(e_i\right){\circ }_{2}f\left(e_j\right),\forall i,j=1,2.$

即f使 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 与 $\left(A_2,{\ast }_2,{\circ }_2\right)$ 同构。

设线性变换f在基 $e_1,e_2$ 下的矩阵为 $F={\left(f_{ij}\right)}_{2\times 2}$ ，即

$f\left(e_1,e_2\right)=\left(e_1{}^{\prime },e_2{}^{\prime }\right)\left(\begin{array}{cc}{f}_{11}& f_{12}\\ f_{21}& f_{22}\end{array}\right),f_{ij}\in ℂ,i,j=1,2.$

一方面，f为Zinbiel代数的同构需要满足以下4个方程：

$f\left(e_1\ast e_1\right)=f\left(e_2\right)=f\left(e_1\right)\ast f\left(e_1\right)=\left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right)\ast \left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right)$ ,

$f\left(e_1\ast e_2\right)=0=f\left(e_1\right)\ast f\left(e_2\right)=\left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right)\ast \left(f_{12}{e}_1{}^{\prime }+f_{22}{e}_2{}^{\prime }\right)$ ,

$f\left(e_2\ast e_1\right)=0=f\left(e_2\right)\ast f\left(e_1\right)=\left(f_{12}{e}_1{}^{\prime }+f_{22}{e}_2{}^{\prime }\right)\ast \left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right)$ ,

$f\left(e_2\ast e_2\right)=0=f\left(e_2\right)\ast f\left(e_2\right)=\left(f_{12}{e}_1{}^{\prime }+f_{22}{e}_2{}^{\prime }\right)\ast \left(f_{12}{e}_1{}^{\prime }+f_{22}{e}_2{}^{\prime }\right)$ .

通过计算得

$f_{22}=f_{11}^2,f_{12}=0$ .

此时

$f\left(e_1,e_2\right)=\left(e_1{}^{\prime },e_2{}^{\prime }\right)\left(\begin{array}{cc}{f}_{11}& 0\\ f_{21}& f_{11}^2\end{array}\right)$ .

另一方面，f为预李代数的同构需要满足以下4个方程：

$f\left(e_1{\circ }_1{e}_1\right)=\lambda f\left(e_1\right)=f\left(e_1\right){\circ }_{2}f\left(e_1\right)=\left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right){\circ }_2\left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right)$ ,

$f\left(e_1{\circ }_1{e}_2\right)=\lambda f\left(e_2\right)=f\left(e_1\right){\circ }_{2}f\left(e_2\right)=\left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right){\circ }_2\left(f_{11}^2{e}_2{}^{\prime }\right)$ ,

$f\left(e_2{\circ }_1{e}_1\right)=\lambda f\left(e_2\right)=f\left(e_2\right){\circ }_{2}f\left(e_1\right)=\left(f_{11}^2{e}_2{}^{\prime }\right){\circ }_2\left(f_{11}{e}_1{}^{\prime }+f_{21}{e}_2{}^{\prime }\right)$ ,

$f\left(e_2{\circ }_1{e}_2\right)=0=f\left(e_2\right){\circ }_{2}f\left(e_2\right)=\left(f_{11}^2{e}_2{}^{\prime }\right){\circ }_2\left(f_{11}^2{e}_2{}^{\prime }\right)$ .

由于f为同构映射，则 $f_{11}\ne 0$ ，通过计算得

$f_{11}=\frac{\lambda }{\gamma },f_{21}=-\frac{\lambda \mu }{{\gamma }^2},f_{22}=\pm \frac{\lambda }{\gamma }$ .

综上，取 $f_{11}=\frac{\lambda }{\gamma },f_{21}=-\frac{\lambda \mu }{{\gamma }^2},f_{22}=\frac{\lambda }{\gamma }$ ，则

$\left|\begin{array}{cc}{f}_{11}& f_{12}\\ f_{21}& f_{22}\end{array}\right|=\left|\begin{array}{cc}{f}_{11}& 0\\ f_{21}& f_{11}^2\end{array}\right|=f_{11}^3=\frac{{\lambda }^3}{{\mu }^3}\ne 0$ .

因此，取

$F=\left(\begin{array}{cc}\frac{\lambda }{\gamma }& 0\\ -\frac{\lambda \mu }{{\gamma }^2}& \frac{\lambda }{\gamma }\end{array}\right)$ ,

f即为 $\left(A_1,{\ast }_1,{\circ }_1\right)$ 和 $\left(A_2,{\ast }_2,{\circ }_2\right)$ 的同构映射。因此，二维预泊松代数 $\left(A,\ast ,\circ \right)$ 在同构意义下有三类。

通过定理5，我们得到了二维我们得到了二维的预泊松代数在同构意义下的完全分类，为进一步考虑预泊松代数的分类、扩张以及预泊松代数上的特殊算子等问题提供了基础。

6. 总结与展望

本文通过计算二维预泊松代数上的预李代数的类型，得到二维预泊松代数的同构关系，从而确定了二维预泊松代数的分类。在此研究方法的基础上，以三维Zinbiel代数的分类为基础，可以计算出三维预泊松代数的同构关系以及分类，该研究结果对预泊松代数进一步研究提供了便捷的分类结果，具有深刻意义。