基于傅立叶变换法的子口径抛光去除函数修正特性分析

Analysis of the Correction Characteristics of Sub-Aperture Polishing Function Based on Fourier Transform

摘要: 光学元件的超精密子口径抛光过程中，仿真加工与实际加工过程不一致将导致收敛出现反复，多次迭代冗余加工反而降低元件表面精度与收敛效率。本文基于傅立叶变化法分析子口径抛光去除函数的修正特性，针对其修正能力提出基于算法的修正补偿，通过在“非线性系统”下建立去除函数的动态补偿仿真模型，使得仿真过程更加符合实际，提高了确定性抛光过程的准确有效性，为超高精度面形误差修正工艺提供了关键技术支撑。

Abstract: For optical ultra-precision sub-aperture polishing, the inconsistency between simulation and ac-tual processing will affect the convergence of surface error, and reduce the machining accuracy and efficiency. In this paper, it analyzed the correction feature of remove function. For the algo-rithm compensation, the dynamic compensation simulation model of the removal function is es-tablished under the “nonlinear system”, which makes the simulation process more accurate. The determination of the polishing process is improved by compensation, which provides the key technical support for ultrahigh precision surface error correction process.

1. 引言

自70年代初期W.J.Rupp等提出采用计算机控制光学表面成形技术(Computer Controlled Optical Surfacing, CCOS)进行小工具研磨实现光学镜面的加工，从而实现大口径光学元件高精度表面误差修正。随着CCOS技术的不断发展，计算机、精密测量、新工艺、新材料等综合技术不断完善，又相继衍生出大量相关技术例如：气囊抛光、射流抛光、大气等离子体抛光、磁流变抛光、离子束抛光等先进的确定性抛光技术，基本满足了超高精度光学制造领域针对激光损坏阈值、亚表面损伤等高要求。

基于CCOS技术实现光学元件表面误差收敛的工作原理即将去除函数提取出来，根据定量的面形检测数据和抛光加工过程的控制模型，在工艺软件的控制下，以一定的路径、速度和压力抛光工件表面，通过控制抛光头在光学元件表面的驻留时间，精确控制元件表面材料的去除量，从而改善元件的局部面形误差，达到最终的面形精度要求，因此掌握该抛光技术的核心问题之一即去除函数的误差修整能力并有效补偿。传统仿真加工过程在“线性移不变系统”模式下，采用静态固定的去除函数，与实际加工过程去除函数在时间域与空间域上会不断变化的动态特性不一致。使其与实际加工更加吻合。本文通过分析去除函数的修正特性，通过补偿来修正仿真与实际过程的去除函数不一致，使仿真过程更加贴近实际，极大提高超精密加工的确定性及有效性。

2. 去除算法基本原理

在CCOS技术中，去除算法需要对硬件设施的出口数据提供录入接口，获取光学元件的面形情况及机床驱动设备的运动参数设置，经核心算法的分析处理，确定磨头的抛光路径及驻留函数，同时选择合适的加工参数，通过控制磁流变抛光头在工件表面的驻留时间，准确控制工件表面的定点、定量去除，进入模拟加工模块，预期模拟加工后的面形结果，最终由操作人员判断收敛是否有效，并生成机控程序指导实际加工，达到预期的材料去除量，实现光学元件面形的快速收敛，至此，一个加工周期结束。如此循环，实现“单次测量，多工序生成”的加工模式，根据Preston光学表面成形模型假设 [1] [2] ，如式(1)。

$\Delta Z\left(x,y\right)=kP\left(x,y\right)V\left(x,y\right)$ (1)

假设工具的去除函数是当工件不动的情况下，一个运动周期中单位时间内，在工件与工具相互作用区域内各点材料平均去效率的分布函数用R(x,y)表示，如式(2)：

$R\left(x,y\right)=\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}\Delta Z\left(x,y\right)\text{d}t}=\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}kP\left(x,y\right)V\left(x,y\right)\text{d}t}$ (2)

式中：T——加工周期；

ΔZ(x, y)——磨头与工件接触区域中某点单位时间内的材料去除量；

P(x, y)——磨头与工件在对应点处的相对压力；

V(x, y)——磨头与工件在对应点处的相对运动速度；

k——与加工过程有关的比例常数。

3. 基于傅里叶变换法的去除函数形貌分析

常用求解驻留时间的算法有按比例估算法、傅立叶变换法以及简森–范锡图特法等 [3] 。本文采用傅里叶变换法分析几种形态的去除函数形貌。通过分析卷积加工过程可知，在同速轨迹段内某一点的加工量，就是去除函数在轨迹方向的积分与驻留时间的乘积 [4] 。假定轨迹方向为x方向，则可以计算出去除函数的实际作用积分量在y方向上的归一化去除函数积分分布函数R_n(y)，计算公式如式(3)。式中y表示y方向覆盖范围[−r, r]，r表示为y方向去除函数抛光区域半径。

$R_n\left(y\right)=\frac{R\left(y\right)}{\max \left(R\left(y\right)\right)}=\frac{{\displaystyle \underset{0}{\overset{T}{\int }}\Delta Z\left(y\right)\text{d}t}}{\max \left({\displaystyle \underset{0}{\overset{T}{\int }}\Delta Z\left(y\right)\text{d}t}\right)}$ (3)

如图1(a)所示为任意相貌的去除函数三维空间去除量分布，进行轨迹方向的积分处理得到去除函数分布图1(b)，取x方向去除函数积分在y方向上分布最大的值，得到x方向的总积分二维分布图1(c)。其中图1(c)为积分公式(3)所示去除函数的实际作用积分量在y方向上的分布函数R_n(y)。因此去除函数修正能力截止频率的分析也可以等效在二维分布函数上R_n(y)来分析。

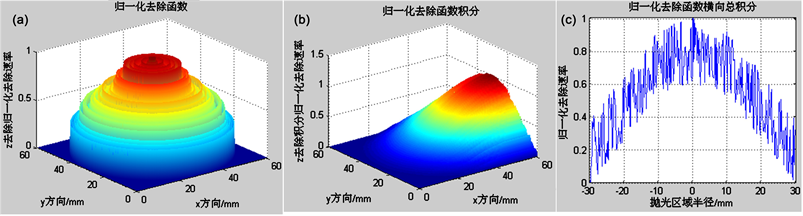(a) 三维空间去除量分布；(b) x方向去除积分分布；(c) x方向总积分

Figure 1. Normalized removal function

图1. 归一化去除函数

对式(3)进行傅里叶变换，得到R_n(y)的频谱，如式(4)。

$R_F\left(\omega \right)={\displaystyle \underset{-r}{\overset{r}{\int }}{R}_n\left(y\right){\text{e}}^{-i\omega y}}\text{d}y$ (4)

去除函数的截止频率是根据去除函数的幅值频谱 $\left|R_F\left(\omega \right)\right|$ 确定的。为便于比较各去除函数的修形能力，

本文选择幅值谱线下降到峰值的5%处对应的频率为去除函数的截止频率，将从去除函数形貌这个角度来分析去除函数的误差修正能力 [5] 。将去除函数的形貌分为高斯型、三角形、梯形、脉冲随机震荡型形状，分析在同等去除尺寸，即去除区域大小相同(r = 30 mm)的条件下各种形貌去除函数误差修正能力。

4. 高斯型去除函数截止修正能力分析

高斯型去除函数分布如式(5)所示：

$R\left(x,y\right)=\frac{1}{\sqrt{2\text{π}}\sigma }{\text{e}}^{-\frac{x^2+y^2}{2{\sigma }^2}}$ (5)

取σ = r/3，即取正态分布的3σ原则，进行模拟分析，所得到的三维去除分布图2(a)、三维去除积分分布图2(b)、x方向总积分分布图2(c)，以及归一化幅值频谱图如图2(d)。仿真结果表明，此参数条件下的截止频率为0.04383 mm⁻¹，即该去除函数误差修正能力为可修正大于22.81 mm空间周期的误差。

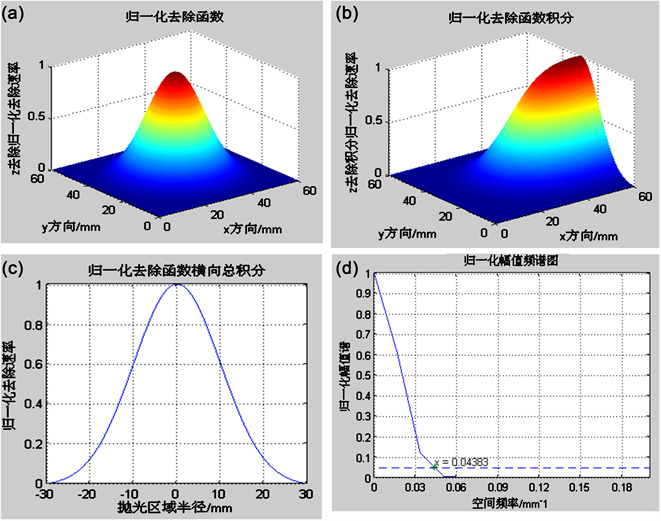(a) 三维空间去除量分布；(b) x方向去除积分分布；(c) x方向总积分；(d) 归一化幅值频谱图

Figure 2. Normalized Gaussian removal function

图2. 归一化高斯型去除函数

σ为去除函数的形状调节参数，有效去除占比(在去除函数区域内有效去除的体积与矩形区域体积之比)与σ参数密切相关，是高斯型去除函数的主要调制参数，图3所示为σ去除函数截止修正能力的关系图。

(a) σ值与截止修正频率；(b) σ值与截止修正误差；(c) σ值与有效去除比例；(d) 有效修正占比与截止频率

Figure 3. Relationship between σ and Gaussian shape removal function correction ability

图3. σ与高斯形去除函数修正能力的关系

由分析结果上可以看出：

1) 图3(a)表明，随着σ增大，其截止修正频谱值越来越小，在σ = 15 mm之后开始增大，之后再σ = 60 mm之后基本平缓，截止修正频谱在0.037 mm⁻¹附近。

2) 图3(b)表明，随着σ增大，截止修正误差尺度越来越大，在σ = 15 mm之后开始下降，之后再σ = 60 mm之后基本平缓，截止修正误差尺度位置在[1.4 mm, 31.5 mm]附近。

3) 图3(c)表明，随着σ增大，其有效去除占比越来越大，也就去除所覆盖的区域更多。

4) 图3(d)表明，随着有效去除占比的增大，截止修正频率也逐渐降低，即所能够修正的误差尺度范围变小。

由高斯型去除函数的修正能力分析可知，选取了影响其修正能力的最大等效二维去除积分总和，所有的截止修正能力的分析也是基于此分布曲线来分析，因此后面所有形貌的去除函数分析，也均是对积分后的形貌进行频域以及空域内的修正能力进行分析。

5. 基于算法的修正补偿

5.1. 算法修正补偿原理

由于模拟加工仅考虑理想情况下的静态去除函数与被加工元件原始面形之间的卷积运算 [4] 。传统的CCOS抛光面形修正算法设计中，假定去除函数在整个抛光过程中不发生改变。

假设τ(x, y)为工具的驻留时间函数，它表示磨头在点s(x, y)处的驻留时间。工具在工件表面以不同的速度移动时，工件表面材料去除量的分布函数e(x, y)与τ(x, y)，r(x, y)的关系如下：在轨迹path上s(x, y)点处的去除量e(x, y)。对于去除函数来说r(x, y)会因为移动而产生坐标系的变化，因此需要在每一个去除函数r(ξ,η)通过轨迹上所有点各自分别停留τ(x, y)时间对s(x, y)的去除量e(s_i, x, y)之和如式(6)：

$\{\begin{array}{l}e\left(x,y\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}e\left(s_i,x,y\right)}\\ e\left(s_i,x,y\right)=r\left(\xi ,\eta \right)\Delta \xi \Delta \eta \tau \left(x-\xi ,y-\eta \right)\end{array}$ (6)

由式(6)可写成积分形式为：

$e\left(x,y\right)={\displaystyle \underset{path}{\iint }r\left(\xi ,\eta \right)\tau \left(x-\xi ,y-\eta \right)\text{d}\xi \text{d}\eta }=r\left(x,y\right)\otimes \tau \left(x,y\right)$ (7)

由式(7)采用傅里叶变换及逆变换可得式(8)，即为常见的静态模型求解驻留时间的方程式：

$\tau \left(x,y\right)=F^{-1}\left[E_f\left({\omega }_x,{\omega }_y\right)/R_f\left({\omega }_x,{\omega }_y\right)\right]$ (8)

式中：

$E_f\left({\omega }_x,{\omega }_y\right)$ ——e(x,y)傅里叶变换函数；

$R_f\left({\omega }_x,{\omega }_y\right)$ ——r(x,y)傅里叶变换函数。

去除函数是一直都在发生变化，由此导致仿真加工面形与实际加工面形存在差异，面形收敛缓慢甚至出现反复。式(8)为常见的基于“线性移不变系统”求解驻留时间的方程式，传统静态算法模型，采用的“线性不变系统”假设与实际加工过程的非线性变化系统不相符。本课题需要讨论的是去除函数r(x, y)在加工过程中是一个不断变换的变量，因此，采用直接采用式(8)来设计算法求解驻留时间矩阵显然不合适，需要在此基础上，根据去除函数的动态特性进行性修正，使得模拟加工过程更能够反映真实情况。

通过参数补偿可以在一定程度上补偿的去除速率的变化，但是在补偿后依然存在无法反应去除函数变化不均等的问题。为弥补每一点分布磨损量不同的问题，可以设计动态补偿算法，在加工仿真过程中进行充分考虑，从而提高仿真的符合度，以及实际加工的确定性。

5.2. 基于时间轴磨损补偿算法

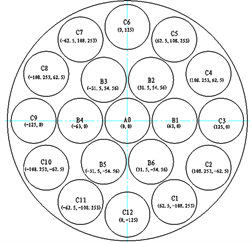(a)位置分布 (b)去除函数形貌

Figure 4. Time-based removal of spots

图4. 基于时间轴的去除斑制作

工程实际过程不能采集或存储到每一个时刻的实际去除函数信息，需要基于一定精度的离散数据进行拟合来获得任意时刻的去除信息。以小工具数控抛光磨损曲线采集为例，按照稳定性控制措施行严格控制的条件下，在Φ320 mm ´ 40 mm熔石英元件上不同位置(分为A、B、C三个区域共19个点，如图4(a)，分别定点抛光4 min，共76 min，基本涵盖了一般情况下单次修磨抛光模以及更换抛光粉的时间范围。在抛光模以及抛光液使用不同时间状态下获得各个时间节点的去除函数，如图4(b)，模拟了抛光过程去除函数随时间的变化。以去除函数的体积去除速率作为考察对象，计算出图4(a)中每一位置去除函数的体积去除速率，并绘制出其变化曲线，可以获得去除函数的体去除速率在时间轴上的变化趋势如图5所示。

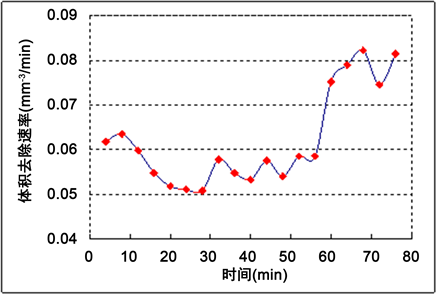
Figure 5. Gadget NC removal function volume removal rate wear curve

图5. 小工具数控去除函数体积去除速率磨损曲线

此外，还可以获得去除函数所对应每一个位置的动态去除速率与起始去除速率相比的去除变化率曲线，即 $f\left(x,y,t\right)t\in \left[0,T\right]$ ，其中T为单次抛光时间。由于采集时间轴上的去除函数不可能是连续的点，一

般都是离散的数据点。因此，可以通过拟合的方式获得任意一时间点上的去除信息。可以采用NURBS样条拟合的方式获得一条光顺的去除速率变化曲线。

$f\left(x,y,t\right)=\frac{NURBS\left(R\left(x,y,t_1\right),R\left(x,y,t_2\right),\cdots ,R\left(x,y,t_n\right),t\right)}{R\left(x,y,t_1\right)}$ (9)

其中，在任意离散点t_i时刻的去除函数 $R\left(x,y,t_i\right)$ ，可以通过多次(可令为：m次)实验取平均的方式进行优化获得如式(10)。

$R\left(x,y,t_i\right)=\frac{1}{m}{\displaystyle \underset{j=1}{\overset{j=m}{\sum }}{R}_j\left(x,y,t_i\right)}$ (10)

获得基于第一个去除函数的去除速率变化曲线函数 $f\left(x,y,t\right)$ 后，就可以将第一个去除函数作为输入参数，建立任意时间点上的去除函数 $R\left(x,y,t\right)$ [6] ，其表达式为：

$R\left(x,y,t\right)=f\left(x,y,t\right)\times R\left(x,y,t_1\right)$ (11)

式(11)即为所需要建立的补偿算法模型。由于加工某一点是在去除函数有效范围内所有驻留点叠加的一种综合效果，假定在所有能够加工到该点范围内的时间是比较短，可忽略该段时间内去除函数所产生的变化。由于上文所建立的补偿模型主要是时间相关模型，因此可以将驻留时间τ(x, y)做一定的修改变为τ(x,y,t)。

$\tau \left(x,y,t\right)=F^{-1}\left[\frac{E_f\left({\omega }_x,{\omega }_y\right)}{R_f\left({\omega }_x,{\omega }_y,t\right)}\right]=F^{-1}\left[\frac{E_f\left({\omega }_x,{\omega }_y\right)}{f_f\left({\omega }_x,{\omega }_y,t\right)\times R_f\left({\omega }_x,{\omega }_y,t_1\right)}\right]$ (12)

式(12)即为基于补偿模型修正过的驻留时间求解方程式，任意一点被加工时抛光模已经工作时间为t。算法具体实现过程如下：

1) 输入材料离散的去除函数矩阵 $R\left(t_1,t_2,\cdots ,t_n\right)$ ，并拟合得到连续的动态去除函数 $R\left(x,y,t\right)$ ；

2) 输入原始误差矩阵 $E_0\left(x,y\right)$ ，计算材料去除量矩阵 $E\left(x,y\right)$ ；

3) 设定初始值i = 1，共均匀分布M × N个驻留时间点；

4)采用式(10)计算第i个驻留点 $p\left(x_i,y_i,t_i\right)$ 处的驻留时间 $\tau \left(x_i,y_i,t_i\right)$ ，此时刻为t_i， $t_i={\displaystyle \underset{k=1}{\overset{i-1}{\sum }}{t}_k}+\tau \left(x_i,y_i,t_i\right)$ ，

5) 判断i值，若 $i\ge M\times N$ ，则转入第(f)步，否则 $i=i+\text{1}$ 转入第(d)不继续计算；

6) 计算残余误差矩阵 $E_r\left(x,y\right)=E\left(x,y\right)-\left[R\left(x,y,t\right)\times {\eta }_v\left(x,y\right)\right]\otimes \tau \left(x,y,t\right)$ ，其中 ${\eta }_v\left(x,y\right)$ 为动态运动去除函数补偿因子，即动态去除与定点抛光的去除速率差异因子 ${\eta }_v\left(x,y\right)=R_v\left(\sqrt{x^2+y^2}\right)/R_s\left(\sqrt{x^2+y^2}\right)$ ，速度为 $\stackrel{•}{l}/\tau \left(x\text{,}y,t\right)$ ，其中 $\stackrel{•}{l}$ 为单位间隔进给向量；

7) 计算剩余误差矩阵即： $E_s\left(x,y\right)=E_0\left(x,y\right)-E_r\left(x,y\right)$ ，此误差矩阵即为模拟加工残余误差矩阵结果。

5.3. 修正算法模拟结果分析

根据工艺软件对去除函数进行基于算法的修正补偿模拟加工如图6所示，实际加工得出的面形如图7所示，从图中可以得出结论：工艺软件中对去除函数进行基于算法的修正补偿模拟加工与实际加工元件的面形分布趋势一致，预期面形与实际加工面形结果基本吻合，充分证明该补偿算法用于控制光学表面加工的准确性、有效性。

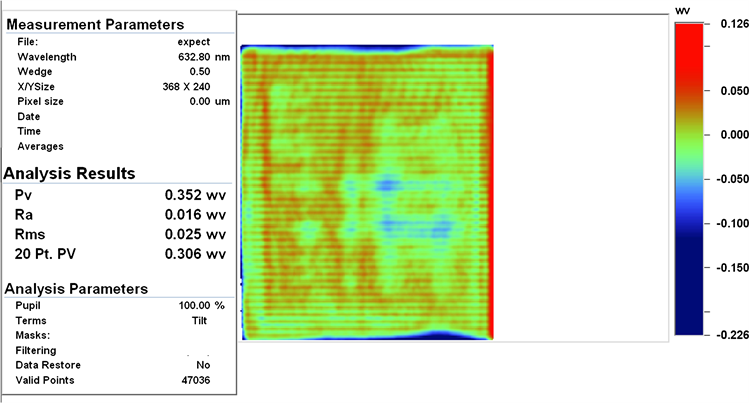
Figure 6. Process software simulation processing results

图6. 工艺软件模拟加工结果图

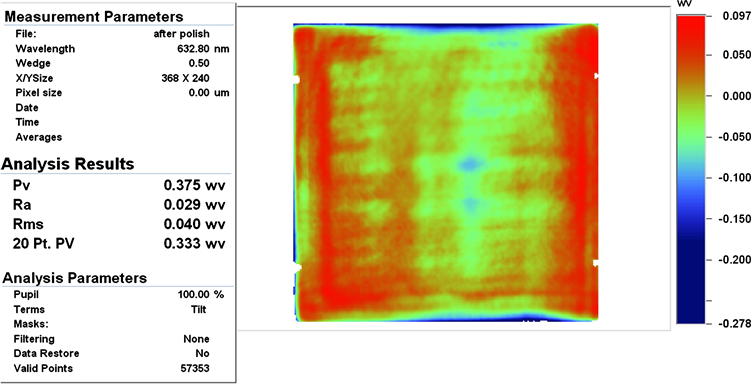
Figure 7. Actual processing back shape distribution

图7. 实际加工后面形形貌分布

6. 结论

仿真加工与实际加工过程不一致将导致收敛出现反复，并降低加工精度与效率。传统仿真加工过程在“线性移不变系统”模式下，采用的是静态固定的去除函数 [7] 。这与实际过程去除函数在时间域与空间域上的不断变化的动态特性不一致。仿真与实际过程的去除函数不一致可以通过补偿来修正，使得两者更接近，从而提高加工的确定性。本课题将补偿方法分为基于工艺参数的补偿与基于算法的修正补偿。对于工艺参数的补偿，通过不断调整具有实时响应特性的参数调制实际加工过程的去除函数，以弥补去除速率的非线性变化。对于算法的修正补偿，通过在“非线性系统”下建立去除函数的动态补偿仿真模型，使得仿真过程更加符合实际。提高了抛光过程的确定性，为超高精度面形误差修正工艺提供了关键技术支撑。

NOTES

^*通讯作者。