1. 引言
热传导方程是一类重要的拋物型偏微分方程。其一维形式如下
其中t是时间变量,x是空间变量,
表示t时刻在位置x处的温度,
为常数,它取决于材料的热传导率、密度和热容,
为给定的函数,表示热源。作为模型方程,除了描述一个区域内温度如何随时间变化以外,热传导方程常也被应用于金融、自然环境、工程设备及生物机体某些物理现象的研究中 [1] 。由于其精确解往往不容易求得 [2] ,因此研究其数值求解方法无疑具有非常重要的理论意义和工程应用价值。
由现有文献知,热传导方程的数值求解方法主要有有限差分法、有限元法、谱方法等 [3] [4] [5] [6] ,其中应用最广泛的是差分法和边界元方法。差分法在求解问题时要求对整个区域作网格剖分,所以对复杂区域生成质量较好的网格非常耗时,特别是边界不规则时计算精度也不高。边界元方法要作复杂的奇异积分,费时费力。传统方法在一定程度上给出了满足精度要求的数值解,但它们都是网格方法,求解过程依赖于区域的网格剖分,本文考虑使用真正无网格方法数值求解热传导方程,希望能达到计算精度高,计算量小,使用方便,适应性强等好的效果。
2. 热传导方程的径向基无网格线方法
径向基线方法 [7] 是一种不依赖网格剖分的真正无网格方法。其基本思想是首先在离散点上运用径向基函数来近似空间导数,将偏微分方程问题转化为的常微分方程组问题,再利用常微分方程组的高精度数值方法进行求解,最终得到偏微分方程的高精度数值解。
下面考虑热传导方程的初边值问题
(1)
(2)
(3)
其中已知函数
表示初始温度分布情况,已知函数
,
表示区间
两个端点处温度随时间的变化情况。
首先,将求解区间进行离散,得到N个离散节点
,其中
是内部点,而
和
是边界点,借助径向基函数得到方程解得近似函数,用
表示为
(4)
其中
是与时间相关的未知量。
令
(5)
引入向量符号
,
(6)
其中
(7)
(8)
则
(9)
由(5)和(6)可以得到
(10)
其中
(11)
将(10)代入(1),按照顺序将
代入得到
(12)
其中
(13)
(14)
(15)
为了把上面的系统写成列向量的形式,令
(16)
(17)
则(12)可改写为
(18)
令
(19)
则
(20)
初始条件为
(21)
又由(2)式给出边界条件
(22)
通过上述方法可将热传导方程问题转化为常微分方程组问题,可以借助如下Runge-Kutta方法进行求解。
(23)
其中
是时间步长.在Runge-Kutta方法中,只要时间步长
足够小,就能保证求解的稳定性 [2] 。
3. 数值实验
我们考虑热传导方程的初边值问题(1)~(3),该问题的真解是
.
为衡量数值解的精度,定义误差如下:
其中
和
分别是真解和数值解。
为了考察基于径向基函数的无网格线方法在热传导方程数值求解中的可行性和有效性,我们下面分别讨论T时刻的数值解情况(图像、误差)以及不同参数对数值解的影响情况。
首先,给出时刻T = 1,33个离散节点时数值解(图1)及其误差(图2)图像。

Figure 1. Comparison of exact and numerical solutions
图1. 真解数值解对比图
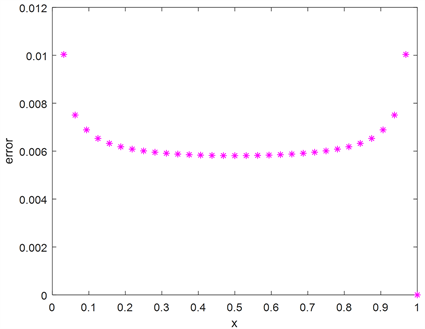
Figure 2. The distribution of maximum relative error
图2. 误差分布图
由图1可得,计算所得数值解与真解贴合程度较好,说明所求数值解精确度较高,能一定程度上满足人们对热传导方程解的需求。分析图2可知,数值解的最大相对误差在区间的两个端点处最大,在区间内部,误差较小且变化幅度不大,说明数值解在区间内部可以达到更高的精确。
其次,我们固定所有参数,考虑不同时刻的数值解的图像(图3)和最大相对误差(表1)情况。
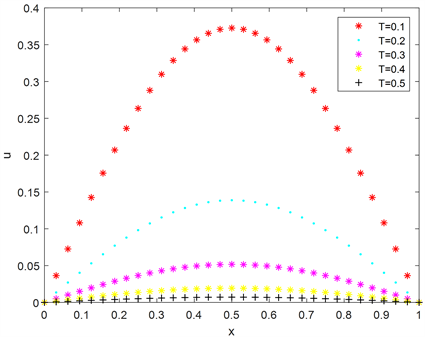
Figure 3. Numerical solutions at different times
图3. 不同时刻的数值解图像
通过观察图3可以知道,数值解完美反映了不同时刻解曲线的特征:在区间
上的变化趋势为先增大后减小,关于
对称,随着考虑时刻T的增大,曲线趋于平缓,弯曲程度逐渐减小。
表1的数据说明,当时刻T逐渐增大时,数值解的误差随之增大。但当时刻T小于1时,误差小于0.01,此时具有较高的精度。
最后,讨论比例系数和离散节点数目对数值解精度的影响情况。比例系数RAT定义为
其中
是时间步长,h是等分节点的间距。

Table 1. Maximum relative errors at different times
表1. 不同时刻的误差情况
通过多次数值实验,我们发现RAT对数值解的稳定性和精度有较大影响,并当其超过某一定值时,数值解的稳定性无法保证,误差也随之骤然上升(如图4)。

Figure 4. The changing errors with proportional coefficient RAT
图4. 误差随比例系数RAT的变化
分析实验结果可得,RAT突变点在0.3附近取得,约为0.2818。故当T = 0.5时,RAT在
范围内变动时误差较小,数值解结果较精确。
表2列出了固定比例系数RAT的值为0.02,时间T的值为1,进行数值实验后得到的最大相对误差随节点数目的变化情况。由表2可知,当N以10为步长增加时,数值解误差随之减小,并当N = 31时误差小于0.01,达到较精确的程度。
4. 结论
文章借助径向基函数无网格线方法数值求解一维热传导方程的初边值问题,在空间上使用径向基函

Table 2. Maximum relative errors with different nodes
表2. 不同离散节点对应的误差
数进行逼近,将偏微分方程问题转化为常微分方程组问题,进而利用Runge-Kutta方法得到高精度数值解。数值实验表明径向基无网格方法步骤简洁、易于操作,实验结果说明了该方法的可行性和有效性。因此,有必要进一步推广和完善该方法。
基金项目
大学生创新创业训练计划项目(201810452015),山东省自然科学基金项目(ZR2018LA008)。
NOTES
*通讯作者。