1. 引言
在统计学的教材 [1] [2] 或者时间序列教材 [3] 中提到,如果现象的长期趋势随着时间的推移按照线性变化,则可以对时间序列拟合趋势直线。如果现象的趋势随着时间的推移出现非线性趋势,则需要配合适当的趋势曲线。趋势曲线的形式又很多,有抛物线型、指数曲线型、修正指数曲线型、龚珀茨曲线型、逻辑斯蒂曲线型等。当现象的变化形态不是按照某种固定的形态变化,而是有升有降,在变化过程中可能有几个拐点。这时就需要拟合k阶趋势曲线,即多项式函数。当只有一个拐点时,可以拟合二阶曲线,即抛物线。当有两个拐点时,需要拟合三阶曲线。当有k − 1个拐点时,需要拟合k阶曲线。
段树乔和段方婕 [4] 提出了带有电源供给能力约束条件的回归函数筛选及其综合方法,并建立了电网公司售电量的多项式回归预测模型及其检验方法,并通过一个具体实例详细说明了该方法的应用。温鲜等人 [5] 以柳州市房地产价格为例,建立了柳州市房地产价格的多项式回归模型,并进行实证分析、检验模型精度,并预测了未来三年柳州市的房地产价格。于媂和姜潮 [6] 采用多项式回归模型和灰色预测模型对辽宁省省医院药品比例进行分析预测。徐颖和黄素珍 [7] 利用百度搜索数据,以江苏省南京市为例建立了新建住宅销售价格指数的多元线性回归、完全二次多项式回归和逐步回归模型。张磊等人 [8] 将灰色多项式回归组合模型应用在维修器材需求方面。在模型中,作者利用最小二乘法得到了灰色多项式组合预测模型的各项系数,并分别运用灰色二项式、三项式、四项式回归组合模型对数据进行建模分析。计算结果表面,灰色多项式回归组合模型可以大幅度提高数据的拟合精度,并且随着拟合项数的增加,拟合精度逐渐提高。
从上面的研究文献中可以看出,确定模型系数的方法基本上采用的都是最小二乘法。它通过最小化误差的平方和寻找数据的最佳函数匹配,使得计算得到的数据与实际数据之间的误差的平方和最小。但是,在求解修正的指数曲线的系数时,教材并没有使用最小二乘法,而是采用的分段求和的思想,即三和法求解模型中参数的具体表达式。受到此模型参数求解思路的启发,我们将分段求和的思想引入到k阶趋势曲线的参数求解中,得到了模型系数的表达式。最后,以教材中的两个具体实例,进一步分析了该方法的可行性和有效性。
本文的结构安排如下:第2节给出三和法的具体计算过程,以便引入到k阶趋势曲线中。第3节讨论了分段求和方法在k阶趋势曲线模型参数的具体求解。第4节给出了两个具体的实例,以说明该方法的可行性和有效性。第5节给出了本文的结论。
2. 修正的指数曲线
由文献 [1] [2] [3] 可知,如果现象的趋势为:初期增长迅速,随后增长率逐渐减低,最终以一个常数为增长极限,则可以采用修正的指数曲线进行拟合。在经典指数曲线的基础上增加一个常数k,即得到修正指数曲线的方程,
, (1)
其中,a、b、k为未知参数,
,
,
。
参数a、b、k估计的基本思想是三和法:把整个时间序列分成相等的三个数组,每个组有m项,根据趋势值Yt的三个局部总和分别等于原数列观察值Yt的三个局部总和来确定三个参数。具体为:设观察值的三个局部总和分别为S1、S2、S3,得
,
,
。 (2)
由三和法得到如下方程
。 (3)
通过对方程(3)求解,得到
。 (4)
3. K阶趋势曲线
由文献 [1] 的13章可知,k阶趋势曲线函数的一般形式为
, (5)
其中
。教材中提到参数
可以按照多元回归分析中的最小二乘法具体求得,有兴趣读者可以参看相关资料。这里我们采用分段求和的思想给出参数
的具体表达式。
分段求和的思想是:把整个用于建模的时间序列分成相等的
个数组,每个组有m项,即用于建模的数据量为
。根据趋势值Yt的
个局部总和分别等于原序列观察值Yt的
个局部总和来确定参数
。具体为:设观察值的
个局部总和分别为
,得
。 (6)
于是,得到如下方程
。 (7)
在表达式(7)的计算中,我们要对形如
的表达式进行求解。很显然给出它的一般形式是很困
难的,有兴趣的可以去看Faulhaber数或者Harmonic数关于如何求解的问题。将表达式(7)写出矩阵的形式为:
(8)
通过求解矩阵方程(8),即可得到参数
的值,然后代入k阶曲线方程即可对数据进行拟合、预测。
当
时,求解线性趋势曲线
参数的表达式。首先,有
(9)
通过对方程(9)的求解得到,
(10)
当
时,求解线性趋势曲线
参数的表达式。首先,有
(11)
通过对方程(11)的求解得到,
,
,
。
4. 数值验证
首先,我们给出衡量模型精度的表达式,根据计算值与实际值确定绝对百分误差(APE)和平均绝对百分误差(MAPE)如下。
, (12)
, (13)
在表达式(13)中,当
,MAPE为拟合误差,记为
;当
,MAPE为预测误差,记为
;当
,MAPE为总误差,记为
,表达式中Yt为计算得到的值,
为用于建模的个数,n为原始序列的总个数。
例1:本例中的数据来源于文献 [2] 第167页表6~7的数据,作者在书中利用Excel分析工具对2005年至2015年我国国内生产总值数据建立了线性回归模型。作者们给出的线性回归方程的表达式为
。 (14)
在本文中,我们对上述数据采用我们提出的方法也进行了研究,其中建模的数据
,经过计算得到方程的表达式为
。 (15)
计算得到的相关数据见表1和图1。从表1可以看出,我们的结果与作者的结果非常的接近,其中书上的建模误差,拟合误差和预测误差分别为2.4021%,1.6818%和2.3300%。我们的建模误差,拟合误差和预测误差分别为1.8471%,3.1738%和1.9798%。

Table 1. The application of linear trend curve in China’s GDP
表1. 线性趋势曲线在我国国内生产总值中的应用
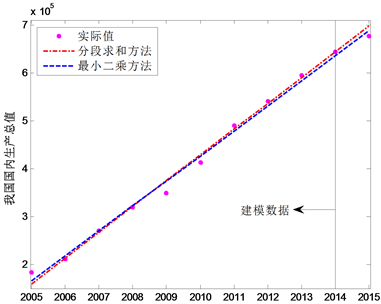
Figure 1. The linear trends of the China’s GDP
图1. 国内生产总值线性趋势图
例2:本例中的数据来源于文献 [1] 第345页例13.11的数据,作者在书中利用Excel分析工具对1990年至2009年金属切削机床产量建立了四阶趋势曲线模型。作者们给出的四阶趋势曲线方程的表达式为:
。 (16)
在本文中,我们对上述数据采用我们提出的方法也进行了研究,其中建模的数据
,经过计算得到方程的表达式为
。(17)
计算得到的相关数据见表2和图2。从表2可以看出,我们的结果与作者的结果非常的接近,其中书上的误差为8.9661%,而我们的误差为8.4582%。

Table 2. Application of the fourth order trend curve in the output of metal cutting machine
表2. 四阶趋势曲线在金属切削机床产量中的应用
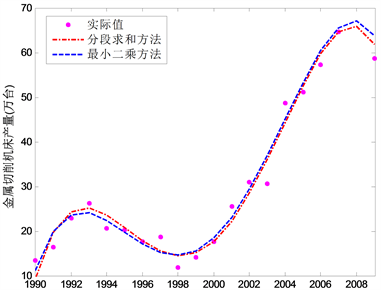
Figure 2. The fourth order trend curve in the output of metal cutting machine
图2. 金属切削机床产量的四阶趋势曲线图
5. 结论
本文讨论了k阶趋势曲线的参数的求解问题,利用分段求和的思想给出了模型中参数的矩阵表达式,并在k = 1和k = 2的情形下给出了模型中参数的具体表达式。进一步,将所提出的方法与相应教材上采用的最小二乘法方法的计算结果进行比较,从计算结果来看,两种的模型精度基本上是一致的。但是,从分析的过程中可以明确知道,我们提出的计算方法更为简单、直接。
NOTES
*通讯作者。