1. 引言
在当下的金融市场中,期权是一种非常重要的金融衍生品,而且期权的定价也一直都是一个非常热门的话题。1973年Black、Scholes以及Merton [1] 共同提出用几何布朗运动来驱动股票的演变过程并推导出了欧式期权的定价公式,即著名的BS公式。由于BS公式极为简便,为此BS模型在金融界和业界都引起了高度的重视,可以说BS模型的提出是金融数学和金融工程界的一次革命。但是,实证研究表明BS模型并非是完美无瑕的,首先,由BS模型所得到期权理论价格同市场的真实价格存在误差并且该误差不是白噪音;其次,BS模型不能解释期权“隐含波动率微笑”的现象;另外,在BS框架下股票的对数收益被假设服从正态分布,这同实际往往存在较大的差异。所以,为了能够让理论更加反应真实的情况,理论研究者用不同的模型来重新对期权的定价进行研究,比如t分布模型 [2] 、GEV模型 [3] 、CGMY模型 [4] 、Heston模型 [5] 以及FMLS模型 [6] 等等。
在众多的修正模型中,FMLS模型是常常被用来驱动股票的动态演变过程,因为该模型能够同时反应期权的隐含波动率微笑以及股票对数收益的分布出现非正态的情况,因此,越来越多的学者在FMLS框架下对金融衍生产品进行了研究。在金融衍生品的定价模型中,数学上为了刻画由FMLS模型中纯跳所引起的非局部性,通常会用一个具有左分数阶导数的偏微分方程来驱动衍生产品价值的变化过程 [7] 。在此基础上,Zhang等 [8] 研究了FMLS框架下的欧式看涨期权,在这篇论文中,作者建立了一个具有二阶数值格式并从理论上对该数值格式进行严格的误差分析和稳定分析。Chen [9] 根据预测校正的思想结合有限元的数值方法对具有FMLS模型的美式看跌期权进行了研究;由于分数阶导数和自由边界的存在使得整个数学模型的求解十分困难,为此在进行求解该模型前,Chen等 [10] 做了相应的坐标变换把自由边界问题变成一个固定边界问题。Wang还利用线性互补的方法来求解FMLS框架下美式期权。Fan [11] 在FMLS框架下研究具有有限到期日的股票抵押定价问题,在这个框架下股票抵押定价的模型是一个具有分数阶的自由边界问题,为了求解该问题,作者引入了一个非线性项的惩罚项以消除自由边界。
为了进一步完备FMLS框架下期权的定价理论,本文研究了该框架下的欧式期权定价问题。我们利用傅里叶变换方法得到欧式看涨期权定价公式并为该公式设计高效的数值算法;另外在此基础上本文还求出了该框架下欧式看涨期权的方差最优对冲策略。为了凸显FMLS模型的优越之处,在论文的最后一部分我们以经典的BS模型作为基础,通过仿真模拟来观察在两个不同模型下欧式期权的价值、隐含波动率以及方差最优对冲策略的差异,并结合相应的经济背景进行深入分析。
2. 欧式期权定价公式
在FMLS框架下,股票价格可以被下面的随机过程所驱动 [6]
(1)
其中r和D分别表示无风险利率和股票的连续红利率,为了方便探讨本文假设
,
是一个非负实数,
,
是一个
稳态的随机变量,并且
,
是凸性调整且
。
根据(1)式,结合文献
稳态的随机变量的性质 [6] 可以得到股票价格对数收益
的特征函数
(2)
其中
为风险中性下的条件期望算子。
设K欧式期权的执行价格,
是如下的FMLS过程
(3)
那么股票的驱动方程(1)式可以转化成下面的形式:
(4)
其中,
。
设
表示欧式看涨期权在时刻t的价值,根据欧式期权的定价原理可知
(5)
其中,
是给定时刻t的信息
,随机变量
的条件密度函数。由随机变量
的定义可知,随机变量
的条件特征函数
可以表示为
再由(2)式可得
(6)
下面我们将以定理的形式给出FMLS框架下欧式看涨期权的定价公式。
定理1假设股票价格
在风险中性测度下满足(4)式,那么以K为执行价格,T为到期日的欧式看涨期权在t时刻的价格
可以表示为
(7)
其中
表示期权合约的剩余时间,
表示复数z的实部,
。
证明 定义一个新函数
其中
是一个大于零的常数且
,那么
若令函数
那么(5)式可以表示为
注意,在
的情况下,函数
是绝对可积的,那么根据卷积定理 [12] 有
其中
表示Fourier变换。于是在(8)式两边同时做Fourier变换,经过简单积分计算可得
上式中的倒数第二个等号应用了Fourier变换的位移性质。接下来在上式两边同时作Fourier逆变换
另外,因为
是映射到实空间的随机变量,那么根据文献 [13] 可知函数
的实部关于
是一个偶函数,虚部关于
是一个奇函数,所以不难发现上式第二个等号右边中括号内是两个共轭复数。于是
下面我们将确定定价公式(7)中的参数
。根据文献 [13] 的结论可知,在公式(7)中参数
必须要让函数
有意义或者不等式
成立,因为在FMLS框架下的资产价格是存在任何阶矩的,所以对于任意的
,不等式
都是成立的,此时按照文献 [13] 的做法,本文取
。
因为本文的理论推导是在假设市场是无套利的前提下的,那么欧式期权的平价公式是成立的,所以对于FMLS框架下欧式看跌期权的定价公式我们直接利用平价公式求得,即
因为
,所以欧式看跌期权在时刻t的价格为
(8)
因为在定价公式(7)中含有一个无穷积分,所以无法在计算上实现,这就需要对该公式中的无穷积分做近似处理。首先,假设A为截断积分的上限,
表示用截断后的公式所计算出来的值,那么如果要是截断误差不高于任意大于0的数
,即
所以只要积分上限A满足
那么欧式看涨期权定价公式(7)的截断误差就不会大于
,那么这时FMLS框架欧式看涨期权的定价公式可以用下面的式子进行近似计算
(9)
其次,我们用梯形公式对(9)进行计算。本文取
,令
,且
,那么(9)式又可以由下面的式子近似地表示
(10)
3. 方差最优对冲策略
根据 [14] 中的结论可知,传统的Delta对冲策略对FMLS框架下的欧式期权不再实用,所以在这部分本文将为FMLS框架的欧式期权设计一个实用的对冲策略。事实上,对冲可以理解为市场参与者通过买卖风险资产来构造资产组合以实现对未定权益终值的一种逼近。逼近程度的优劣通常用均方对冲误差的大小来衡量,即
(11)
其中
,
,
,
,
表示在时刻
期权出售方所持有的风险资产份额,它是一个自融资(self-finance)交易策略。事实上,在(11)中
表示的是在整个期权合约中期权出售方的交易累积收益。在(11)式中方括号内的表达式正好是期权出售方在整个合约内的对冲资产组合,其目的是寻找最优的对冲策略
使得期权金
和交易的累积收益的总和尽可能的接近未定权益终值得贴现
,亦即使对冲资产组合在初始时刻的均方误差
达到最小。接下来,我们就根据这一思想来求出方差最优对冲策略
以及该策略的具体算法。
定理2在风险中性环境下,如果股票价格
满足指数随机过程(4),其中X是一个右连左极的且具有独立增量的随机过程,那么以
为标的资产,K为执行价格,T为到期日且对冲交易时间为
的欧式看涨期权C的方差最优对策略为
(12)
且当
时,
其中
是随机变量
的概率密度函数。当
时
其中
是随机变量
的概率密度函数。
证明因为随机变量X具有稳定的独立增量,且在风险中性概率测度下贴现过程
和
都是鞅,所以由文献 [14] 中的结论可知,FMLS框架下离散时间下欧式看涨期权的对冲均方误差在初始时刻的值可以表示为
显然若要使
值最小,那么对冲策略应该为
(13)
由于随机变量X的分布信息是已知的,所以根据(6)式我们可以把(13)中的分母计算出来,即
又因为
和
都是鞅,所以(13)式子中的分子可以表示为
事实上,在上式中只有
是未知的,接下了我们的目标就是求出这个部分的值。因为
本文记
,那么计算方差最优对冲策略的
就转化为设计
的算法。接下来我们将从
和
两个方面来给出
的计算方法。
1) 先讨论
的时候,亦即
,那么此时
(14)
其中
是给定
的条件下
的条件密度函数。因为在FMLS框架下,股票价格是一个指数Levy过程并且
,也就是说
关于标的资产价格
是单调递减的,所以根据文献 [15] 的结论可知,条件密度函数
满足下面的关系
(15)
其中随机变量
。那么结合(14)和(15)式并且作变量替换
可得
因为
是
随机变量的密度函数,且根据文献 [16] 可知函数
要比指数函数高阶无穷小,所以我们就可以对上式中的无穷积分进行截断,即
(16)
(16)中的最后一步是利用梯形公式而得到的,其中
是截断无穷积分的上限,
。为了保证计算的精度,在数值仿真中本文取
。
2) 接下来考虑
的情况。首先根据重期望公式
(17)
在(17)中
可以直接根据欧式期权看涨公式(10)式得到,即
其中
很显然
是随机变量
的函数,为方便叙述,本文记
,所以
其中a和b是截断无穷积分的下限和上限,且
。至此本文就完成了对定理2的证明。另外,为了保证计算的精度,在数值模拟中本文取
,
,以及
。
4. 数值分析
为了使本文的研究具有说服力,我们将在这个部分进行仿真实验。因为FMLS框架期权的定价公式以及方差最优对冲策略都会涉及到定理1当中的定价公式(7)的近似算法(10)式子,所以再进行仿真模拟前先要对定价公式进行误差检验。因为当
时FMLS模型会退化成为BS模型,所以在检验部分我们分两步来进行,第一步先检验
的情况,第二步检验
的情况。
对于
的情况,固定一组参数:
,把这组数据代入式子(10)当中算出一组值,记为
,然后用经典的BS公式计算出一组值,记为
。在此本文要强调的是,当FMLS模型中的尾部指数
时,
,所以在计算
时,要把经典BS公式中的波动率换成
,即
其中
图1(a)中所呈现的是
和
这两组值关于标的资产的曲线,图1(b)中是这两组值的绝对误差曲线,其定义如下
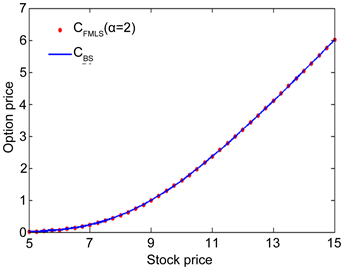 (a) CFMLS (α=2) vs CBS
(a) CFMLS (α=2) vs CBS  (b) 绝对误差图
(b) 绝对误差图
Figure 1. The strike price
图1. 敲定价格
从图1(a)和图1(b)中的曲线不难发现,在相同参数下由BS和FMLS模型得到的欧式期权价值的最大误差不超过0.0042,那么由此可判断本文所推到的FMLS框架下的欧式期权的定价公式在
的情况下是有效的。
由于当
时FMLS框架下的欧式期权的定价公式没有解析表达式,所以本文用蒙特卡洛(Monte Carlo)方法来对公式(4.11)进行检验。不失一般性,我们取
,其他参数
,在用Monte Carlo方法计算期权的价格时,本文采用20000条模拟路径。在图2(a)中红色实线表示由定价公式(10)计算出来的期权的价值,蓝色点则表示由Monte Carlo计算出来的期权的价值;图2(b)中的点则是这两组值得误差(Monte Carlo方法得到的值减去由(10)所得到的值)。由图2(a)和图2(b)中的曲线可知本文所对到的FMLS框架下的欧式期权的定价公式在
的情况下也是有效的。
5. 参数影响分析
在对定价公式进行检验后,接下了本文将结合仿真结果来分析FMLS模型中的参数对期权价值的影响。为了观察尾部指数
对期权价格的影响,本文在图3中呈现了不同
取值下的期权价值关于标的资产价格的曲线。根据图中的曲线可知欧式期权的价值关于
是单调递减的,因为从FMLS模型本身来看,如果
的值越小那么风险资产价格发生跳跃的可能性就会越大,对于持有看涨期权的市场参与者来说就有可能获得更大的收益,所以相应的期权的价值就会更大。
 (a) CFMLS vs Monte Carlo
(a) CFMLS vs Monte Carlo  (b) 误差图
(b) 误差图
Figure 2. The strike price
图2. 敲定价格
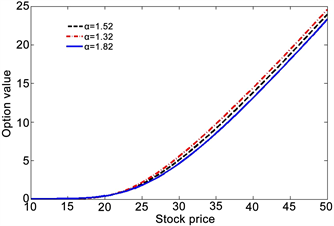
Figure 3. European call value, with
图3. 欧式看涨期权的价值,模型参数
图4中,本文呈现了欧式看涨期权价值在不同参数
下的曲线。由(1)式可知,
决定了股票对数收益分布的离散程度,亦即
的值越大分布就越扩散,那么这就会是期权的价值变大,所以理论上欧式看涨期权的价值关于参数
是单调递增的,而图4中的曲线也正好反应这个事实。
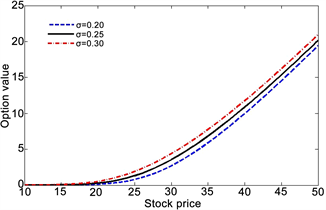
Figure 4. European call value, with
图4. 欧式看涨期权的价值,模型参数
另外为了能够说明FMLS模型能够捕捉欧式期权的隐含波动率,本文从(10)提取出了欧式期权的隐含波动率曲线,如图5(a)和图5(b)所示。由图中的曲线可知,在不同的参数团下期权的隐含波动率曲线都成“微笑”形状,这说明了FMLS模型能够捕捉欧式期权隐含波动率不是一个常数的现象。
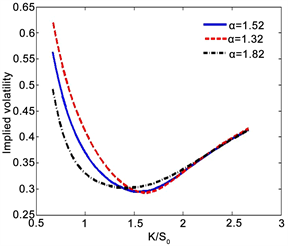 (a) σ=0.2
(a) σ=0.2 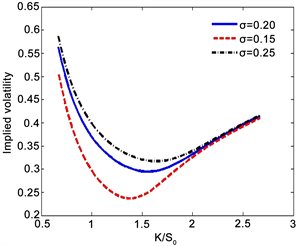 (b) α=1.52
(b) α=1.52
Figure 5. The implied volatility of European call with
图5. 欧式看涨期权的隐含波动率,模型参数
接下来本文将考虑FMLS模型中的两个重要参数
和
对方差最优对冲策略的影响,另外为了作对比我们以BS模型下的Delta对冲策略作为参照,在此需要说明的是著名学者Tonkov [17] 已经证明了在BS框架下方差最优对冲策略和Delta对冲策略是等价的。
图6中所呈现的是BS框架下的Delta对冲策略(BS Delta-Hedging)和FMLS框架下的方差最优对冲策略(FMLS VO-Hedging)曲线,图中的横坐标是期权的价值状态。当期权的价值状态处于价内和平价时,FMLS模型的方差最优对冲策略会高于BS模型的Delta对冲曲线;而在价外时会出现相反的情况。由FMLS和BS模型金融含义可知,投资者在FMLS框架下对股票价格相对较低时会做出较为敏感的反应,即投资者会大量抛售期权,相应的期权出售方也会做出较为相应的调整,所以在这种情况下FMLS框架下的方差最优对冲策略会高于BS框架下Delta对冲;而当股票价格相对较高时投资者在两种框架下的反应恰恰相反,所以当期权处于价外状态时则会出现相反的情况。
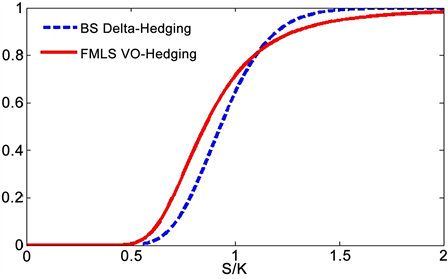
Figure 6. Hedging curve with
图6. 对冲曲线,模型参数
在图7(a)和图7(b)本文分别绘制了不同
和
的取值下方差对冲取的变换趋势。因为
是控制了FMLS随机变量后尾分布和跳跃情况,且当
的值越小厚尾和跳跃现象就越明显,此时期权出售方就会做出较为敏感的调整,如图7(a)所示。另外由于
控制了FMLS模型的尺度参数,即当
越大时FMLS随机变量的分布就越分散,其作用就类似于BS模型当中的波动率,所以当期权的价值状态处于价内和平价是时方差最优对冲策略关于
是单调递减的,当期权的价值状态处于价外时方差最优对冲策略关于
是单调递增的。
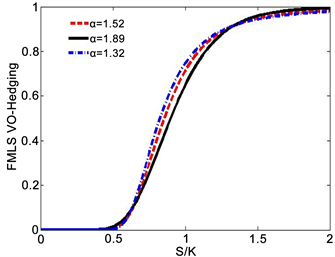 (a) σ=0.2
(a) σ=0.2  (b) α=1.52
(b) α=1.52
图7. FMLS模型的方差最优对冲曲线,模型参数
6. 结论
本文在FMLS框架下研究了欧式期权的定价与方差最优对冲策略。我们利用傅里叶变化的方法得到了欧式看涨期权的定价公式,并设计相应的数值实验对公式进行检验。在此基础上,本文还根据方差最优对冲的原理通过求解一个非线性归划问题得到该框架下欧式看涨期权的方差最优对冲策略。在文章的第五部分,本文以BS模型为基准分析FMLS模型中的重要参数对欧式期权价格和方差最优对冲策略的影响,并根据模型的经济背景解释其经济含义。
基金项目
本文由贵州省科技厅科技计划项目(项目编号:黔科合同基础〔2019〕1175号)以及贵州省贵阳市白云区科技计划项目(项目编号:白科合同〔2017〕37号)资助。