主成分分析与线性判别分析降维比较

Dimension Reduction Comparison between PCA and LDA

摘要: 主成分分析(PCA)和线性判别分析(LDA)是机器学习领域中常用的降维方法。本文针对矩阵型数据结构，将一维的降维方法PCA和LDA推广为二维PCA和二维LDA，2DPCA和2DLDA对矩阵型数据进行降维处理时，克服了维数灾难的问题。实验研究表明，对比降维效果和分类错误率，2DLDA相比2DPCA是一种更为出色的降维分类方法。

Abstract: Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) are commonly used in machine learning. In this paper, we extend PCA and LDA to 2DPCA and 2DLDA, 2DPCA and 2DLDA are directly to reduce the dimension on the original matrix data structure, overcoming the problem of the curse of dimensionality. Empirical research suggests that 2DLDA is a better dimensionality reduction classification method than 2DPCA compared with the effect of dimension reduction and the error rate of classification.

1. 引言

在数据降维处理中 [1]，比较常用的方法为线性变换技术。即通过线性投影将原样本数据投影到低维子空间中，其中典型的有PCA与LDA。PCA的意义是在重构时其平方误差最小；LDA是一种有监督的线性降维算法 [2]，其基本思想是选择使得Fisher准则函数达到极值的向量作为最佳投影方向，从而使得样本在该方向上投影后，达到最大的类间散布距离和最小的类内散布距离。PCA和LDA的不同之处在于，无监督的PCA能保持数据信息，而LDA是使降维后的数据点尽可能地容易被区分。

针对矩阵型的数据结构，我们将一维的降维方法PCA和LDA在矩阵模式上推广为二维PCA和二维LDA。采用二维降维方法2DPCA和2DLDA，其最大的优势于是不需要将高数据转化向量，克服了维数灾难 [3]。

本文将在真实的两个数据集上，验证在不同的多元时间序列数据集下，2DPCA和2DLDA两种数据降维方法效果的优劣。

2. 研究方法概述

本节分别介绍二维主成分分析(2DPCA)算法，二维线性判别分析(2DLDA)算法。

2.1. 二维主成分分析(2DPCA)算法

令 $X={\left\{x_i\right\}}_{i=1}^N$ 是一组样本， $x_i\in {ℝ}^{r\times c}$，则样本平均值为：

$\bar{X}=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{x}_i}$ (1)

定义协方差矩阵为 $G$ ：

$G=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}\left(x_i-\bar{X}\right){\left(x_i-\bar{X}\right)}^T}$ (2)

其中 $G$ 为 $r\times r$ 的非负定矩阵。对 $G$ 进行特征值分解，最大的 $d$ 个特征值所对应的标准正交的特征向量构成投影向量组 $U=\left(u_1,\cdots ,u_d\right)$。

2.2. 二维线性判别分析(2DLDA)算法

令 $X={\left\{x_i\right\}}_{i=1}^N$ 是一组样本， $x_i\in {ℝ}^{r\times c}$，其中 $X$ 分为 ${\pi }_i\left(i=1,2,\cdots ,k\right)$ 类， $n_i$ 为第 $i$ 类样本的个数，

则样本均值为：

$\bar{X}=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{N}{\sum }}{x}_i}$ (3)

第 $i$ 类样本的类内平均：

${\bar{X}}_{{\pi }_i}=\frac{1}{n_i}{\displaystyle \underset{x_j\in {\pi }_i}{\overset{n_i}{\sum }}{x}_j}$ (4)

定义如下类间散步矩阵：

$S_b=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{k}{\sum }}{n}_i\left({\bar{X}}_{{\pi }_i}-\bar{X}\right){\left({\bar{X}}_{{\pi }_i}-\bar{X}\right)}^{\prime }}$ (5)

类内散布矩阵：

$S_w=\frac{1}{N}{\displaystyle \underset{i=1}{\overset{k}{\sum }}{\displaystyle \underset{x\in {\pi }_i}{\sum }\left(x-{\bar{X}}_{{\pi }_i}\right){\left(x-{\bar{X}}_{{\pi }_i}\right)}^{\prime }}}$ (6)

2DLDA寻找的最佳投影矩阵 $U$ ：

$J\left(U\right)=\frac{U^{\prime }{S}_{b}U}{U^{\prime }{S}_{w}U}$。 (7)

3. 实证分析

本节将在Wafer、Ausla这两个真实的数据集，验证在不同的数据集下，2DPCA和2DLDA两种数据降维方法效果的优劣。

3.1. 数据集介绍

3.1.1. Wafer数据集

Wafer数据集是由一个真空传感器应用一个硅晶片在刻画中记录下来的。该数据集记录的晶片类型分为两个类型：“正常”与“不正常”。其中“正常”类型的样本数为1067个，“不正常”类型的样本数为127个。

3.1.2. AUSLAN数据集

AUSLAN数据集有2565个数据样本，包含95个语音信号，每个信号由27个样本组成，其中每个样本的长度在47到95之间。每一个样本有22个变量，记录了这25个由当地人发音的语音信息。

2个数据集描述见表1所示。

Table 1. Data set description summary

表1. 数据集描述汇总

3.2. 降维效果

为了降低实验结果的变化性，我们在每次数据集上重复5次实验，下面分别给出了各个数据集2DPCA和2DLDA的实验结果。

3.2.1. Wafer数据集上的实验效果

Table 2. Error rate results and dimension reduction results of 2DPCA and 2DLDA on Wafer dataset

表2. 2DPCA和2DLDA在Wafer数据集上的错误率结果和降维结果

表2给出了2DPCA和2DLDA在Wafer数据集上的5次实验的错误率结果和降维结果。由表2可知，相比较，2DPCA的降维效果比2DLDA的降维效果好，但2DPCA的分类错误率比2DLDA的高。图1直观呈现出两种方法实验的分类错误率。

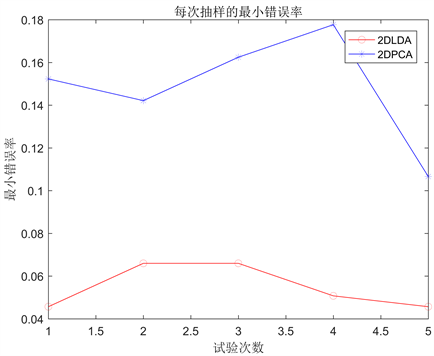
Figure 1. Error rates of 2DPCA and 2DLDA on wafer datasets

图1. 2DPCA和2DLDA在wafer数据集上的错误率

3.2.2. AUSLAN数据集上的实验效果

Table 3. Error rate results and dimensionality reduction results of 2DPCA and 2DLDA on the AUSLAN dataset

表3. 2DPCA和2DLDA在AUSLAN数据集上的错误率结果和降维结果

表3给出了2DPCA和2DLDA在AUSLAN数据集上的5次实验的错误率结果和降维结果。由表3可知，相比较，2DPCA的降维效果与2DLDA的降维效果差别不大，但2DPCA的分类错误率明显比2DLDA的高。图2直观呈现出两种方法实验的分类错误率。

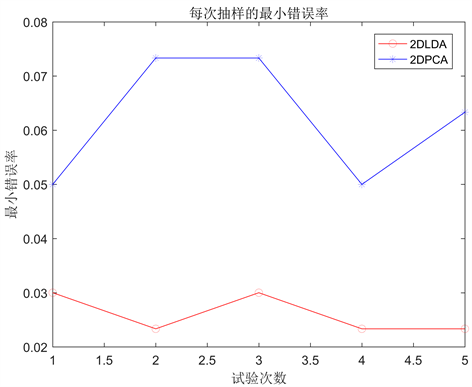
Figure 2. Error rates of 2DPCA and 2DLDA on the AUSLAN dataset

图2. 2DPCA和2DLDA在AUSLAN数据集上的错误率

4. 结论

通过提取2DPCA和2DLDA分别在wafer、Auslan这两个真实的数据集上的最小错误率，我们确定了用不同方法进行降维的最佳维数，通过每种方法降维的最佳维数提取了与之相对应的错误率，最后我们求出相应的平均错误率，如表4所示。

Table 4. Average classification error rate results and dimensionality reduction results of 2DPCA and 2DLDA on 3 datasets

表4. 2DPCA和2DLDA在3个数据集上的平均分类错误率结果和降维结果

由表4可知：2DLDA的平均分类错误率均小于2DPCA。这说明判别分析的分类效果要优于主成分分析的分类效果。因此，综合降维效果和分类错误率这两个因素，对比实验证实了2DLDA相比2DPCA是一种更为出色的分类方法。