农村居民人均可支配收入的分析

Analysis of Per Capita Disposable Income of Rural Residents

摘要: 通过分析，找到影响农村居民人均可支配收入的因素，利用逐步回归法建立线性模型，通过回归系数的显著性检验，可以找到影响农村居民人均可支配收入的显著因素。对于自变量之间的多重共线性，利用主成分回归或者岭回归消除自变量之间的共线性，建立岭回归的回归方程y=49.504+0.432x₁+0.142x₂-0.549x₃。绘制农村居民人均可支配收入与时间的序列图，发现农村居民人均可支配收入呈上升趋势，根据差分后的数据建立ARMA(p,q)模型，将趋势提取出来。

Abstract: Through the analysis, the factors affecting the per capita disposable income of rural residents are found, and a linear model is established by using the stepwise regression method. Through the significance test of the regression coefficient, the significant factors affecting the per capita disposable income of rural residents can be found. For multicollinearity among independent variables, principal component regression or ridge regression is used to eliminate the collinearity among independent variables, and the regression equation of ridge regression is established y=49.504+0.432x₁+0.142x₂-0.549x₃. Draw a sequence diagram of the per capita disposable income and time of rural residents, and find that the per capita disposable income of rural residents is on the rise. Build a model ARMA(p,q) based on the data after the difference and extract the trend.

1. 引言

通过分析找到影响农村居民人均可支配收入的显著性因素并建立线性回归模型，检查自变量之间的多重共线性并消除，在使用主成分分析消除多重共线性建立模型时，农业各税回归系数的符号不符合实际，尝试使用岭回归建立模型后，回归系数的正负号得到解决，多重共线性也已消除；农村居民人均可支配收入随时间的变化呈上升趋势，可建立模型，将趋势项提取出来。

2. 材料与方法

2.1. 线性回归模型的介绍 [1]

根据搜集的数据，建立线性回归模型，进行回归方程以及回归系数的检验，分析影响农村居民人均可支配收入的因素有哪些；若模型存在共线性，则使用主成分分析方法消除共线性进一步建立模型。根据时间发生的顺序将农村居民人均可支配收入在多个时刻的数值记录下来，以得到一时间序列，建立时间序列的模型，分析农民收入的变化趋势。

2.1.1. 线性回归模型的确立

设随机变量y与一般变量 $x_1,x_2,\cdots ,x_p$ 的线性回归模型为

$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_p{x}_p+\epsilon$

式中， ${\beta }_0,{\beta }_1,\cdots ,{\beta }_p$ 是 $p+1$ 个未知参数， ${\beta }_0$ 称为回归常数， ${\beta }_1,\cdots ,{\beta }_p$ 称为回归系数。y称为解释变量(因变量)， $x_1,x_2,\cdots ,x_p$ 是p个可以精确测量并控制的一般变量，称为解释变量(自变量)。

$\epsilon$ 是随机误差，并且假定

$\{\begin{array}{l}E\left(\epsilon \right)=0\hfill \\ \mathrm{var}\left(\epsilon \right)={\sigma }^2\hfill \end{array}$

2.1.2. 回归参数的普通最小二乘估计

即寻找参数 ${\beta }_0,{\beta }_1,\cdots ,{\beta }_p$ 的估计值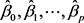，使离差平方和 $Q\left({\beta }_0,{\beta }_1,\cdots ,{\beta }_p\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-{\beta }_0-{\beta }_1{x}_{i1}-\cdots -{\beta }_p{x}_{ip}\right)}^2}$ 达到极小。

当 ${\left(X^{\prime }X\right)}^{-1}$ 存在时，即得回归参数的最小二乘估计为：

$\hat{\beta }={\left(X^{\prime }X\right)}^{-1}{X}^{\prime }y$

2.1.3. 回归方程、回归系数的检验

对多元线性回归方程的显著性检验就是要看自变量 $x_1,x_2,\cdots ,x_p$ 从整体上对随机变量y是否有明显的影响。

原假设 $H_0:{\beta }_1={\beta }_2=\cdots ={\beta }_p=0$

构造F检验统计量如下：

当原假设成立时，F服从自由度为 $\left(p,n-p-1\right)$ 的F分布。

当 $F>F_{\alpha }\left(p,n-p-1\right)$ 时，拒绝原假设 $H_0$，否则认为在显著性水平 $\alpha$ 下，y与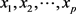有显著的线性关系，即回归方程是显著的。

检验 $x_j$ 是否显著等价于检验

$H_{0j}:{\beta }_j=0,j=1,2,\cdots ,p$

如果接受原假设，则 $x_j$ 不显著；如果拒绝原假设，则 $x_j$ 是显著的。

据此可以构造t统计量

$t_j=\frac{\hat{\beta }}{\sqrt{c_{jj}}\hat{\sigma }}$

式中

$\hat{\sigma }=\sqrt{\frac{1}{n-p-1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{e}_i^2}}$

2.1.4. 共线性诊断

① 方差扩大因子法

$c_{jj}=\frac{1}{1-R_j^2}$ 作为方差扩大因子的定义，证明见参考文献 [2]，当 $VI{F}_j\ge 10$ 时，说明自变量 $x_j$ 与其余自变量之间有严重的多重共线性。(注意：有些教材认为 $VI{F}_j\ge 4$ 存在多重共线性。详见参考文献 [3])。

② 条件数

记 $X^{\prime }X$ 的最大特征根为 ${\lambda }_m$，称

$k_i=\sqrt{\frac{{\lambda }_m}{{\lambda }_i}},i=0,1,\cdots ,p$

为特征根 ${\lambda }_i$ 的条件数。

通常认为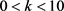时，设计矩阵X没有多重共线性； $10\le k<100$ 时，存在较强的多重共线性； $k\ge 100$ 时，存在严重的多重共线性。

2.1.5. 主成分的定义与导出 [4]

设X是p维随机变量，并假设 $\mu =E\left(X\right)$， $\sum =\mathrm{var}\left(X\right)$。考虑如下线性变换

$\{\begin{array}{l}{Z}_1=a_1^{\text{T}}X\\ Z_2=a_2^{\text{T}}X\\ ⋮\\ Z_p=a_p^{\text{T}}X\end{array}$

易见

$\mathrm{var}\left(Z_i\right)=a_i^{\text{T}}\sum a_i,i=1,2,\cdots ,p$

$\mathrm{cov}\left(Z_i,Z_j\right)=a_i^{\text{T}}\sum a_j,i,j=1,2,\cdots ,p,i\ne j$

我们希望 $Z_1$ 的方差达到最大，即是约束优化问题

$\max a^{\text{T}}\sum a$

$\text{s}\text{.t}\text{.}{a}^{\text{T}}a=1$

的解。因此， $a_1$ 是 $\sum$ 最大特征值(不妨设为 ${\lambda }_1$ )的特征向量。此时，称 $Z_1=a_1^{\text{T}}X$ 为第一主成分。类似地，希望 $Z_2$ 的方差达到最大，并且要求 $\mathrm{cov}\left(Z_1,Z_2\right)=a_1^{\text{T}}\sum a_2=0$。由于 $a_1$ 是 ${\lambda }_1$ 的特征向量，所以，选择的 $a_2$ 应与 $a_1$ 正交。类似于前面的推导， $a_2$ 是 $\sum$ 第二大特征值(不妨设为 ${\lambda }_2$ )的特征向量。称 $Z_2=a_2^{\text{T}}X$ 为第二主成分。

一般情况下对于协方差阵 $\sum$，存在正交阵Q，将它化为对角阵，即

$Q^{\text{T}}\sum Q=\Lambda =diag\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_p\right)$

且 ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_p$，则矩阵Q的第i列就对应于 $a_i$，相应的 $Z_i$ 为第i主成分。

2.2. ARMA模型

设 $\left\{{\epsilon }_t:t=0\pm 1,\pm 2,\cdots \right\}~WN\left(0,{\sigma }_{\epsilon }^2\right)$，则序列 $\left\{X_t:t=0\pm 1,\pm 2,\cdots \right\}$ 满足的p阶常系数线性差分方程

$X_t={\varphi }_0+{\varphi }_1{X}_{t-1}+\cdots +{\varphi }_p{X}_{t-p}+{\epsilon }_t-{\theta }_1{\epsilon }_{t-1}-\cdots -{\theta }_q{\epsilon }_{t-q}\text{,}t=0\pm 1,\pm 2,\cdots$

为p阶自回归q阶移动平均模型，记为 $\text{ARMA}\left(p,q\right)$ 模型。其中 ${\varphi }_p,{\theta }_q\ne 0$，关于 $\lambda$ 的代数方程 ${\lambda }^p-{\varphi }_1{\lambda }^{p-1}-\cdots -{\varphi }_{p-1}\lambda -{\varphi }_p=0$ 与 ${\lambda }^q-{\theta }_1{\lambda }^{q-1}-\cdots -{\theta }_{q-1}\lambda -{\theta }_p=0$ 无公共根。称 ${\varphi }_0=0$ 的模型为中心化 $\text{ARMA}\left(p,q\right)$ 模型。

利用延迟算子B可将模型表示为

$\Phi \left(B\right)X_t={\varphi }_0+\Theta \left(B\right){\epsilon }_t,t=0,\pm 1,\pm 2,\cdots$

其中 $\Phi \left(B\right)=1-{\varphi }_{1}B-{\varphi }_2{B}^2-\cdots -{\varphi }_p{B}^p$ 和 $\Theta \left(B\right)=1-{\theta }_{1}B-{\theta }_2{B}^2-\cdots -{\theta }_q{B}^q$ 分别为B的p和q次多项式。

$\text{AR}\left(p\right)$ 序列的偏自相关系数是p阶截尾的； $\text{MA}\left(q\right)$ 序列的自相关系数是q阶截尾的。

3. 结果与分析

3.1. 回归方程的建立

根据统计年鉴搜集能够影响农村居民人均可支配收入的因素的数据。其中农村居民人均可支配收入作为因变量，农产品生产价格指数、受灾面积、耕地面积、支农支出、农业各税、农业机械总动力、农用化肥施用量、乡村就业人数、农业产值作为自变量。

3.1.1. 建立回归方程

使用SPSS软件建立回归方程。由于自变量个数较多，我们采用逐步回归法建立线性回归方程，进行回归方程、回归系数的检验以及共线性诊断等。回归方程的检验见图1~3。

若记y为农村居民人均可支配收入， $x_1$ 为支农支出， $x_2$ 为农业产值， $x_3$ 为农业各税，由图3可以建立回归方程

$y=20.213+0.450x_1+0.146x_2-0.627x_3$

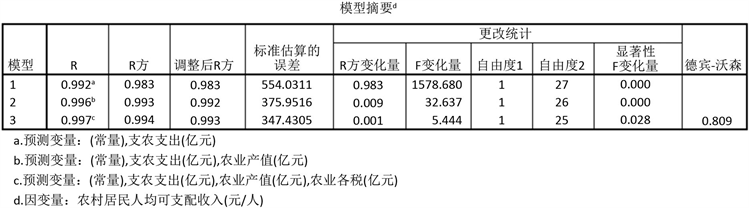
Figure 1. Summary of each model of stepwise regression method

图1. 逐步回归法的各模型摘要

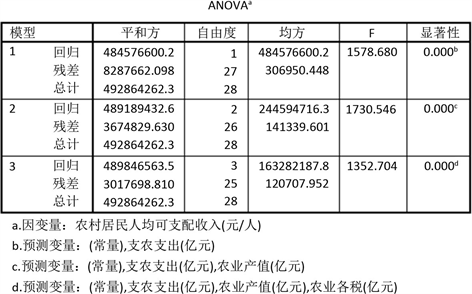
Figure 2. Analysis of variance of each model by stepwise regression method

图2. 逐步回归法的各模型方差分析

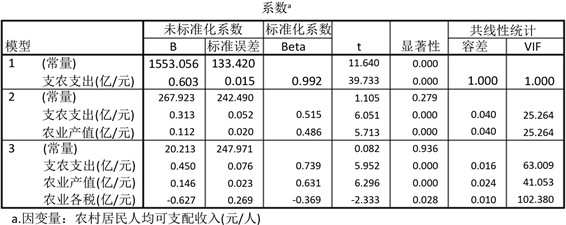
Figure 3. Coefficient value, test and collinearity diagnosis of regression equation

图3. 回归方程的系数取值、检验及共线性诊断

由图1可知：回归方程的 $R^2=0.994$，回归方程的p值小于 $\alpha \left(0.05\right)$，回归方程是显著的；回归系数也都小于 $\alpha$，因此回归系数也是显著的，显然使用线性回归方程去拟合模型是较好的。

但上图也可以看到，自变量 $x_1,x_2,x_3$ 之间存在共线性，若能够消除共线性，则模型将会进一步改善。

3.1.2. 主成分分析消除共线性

由图4可知，第一个主成分的累计贡献率以达到99%，另外两个主成分可以舍去，达到降维的目的。

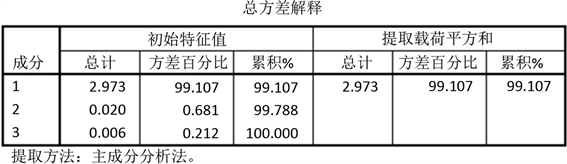
Figure 4. Cumulative contribution rate of variance

图4. 方差的累计贡献率

为获得因变量y与自变量 $x_1,x_2,x_3$ 的回归方程，可以使用spss分两次进行线性回归得到；也可使用R软件编程一步得到。

下面为简化过程，我们利用R软件进行求解。

Table 1. The regression coefficients solved by using R

表1. 利用R求解的回归系数

因此，由表1可知，还原后的主成分回归方程为

$y=558.468+0.203x_1+0.077x_2+0.566x_3$

通过分析可以发现，农业各税与农村居民人均可支配收入是负相关的，因此，回归系数应该为负，但由回归方程可知，各自变量对因变量的影响都是正的，这显然与实际不符。

3.1.3. 岭回归

尝试使用岭回归进行回归方程系数的估计。绘制的岭迹图见图5。

Figure 5. Ridge trace

图5. 岭迹图

Figure 6. Estimation of ridge regression coefficient

图6. 岭回归系数估计

由图6可知岭回归的回归系数，建立的回归方程为

$y=49.504+0.432x_1+0.142x_2-0.549x_3$

显然，此问题使用岭回归能较好的建立回归方程。

从以上结果可知，影响农村居民人均可支配收入的因素有三个，分别是支农支出、农业产值、农业各税。其中，支农支出、农业产值对农村居民人均可支配收入的影响是正相关的，农业各税对农村居民人均可支配收入的影响是负相关的。

3.2. 农民收入的变化趋势

3.2.1. 描述性时序分析

从图7上来看，农村居民人均可支配收入呈上升趋势，可根据自相关以及偏自相关图确定模型。

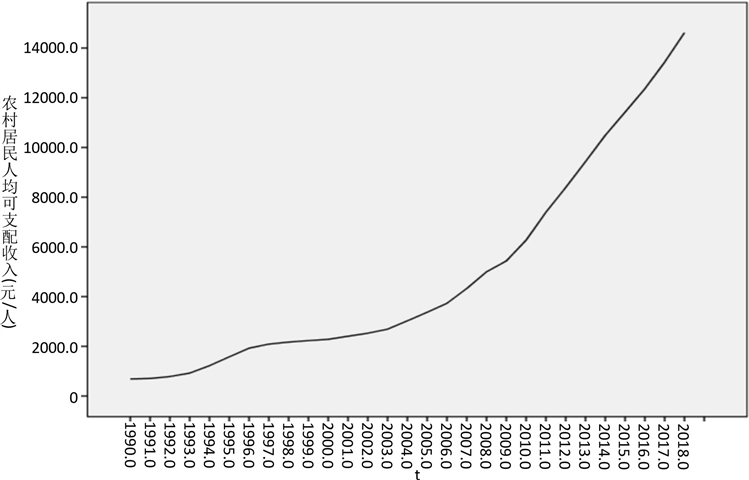
Figure 7. Time series of per capita disposable income of rural residents

图7. 农村居民人均可支配收入的时序图

3.2.2. ARMA模型

二阶差分后的时序图(图8)平稳，根据差分后的自相关图以及偏自相关图，可以建立差分后 $\text{AR}\left(1\right)$ 模型(见图9)。

Figure 8. Sequence diagram after second-order difference

图8. 二阶差分后的时序图

Figure 9. Model parameters in $\text{ARIMA}\left(1,2,0\right)$

图9. $\text{ARIMA}\left(1,2,0\right)$ 的模型参数

因此，可建立方程

${\nabla }^2{X}_t=23.204+0.130{\nabla }^2{X}_{t-1}+{\epsilon }_t$

根据图10，可以看到模型的拟合效果。进而也可以进行数据的预测。

4. 讨论

4.1. 回归方程的参数解释

支农支出是指国家对农业、农村、农民的财政支持，显然，财政支出越大，农民的收入也越高；

农业产值能够反映农民一年的生产规模，农业产值越大，农民收入越高；

Figure 10. Fitting effect of the model

图10. 模型的拟合效果

农业各税包括耕地占用税、契税等，是国家对从事农业生产、有农业收入的单位和个人征收的一种税，农业各税越高，农民收入越低。

以上分析可以发现，国家加大对农业的支出、提高农业产值以及降低农业税可以有效地提高农民的收入。

4.2. 预测

通过建立线性回归模型、 $\text{ARIMA}\left(1,2,0\right)$，可对农村居民人均可支配收入进行预测，求解置信区间等等。

4.3. 模型分析

不同时期影响农村居民人均可支配收入的因素是不太相同的，不同国家、不同地区也是不同的，要想对一个地区影响农民收入的因素进行分析，需要重新获取数据，重新分析，但分析的基本想法是不变的。

附录：R程序代码

install.packages(car)

install.packages(MASS)

install.packages(lars)

library(foreign)

library(car)

library(MASS)

library(lars)

data <- read.csv(数据.CSV)

data<-na.omit(data)

data1<-data[c(6,7,11,12)]

lm.sol <- lm(y~x1+x2+x3,data=data1)

summary(lm.sol)

student.pr <- princomp(~x1+x2+x3,data=data1,cor=T)

summary(student.pr,loadings=TRUE)

pre <-predict(student.pr)

data1$z<-pre[,1]

lm.sol <- lm(y~z,data=data1)

summary(lm.sol)

data1$z <-pre[,1]

student.pr <- princomp(~x1+x2+x3,data=data1,cor=T)

summary(student.pr,loadings=TRUE)

beta <-coef(lm.sol)

A<-loadings(student.pr)

x.bar <-student.pr$center

x.sd <- student.pr$scale

coef <- (beta[2]*A[,1])/x.sd

beta0 <- beta[1]-sum(x.bar*coef)

c(beta0,coef)

#绘制岭迹图

plot(lm.ridge(y~x1+x2+x3,

data=data1,lambda=seq(0,3,0.001)))

select(lm.ridge(y~x1+x2+x3,

data=data1,lambda=seq(0,0.3,0.001)))

#利用select 函数找出最优岭参数lambda,会有三个值，任选一个即可。

lm.ridge(y~x1+x2+x3,data=data1,lambda=0.013)

#把选取的lmbda参数写到岭回归函数中去，在这里lambda=0.013。