一类随机微分动力系统的转移概率密度函数的研究

Study on the Transfer Probability Density Function of a Class of Stochastic Differential Dynamical Systems

摘要: 本文探究了一类随机动力系统转移概率密度函数的求解及其有效性问题。首先，提出了一种计算简便、精度较高的数值模拟方法，用于得到FPK (Fokker-Planck-Kolmogorov)方程的近似解。其次，通过比较该近似解与系统的精确解，我们发现此模拟方法的相对误差保持在2 × 10⁽⁻³⁾以内，误差基本在10⁽⁻³⁾以内。最后，通过比较由近似解得到的状态变量出现在某一稳态区域的概率和系统离散后的相图，我们得出此模拟方法可以有效地描述系统的性态。因此，它是求解系统FPK方程的一种有效算法。

Abstract: In this paper, the solution and validity of the transfer probability density function for a class of stochastic dynamical systems are investigated. Firstly, a simple and accurate numerical simulation method is proposed to obtain the approximate solution of FPK (Fokker-Planck-Kolmogorov) equation. Secondly, by comparing the approximate solution with the exact solution of the system, we found that the relative error of this simulation method is less than 2 × 10⁽⁻³⁾ and the error is basically within 10⁽⁻³⁾. Finally, by comparing the probability that the state variables obtained by the approximate solution appear in a steady-state region with the phase diagram of the discrete system, we conclude that the simulation method can effectively describe the system’s behavior. Therefore, it is an effective algorithm to solve the FPK equation of the system.

1. 引言

对随机微分动力系统而言，研究FPK方程是探究系统响应的一种重要方法。通过求解FPK方程，我们可以得到状态变量的转移概率密度函数，进而了解系统的状态。但是对于绝大多数系统而言，其FPK方程无法或很难求得其精确解，因此，FPK方程的数值解法非常重要。在许多学者的共同努力下，目前已经出现许多近似解法，例如有限元法 [1]，路径积分法 [2] [3] [4]，有限差分法 [5] [6] [7] [8] [9]，高斯闭合法 [10] - [16] 等等，但极少数文章关注其精确度。所以，本文针对一类非线性随机动力系统，在现有文献的基础上，首先提出一种数值解法——指数闭合法 [15]，其次研究其精确性问题。

我们的想法是：针对一类非线性随机动力系统，首先写出系统的FPK方程，其次假设方程的近似解为指数多项式形式，利用待定系数法可以求解出近似解的系数，从而得到系统FPK方程的数值解。并且，我们从两个方面验证该方法的有效性：一方面，比较该方法得到的FPK方程的数值解和广义平稳条件下的精确解的误差，发现该解法的误差小于千分之三。另一方面，比较数值解对应的转移概率密度函数和系统离散化后的相图这两者所确定的稳态区域，发现两个区域具有高度一致性。因此，本文提出的数值解法不仅计算简便，而且精度较高，是求解FPK方程的一种有效方法。

2. 数值算法

2.1. 准备工作

对于一般的非线性随机动力系统 [17]：

$\frac{\text{d}{X}_i}{\text{d}t}=f_i\left(X\right)+{\displaystyle \underset{l=1}{\overset{m}{\sum }}{g}_{il}}\left(X\right)W_l\left(t\right),i=1,2,\cdots ,n$ (1)

式中 $X\left(t\right)={\left[x_1,x_2,\cdots ,x_n\right]}^{\text{T}}$， $W_l\left(t\right)$ 是高斯白噪声，其相关函数为

$E\left[W_l\left(t\right)W_s\left(t+\tau \right)\right]=2\pi K_{ls}\delta \left(\tau \right),l,s=1,2,\cdots ,m$ (2)

如果该系统存在平稳转移概率密度函数，则由下列简化FPK方程决定：

${\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\partial }{\partial x_i}{G}_i}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{\partial }{\partial x_i}\left[a_i\left(x\right)p-\frac{1}{2}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{\partial }{\partial x_j}}\left(b_{ij}\left(x\right)p\right)\right]}=0$ (3)

式中G_i是第i个方向的概率流。a_i、b_ij分别是一、二阶导数矩，由方程(1)可导出：

$\begin{array}{l}{a}_i\left(x\right)=f_i\left(x\right)+\pi {\displaystyle \underset{k=1}{\overset{n}{\sum }}{\displaystyle \underset{l,s=1}{\overset{m}{\sum }}{K}_{ls}{g}_{ks}}}\left(x\right)\frac{\partial }{\partial x_k}{g}_{il}\left(x\right);\\ b_{ij}\left(x\right)=2\pi {\displaystyle \underset{l,s=1}{\overset{m}{\sum }}{K}_{ls}{g}_{il}\left(x\right)g_{js}\left(x\right)};\end{array}$ (4)

如果对(3)增加如下一组充分条件，我们可以得到系统(1)在广义平稳条件下的精确解：

$G_i=a_i\left(x\right)p-\frac{1}{2}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{\partial }{\partial x_j}}\left[b_{ij}\left(x\right)p\right]=0$ (5)

此时，系统(1)属于平稳势类，因此，我们可以将平稳转移概率密度函数表示为 $p\left(x\right)=C\exp \left[-\phi \left(x\right)\right]$。其中，C是归一化常数， $\phi \left(X\right)$ 叫做概率势函数。

而广义平稳的条件只有极少数系统满足，绝大多数系统的FPK方程无法或很难求解。下面我们对本文的数值算法思想进行详细阐述。

2.2. 算法简述

我们假设系统(1)的FPK方程的解，即系统的平稳转移概率密度函数为如下形式：

$p_n\left(x\right)=C\exp \left[a_{11}{x}_1+a_{12}{x}_2+a_{21}{x}_1^2+a_{22}{x}_1{x}_2+a_{23}{x}_2^2+\cdots +a_{ij}{x}_1^{i-j+1}{x}_2^{j-1}+\cdots +a_{nn+1}{x}_2^n\right]$ (6)

其中C为归一化常数 $a_{11},a_{12},\cdots ,a_{nn+1}\left(n\ge 2\right)$ 是常数。由于解必须要满足方程，即上式需满足(3)，从而我们将上式带入(3)，得到：

$a_i\left(x\right)p_n-\frac{1}{2}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{\partial }{\partial x_j}}\left[b_{ij}\left(x\right)p_n\right]=0$ (7)

对上式两边使用待定系数法，通过解方程便可求出 $x_1^i,x_2^j\left(i,j=0,\cdots ,n\right)$ 的系数 $a_{11},a_{12},\cdots ,a_{nn+1}\left(n\ge 2\right)$ 与归一化常数C。因此，我们就可得到FPK方程的数值解。

下一小节我们通过两个例子具体说明该算法的计算过程与有效性。

3. 应用

3.1. 例1

考虑：

$\ddot{x}+2\alpha \left[1+W_1\left(t\right)\right]\stackrel{\dot{}}{x}+{\omega }^2\left[1+W_2\left(t\right)\right]x+{\beta }_1\left(x^2+\frac{{\stackrel{\dot{}}{x}}^2}{{\omega }^2}\right)\stackrel{\dot{}}{x}=W_3\left(t\right)$ (8)

式中 $W_1\left(t\right),W_2\left(t\right),W_3\left(t\right)$ 是相互独立的Stratonovich意义下的零均值高斯白噪声过程，其谱密度常数分别是 $k_1,k_2,k_3$。 $\alpha ,\omega ,{\beta }_{\text{1}}$ 是常数。

令 $x_1=x,x_2=\stackrel{\dot{}}{x}$，则可得到其Stratonovich型随机微分方程为：

$\{\begin{array}{l}\text{d}{x}_1=x_2\text{d}t\\ \text{d}{x}_2=\left[-2\alpha x_2-{\omega }^2{x}_1-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2\right]\text{d}t-2\alpha x_2\sqrt{2\pi k_1}\circ \text{d}{B}_1\left(t\right)\\ -{\omega }^2{x}_1\sqrt{2\pi k_2}\circ \text{d}{B}_2\left(t\right)+\sqrt{2\pi k_3}\circ \text{d}{B}_3\left(t\right)\end{array}$ (9)

加入Wong-Zakai 修正项，上述方程便转化成Itô型随机微分方程为：

$\{\begin{array}{l}\text{d}{x}_1=x_2\text{d}t\\ \text{d}{x}_2=\left[-2\alpha x_2-{\omega }^2{x}_1-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2+4{\alpha }^2{x}_2\pi k_1\right]\text{d}t-2\alpha x_2\sqrt{2\pi k_1}\text{d}{B}_1\left(t\right)\\ -{\omega }^2{x}_1\sqrt{2\pi k_2}\text{d}{B}_2\left(t\right)+\sqrt{2\pi k_3}\text{d}{B}_3\left(t\right)\end{array}$ (10)

我们求出一、二阶导数矩分别为：

$\begin{array}{l}{a}_1=x_2;a_2=-2\alpha x_2-{\omega }^2{x}_1-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2+4{\alpha }^2{x}_2\pi k_1;\\ b_{11}=b_{12}=b_{21}=0;b_{22}=8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3;\end{array}$ (11)

带入(3)便可得到此系统的FPK方程：

$\begin{array}{l}\frac{\partial x_{2}p}{\partial x_1}+\frac{\partial \left[-2\alpha x_2-{\omega }^2{x}_1-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2+4{\alpha }^2{x}_2\pi k_1\right]p}{\partial x_2}\\ -\frac{1}{2}\frac{{\partial }^2\left[8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right]p}{\partial x_2^2}=0\end{array}$ (12)

我们知道，通过将一阶导数矩分为可逆和不可逆分量可以将精确可解类从平稳势拓展到详细平衡。类似思路，我们不仅把一阶导数矩分开，而且把二阶导数矩也分开，将精确可解类进一步拓展，用于求解系统的FPK方程。(12)式左端最后一项可以写成：

$\begin{array}{l}\frac{{\partial }^2\left[8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right]p}{\partial x_2^2}\\ =\frac{\partial \left[16{\alpha }^2{x}_2\pi k_{1}p\right]}{\partial x_2}+\frac{\partial \left[\left(8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right)\frac{\partial p}{\partial x_2}\right]}{\partial x_2}\end{array}$ (13)

将上式带入FPK方程(12)，我们可以得到：

$\begin{array}{l}\frac{\partial x_{2}p}{\partial x_1}-{\omega }^2{x}_1\frac{\partial p}{\partial x_2}+\frac{\partial \left[-2\alpha x_2-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2-4{\alpha }^2{x}_2\pi k_1\right]p}{\partial x_2}\\ -\frac{1}{2}\frac{\partial \left[\left(8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right)\frac{\partial p}{\partial x_2}\right]}{\partial x}=0\end{array}$ (14)

为了化简上式的求解，我们加入如下一组充分条件：

$\{\begin{array}{l}\frac{\partial x_{2}p}{\partial x_1}-{\omega }^2{x}_1\frac{\partial p}{\partial x_2}=0\\ \left[-2\alpha x_2-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2-4{\alpha }^2{x}_2\pi k_1\right]p-\frac{1}{2}\left(8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right)\frac{\partial p}{\partial x_2}=0\end{array}$ (15)

假设 $p\left(x\right)=C\exp \left[-\phi \left(x\right)\right]$，其中 $\phi \left(x\right)=\phi \left(\lambda \right),\lambda =\frac{1}{2}{x}_2^2+\frac{1}{2}{\omega }^2{x}_1^2$，C是归一化常数。则(15)式等价为：

$\{\begin{array}{l}{x}_2\frac{\partial \phi }{\partial x_1}-{\omega }^2{x}_1\frac{\partial \phi }{\partial x_2}=0\\ \left[2\alpha x_2+{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2+4{\alpha }^2{x}_2\pi k_1\right]+\frac{1}{2}\left(8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right)\frac{\partial \phi }{\partial x_2}=0\end{array}$ (16)

化简可得到：

$\frac{\text{d}\phi }{\text{d}\lambda }=\frac{2\alpha +{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)+4{\alpha }^2\pi k_1}{4{\alpha }^2{x}_2^2\pi k_1+{\omega }^4{x}_1^2\pi k_2+\pi k_3}$ (17)

若取 $4{\alpha }^2{k}_1=k_2{\omega }^2,{\beta }_1=\frac{\left(2\alpha +4{\alpha }^2\pi k_1\right){\omega }^4{k}_2}{k_3}$ 则：

$\begin{array}{c}\frac{\text{d}\phi }{\text{d}\lambda }=\frac{2\alpha +{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)+4{\alpha }^2\pi k_1}{\pi k_2{\omega }^2{x}_2^2+{\omega }^4{x}_1^2\pi k_2+\pi k_3}\\ =\frac{\left(2\alpha +4{\alpha }^2\pi k_1\right)\left[1+\frac{{\omega }^4{k}_2}{k_3}\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)\right]}{\pi k_3\left[1+\frac{{\omega }^4{k}_2}{k_3}\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)\right]}\\ =\frac{2\alpha +4{\alpha }^2\pi k_1}{\pi k_3}\end{array}$ (18)

故在广义平稳条件下，可解得该系统FPK方程的精确解为：

$p_e\left(x\right)=CExp\left[-\frac{2\alpha +4{\alpha }^2\pi k_1}{\pi k_3}\left(\frac{1}{2}{\omega }^2{x}_1^2+\frac{1}{2}{x}_2^2\right)\right]$ (19)

下面采用本文提出的数值解法求(12)的近似解，并将该近似解和上式精确解进行对比。首先，假设该系统的平稳转移概率密度函数为：

$p_n\left(x\right)=C\exp \left[a_{11}{x}_1+a_{12}{x}_2+a_{21}{x}_1^2+a_{22}{x}_1{x}_2+a_{23}{x}_2^2+\cdots +a_{ij}{x}_1^{i-j+1}{x}_2^{j-1}+\cdots +a_{nn+1}{x}_2^n\right]$ (20)

将式(20)带入FPK方程(12)中，固定住n，就有

$\begin{array}{l}\frac{\partial x_2{p}_n}{\partial x_1}+\frac{\partial \left[-2\alpha x_2-{\omega }^2{x}_1-{\beta }_1\left(x_1^2+\frac{x_2^2}{{\omega }^2}\right)x_2+4{\alpha }^2{x}_2\pi k_1\right]p_n}{\partial x_2}\\ -\frac{1}{2}\frac{{\partial }^2\left[8{\alpha }^2{x}_2^2\pi k_1+2{\omega }^4{x}_1^2\pi k_2+2\pi k_3\right]p_n}{\partial x_2^2}=0\end{array}$ (21)

运用待定系数法确定p_n的系数，我们可求得此近似解。当取 $\omega =\text{1}$, $k_1=k_2=k_3=1$ 时，求得 $\alpha =0.\text{5}$, ${\beta }_1=0.28$。

当取n = 2时，我们使用Mathematica解得：

$a_{11}=a_{12}=a_{22}=0;a_{21}=-0.579577;a_{23}=-0.579577;$ (22)

此时

$p_2\left(x\right)=-0.579577x_1^2-0.579577x_2^2$ (23)

当取n = 6时，我们解得：

$\begin{array}{l}{a}_{11}=a_{12}=a_{22}=a_{31}=a_{32}=a_{33}=a_{34}=a_{42}=a_{44}=a_{51}=a_{52}=a_{53}=a_{54}=a_{55}\\ =a_{56}=a_{62}=a_{64}=a_{66}=0;a_{21}=-0.579577;a_{23}=-0.579577;\\ a_{41}=0.000126739;a_{43}=0.000253479;a_{45}=0.000126739;\\ a_{61}=-0.0000844929;a_{63}=-0.000253479;a_{65}=-0.000253479;\\ a_{67}=-\mathrm{0.0000844929.}\end{array}$ (24)

此时：

$\begin{array}{c}{p}_6\left(x\right)=-0.579577x_1^2+0.000126739x_1^4-0.0000844929x_1^6-0.579577x_2^2\\ +0.000253479x_1^2{x}_2^2-0.000253479x_1^4{x}_2^2+0.000126739x_2^4\\ -0.000253479x_1^2{x}_2^4-0.0000844929x_2^6\end{array}$ (25)

数值模拟结果如图1：

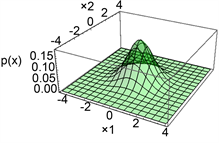(a) p₂(x)示意图 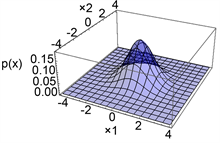(b) p₆(x)示意图 (c) p_e(x)示意图

Figure 1. Schematic diagram of steady-state transfer probability density function

图1. 稳态转移概率密度函数示意图

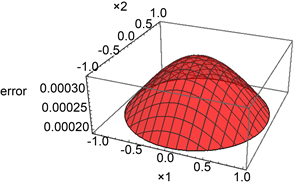
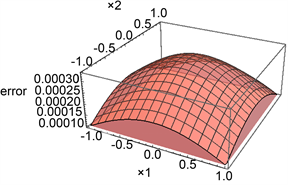
下面我们重点比较两种解的误差情况。图2展示了在不同区域，近似解和精确解的误差图，通过比较，我们发现误差基本在0.0003之内，精度较高。从图1中我们也可以看到，系统的状态变量主要集中在(−2, 2)之间，因此，图3展示了在此区域内，不同小范围的精确度。图中不同颜色的线表示不同的区域，对应不同的精确度。总体来看，该方法在稳态区域的精确度非常高。

(a) $x_1^2+x_2^2\le 1$ (b) $\left|x_1\right|\le 1;\left|x_2\right|\le 1$

Figure 2. The error graph of p₆(x) and p_e(x)

图2. p₆(x)和p_e(x)误差图

Figure 3. Accuracy diagram of steady state region

图3. 稳态区域的精确度示意图

表1和表2分别给出平衡态附近的不同区域内，近似解以及精确解的取值和误差比较，观察这些数据我们可以看出，两种解的误差非常微弱，这也说明我们的方法较精确。

Table 1. List of values for numerical and exact solutions near equilibrium

表1. 平衡态附近，数值解与精确解取值一览表

Table 2. List of errors for numerical and exact solutions near equilibrium

表2. 平衡态附近，数值解与精确解误差一览表

3.2. 例2

考虑：

$\ddot{X}+\left[a+{\left(bX+c\stackrel{\dot{}}{X}\right)}^2\right]\stackrel{\dot{}}{X}+X=\left(dX+e\stackrel{\dot{}}{X}\right)W_1\left(t\right)+W_2\left(t\right)$ (26)

式中 $a,b,c,d,e$ 是常数， $W_1\left(t\right),W_2\left(t\right)$ 是功率谱密度常数分别为 $k_1,k_2$ 的独立高斯白噪声。假设 $X_1=X,X_2=\stackrel{\dot{}}{X}$，可以得到该系统的Stratonovich型随机微分方程为：

$\{\begin{array}{l}\text{d}{X}_1=X_2\text{d}t\\ \text{d}{X}_2=\left\{-\left[a+{\left(b{X}_1+c{X}_2\right)}^2\right]X_2-X_1\right\}\text{d}t+\left(d{X}_1+e{X}_2\right)\sqrt{2\pi k_1}\circ \text{d}{B}_1\left(t\right)+\sqrt{2\pi k_2}\circ \text{d}{B}_2\left(t\right)\end{array}$ (27)

式中 $B_1\left(t\right),B_2\left(t\right)$ 为单位维纳过程。转化为Itô型随机微分方程：

$\{\begin{array}{l}\text{d}{X}_1=X_2\text{d}t\\ \text{d}{X}_2=\left\{-\left[a+{\left(b{X}_1+c{X}_2\right)}^2\right]X_2-X_1+\pi k_{1}e\left(d{X}_1+e{X}_2\right)\right\}\text{d}t+\left(d{X}_1+e{X}_2\right)\sqrt{2\pi k_1}\text{d}{B}_1\left(t\right)+\sqrt{2\pi k_2}\text{d}{B}_2\left(t\right)\end{array}$ (28)

式中 $\pi k_{1}e\left(d{X}_1+e{X}_2\right)$ 是 Wong-Zakai修正项。从而我们可以得到系统的FPK方程为：

$\begin{array}{l}\frac{\partial X_{2}p}{\partial X_1}+\frac{\partial \left\{-\left[a+{\left(b{X}_1+c{X}_2\right)}^2\right]X_2-X_1+\pi k_{1}e\left(d{X}_1+e{X}_2\right)\right\}p}{\partial x_2}\\ -\frac{{\partial }^2\left[{\left(d{X}_1+e{X}_2\right)}^2\pi k_1+\pi k_2\right]p}{\partial X_2^2}=0\end{array}$ (29)

如之前的计算过程类似，我们假设系统(26)的平稳转移概率密度函数为：

$p_n\left(X\right)=C\exp \left[a_{11}{X}_1+a_{12}{X}_2+a_{21}{X}_1^2+a_{22}{X}_1{X}_2+a_{23}{X}_2^2+\cdots +a_{ij}{X}_1^{i-j+1}{X}_2^{j-1}+\cdots +a_{nn+1}{X}_2^n\right]$ (30)

C归一化常数。把该近似解带入(29)中，可以得到：

$\frac{\partial X_2{p}_n}{\partial X_1}+\frac{\partial \left\{-\left[a+{\left(b{X}_1+c{X}_2\right)}^2\right]X_2-X_1+\pi k_{1}e\left(d{X}_1+e{X}_2\right)\right\}{p}_n}{\partial X_2}-\frac{{\partial }^2\left[{\left(d{X}_1+e{X}_2\right)}^2\pi k_1+\pi k_2\right]p_n}{\partial X_2^2}=0$ (31)

若取 $a=4;b=\frac{5}{4};c=-\frac{15}{4};d=\frac{1}{2};e=-\frac{3}{2};k_1=k_2=\frac{1}{\pi }$。我们首先使用本文提出的数值解法求得平稳转移概率密度函数的系数，得到FPK方程的近似解为：

$p_n\left(X\right)=\frac{25}{16\pi }{\text{e}}^{-\frac{25}{32}\left(X_1^2+4X_2^2\right)}$ (32)

图4给出了p_n的数值模拟示意图。

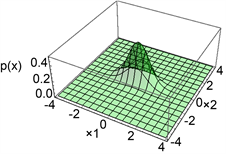(a) p₂(x)示意图 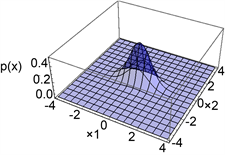(b) p₄(x)示意图 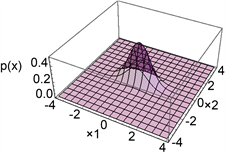(c) p₆(x)示意图

Figure 4. Schematic diagram of steady-state transfer probability density function

图4. 稳态转移概率密度函数示意图

下面我们采用 Milsteins 离散方法，得到(28)的离散化形式：

$\{\begin{array}{l}{X}_1\left(t_{j+1}\right)=X_1\left(t_j\right)+X_2\left(t_j\right)\Delta t\\ X_2\left(t_{j+1}\right)=X_2\left(t_j\right)+\left\{-\left[a+{\left(b{X}_1\left(t_j\right)+c{X}_2\left(t_j\right)\right)}^2\right]X_2\left(t_j\right)-X_1\left(t_j\right)+\pi k_{1}e\left(d{X}_1\left(t_j\right)+e{X}_2\left(t_j\right)\right)\right\}\Delta t\\ +\left(d{X}_1\left(t_j\right)+e{X}_2\left(t_j\right)\right)\sqrt{2\pi k_1}\Delta W_1\left(t\right)+\sqrt{2\pi k_2}\Delta W_2\left(t\right)\\ +\frac{1}{2}\left\{\left[d\left(d{X}_1\left(t_j\right)+e{X}_2\left(t_j\right)\right)2\pi k_1\right]\left(\Delta W_1{\left(t\right)}^2-\Delta t\right)+\left[e\left(d{X}_1\left(t_j\right)+e{X}_2\left(t_j\right)\right)2\pi k_1\right]\left(\Delta W_2{\left(t\right)}^2-\Delta t\right)\right\}\end{array}$ (33)

其中 $\Delta W_1\left(t\right),\Delta W_2\left(t\right)$ 服从 $N\left(0,\Delta t\right)$。模拟结果如图5所示：

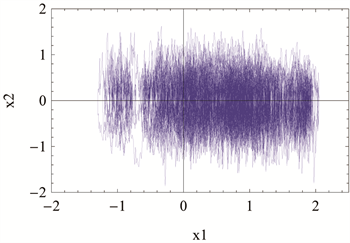
Figure 5. Phase diagram of system (28)

图5. 系统(28)的相图示意图

长时间观察之后，我们发现系统的状态变量X₁集中出现在(−1.2, 2)之间，X₂集中出现在(−1.5, 1.8)之间。我们令(32)对X₁和X₂分别在区间(−1.2, 2)和(−1.5, 1.8)上积分，得其值为0.93。换句话说，根据本文提出的近似算法，我们估计此系统的状态变量X₁和X₂分别出现在区间(−1.2, 2)和(−1.5, 1.8)上的概率为0.93。可以看出此结果与图5所示结果具有很高的一致性。

3.3. 结论

本篇论文主要解决了一类非线性随机微分动力系统转移概率密度函数的求解及其有效性问题。首先我们提出一种近似方法，即假设系统FPK方程的解为指数多项式的形式，运用待定系数法求出多项式的系数，然后就可得到FPK方程的近似解。接着，通过两个具体的案例，我们详细地阐述了求解过程。通过比较广义平稳条件下得出的精确解和该近似解的误差，以及比较用近似解求出的状态变量位于稳态区域的概率和系统离散化后相图展示的结果，我们发现该方法不仅计算简便，而且精度很高，是求解转移概率密度函数的一种有效方法。在求解一般的FPK方程时，本文提出的模拟思路读者可以直接套用。

基金项目

中国自然科学基金(11501410；51573133；11672207)，天津市自然科学基金(17JCQNJC03800；17JCYBJC15700)。

NOTES

^*通讯作者。