1. 引言
近几十年以来,非线性动力系统的研究获得了很大的发展。学者们对动力系统的平衡点稳定性、分叉、混沌等性质进行了深入的研究,并发展出了超混沌、混沌吸引子、隐藏吸引子、多稳态等新的概念 [1] - [6]。
在人们所研究的动力系统中,平衡点的数量和分叉的类型也不尽相同。经典的Lorenz族系统 [7] [8] [9] [10] [11] 和Rössler系统 [12] [13] 有着有限个平衡点。Wei研究了没有平衡点但存在隐藏超混沌吸引子的系统 [14];Jafari和Sprott所研究的系统具有线平衡点,同样可以产生混沌吸引子 [15];另外在一些文章中,系统具有无穷多个平衡点,但是吸引子的数量却是有限的 [16]。本文基于Moffatt [17] 提出的分段盘式发电机系统构造了一个新的四维系统,它可以有任意给定数量的平衡点:在没有平衡点或有线平衡点的情形下可以存在隐藏混沌吸引子;在具有有限个平衡点的情形下可以存在超混沌吸引子;在具有无穷多个平衡点的情形下可以存在无穷多个混沌吸引子。这项工作综合地说明了具有各种数量平衡点的动力系统都可以存在混沌吸引子,并且创新性地找到了具有无穷多个混沌吸引子的系统。此外,新系统在某些参数条件下可以使得两个平衡点同时发生Hopf分叉并产生两个有一定对称性的极限环。希望这项工作能为非线性动力系统的研究做出一定的贡献。
本文组织如下。第2节基于分段盘式发电机模型引入了新的四维超混沌系统,研究了它在不同参数条件下可以拥有任意给定数量平衡点的特性,并且给出了部分参数条件下平衡点的稳定条件。第3节研究了新系统的混沌特性,利用数值模拟的方法说明了拥有各个数量平衡点的系统都具有混沌/超混沌的性质。第4节研究了新系统的分叉性质,通过理论证明了系统在某些参数条件下拥有两个平衡点,它们会同时经历Hopf分叉产生极限环,并用数值模拟加以佐证。最后一节对全文进行了总结并简要给出了一些发展性的评论。
2. 新的四维超混沌系统
2.1. 系统形式
Moffatt [18] 提出了一种分段盘式发电机模型如下:
基于上述系统,我们构造了一个如下带有两个三角函数项的四维系统
(1)
记系统(1)的参数组为
。在本文中令
,其中
可以算出系统(1)的散度为
因此系统(1)是耗散的。
令
,此时系统(1)没有平衡点。选取初始条件为
,则得到系统(1)有一个隐藏超混沌吸引子,四个李雅普诺夫指数为
李雅普诺夫维数为
。图1展示了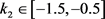 时的李雅普诺夫指数谱。
时的李雅普诺夫指数谱。

Figure 1. Parameters
, the initial condition is
,
Lyapunov exponent spectrum of system (1)
图1. 参数
,初始条件为
,
时系统(1)的李雅普诺夫指数谱
2.2. 平衡点的数量
本小节研究系统(1)平衡点的数量。
定理1 设
,则系统(1)可以有任意给定数量的平衡点,具体可以罗列为如下的性质:
(I)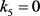 的情形
的情形
(1) 令
并且
,则
(a) 如果
,则系统(1)没有平衡点;
(b) 如果
,则系统(1)有一条线平衡点
(c) 如果
,则系统(1)有两个平衡点
其中
(2) 令
,
并且
,则系统(1)有无穷多个孤立平衡点,具体如下:
(a) 如果
,则系统(1)的平衡点为
(b) 如果
,则系统(1)的平衡点为
其中
(3) 令
并且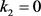 ,则
,则
(a) 如果
,则系统(1)没有平衡点;
(b) 如果
,则系统(1)有一条线平衡点
(c) 如果
,则系统(1)有
个平衡点,其中N可以是任意预先给定非负整数。
(4) 令
并且
,则系统(1)有2N个平衡点,其中N可以是任意预先给定非负整数。
(II)
并且
的情形
(1) 令
,
并且
,则系统(1)有唯一平衡点
(2) 令
,
并且
,则系统(1)有无穷多个孤立平衡点
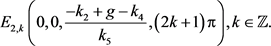
(3) 令
,
并且
,则系统(1)可以有任意给定奇数个平衡点。
证明 假设
是系统(1)的一个平衡点。由
可以得到
,因此
可以记为
。此外,我们有
(2)
(I)
的情形
(1) 当
并且
时,由
可得
。于是
因此,
(a) 如果
,则系统(1)没有平衡点;
(b) 如果
,由
可得
,这直接可以推得
。因此
;
(c) 如果
,由
可得
而由于
以及
,
必须取1。
(2) 当
,
并且
时,由
可得
,因此
。很显然,
考虑到
,有
也就是说,
,因此
。于是
,其中
由于
以及
,
必须为1。因此,
(a) 如果
,则系统(1)的平衡点为
(b) 如果
,则系统(1)的平衡点为
(3) 当
并且
时,有
如果
,则系统(1)没有平衡点。若
,则有
,再结合
可以得到
以及
。
现在考虑
的情形。由
可得
该方程关于
有
个解
,其中
。于是系统(1)可以有
个平衡点
其中,
(4) 当
并且
时,仍设关于
的方程
有
个解
,
并且
。图2显示了当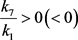 时曲线
和直线
在
(四)
时曲线
和直线
在
(四)
象限的交点。
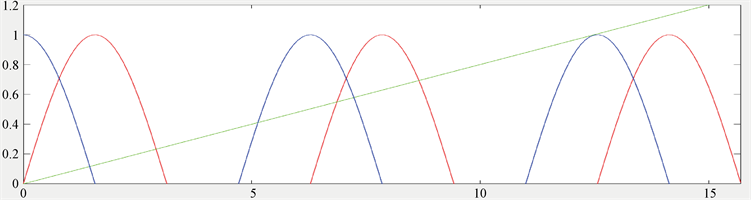
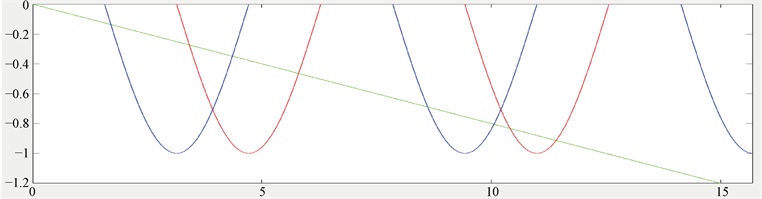
Figure 2. The intersection of curve
and straight line
图2. 曲线 和直线
的交点
和直线
的交点
可以看出,
,
并且
,即
对这些解做一个重排
则有
考虑
定义一个函数
。结合
可知
因此,
(a) 如果
,则系统(1)没有平衡点;
(b) 如果存在
,使得
,则系统(1)有4i个平衡点
其中
(c) 如果
,则系统(1)有
个平衡点
及
其中
(II)
并且
的情形
(1) 当
,
并且
,可以得到
以及
。假设
,则
并且有
因此,
必须为0。所以系统(1)只有唯一平衡点
(2) 当
,
并且
时,可以得到
,于是
。由
和
可得
。同样地,若假设
则有
,并有
因此
同样必须为0。此时系统(1)有无穷多个孤立平衡点
(3) 当
,
并且
时,仍设
的解为
。对于
可以得到一个平衡点
而对于
,由
可得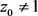 以及
。将此式代入
可得
以及
。将此式代入
可得
作变换
可得
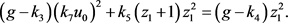 (3)
(3)
即
(4)
由于
,
以及
,关于
的一元三次方程(4)的判别式
于是对于每一个给定的
,方程(4)都有唯一解,进而关于
的方程(4)亦有唯一解。因此,系统(1)有
个平衡点
其中,
是下列关于
的方程的唯一解:
2.3. 稳定性
本小节分析系统(1)在部分参数条件下平衡点的稳定性。
系统(1)的雅可比矩阵为
这里先给出三个下文常用的量的定义
(5)
其中
是正在讨论稳定性的平衡点的第一个分量。
(I)
的情形
(1) 当
,
并且
时,
的特征多项式都为
根据Routh-Hurwitz判据,
稳定当且仅当
即
(2) 当
,
并且
,
的特征方程皆为
根据Routh-Hurwitz判据,
稳定当且仅当
即
(II)
并且
的情形
(1) 当
,
并且
时,
的特征多项式为
根据Routh-Hurwitz判据,
稳定当且仅当
由于
,等价条件可以简化为
(2) 当
,
并且
,
和
的特征多项式表示为
由此,特征根分别为
,
以及
由
可得
,于是
。又由
可知,如果
,则
稳定而
不稳定;否则
不稳定而
稳定。
3. 混沌性质
3.1. 没有平衡点的混沌系统
令
,此时系统(1)没有平衡点。选取初始点为
可得系统(1)是混沌的,四个李雅普诺夫指数为
李雅普诺夫维数为
。数值模拟证实了系统(1)确实有一个隐藏混沌吸引子,如图3所示。
3.2. 具有有限个平衡点的超混沌/混沌系统
3.2.1. 具有两个平衡点的超混沌系统
令
,此时系统(1)有两个非双曲平衡点
选取初始点为
可得系统(1)是超混沌的,四个李雅普诺夫指数为
李雅普诺夫维数为
。数值模拟证实了系统(1)确实有一个超混沌吸引子,如图4所示。

Figure 3. The parameter group is
, when the initial condition is selected as
, the system (1 ) x-y-z space phase diagram (left picture) and Poincaré mapping on xz plane (right picture)
图3. 参数组为
,选取初始条件为
时,系统(1)的x-y-z空间相图(左图)和x-z平面上的庞加莱映射(右图)
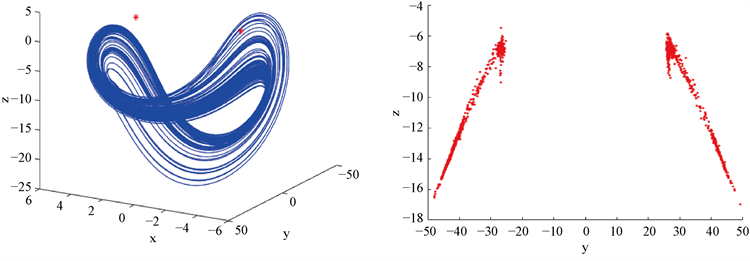
Figure 4. When the parameter group is
, when the initial conditions are selected as
, the system (1) the x-y-z space phase diagram (left picture) and the Poincaré map on the yz plane (right picture)
图4. 参数组为
,选取初始条件为
时,系统(1)的x-y-z空间相图(左图)和y-z平面上的庞加莱映射(右图)
3.2.2. 具有六个平衡点的混沌系统
令
,此时系统(1)有六个不稳定的平衡点
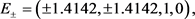
选取初始点为
可得系统(1)是混沌的,四个李雅普诺夫指数为
李雅普诺夫维数为
。数值模拟证实了系统(1)确实有一个混沌吸引子,如图5所示。

Figure 5. When the parameter group is
, when the initial conditions are selected as
the system (1) x-y-z space phase diagram (left picture) and Poincaré mapping on x-z plane (right picture)
图5. 参数组为
,选取初始条件为
时,系统(1)的x-y-z空间相图(左图)和x-z平面上的庞加莱映射(右图)
3.3. 具有无穷多个平衡点的混沌系统
3.3.1. 具有无穷多个孤立平衡点的混沌系统
令
,此时系统(1)有无穷多个不稳定的孤立平衡点
选取初始点为
可得系统(1)是混沌的,四个李雅普诺夫指数为
李雅普诺夫维数为
。数值模拟证实了系统(1)确实有无穷多个混沌吸引子,如图6所示。
3.3.2. 具有一条线平衡点的混沌系统
令
,此时系统(1)有一条直线平衡点
选取初始点为
可得系统(1)是混沌的,四个李雅普诺夫指数为
李雅普诺夫维数为
。数值模拟证实了系统(1)确实有一个隐藏混沌吸引子,如图7所示。
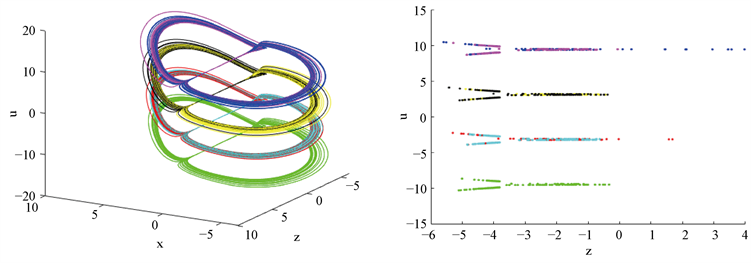
Figure 6. When the parameter group is
and the initial condition is selected as
, the system (1) the x-y-u space phase diagram (left picture) and the Poincaré map on the z-u plane (right picture)
图6. 参数组为
,选取初始条件为
时,系统(1)的x-y-u空间相图(左图)和z-u平面上的庞加莱映射(右图)
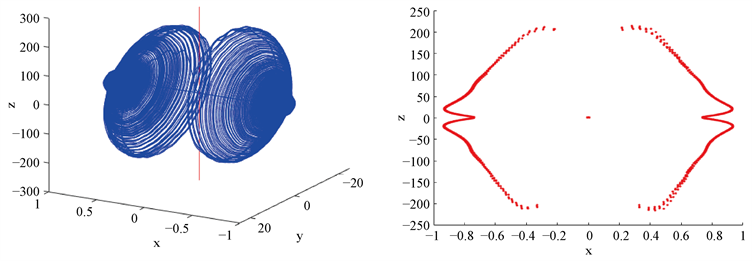
Figure 7. The parameter group is
, when the initial condition is selected as
, the system (1) x-y-z space phase diagram (left picture) and Poincaré mapping on x-z plane (right picture)
图7. 参数组为
,选取初始条件为
时,系统(1)的x-y-z空间相图(左图)和x-z平面上的庞加莱映射 (右图)
4. Hopf分叉
4.1. Hopf分叉的存在性和周期轨的稳定性
当
,
并且
时,系统(1)有两个平衡点
,其中
。
定理2 令
其中
当
时,系统(1)有两个平衡点
,并且它们都在
处经历了Hopf分叉。
证明 设
。首先有
以及
于是
所以系统(1)有两个平衡点
,其中
。
的特征方程为
(6)
其中
。
为了证明
有一对共轭纯虚根,将
代入
可以得到需要满足的条件为
(7)
以及
其中第一个不等式条件显然成立,而第二个条件等价为
即
由于
,这个条件也是成立的。
接着我们来证明
的另外两个根都是负实根。根据
有着共轭虚根
,
可以做如下分解
(8)
对照式(6)和式(8)的系数可得,
(9)
并且
于是有
(10)
因此,
的根为
以及
。
最后,我们考虑横截性条件。将
关于
进行求导得
令
并且观察到式(7),于是
由此,
即
(11)
定理3 当参数组
时,平衡点
的第一李雅普诺夫系数皆由下式给出
其中
(I) 如果
,则系统(1)将同时在平衡点
处发生Hopf分叉,并且在
附近产生的两个分叉周期轨道在
时是稳定的,在
时是不稳定的。
证明 记
为系统(1)的一个平衡点(X可取
)。于是
(12)
作变换
并且令
,则系统(1)变换为了如下系统(变量仍记为
):
此时平衡点
被平移到了原点
。
根据式(11),横截性条件是满足的。现在来计算第一李雅普诺夫系数,它可以表明平衡点和出现的周期轨的稳定性。当参数组
时,平衡点的特征根为
和
,其中E和
可以由式(9)和式(10)计算得出。依据 [18],
其中
接着可以计算出下列值:
其中
从而
其中
注意到式(12),则可得到最终结果
4.2. 数值模拟
本小节对4.1小节所证明的Hopf分支进行数值模拟。
取参数
根据定理2,
。当
时,选取初始条件
,得到了两个不稳定的极限环,如图8所示。
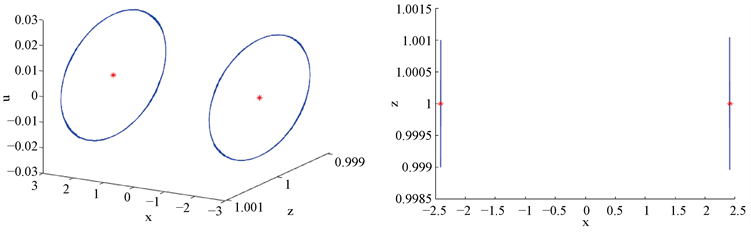
Figure 8. The parameter group is
select initial conditions
, system (1) there are two unstable limit cycles
图8. 参数组为
,选取初始条件
,系统(1)存在两个不稳定的极限环
5. 总结
本文构造了一个可以具有任意预先给定数目平衡点的四维ODE系统。通过数值方法计算李亚普诺夫指数,本文揭示了新系统在不同参数下的许多混沌特性:(i) 没有平衡点的系统存在隐藏混沌吸引子;(ii) 具有两个非双曲平衡点的系统存在超混沌吸引子;(iii) 具有六个不稳定平衡点的系统存在混沌吸引子;(iv) 具有无穷多个不稳定孤立平衡点的系统存在无穷多个混沌吸引子;(v) 具有线平衡点的系统存在混沌吸引子。通过理论证明和数值模拟,证明了新系统在一定参数条件下具有两个平衡点,并且两个平衡点同时经历Hopf分岔,并产生两个具有一定对称性的极限环。
虽然数值计算表明,具有任意数目平衡点的ODE系统都可以具有混沌特性,但是平衡点的数目和稳定性与混沌特性之间的关系仍然是一个困难的问题。此外,多个平衡点在相同参数下同时发生分岔也是一个值得研究的有趣现象。