quasi-h-Bernstein-Vandermonde矩阵的特征值的高精度计算

Accurate Computations for Eigenvalues of quasi-h-Bernstein-Vandermonde Matrix

摘要: 在本文中，我们首先提供了quasi-h-Bernstein-Vandermonde矩阵的重新参数化，并高精度计算出所有的参数。然后得出了计算此类矩阵的所有特征值的高精度算法。最后给出数值实验来验证所提出算法的高精度性。

Abstract: In this paper, we first provide a re-parametrization of the class of quasi-h-Bernstein-Vandermonde matrix and the parameters are calculated with high relative accuracy. Then, we present new algo-rithms for computing all the eigenvalues of such matrix to high relative accuracy. Finally, numerical experiment is given to confirm the high relative accuracy of our algorithms.

1. 引言

若一个矩阵的所有子式都是非正的(非负的)，则称此矩阵为完全非正(非负)矩阵。若矩阵A的所有k阶非零子式有相同符号 ${\epsilon }_k\left(k=1,\cdots ,n\right)$，则称矩阵A为符号序列为 $\left\{{\epsilon }_k\right\}\left({\epsilon }_k=\pm 1\right)$ 的符号规则矩阵(简称为SR矩阵)。这几类结构矩阵在概率论、组合学和数值代数等中都有着广泛的应用 [1] [2] [3]。

在数值线性代数中，我们追求的目标是高精度的数值计算。在文 [4] 中，R. Huang对两类特殊的符号序列为 $\left(1,\cdots ,1,-1\right)$ 的广义SR矩阵(quasi-Vandermonde and quasi-Cauchy)的所有特征值进行了高精度计算。

本文将研究quasi-h-Bernstein-Vandermonde矩阵 $A=\left(a_{ij}\right)\in {ℝ}^{n\times n}$ 的所有特征值的高精度计算，此类矩阵的形式如下：

$a_{ij}=\{\begin{array}{l}\frac{\left(\begin{array}{c}n-1\\ j-1\end{array}\right)\underset{k=0}{\overset{j-2}{{\displaystyle \prod }}}\left(t_i+kh\right)\underset{k=0}{\overset{n-j-1}{{\displaystyle \prod }}}\left(1-t_i+kh\right)}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)},\left(i,j\right)\ne \left(n,n\right);\\ \frac{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(t_n+kh\right)}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)}-z,\left(i,j\right)=\left(n,n\right),\end{array}$ (1.1)

其中 $h\ge 0$， $0<t_1<t_2<\cdots <t_n<1$， $\frac{\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)}{\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_l\right)}<z\le t_n\frac{\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)}{\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_l\right)}$。

在文 [5] 定理9中，符号序列为 $\left(1,\cdots ,1,-1\right)$ 的非奇异SR矩阵 $A\in {ℝ}^{n\times n}$ 被唯一分解为

$A=B_1\cdots B_{n-2}{B}_{n-1}P{B}_{n}D{C}_{n-1}\cdots C_1$ (1.2)

且

$\{\begin{array}{l}{d}_{ii}>0,1\le i\le n;\\ {\beta }_{ij}\ge 0,1\le j<i\le n;\\ {\alpha }_{ij}\ge 0,1\le i<j\le n,\end{array}$ (1.3)

满足

$\{\begin{array}{l}{\beta }_{21}>0,\cdots ,{\beta }_{n-1,n-2}>0;{\beta }_{ij}=0\Rightarrow {\beta }_{kj}=0,\forall k>i,\\ {\alpha }_{12}>0,\cdots ,{\alpha }_{n-2,n-1}>0;{\alpha }_{ij}=0\Rightarrow {\alpha }_{ir}=0,\forall r>j,\end{array}$ (1.4)

其中 $P=diag\left(I_{n-2},-P_2\right)\in {ℝ}^{n\times n}$， $I_n\in R^{n\times n}$ 和 $P_n\in R^{n\times n}$ 分别是单位矩阵和反单位矩阵， $D=diag\left(d_{ii}\right)\in {ℝ}^{n\times n}$， $B_i\in {ℝ}^{n\times n}\left(1\le i\le n-2\right)$， $B_{n-1}$， $B_n$ 和 $C_i\in {ℝ}^{n\times n}\left(1\le i\le n-1\right)$ 是双对角矩阵，如下：

$B_i=\left[\begin{array}{ccccccc}1& & & & & & \\ 0& 1& & & & & \\ & \ddots & \ddots & & & & \\ & & 0& 1& & & \\ & & & {\beta }_{n-i+1,1}& 1& & \\ & & & & \ddots & \ddots & \\ & & & & & {\beta }_{n,i}& 1\end{array}\right]$， $C_i=\left[\begin{array}{ccccccc}1& 0& & & & & \\ & \ddots & \ddots & & & & \\ & & 1& 0& & & \\ & & & 1& {\alpha }_{1,n-i+1}& & \\ & & & & \ddots & \ddots & \\ & & & & & 1& {\alpha }_{i,n}\\ & & & & & & 1\end{array}\right]$ (1.5)

$B_{n-1}=\left[\begin{array}{ccccc}1& & & & \\ {\beta }_{21}& 1& & & \\ & \ddots & \ddots & & \\ & & {\beta }_{n-1,n-2}& 1& \\ & & & 0& 1\end{array}\right]$， $B_n=\left[\begin{array}{ccccc}1& & & & \\ 0& 1& & & \\ & \ddots & \ddots & & \\ & & 0& 1& \\ & & & {\beta }_{n,n-1}& 1\end{array}\right]$.(1.6)

在文 [4] 中，符号序列为 $\left(1,\cdots ,1,-1\right)$ 的SR矩阵 $A\in {ℝ}^{n\times n}$ ( $n>2$ )被除(1.3)中的 ${\alpha }_{n-1,n}$ 和 $\delta$ 以外的非平凡元素参数化，所有参数被存储在形如矩阵 $PM\left(A\right)$ 中，且

$PM{\left(A\right)}_{ij}=\{\begin{array}{l}{d}_{ii}>0,1\le i\le n;\\ {\beta }_{ij}\ge 0,1\le j<i\le n;\\ {\alpha }_{ij}\ge 0,1\le i<j\le n,\left(i,j\right)\ne \left(n-1,n\right);\\ \delta ,\left(i,j\right)=\left(n-1,n\right);\end{array}$ (1.7)

满足

$PM{\left(A\right)}_{ii}>0,\forall 1\le i\le n;PM{\left(A\right)}_{i+1,i}>0,PM{\left(A\right)}_{i,i+1}>0,\forall 1\le i\le n-2;$ (1.8)

参数矩阵 $PM\left(A\right)\in R^{n\times n}$ 的符号正则性如下：

$\{\begin{array}{l}sign\left(PM\left(A\right)\left(i,i\right)\right)=s_i,\forall 1\le i\le n,\\ sign\left(PM\left(A\right)\left(i,1:i-1\right)\right)=r_i,\forall 2\le i\le n,\\ sign\left(PM\left(A\right)\left(1:i-1,i\right)\right)=c_i,\forall 2\le i\le n,\\ s_{i-1}{s}_i=1,r_i{c}_i=1或0,\forall 2\le i\le n,\end{array}$ (1.9)

其中 $s_i,r_i,c_i=\pm 1或\text{0}$。因此， $sign\left(\alpha \right)=1$ 表示向量 $\alpha$ 的所有非零元素是正的， $sign\left(\alpha \right)=-1$ 表示向量 $\alpha$ 的所有非零元素是负的，特别地；若向量 $\alpha =0$，则 $sign\left(\alpha \right)=\text{0}$。

在本文中，我们定义：

$A=:PM\left(A\right)\in R^{n\times n}$

通过(1.2)由 $PM\left(A\right)$ 生成的矩阵。

定义1.1 [4] 若 $PM\left(A\right)$ 满足(1.9)且 $r_n,c_n=1或\text{0}$，则称矩阵 $A=:PM\left(A\right)\in R^{n\times n}$ 是符号序列为 $\left(1,\cdots ,1,-1\right)$ 的广义SR矩阵。

必须强调的是，计算参数(1.7)的公式如下：

$\{\begin{array}{l}{d}_{ii}=\frac{\det A\left[1,\cdots ,i|1,\cdots ,i\right]}{\det A\left[1,\cdots ,i-1|1,\cdots ,i-1\right]},\forall 1\le i\le n-2,\\ d_{n-1,n-1}=\frac{\det A\left[2,\cdots ,n|1,\cdots ,n-1\right]}{\det A\left[2,\cdots ,n-1|1,\cdots ,n-2\right]},d_{n,n}=-\det A/{\displaystyle \underset{i=2}{\overset{n-1}{\prod }}{d}_{ii}},\\ {\beta }_{i,j}=\frac{\det A\left[i-j+1,\cdots ,i|1,\cdots ,j\right]}{\det A\left[i-j+1,\cdots ,i-1|1,\cdots ,j-1\right]}\cdot \frac{\det A\left[i-j,\cdots ,i-2|1,\cdots ,j-1\right]}{\det A\left[i-j,\cdots ,i-1|1,\cdots ,j\right]},\forall i>j\ne n-1,\\ {\beta }_{n,n-1}=\frac{\det A\left[1,\cdots ,n-1\right]}{\det A\left[1,\cdots ,n-2\right]}\cdot \frac{\det A\left[2,\cdots ,n-1|1,\cdots ,n-2\right]}{\det A\left[2,\cdots ,n|1,\cdots ,n-1\right]},\\ {\alpha }_{i,j}=\frac{\det A\left[1,\cdots ,i|j-i+1,\cdots ,j\right]}{\det A\left[1,\cdots ,i-1|j-i+1,\cdots ,j-1\right]}\cdot \frac{\det A\left[1,\cdots ,i-1|j-i,\cdots ,j-2\right]}{\det A\left[1,\cdots ,i|j-i,\cdots ,j-1\right]},\forall j>i\ne n-1,\\ \delta =\frac{\det A\left[2,\cdots ,n\right]}{d_{n-1,n-1}{\displaystyle \underset{t=3}{\overset{n}{\prod }}{d}_{t-2,t-2}{\alpha }_{t-2,t-1}{\beta }_{t-1,t-2}}},\end{array}$ (1.10)

本文将作以下安排：第2节给出quasi-h-Bernstein-Vandermonde矩阵的双对角分解，并且高精度计算出这类矩阵的所有参数。第3节给出计算此类矩阵的所有特征值的高精度算法。第4节给出数值例子来说明所提出算法的高精度性。

2. quasi-h-Bernstein-Vandermonde矩阵的双对角分解

定义2.1 [6] 如果矩阵 $B\in {ℝ}^{\left(n+1\right)\times \left(n+1\right)}$ 有如下形式，

$\left[\begin{array}{cccc}\left(\begin{array}{c}n\\ 0\end{array}\right)\frac{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_1+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}& \left(\begin{array}{c}n\\ 1\end{array}\right)\frac{t_1\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1-t_1+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}& \cdots & \left(\begin{array}{c}n\\ n\end{array}\right)\frac{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(t_1+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}\\ \left(\begin{array}{c}n\\ 0\end{array}\right)\frac{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_2+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}& \left(\begin{array}{c}n\\ 1\end{array}\right)\frac{t_2\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1-t_2+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}& \cdots & \left(\begin{array}{c}n\\ n\end{array}\right)\frac{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(t_2+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}\\ ⋮& ⋮& \ddots & ⋮\\ \left(\begin{array}{c}n\\ 0\end{array}\right)\frac{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_{n+1}+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}& \left(\begin{array}{c}n\\ 1\end{array}\right)\frac{t_{n+1}\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1-t_{n+1}+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}& \cdots & \left(\begin{array}{c}n\\ n\end{array}\right)\frac{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(t_{n+1}+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)}\end{array}\right]$ (2.1)

那么B是h-Bernstein-Vandermonde矩阵，其中 $h\in ℝ$， $0<t_1<t_2<\cdots <t_n<t_{n+1}<1$。

引理2.2 [6] 令 $B\in {ℝ}^{\left(n+1\right)\times \left(n+1\right)}$ 是形如(2.1)的h-Bernstein-Vandermonde矩阵，则

$\begin{array}{l}\det B\left[i-j+1,\cdots ,i|1,\cdots ,j\right]\\ =\left(\begin{array}{c}n\\ 0\end{array}\right)\left(\begin{array}{c}n\\ 1\end{array}\right)\cdots \left(\begin{array}{c}n\\ j-1\end{array}\right)\cdot \frac{{\displaystyle \underset{j-i+1\le s<l\le i}{\prod }\left(t_l-t_s\right)}\underset{k=0}{\overset{n-j}{{\displaystyle \prod }}}\underset{l=i-j+1}{\overset{i}{{\displaystyle \prod }}}\left(1-t_l+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{n-j}{{\displaystyle \prod }}}\left(1+kh\right)}\end{array}$ (2.2)

$\begin{array}{l}\det B\left[1,\cdots ,j|i-j+1,\cdots ,i\right]\\ =\left(\begin{array}{c}n\\ i-j\end{array}\right)\left(\begin{array}{c}n\\ i-j+1\end{array}\right)\cdots \left(\begin{array}{c}n\\ i-1\end{array}\right)\cdot \frac{{\displaystyle \underset{1\le s<l\le j}{\prod }\left(t_l-t_s\right)}\underset{k=0}{\overset{n-j}{{\displaystyle \prod }}}\underset{l=1}{\overset{j}{{\displaystyle \prod }}}\left(1-t_l+kh\right)\underset{k=0}{\overset{i-j-1}{{\displaystyle \prod }}}\underset{l=1}{\overset{j}{{\displaystyle \prod }}}\left(t_l+kh\right)}{\underset{k=0}{\overset{n-1}{{\displaystyle \prod }}}\left(1+kh\right)\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{n-j}{{\displaystyle \prod }}}\left(1+kh\right)}\end{array}$ (2.3)

推论2.3令 $A\in R^{n\times n}$ 是形如(1.1)的quasi-h-Bernstein-Vandermonde矩阵，则关于矩阵A的子式有如下的结论：

$\begin{array}{l}\det A\left[i,\cdots ,i+j-1|1,\cdots ,j\right]\\ =\left(\begin{array}{c}n-1\\ 0\end{array}\right)\left(\begin{array}{c}n-1\\ 1\end{array}\right)\cdots \left(\begin{array}{c}n-1\\ j-1\end{array}\right)\cdot \frac{{\displaystyle \underset{i\le s<l\le i+j-1}{\prod }\left(t_l-t_s\right)}\underset{k=0}{\overset{n-j-1}{{\displaystyle \prod }}}\underset{l=i}{\overset{i+j-1}{{\displaystyle \prod }}}\left(1-t_l+kh\right)}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\underset{k=0}{\overset{n-3}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{n-j-1}{{\displaystyle \prod }}}\left(1+kh\right)}\end{array}$ (2.4)

$\begin{array}{l}\det A\left[1,\cdots ,j|i,\cdots ,i+j-1\right]\\ =\left(\begin{array}{c}n-1\\ i-1\end{array}\right)\left(\begin{array}{c}n-1\\ i-2\end{array}\right)\cdots \left(\begin{array}{c}n-1\\ i+j-2\end{array}\right)\cdot \frac{{\displaystyle \underset{1\le s<l\le j}{\prod }\left(t_l-t_s\right)\underset{k=0}{\overset{n-i-j}{{\displaystyle \prod }}}\underset{l=1}{\overset{j}{{\displaystyle \prod }}}}\left(1-t_l+kh\right)\underset{k=0}{\overset{i-2}{{\displaystyle \prod }}}\underset{l=1}{\overset{j}{{\displaystyle \prod }}}\left(t_l+kh\right)}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\underset{k=0}{\overset{n-3}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{n-j-1}{{\displaystyle \prod }}}\left(1+kh\right)}\end{array}$ (2.5)

证明 因为 $A=B-z{E}_{nn}$，其中B是h-Bernstein-Vandermonde矩阵，

$E_{nn}={\left[\begin{array}{cccc}0& 0& \cdots & 0\\ 0& 0& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right]}_{n\times n}$.

所以

$\begin{array}{l}\det A\left[i,\cdots ,i+j-1|1,\cdots ,j\right]\\ =\det \left(B-z{E}_{nn}\right)\left[i,\cdots ,i+j-1|1,\cdots ,j\right]\\ =\det B\left[i,\cdots ,i+j-1|1,\cdots ,j\right]\end{array}$

$\begin{array}{l}\det A\left[1,\cdots ,j|i,\cdots ,i+j-1\right]\\ =\det \left(B-z{E}_{nn}\right)\left[1,\cdots ,j|i,\cdots ,i+j-1\right]\\ =\det B\left[1,\cdots ,j|i,\cdots ,i+j-1\right]\end{array}$

由h-Bernstein-Vandermonde矩阵的子式的引理2.2，结论得证。

定理2.4 令 $A=\left(a_{ij}\right)\in {ℝ}^{n\times n}$ 是一个形如(1.1)的非奇异quasi-h-Bernstein-Vandermonde矩阵。则 $PM\left(A\right)\in R^{n\times n}$ 如下：

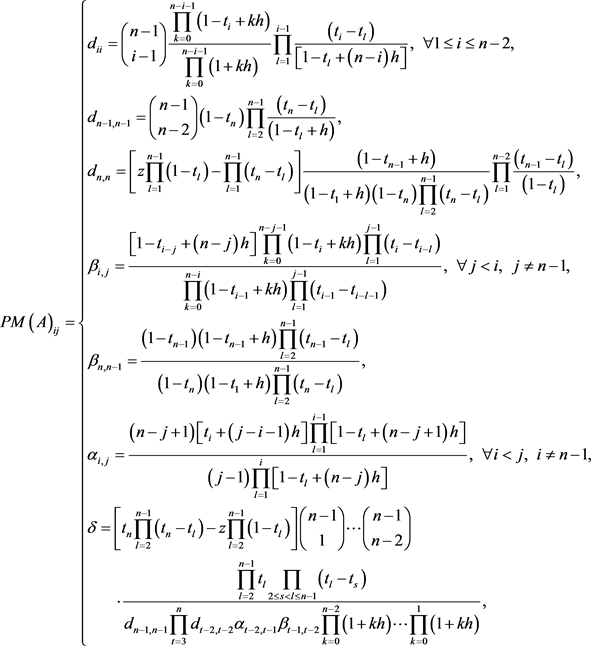(2.6)

证明 接下来，计算所有参数的表达式

① 利用推论2.3中的表达式(2.4)得到：

$\{\begin{array}{l}{\beta }_{i1}=\frac{\det A\left[i|1\right]}{\det A\left[i-1|1\right]}=\frac{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1-t_i+kh\right)}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1-t_{i-1}+kh\right)},\forall 1<i\le n;\\ {\beta }_{i,j}=\frac{\det A\left[i-j+1,\cdots ,i|1,\cdots ,j\right]}{\det A\left[i-j+1,\cdots ,i-1|1,\cdots ,j-1\right]}\cdot \frac{\det A\left[i-j,\cdots ,i-2|1,\cdots ,j-1\right]}{\det A\left[i-j,\cdots ,i-1|1,\cdots ,j\right]}\\ =\frac{\left[1-t_{i-j}+\left(n-j\right)h\right]\underset{k=0}{\overset{n-j-\text{1}}{{\displaystyle \prod }}}\left(1-t_i+kh\right)\underset{l=1}{\overset{j-1}{{\displaystyle \prod }}}\left(t_i-t_{i-l}\right)}{\underset{k=0}{\overset{n-j}{{\displaystyle \prod }}}\left(1-t_{i-1}+kh\right)\underset{l=1}{\overset{j-1}{{\displaystyle \prod }}}\left(t_{i-1}-t_{i-l-1}\right)},\forall \text{1}\le j\le n-2,j<i\le n.\end{array}$ (2.7)

② 利用推论2.3中的表达式(2.5)得到：

$\{\begin{array}{l}{\alpha }_{1j}=\frac{\det A\left[1|j\right]}{\det A\left[1|j-1\right]}=\frac{\left(n-j+1\right)\left[t_1+\left(j-2\right)h\right]}{\left(j-1\right)\left[1-t_1+\left(n-j\right)h\right]},\forall 1<j\le n;\\ {\alpha }_{i,j}=\frac{\det A\left[1,\cdots ,i|j-i+1,\cdots ,j\right]}{\det A\left[1,\cdots ,i-1|j-i+1,\cdots ,j-1\right]}\cdot \frac{\det A\left[1,\cdots ,i-1|j-i,\cdots ,j-2\right]}{\det A\left[1,\cdots ,i|j-i,\cdots ,j-1\right]}\\ =\frac{\left(n-j+1\right)\left[t_i+\left(j-i-1\right)h\right]\underset{l=1}{\overset{i-1}{{\displaystyle \prod }}}\left[1-t_l+\left(n-j+1\right)h\right]}{\left(j-1\right)\underset{l=1}{\overset{i}{{\displaystyle \prod }}}\left[1-t_l+\left(n-j\right)h\right]},\forall 1<i<n-2,i<j\le n.\end{array}$ (2.8)

③ 利用矩阵A的初始子式表达式，得到：

$\begin{array}{c}{d}_{ii}=\frac{\det A\left[1,\cdots ,i|1,\cdots ,i\right]}{\det A\left[1,\cdots ,i-1|1,\cdots ,i-1\right]}\\ =\left(\begin{array}{c}n-1\\ i-1\end{array}\right)\frac{\underset{k=0}{\overset{n-i-1}{{\displaystyle \prod }}}\left(1-t_i+kh\right)}{\underset{k=0}{\overset{n-i-1}{{\displaystyle \prod }}}\left(1+kh\right)}\underset{l=1}{\overset{i-1}{{\displaystyle \prod }}}\frac{\left(t_i-t_l\right)}{\left[1-t_l+\left(n-i\right)h\right]},1\le i\le n-2.\end{array}$ (2.9)

下面讨论 $d_{n-1,n-1}$， $d_{n,n}$， ${\beta }_{n,n-1}$ 和 $\delta$ 的表达式。

元素 $d_{n-1,n-1}$ 如下：

$d_{n-1,n-1}=-\frac{\det A\left[2,\cdots ,n|1,\cdots ,n-1\right]}{\det A\left[2,\cdots ,n-1|1,\cdots ,n-2\right]}=\left(\begin{array}{c}n-1\\ n-2\end{array}\right)\left(1-t_n\right)\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\frac{\left(t_n-t_l\right)}{\left(1-t_l+h\right)}.$ (2.10)

则元素 $d_{n,n}$ 如下：

$\begin{array}{l}\det A=\det \tilde{B}-z\det \tilde{B}\left[1,\cdots ,n-1\right]\\ =\left[\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)-z\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_l\right)\right]\left(\begin{array}{c}n-1\\ 0\end{array}\right)\cdots \left(\begin{array}{c}n-1\\ n-2\end{array}\right)\frac{{\displaystyle \underset{1\le s<l\le n-1}{\prod }\left(t_l-t_s\right)}}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{1}{{\displaystyle \prod }}}\left(1+kh\right)}\end{array}$ (2.11)

由(2.9)和(2.10)得：

${\displaystyle \underset{i=1}{\overset{n-1}{\prod }}{d}_{ii}}=\left(\begin{array}{c}n-1\\ 0\end{array}\right)\cdots \left(\begin{array}{c}n-1\\ n-2\end{array}\right)\frac{\left(1-t_1+h\right)\left(1-t_n\right)}{\left(1-t_{n-1}+h\right)}\cdot \frac{\underset{l=1}{\overset{n-2}{{\displaystyle \prod }}}\left(1-t_l\right)\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)\underset{1\le s<l\le n-2}{\overset{}{{\displaystyle \prod }}}\left(t_l-t_s\right)}{\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{1}{{\displaystyle \prod }}}\left(1+kh\right)}$ (2.12)

由(2.11)和(2.12)得：

$\begin{array}{c}{d}_{n,n}=-\det A/{\displaystyle \underset{i=2}{\overset{n-1}{\prod }}{d}_{ii}}\\ =\left[z\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_l\right)-\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)\right]\frac{\left(1-t_{n-1}+h\right)}{\left(1-t_1+h\right)\left(1-t_n\right)\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)}\underset{l=1}{\overset{n-2}{{\displaystyle \prod }}}\frac{\left(t_{n-1}-t_l\right)}{\left(1-t_l\right)}.\end{array}$ (2.13)

接下来求参数 ${\beta }_{n,n-1}$，

$\begin{array}{c}{\beta }_{n,n-1}=\frac{\det A\left[1,\cdots ,n-1\right]}{\det A\left[1,\cdots ,n-2\right]}\cdot \frac{\det A\left[2,\cdots ,n-1|1,\cdots ,n-2\right]}{\det A\left[2,\cdots ,n|1,\cdots ,n-1\right]}\\ =\frac{\left(1-t_{n-1}\right)\left(1-t_{n-1}+h\right)\underset{l=1}{\overset{n-2}{{\displaystyle \prod }}}\left(t_{n-1}-t_l\right)}{\left(1-t_n\right)\left(1-t_1+h\right)\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)}.\end{array}$ (2.14)

最后，利用推论2.3得到参数 $\delta$

$\begin{array}{c}\delta =\frac{\det A\left[2,\cdots ,n\right]}{d_{n-1,n-1}\underset{t=3}{\overset{n}{{\displaystyle \prod }}}{d}_{t-2,t-2}{\alpha }_{t-2,t-1}{\beta }_{t-1,t-2}}\\ =\frac{\det B\left[2,\cdots ,n\right]-z\det B\left[2,\cdots ,n-1\right]}{d_{n-1,n-1}\underset{t=3}{\overset{n}{{\displaystyle \prod }}}{d}_{t-2,t-2}{\alpha }_{t-2,t-1}{\beta }_{t-1,t-2}}\\ =\left[t_n\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)-z\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_l\right)\right]\left(\begin{array}{c}n-1\\ 1\end{array}\right)\cdots \left(\begin{array}{c}n-1\\ n-2\end{array}\right)\\ \cdot \frac{\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}{t}_l\underset{2\le s<l\le n-1}{\overset{}{{\displaystyle \prod }}}\left(t_l-t_s\right)}{d_{n-1,n-1}\underset{t=3}{\overset{n}{{\displaystyle \prod }}}{d}_{t-2,t-2}{\alpha }_{t-2,t-1}{\beta }_{t-1,t-2}\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{1}{{\displaystyle \prod }}}\left(1+kh\right)}.\end{array}$ (2.15)

特别的，若 $z=\left(t_n-r{t}_1\right)\frac{\underset{l=2}{\overset{n-1}{{\displaystyle \prod }}}\left(t_n-t_l\right)}{\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}\left(1-t_l\right)},\text{0}\le r<1$。则：

$\{\begin{array}{l}{d}_{n,n}=\frac{\left(1-r\right)t_1\left(1-t_{n-1}+h\right)}{\left(1-t_1+h\right)\left(1-t_n\right)}\underset{l=1}{\overset{n-2}{{\displaystyle \prod }}}\frac{\left(t_{n-1}-t_l\right)}{\left(1-t_l\right)},\\ \delta =\left(\begin{array}{c}n-1\\ 1\end{array}\right)\cdots \left(\begin{array}{c}n-1\\ n-2\end{array}\right)\frac{t_1\left(r-t_n\right)}{\left(1-t_1\right)}\cdot \frac{\underset{l=1}{\overset{n-1}{{\displaystyle \prod }}}{t}_l\left(t_n-t_l\right)\underset{2\le s<l\le n-1}{\overset{}{{\displaystyle \prod }}}\left(t_l-t_s\right)}{d_{n-1,n-1}\underset{t=3}{\overset{n}{{\displaystyle \prod }}}{d}_{t-2,t-2}{\alpha }_{t-2,t-1}{\beta }_{t-1,t-2}\underset{k=0}{\overset{n-2}{{\displaystyle \prod }}}\left(1+kh\right)\cdots \underset{k=0}{\overset{1}{{\displaystyle \prod }}}\left(1+kh\right)}.\end{array}$ (2.16)

结论得证。

根据定理2.4，我们得到形如(1.1)的quasi-h-Bernstein-Vandermonde矩阵是符号序列为 $\left(1,\cdots ,1,-1\right)$ 的广义SR矩阵。

3. quasi-h-Bernstein-Vandermonde矩阵的高精度算法

本节，利用上一节的定理2.4求得的所有参数，给出计算quasi-h-Bernstein-Vandermonde矩阵A的所有特征值的高精度算法。

算法3.1

输入： $h\ge 0$ 和节点 ${\left\{t_i\right\}}_{1\le i\le n}$，其中 $\text{0}<t_1<t_2<\cdots <t_n<1$。

输出：矩阵A的所有特征值。

1) 通过定理2.4计算出矩阵A的所有参数。

2) 利用步骤1所求得的参数，结合算法3 [4] 计算矩阵A的所有特征值。

4. 数值实验

接下来，通过给出数值例子来验证我们所提出的计算特征值的算法的高精度性。

1) 在Matlab中分别用上一节所提出的算法和命令eig计算出矩阵A的所有特征值的计算值 ${\hat{\lambda }}_i$ ：

a) 算法3.1。

b) Matlab中的命令eig。

2) 在Mathematica中计算出矩阵A的所有特征值的准确值 ${\lambda }_i$。

3) 将算法3.1计算出的特征值与MATLAB命令eig计算出的特征值进行比较，并且利用 $\left|{\hat{\lambda }}_i-{\lambda }_i\right|/\left|{\lambda }_i\right|$ 来衡量相对误差。

例子4.1 令 $A=\left(a_{i,j}\right)\in {ℝ}^{15\times 15}$ 是一个quasi-h-Bernstein-Vandermonde矩阵，元素

$a_{i,j}=\{\begin{array}{l}\frac{\left(\begin{array}{c}\text{14}\\ j-1\end{array}\right)\underset{k=0}{\overset{j-2}{{\displaystyle \prod }}}\left(t_i+kh\right)\underset{k=0}{\overset{\text{14}-j}{{\displaystyle \prod }}}\left(1-t_i+kh\right)}{\underset{k=0}{\overset{13}{{\displaystyle \prod }}}\left(1+kh\right)},\left(i,j\right)\ne \left(\text{15},\text{15}\right);\\ \frac{\underset{k=0}{\overset{13}{{\displaystyle \prod }}}\left(t_{\text{15}}+kh\right)}{\underset{k=0}{\overset{13}{{\displaystyle \prod }}}\left(1+kh\right)}-\left(t_{\text{15}}-r{t}_1\right)\frac{\underset{l=2}{\overset{14}{{\displaystyle \prod }}}\left(t_{\text{15}}-t_l\right)}{\underset{l=1}{\overset{14}{{\displaystyle \prod }}}\left(1-t_l\right)},\left(i,j\right)=\left(\text{15},\text{15}\right),\end{array}$

其中 $t_i=1/\left(\text{18}-i\right)$， $i=\text{1},\text{2,}\cdots ,\text{15}$， $h=1/5$ 和 $r=2/3$。谱条件数为：

${\kappa }_2\left(A\right)=\text{7}\text{.648744013234936e}+\text{18}$。

具体实验结果见下面表1与图1。

Table 1. The relative error of the eigenvalues of the matrix A

表1. 矩阵A的特征值的相对误差

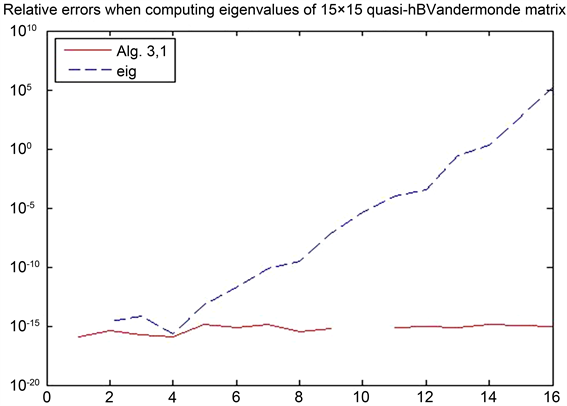
Figure 1. The relative error of the calculated characteristic value

图1. 计算的特征值的相对误差

实验结果表明，Matlab中的命令eig只能确保部分大的特征值是高精度的，但如果特征值非常小时就不能确保其高精度，而文中的算法3.1能够高精度计算所有的特征值。因此，数值实验4.1验证了算法3.1的高精度性。