半经典次临界增长SchrO¨dinger-Poisson方程组变号解的存在性和集中现象
Existence and Concentration of Infinitely Many Sign-Changing Solutions of Semiclassical Subcritical GrowthSchrO¨dinger-Poisson Systems
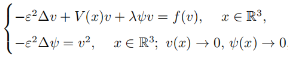
摘要: 在本文中，研究半经典次临界增长 Schrödinger-Poisson 方程组, 当 |x| → ∞ 时, 其中 ε > 0 是小参数，λ, µ > 0 是参数，V : ℝ3 → ℝ 是有界位势函数且局部极小点集 M 非空， 利用下降流不变集方法和截断技巧证明无穷多变号解的存在性，当 ε → 0 时，通过构造惩罚项证明这些解集中在位势函数 V 的局部极小附近。
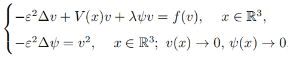
Abstract: In this paper, we study the following semiclassical Schrödinger-Poisson system , where ε > 0 is a small parameter, λ > 0 is a parameter and V : ℝ3 → ℝ is a bounded potential function, the nonlinearity f is superlinear at the origin and at infinity, and is subcritical growth. We proved the existence of infinitely many sign-changing solutions by the method of invariant sets with descending flow and the truncation technique, and proved that these solutions are located near the local minimum point of the potential function V as ε → 0 by the penalization method.
文章引用：王星. 半经典次临界增长SchrO¨dinger-Poisson方程组变号解的存在性和集中现象[J]. 应用数学进展, 2021, 10(4): 1359-1379. https://doi.org/10.12677/AAM.2021.104146

参考文献

[1] Chen, Z., Qin, D. and Zhang, W. (2020) Localized Nodal Solutions of Higher Topological Type For Nonlinear Schrödinger—Poisson System. Nonlinear Analysis, 198, Article ID: 111896.
https://doi.org/10.1016/j.na.2020.111896
[2] Chen, S., Liu, J. and Wang, Z.-Q. (2019) Localized Nodal Solutions for a Critical Nonlinear Schrödinger Equations. Journal of Functional Analysis, 277, 594–640.
https://doi.org/10.1016/j.jfa.2018.10.027
[3] Chen, S. and Wang, Z.-Q. (2017) Localized Nodal Solutions of Higher Topological Type for Semiclassical Nonlinear Schrödinger Equations. Calculus of Variations and Partial Differential
[4] Equations, 56, 1-26.
https://doi.org/10.1007/s00526-016-1094-4
[5] Liu, X., Liu, J. and Wang, Z.-Q. (2019) Localized Nodal Solutions for Quasilinear Schrödinger Equations. Journal of Differential Equations, 267, 7411-7461.
https://doi.org/10.1016/j.jde.2019.08.003
[6] Byeon, J. and Wang, Z.-Q. (2003) Standing Waves with a Critical Frequency for Nonlinear Schrödinger Equations, II. Calculus of Variations and Partial Differential Equations, 18, 207- 219.
https://doi.org/10.1007/s00526-002-0191-8
[7] Ruiz, D. (2006) The Schrödinger–Poisson Equation under the Effect of a Nonlinear Local Term.
[8] Journal of Functional Analysis, 237, 655-674.
https://doi.org/10.1016/j.jfa.2006.04.005
[9] Cerami, G. and Vaira, G. (2010) Positive Solutions for Some Non-Autonomous Schrödinger– Poisson Systems. Journal of Differential Equations, 48, 521-543.
https://doi.org/10.1016/j.jde.2009.06.017
[10] Liu, Z. and Sun, J. (2001) Invariant Sets of Descending Flow in Critical Point Theory with Applications to Nonlinear Differential Equations. Journal of Differential Equations, 172, 257- 299.
https://doi.org/10.1006/jdeq.2000.3867
[11] Liu, J., Liu, X. and Wang, Z.-Q. (2016) Sign-Changing Solutions for Coupled Nonlinear Schrödinger Equations with Critical Growth. Journal of Differential Equations, 261, 7194- 7236.
https://doi.org/10.1016/j.jde.2016.09.018
[12] Tintarev, K. and Fieseler, K.-H. (2007) Concentration Compactness. Functional-Analytic Grounds and Applications. Imperial College Press, London.
https://doi.org/10.1142/p456
[13] Cerami, G., Devillanova, G. and Solimini, S. (2005) Infinitely Many Bound States for Some Nonlinear Scalar Field Equations. Calculus of Variations and Partial Differential Equations, 23, 139-168.
https://doi.org/10.1007/s00526-004-0293-6
[14] Devillanova, G. and Solimini, S. (2002) Concentrations Estimates and Multiple Solutions to Elliptic Problems at Critical Growth. Advances in Difference Equations, 7, 1257-1280.

为你推荐