沿双曲柱面的多元Lagrange插值问题研究

Multivariate Lagrange Interpolation Defined on Hyperbolic Cylinder

摘要: 本文以三元函数Lagrange插值研究结果为基础，对定义于双曲柱面上的Lagrange插值正则性问题进行了较为详尽的研究，基本搞清了这类正则结点组的基本理论和拓扑结构，得到了构造P_n⁽³⁾插值正则结点组的添加双曲柱面法以及构造沿双曲柱面的插值正则结点组的迭加构造法，最后通过实验算例验证了算法的有效性。

Abstract: In this paper, based on the results of Lagrange interpolation for binary functions, the regularization problem of Lagrange interpolation on hyperbolic cylinders is further studied. The basic theory and topological structure of this kind of regular node group are clarified, and the method of adding hyperbolic cylinder to construct the regular node group of ternary Euclidean space interpolation and the superposition method to construct the regular node group of interpolation along hyperbolic cylinder are obtained. Finally, an experimental example is given to verify the effectiveness of the results.

1. 引言

近年来，双曲柱面在日常生活及工业生产中均有着广泛的应用。例如在光学领域中，双曲柱面通常用作透射光栅，在光栅常数不变的情况下，衍射光强会随着双曲线半实轴的变化而变化，当双曲线的半实轴取值较小时，光强分布基本呈单缝衍射的光强分布，随着双曲线半实轴取值的不断增大，衍射光强会逐渐呈“平顶”状分布。但当半实轴取值增大到一定程度时，近似“平顶”状的分布会逐渐减小直至衍射现象消失，从而失去光栅的衍射作用 [1]。因此对沿双曲柱面的多元Lagrange插值问题进行研究是十分必要的。而在插值问题中，结点组的正则性问题是我们首先需要解决的问题。本文结合多元函数插值与逼近的相关理论知识及以往学者对三元函数插值问题的研究 [2] [3]，进一步研究了沿双曲柱面的插值正则性问题，并在文章最后给出实验算例对所得研究结果进行了验证。

2. 基本定义和主要定理

本文主要研究定义于三维欧式空间R³中的双曲柱面 $F=\left\{\left(x,y,z\right)\in R^3|\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\right\}$ 上的Lagrange插

值问题，首先给出一些基本概念。

设 $n\in N$， $d_n=\left(\begin{array}{c}n+3\\ 3\end{array}\right)$， $P_n^{\left(3\right)}$ 是R³中所有全次数小于等于n的三元实系数多项式所构成的空间，即 $P_n^{\left(3\right)}=\left\{{\displaystyle \underset{0\le i+j+k\le n}{\sum }{a}_{ijk}{x}^i{y}^j{z}^k|a_{ijk}\in R}\right\}$。

定义1 [4] 设 $A={\left\{Q_i\right\}}_{i=1}^{d_n}\in R^3$ 且A中的点互不相同，任意给定一组实数组 ${\left\{f_i\right\}}_{i=1}^{d_n}$，在 $P_n^{\left(3\right)}$ 中均能找到唯一一个多项式 $p\left(x,y,z\right)$，使之满足 $p\left(Q_i\right)=f_i,i=1,2,\cdots ,d_n$。则称该插值问题是关于空间 $P_n^{\left(3\right)}$ 的正则插值问题，并称 $A={\left\{Q_i\right\}}_{i=1}^{d_n}$ 为 $P_n^{\left(3\right)}$ 的一个插值正则结点组。

定义2 设F是上文中所定义的一个双曲柱面， $n\in N$，定义 $d_n\left(2\right)$ 为：

$d_n\left(2\right)=\left(\begin{array}{c}n+3\\ 3\end{array}\right)-\left(\begin{array}{c}n+3-2\\ 3\end{array}\right).$ (1)

设 $A={\left\{Q_i\right\}}_{i=1}^{d_n\left(2\right)}\in F$ 且A中的点互不相同，任意给定一组实数组 ${\left\{f_i\right\}}_{i=1}^{d_n\left(2\right)}$，在 $P_n^{\left(3\right)}$ 中均能找到唯一一个

多项式 $p\left(x,y,z\right)$，使之满足 $p\left(Q_i\right)=f_i,i=1,2,\cdots ,d_n\left(2\right)$。则称 $A={\left\{Q_i\right\}}_{i=1}^{d_n\left(2\right)}$ 为沿双曲柱面F的一个n次插

值正则结点组，记为 $A\in I_n^{\left(3\right)}\left(F\right)$。(其中 $A\in I_n^{\left(3\right)}\left(F\right)$ 代表所有位于双曲柱面F上的n次插值正则结点组所构成的集合)。

定义3 设F是上文中所定义的一个双曲柱面， $m\in N$，代数曲线 $C=s\left(F,g\right)$ 是双曲柱面F与m次代数曲面 $g\left(X\right)=0$ 在空间中充分相交所得到的曲线，定义 $e_n\left(2,m\right)$ 为：

$e_n\left(2,m\right)=\left(\begin{array}{c}n+3\\ 3\end{array}\right)-\left(\begin{array}{c}n+3-2\\ 3\end{array}\right)-\left(\begin{array}{c}n+3-m\\ 3\end{array}\right)+\left(\begin{array}{c}n+3-m-2\\ 3\end{array}\right).$ (2)

设 $A={\left\{Q_i\right\}}_{i=1}^{e_n\left(2,m\right)}\in C$ 且A中的点互不相同，任意给定一组实数组 ${\left\{f_i\right\}}_{i=1}^{e_n\left(2,m\right)}$，在 $P_n^{\left(3\right)}$ 中均能找到唯一一个多项式 $p\left(x,y,z\right)$，使之满足 $p\left(Q_i\right)=f_i,i=1,2,\cdots ,e_n\left(2,m\right)$。则称 $A={\left\{Q_i\right\}}_{i=1}^{e_n\left(2,m\right)}$ 为沿代数曲线 $C=s\left(F,g\right)$

的一个n次插值正则结点组，记为 $A\in I_n^{\left(3\right)}\left(C\right)$。(其中 $I_n^{\left(3\right)}\left(C\right)$ 代表所有位于代数曲线 $C=s\left(F,g\right)$ 上的n次插值正则结点组所构成的集合)。

定理1 [5] $A={\left\{Q_i\right\}}_{i=1}^{d_n}$ 是 $P_n^{\left(3\right)}$ 的插值正则结点组的充要条件是点组 $A={\left\{Q_i\right\}}_{i=1}^{d_n}$ 不同时落在代数曲面 $\Gamma$ 上(其中 $\Gamma$ 为 $P_n^{\left(3\right)}$ 中的任意代数曲面)。

本文主要结果如下：

定理2 设F是上文中所定义的一个双曲柱面， $n\in N$， $A={\left\{Q_i\right\}}_{i=1}^{d_n}$ 是 $P_n^{\left(3\right)}$ 的一个插值正则结点组， $B={\left\{Q_i\right\}}_{i=1}^{d_{n+2}\left(2\right)}$ 是沿双曲柱面F的一个 $n+2$ 次插值正则结点组(即 $B\in I_{n+2}^{\left(3\right)}\left(F\right)$ )，且 $A\cap B=\varnothing$，则 $C=A\cup B$ 必定构成空间 $P_{n+2}^{\left(3\right)}$ 的插值正则结点组。

定理3 设 $m\in N,n\in N$，F是上文中所定义的一个双曲柱面，代数曲线 $C=s\left(F,g\right)$ 是双曲柱面F与m次代数曲面 $g\left(X\right)=0$ 在空间中充分相交所得到的曲线，在F上但不经过曲线 $C=s\left(F,g\right)$ 选取沿该曲面的一个n次插值正则结点组 $A\in I_n^{\left(3\right)}\left(F\right)$，同时在曲线 $C=s\left(F,g\right)$ 上选取其一个 $n+m$ 次插值正则结点组 $B\in I_{n+m}^{\left(3\right)}\left(C\right)$，则 $A\cup B\in I_{n+m}^{\left(3\right)}\left(F\right)$。

3. 定理的证明

为了证明本文的主要结果，首先给出如下引理。

引理 [6] 设 $d_n\left(2\right)$ 为 中所定义的公式，则 $A={\left\{Q_i\right\}}_{i=1}^{d_n\left(2\right)}$ 能够做成沿双曲柱面F的n次插值正则结点组的充要条件是对于任何满足零插值条件

$p\left(Q_i\right)=0,\forall Q_i\in A$

的多项式 $p\left(x,y,z\right)\in P_n^{\left(3\right)}$，均存在如下分解：

$p\left(x,y,z\right)=F\left(x,y,z\right)r\left(x,y,z\right).$

其中当 $n\ge 2$ 时， $r\left(x,y,z\right)\in P_{n-2}^{\left(3\right)}$，当 $n<2$ 时， $r\left(x,y,z\right)\equiv 0$。

证明：只需证明必要性。因为 $A={\left\{Q_i\right\}}_{i=1}^{d_n\left(2\right)}\in I_n^{\left(3\right)}\left(F\right)$，不妨设 $I_1=\langle F\rangle$， $I_2=\langle p\rangle$。

又因为 $p\left(Q_i\right)=0,\forall Q_i\in A$。由定义2知，沿曲面 $F\left(x,y,z\right)=0$ 恒有 $p\left(x,y,z\right)=0$。则 $V\left(I_1\right)\subset V\left(I_2\right)$， $I\left(V\left(I_1\right)\right)\supset I\left(V\left(I_2\right)\right)$。

又由 $I\left(V\left(I_1\right)\right)=\sqrt{I_1}=I_1$， $I\left(V\left(I_2\right)\right)=\sqrt{I_2}\supset I_2$，有 $I_1\supset I_2$。

所以存在多项式 $r\left(x,y,z\right)\in P_{n-2}^{\left(3\right)}$，使得 $p\left(x,y,z\right)=F\left(x,y,z\right)r\left(x,y,z\right)$。

定理2的证明：点组C中所包含的点数为

$\left(\begin{array}{c}n+3\\ 3\end{array}\right)+\left[\left(\begin{array}{c}n+5\\ 3\end{array}\right)-\left(\begin{array}{c}n+5-2\\ 3\end{array}\right)\right]=\left(\begin{array}{c}n+5\\ 3\end{array}\right),$

这恰好等于空间 $P_{n+2}^{\left(3\right)}$ 的维数。

下面采用反证法对其进行证明。

假设 $C=A\cup B$ 不是空间 $P_{n+2}^{\left(3\right)}$ 的正则结点组，则根据定理1知，必存在不恒为零的多项式 $p\left(x,y,z\right)$ $\in P_{n+2}^{\left(3\right)}$，使得 $p\left(Q_i\right)=0,\forall Q_i\in C$。特别地有 $p\left(Q_i\right)=0,\forall Q_i\in B$。

因为 $B\in I_{n+2}^{\left(3\right)}\left(F\right)$，则由引理知，存在 $r\left(x,y,z\right)\in P_n^{\left(3\right)}$，使得

$p\left(x,y,z\right)=F\left(x,y,z\right)r\left(x,y,z\right).$

又因为 $p\left(Q_i\right)=0,\forall Q_i\in A$。所以 $0=p\left(Q_i\right)=F\left(Q_i\right)r\left(Q_i\right),\forall Q_i\in A$。

但 $F\left(Q_i\right)\ne 0,\forall Q_i\in A$。所以 $r\left(Q_i\right)=0,\forall Q_i\in A$。而 $A={\left\{Q_i\right\}}_{i=1}^{d_n}$ 是 $P_n^{\left(3\right)}$ 的插值正则结点组，且 $r\left(x,y,z\right)$ $\in P_n^{\left(3\right)}$。

所以 $r\left(x,y,z\right)\equiv 0$。进而 $p\left(x,y,z\right)\equiv 0$。这与假设矛盾，故C是 $P_{n+2}^{\left(3\right)}$ 的插值正则结点组。

定理3的证明：点组 $A\cup B$ 所含的点数为

$\begin{array}{l}\left[\left(\begin{array}{c}n+3\\ 3\end{array}\right)-\left(\begin{array}{c}n+1\\ 3\end{array}\right)\right]+[\left(\begin{array}{c}n+m+3\\ 3\end{array}\right)-\left(\begin{array}{c}n+m+1\\ 3\end{array}\right)-\left(\begin{array}{c}n+m+3-m\\ 3\end{array}\right)+\left(\begin{array}{c}n+m+1-m\\ 3\end{array}\right)]\\ =\left(\begin{array}{c}n+m+3\\ 3\end{array}\right)+\left(\begin{array}{c}n+m+1\\ 3\end{array}\right)\end{array}$

这恰好等于沿双曲柱面F的 $n+m$ 次插值正则结点组中所含的点数。

假设存在多项式 $p\left(x,y,z\right)\in P_{n+m}^{\left(3\right)}$，使得对 $\forall Q_i\in A\cup B$ 有 $p\left(Q_i\right)=0$。根据引理，只需证明存在多项式 $r\left(x,y,z\right)\in P_{n+m-2}^{\left(3\right)}$，使得 $p\left(x,y,z\right)=F\left(x,y,z\right)r\left(x,y,z\right)$ 成立。

因为 $p\left(x,y,z\right)\in P_{n+m}^{\left(3\right)}$ 且 $p\left(Q_i\right)=0,\forall Q_i\in B$。而 $B\in I_{n+m}^{\left(3\right)}\left(C\right)$。

所以，存在多项式 $\alpha \left(x,y,z\right)\in P_{n+m-2}^{\left(3\right)},\beta \left(x,y,z\right)\in P_n^{\left(3\right)}$，使得

$p\left(x,y,z\right)=\alpha \left(x,y,z\right)F\left(x,y,z\right)+\beta \left(x,y,z\right)g\left(x,y,z\right).$ (3)

又因为

$p\left(Q_i\right)=0,\forall Q_i\in A.$ (4)

将(4)代入(3)中有 $\beta \left(Q_i\right)g\left(Q_i\right)=0,\forall Q_i\in A$。但 $g\left(Q_i\right)\ne 0,\forall Q_i\in A$。故 $\beta \left(Q_i\right)=0,\forall Q_i\in A$。

又由于 $A\in I_n^{\left(3\right)}\left(F\right),\beta \left(x,y,z\right)\in P_n^{\left(3\right)}$，则依据引理知， $\exists \tilde{r}\left(x,y,z\right)\in P_{n-2}^{\left(3\right)}$，使得

$\beta \left(x,y,z\right)=F\left(x,y,z\right)\tilde{r}\left(x,y,z\right).$ (5)

将(5)代入(3)式得 $p\left(x,y,z\right)=F\left(x,y,z\right)r\left(x,y,z\right)$。证毕。

4. 实验算例

设被插值函数为： $f\left(x,y,z\right)=\sqrt{x^2+y^2+z^2}$，双曲柱面方程为： $x^2-y^2=1$。取点 $Q_1\left(0,1,1\right)\in R_3$，则

$Q_1\left(0,1,1\right)\in P_0^{\left(3\right)}$，在此双曲柱面上任取互异的9个点(如图1所示)： $Q_2\left(1,0,2\right)$， $Q_3\left(1,0,-2\right)$， $Q_4\left(2,\sqrt{3},3\right)$，

$Q_5\left(2,-\sqrt{3},3\right)$， $Q_6\left(-2,\sqrt{3},3\right)$， $Q_7\left(-2,-\sqrt{3},3\right)$， $Q_8\left(3,\sqrt{8},4\right)$， $Q_9\left(3,-\sqrt{8},4\right)$， $Q_{10}\left(-3,\sqrt{8},4\right)$。

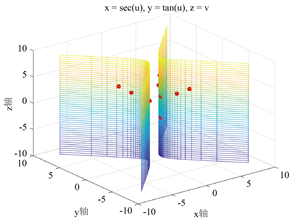
Figure 1. Renderings of hyperbolic cylinder

图1. 双曲柱面取点效果图

则根据定理2可得，点组 $\left\{Q_1,Q_2,\cdots ,Q_{10}\right\}$ 构成空间 $P_2^{\left(3\right)}$ 的插值正则结点组，且所确定的唯一一条插值函数为：

$p\left(x,y,z\right)=-1.3869x^2+0.4807y^2+0.8965z^2+\mathrm{0.0370.}$

经计算求得被插值函数和插值函数在点 $\left(0,0,1\right)$ 处的函数值分别为： $f\left(0,0,1\right)=1.0000$， $p\left(0,0,1\right)=$ $0.9335$。误差为 $r=\left|1.0000-0.9335\right|=0.0665$。