椭球运动的状态约束问题

State Constrain Problem of Ellipsoidal Motions

摘要: 本文研究了椭球运动的状态约束问题，其中椭球可以在状态约束作用下向给定目标集运动。利用Hamilton-Jacobi-Bellman (HJB)方程，给出了状态约束问题的闭环解。最后，给出求解方法以及数值算例。仿真结果表明，状态约束能够保证椭球在合理的状态范围内，最终运动到达目标集。

Abstract: The paper deals with the problem of state constrain of ellipsoidal motion, where the virtual ellipsoid can move to the target set under state constrain. We present solutions of this problem in the class of closed-loop (feedback) controls based on Hamilton-Jacobi-Bellman (HJB) equation. Finally, we give a solution method and numerical examples. Simulation results verify that the state constraint can ensure that the ellipsoidal motions within a reasonable range of states and finally reaches the target set.

1. 引言

编队控制是当前多智能体系统研究的热点问题之一。其所考察的智能体对象包括无人机 [1]、舰艇 [2]、卫星 [3]、机器人 [4] 等，其应用涉及军事、航天、工业等诸多领域。该类控制问题是研究多智能体系统根据分布式任务要求，在向特定目标或方向的运动过程中，保持预定的几何形态，同时又能满足环境约束的控制问题。编队控制的研究内容主要包括如下五个方面：队形生成、队形保持、队形切换、编队避障和编队自适应问题。

近年来，针对不同的应用环境和约束条件，学者们提出了多种用于多智能体系统的控制算法。常见编队控制方法主要有长僚机法 [5] [6] [7] [8]、基于行为的方法 [9] [10]、虚拟结构法 [11] [12] 和人工势场法 [13] [14]。长僚机法在多智能体领域也叫跟随领航者法(Leader-follower方法)，即指定队形中的某架无人机作为Leader，其他的无人机作为Follower跟随Leader运动。这种方法将队形控制问题转化为Follower跟踪Leader的朝向和位置的问题。基于行为的编队控制方法是指，基于行为的控制器由一系列简单的基本动作组成，每个无人机都有自己的目标或任务，根据每个无人机的输入、输出构成交互的行为网络。虚拟结构法是将多智能体系统的编队看作虚拟的刚性结构，每个智能体跟踪刚性结构上一个位置固定的虚拟点运动。人工势场法的基本思想是借鉴物理学方面的概念，飞行环境中的障碍物对无人机产生排斥力，目标点对无人机产生吸引力，最后通过求合力来控制移动多智能体的运动。

Kurzhansk提出了一种基于虚拟椭球运动的多智能体系统的编队控制方法的理论框架 [15]。文中假设了一个运动的虚拟椭球容器为 $E_c\left[t\right]$，并将每个智能体视为体积较小的球体。设多智能体系统从特定的初始位置出发，集结于虚拟的椭球 $E_c\left[t\right]$ 内部以形成集群，并跟随椭球运动到达指定的目标集。在向目标集运动的过程中，需确保在 $E_c\left[t\right]$ 内部的球体无碰撞发生，且 $E_c\left[t\right]$ 需要设法规避已知的障碍物。需要指出的是，虚拟椭球的运动可由其中心的坐标和配置矩阵所满足的线性微分方程所完全刻画。同时，智能体的运动需与椭球的运动以及其它智能体的运动保持一致。Kurzhanski指出，可以通过定义合适的值函数，利用动态规划的方法来获得虚拟椭球以及多智能体系统的运动轨迹，从而给出了多智能体系统的合成控制的一个求解理论框架。Kurzhanski的相关工作可参见文献 [16] [17]。

事实上，我们可将Kurzhanski提出的基于虚拟椭球的多智能体系统的编队控制方法视为编队控制中的虚拟结构法的一种改进。传统的虚拟结构法使得编队必须刚性运动，从而限制了该方法的应用范围。而基于虚拟椭球的编队控制方法，不仅继承了传统虚拟结构法容易整体描述系统行为、可取得较高编队控制精度等优点，还完全弥补了传统虚拟结构方法中刚性运动的缺陷。

2012年，Kurzhansk研究了虚拟椭球的目标控制问题，其中椭球可以在最优控制作用下向给定目标集运动，既能保证目标误差尽可能小，又能避免使用取值“过大”的控制 [18]。若没有状态约束，目标误差可能太大，这时可能需要“过大”的控制，因此使用状态约束是必然的。2013年，Kurzhansk研究了状态约束下的虚拟椭球的目标控制问题，但只考虑了椭球的形状，并未考虑椭球的中心 [19]。本文在Kurzhanski的工作基础上进一步研究并实现了对虚拟椭球的具有状态约束功能的最优目标控制。首先，我们需要同时获得对椭球中心和配置矩阵的两个最优控制。其次，针对编队的实际情形，我们对其目标函数进行优化，在考虑运动过程中需满足的状态约束的同时，还将对椭球的中心以及配置矩阵的控制约束统一纳入到值函数的定义中去，从而实现对椭球的最优控制。最后，我们对此进行了数值仿真，验证了该方法的有效性。

2. 问题描述

定义1定义 ${ℝ}^n$ 上的非退化椭球 [20]

$\epsilon \left(q,Q\right)=\left\{p\in {ℝ}^n:\langle p-q,Q^{-1}\left(p-q\right)\le 1\rangle \right\},$

其中 $q\in {ℝ}^n$ 为椭球 $\epsilon \left(q,Q\right)$ 的中心， $Q\in {ℝ}^{n\times n}$ 为其配置矩阵且对称正定。 $\langle y,z\rangle$ 表示两个向量的内积， $Q^{-1}$ 表示Q的逆矩阵， $x^{\prime }$ 表示x的转置向量。考察如下形式的虚拟椭球运动

$E_c\left[t\right]=\epsilon \left(q\left(t\right),Q\left(t\right)\right),$

其中 $t\in \left[t_0,\theta \right]$， $q\left(t\right)\in {ℝ}^n$ 和 $Q\left(t\right)\in {ℝ}^{n\times n}$ 分别是 $E_c\left[t\right]$ 在t时刻的中心和配置矩阵。通常 $E_c\left[t\right]\left(t\in \left[t_0,\theta \right]\right)$ 也被称为椭球值轨迹管(ellipsoid-valued trajectories tubes)。

在区间 $\left[t_0,\theta \right]$ 上，椭球 $E_c\left[t\right]$ 的运动方程可以由如下系统定义：

$\stackrel{\dot{}}{q}\left(t\right)=A_q\left(t\right)q\left(t\right)+B_q\left(t\right)u\left(t,q\right),q\left(t_0\right)=q_0,$ (1)

$\stackrel{\dot{}}{Q}\left(t\right)=T\left(t\right)Q\left(t\right)+Q\left(t\right)T^{\prime }\left(t\right)+B_Q\left(t\right)U\left(t,Q\right){B^{\prime }}_Q\left(t\right),Q\left(t_0\right)=Q_0\text{,}$ (2)

其中 $q\left(t\right)$ 和 $Q\left(t\right)$ 是系统(1)和(2)的状态变量。 $u\left(t,q\right)\in {ℝ}^{m_1}$ 和 $U\left(t,Q\right)\in {ℝ}^{m_2\times m_2}$ 是控制变量，且 $U\left(t,Q\right)$ 是对称矩阵。假设系统(1)和(2)的矩阵系数 $A_q\left(t\right)\in {ℝ}^{n\times n}$， $B_q\left(t\right)\in {ℝ}^{n\times m_1}$， $B_Q\left(t\right)\in {ℝ}^{n\times m_2}$ 和 $T\left(t\right)\in {ℝ}^{n\times n}$ 关于t连续可微，且 $T\left(t\right)$ 是对称矩阵。

假设系统(1)和(2)的容许控制集合为 $u\left(t,q\right)\subseteq {ℝ}^{m_1}$ 和 $U\left(t,Q\right)\subseteq {ℝ}^{m_2\times m_2}$，其中 $u\left(t,q\right)$ 和 $U\left(t,Q\right)$ 是给定的凸紧集。对于任意 $u\left(t,q\right)\in u\left(t,q\right)$ 和 $U\left(t,Q\right)\in U\left(t,Q\right)$，有

${\displaystyle \underset{t_0}{\overset{\theta }{\int }}\left(\langle u\left(t,q\right),u\left(t,q\right)\rangle +\left[U\left(t,Q\right),U\left(t,Q\right)\right]\right)\text{d}t\le {\mu }^2,}$ (3)

其中常数 ${\mu }_1,{\mu }_2\ge 0$，而 $\left[U,U\right]=\text{tr}{U}^{\prime }U$ 表示矩阵内积。称(3)式为系统的控制约束。

在系统(1)和(2)运动的过程中，可以通过约束 $Q\left(t\right)$ 来限制 $E_c\left[t\right]$ 的大小，即

$\left[Q\left(t\right),Q\left(t\right)\right]\le {\delta }^2,$ (4)

${\sigma }^2\le \left[Q\left(t\right),Q\left(t\right)\right]\text{,}$ (5)

其中常数 $\sigma ,\delta >0$， $I_{n\times n}\in {ℝ}^{n\times n}$ 表示 $n\times n$ 维的单位矩阵。此时， $E_c\left[t\right]$ 被限制在半径为 $\sqrt{\frac{\sigma }{n}}$ 的最大内接球和半径为 $\sqrt{\frac{\delta }{n}}$ 的最小外接球之间。称(4)和(5)式为系统的状态约束。

注1 在可能的约束条件中，考虑体积约束

$0<\sigma \le vol\epsilon \left(0,Q\left(t\right)\right)\le \delta ,$

也是有意义的，其中vol是椭球的体积。不过本文并不对这种情况进行细节叙述。

假设 $E_c\left[t\right]$ 的目标椭球 $E_M=\epsilon \left(m,M\right)$，其中 $m\in {ℝ}^n$ 是目标椭球的中心， $M\in {ℝ}^{n\times n}$ 是其配置矩阵且对称正定。定义目标椭球 $E_M=\epsilon \left(m,M\right)$ 的邻域为如下目标集：

$E_{\omega }=\left\{\left(q,Q\right)\in {ℝ}^n\times {ℝ}^{n\times n}|\langle q-m,q-m\rangle \le {\omega }_1^2,\left[Q-M,Q-M\right]\le {\omega }_2^2,{\omega }_1,{\omega }_2>0\right\}.$ (6)

问题1对于系统(1)和(2)，给定时间区间 $\left[t_0,\theta \right]$。假设系统的初始状态为 $\left\{t_0,q\left(t_0\right),Q\left(t_0\right)\right\}$，则初始椭球为 $E_c\left[t_0\right]=\epsilon \left(q\left(t_0\right),Q\left(t_0\right)\right)$。在约束条件(3)、(4)和(5)下，寻找最优反馈控制 $u\left(t,q\right)$ 和 $U\left(t,Q\right)$ 使得，在 $t=\theta$ 时， $E_c\left[t\right]$ 能够到达目标椭球的邻域 $E_{\omega }$。

为了寻找问题1的最优反馈控制 $u\left(t,q\right)$ 和 $U\left(t,Q\right)$，定义目标函数

$\begin{array}{c}\Psi \left(u(\cdot ),U(\cdot )\right)={\displaystyle \underset{t_0}{\overset{\theta }{\int }}\left(\langle u\left(t,q\right),u\left(t,q\right)\rangle +\left[U\left(t,Q\right),U\left(t,Q\right)\right]\right)\text{d}t}\\ +{\xi }_1\langle q\left(\theta \right)-m,q\left(\theta \right)-m\rangle +{\xi }_2\left[Q\left(\theta \right)-M,Q\left(\theta \right)-M\right]\\ =\underset{u,U}{\min },\end{array}$ (7)

成立，其中 ${\xi }_1,{\xi }_2>0$。

注2在上述问题3.1中，方程(1)和(2)可以独立处理。

3. 问题求解

为方便解决上述问题1，将矩阵转化成向量。设 $A=\left(a_{ij}\right)\in {ℝ}^{n\times n}$，引入符号

$\bar{A}={\left[a_{11},a_{12},\cdots ,a_{1n},a_{21},a_{22},\cdots ,a_{2n},\cdots ,a_{n1},a_{n2},\cdots ,a_{nn}\right]}^{\prime }.$

设 $B=\left(b_{ij}\right)\in {ℝ}^{n\times n}$，定义A和B的Kronecker积(又称张量积)

$A\otimes B=\left[\begin{array}{ccc}{a}_{11}B& \cdots & a_{1n}B\\ ⋮& \ddots & ⋮\\ a_{n1}B& \cdots & a_{nn}B\end{array}\right]\in {ℝ}^{n^2\times n^2}.$

使用 $\overline{AXB}=\left(A\otimes B^{\prime }\right)\bar{X}$ 将(2)式改写为

$\bar{Q}\left(t\right)=\left(T\left(t\right)\otimes I\right)\bar{Q}\left(t\right)+\left(I\otimes T\left(t\right)\right)\bar{Q}\left(t\right)+\left(B_Q\left(t\right)\otimes B_Q\left(t\right)\right)\bar{U}\left(t,Q\right).$

记 $A\left(t\right)=T\left(t\right)\otimes I+I\otimes T\left(t\right)$， $B\left(t\right)=B_Q\left(t\right)\otimes B_Q\left(t\right)$，则有

$\stackrel{\dot{}}{\bar{Q}}\left(t\right)=A\left(t\right)\bar{Q}\left(t\right)+B\left(t\right)\bar{U}\left(t,Q\right).$

引入值函数

$\begin{array}{l}{V}_E\left(t,q,\bar{Q}\right)=\underset{u,\bar{U}}{\min }{\displaystyle \underset{t}{\overset{\theta }{\int }}\left(\langle u\left(\tau ,q\right),u\left(\tau ,q\right)\rangle +\left[U\left(\tau ,Q\right),U\left(\tau ,Q\right)\right]\right)\text{d}t}\\ +{\xi }_1\langle q\left(\theta \right)-m,q\left(\theta \right)-m\rangle +{\xi }_2\left[Q\left(\theta \right)-M,Q\left(\theta \right)-M\right]\end{array}$ (8)

得到HJB方程 [21]

$\begin{array}{l}\frac{\partial V_E}{\partial t}+\underset{u,\bar{U}}{\min }\{\langle \frac{\partial V_E}{\partial q},A_q\left(t\right)q+B_q\left(t\right)u\left(t,q\right)\rangle +\langle \frac{\partial V_E}{\partial \bar{Q}},A\left(t\right)\bar{Q}+B\left(t\right)\bar{U}\left(t,Q\right)\rangle \\ +\langle u\left(t,q\right),u\left(t,q\right)\rangle +\langle \bar{U}\left(t,Q\right),\bar{U}\left(t,Q\right)\rangle \}=0.\end{array}$ (9)

边界条件为

$V_E\left(\theta ,q\left(\theta \right),\bar{Q}\left(\theta \right)\right)={\xi }_1\langle q\left(\theta \right)-m,q\left(\theta \right)-m\rangle +{\xi }_2\left[Q\left(\theta \right)-M,Q\left(\theta \right)-M\right].$ (10)

则(8)式定义的值函数为(9)式所示的HJB方程的解。记

$\begin{array}{l}H\left(t,u\left(t\right),\bar{U}\left(t\right)\right)=\langle \frac{\partial V_E}{\partial q},A_q\left(t\right)q+B_q\left(t\right)u\left(t,q\right)\rangle +\langle \frac{\partial V_E}{\partial \bar{Q}},A\left(t\right)\bar{Q}+B\left(t\right)\bar{U}\left(t,Q\right)\rangle \\ +\langle u\left(t,q\right),u\left(t,q\right)\rangle +\langle \bar{U}\left(t,Q\right),\bar{U}\left(t,Q\right)\rangle .\end{array}$

则(9)式等价于

$\{\begin{array}{l}\frac{\partial V_E}{\partial t}+H\left(t,u,\bar{U}\right)=0,\\ \frac{\partial H\left(t,u,\bar{U}\right)}{\partial u}=0,\\ \frac{\partial H\left(t,u,\bar{U}\right)}{\partial \bar{U}}=0.\end{array}$

首先对 $H\left(t,u,\bar{U}\right)$ 分别关于u和U求偏导，得到

$u\left(t,q\right)=-\frac{1}{2}{B^{\prime }}_q\left(t\right)\frac{\partial V_E}{\partial q},$ (11)

$U\left(t,\bar{Q}\right)=-\frac{1}{2}{B}^{\prime }\left(t\right)\frac{\partial V_E}{\partial \bar{Q}}.$ (12)

将(11)、(12)式带入 $\frac{\partial V_E}{\partial t}+H\left(t,u\left(t\right),\bar{U}\left(t\right)\right)=0$，得到

$\begin{array}{l}\frac{\partial V_E}{\partial t}+\langle \frac{\partial V_E}{\partial q},A_q\left(t\right)q\rangle -\frac{1}{4}\langle \frac{\partial V_E}{\partial q},B_q\left(t\right){B^{\prime }}_q\left(t\right)\frac{\partial V_E}{\partial q}\rangle +\langle \frac{\partial V_E}{\partial \bar{Q}},A\left(t\right)\bar{Q}\rangle \\ -\frac{1}{4}\langle \frac{\partial V_E}{\partial \bar{Q}},B\left(t\right)B^{\prime }\left(t\right)\frac{\partial V_E}{\partial \bar{Q}}\rangle =0.\end{array}$ (13)

上述表达式是状态变量和值函数的空间导数的二次形式，我们可假设值函数为二次形式

$V_E\left(t,q,Q\right)=\langle q,p\left(t\right)q\rangle +\langle q,k\left(t\right)\rangle +\langle \bar{Q},P\left(t\right)\bar{Q}\rangle +\langle \bar{Q},K\left(t\right)\rangle +s\left(t\right)\text{,}$ (14)

其中 $P\left(t\right)$ 和 $p\left(t\right)$ 对称且正定， $P\left(t\right)=P\left(t\right)\otimes I_{n\times n}$， $K\left(t\right)=\bar{K}\left(t\right)$。函数 $V_E\left(t,q,\bar{Q}\right)$ 分别对t、q和 $\bar{Q}$ 求偏导，有

$\begin{array}{l}\frac{\partial V_E}{\partial t}=\langle \stackrel{\dot{}}{q},\stackrel{\dot{}}{p}\left(t\right)q\rangle +\langle q,\stackrel{\dot{}}{k}\left(t\right)\rangle +\langle \bar{Q},\stackrel{\dot{}}{P}\left(t\right)\bar{Q}\rangle +\langle \bar{Q},\stackrel{\dot{}}{K}\left(t\right)\rangle +\stackrel{\dot{}}{s}\left(t\right)\text{,}\\ \frac{\partial V_E}{\partial q}=2p\left(t\right)q+k\left(t\right),\frac{\partial V_E}{\partial \bar{Q}}=2P\left(t\right)\bar{Q}+K\left(t\right).\end{array}$

于是(11)、(12)式可改写为

$u\left(t,q\right)=-\frac{1}{2}{B^{\prime }}_q\left(t\right)\left(2p\left(t\right)q+k\left(t\right)\right),$ (15)

$\bar{U}\left(t,Q\right)=-\frac{1}{2}{B}^{\prime }\left(t\right)\left(2P\left(t\right)\bar{Q}+K\left(t\right)\right).$ (16)

将(14)式带入(10)和(13)式，得到一组关于(14)式中未知参数 $P\left(t\right)$ 、 $K\left(t\right)$ 、 $p\left(t\right)$ 、 $k\left(t\right)$ 、 $s\left(t\right)$ 的方程组

$\begin{array}{l}\stackrel{\dot{}}{p}\left(t\right)+2p\left(t\right)A_q\left(t\right)-p\left(t\right)B_q\left(t\right){B^{\prime }}_q\left(t\right)p\left(t\right)=0,p\left(\theta \right)={\xi }_1{I}_{n\times n},\\ \stackrel{\dot{}}{k}\left(t\right)+{A^{\prime }}_q\left(t\right)k\left(t\right)-p\left(t\right)B_q\left(t\right){B^{\prime }}_q\left(t\right)k\left(t\right)=0,k\left(\theta \right)=-2{\xi }_{1}m,\\ \stackrel{\dot{}}{P}\left(t\right)+2P\left(t\right)A\left(t\right)-P\left(t\right)B\left(t\right)B^{\prime }\left(t\right)P\left(t\right)=0,P\left(\theta \right)={\xi }_2{I}_{n^2\times n^2},\\ \stackrel{\dot{}}{K}\left(t\right)+A^{\prime }\left(t\right)K\left(t\right)-P\left(t\right)B\left(t\right)B^{\prime }\left(t\right)K\left(t\right)=0,K\left(\theta \right)=-2{\xi }_2\bar{M},\\ \stackrel{\dot{}}{s}\left(t\right)-\langle k\left(t\right),k\left(t\right)\rangle -\langle K\left(t\right),K\left(t\right)\rangle =0,\\ s\left(\theta \right)={\xi }_1\langle m,m\rangle +{\xi }_2\langle \bar{M},\bar{M}\rangle .\end{array}$ (17)

因为系统(1)和(2)的矩阵系数连续可微，所以方程(9)和(10)存在唯一的解，下面的定理成立。

定理1通过求解(14)式所示的值函数，可以得到系统(1)和(2)的解，其中(14)式的未知参数由方程组(17)确定。此时，最小化值函数的最优控制 $u\left(t,q\right)$ 和 $U\left(t,\bar{Q}\right)$ 由(15)和(16)给出。

因为方程组(17)涉及非线性项，所以即使对于这种比较简单的模型，我们也难以获得解析式，本文着重考虑数值解。运用显示欧拉法进行数值离散化，最后通过仿真软件Matlab得到椭球值轨迹管。

4. 数值仿真

为验证状态约束对椭球运动的控制问题的影响，本节考察数值仿真结果。仿真包括2个情景，分别是不考虑状态约束和考虑状态约束下的椭球运动。在所有仿真中，采用公式(7)所示的目标函数求解系统(1)和(2)，系统的各项参数取值为

$\begin{array}{l}{q}_0={\left[0,0\right]}^{\prime },Q_0=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right],t_0=0,\theta =1,\\ A_q=\left[\begin{array}{cc}4t& 0\\ 0& 4t\end{array}\right],B_q=\left[\begin{array}{cc}2t& t\\ t& 2t\end{array}\right],T=\left[\begin{array}{cc}-3t& 0\\ 0& -3t\end{array}\right],B_Q=\left[\begin{array}{cc}\cos \left(\pi t\right)& -\sin \left(\pi t\right)\\ \sin \left(\pi t\right)& \cos \left(\pi t\right)\end{array}\right].\end{array}$

目标椭球中心和配置矩阵分别为

$m={\left[1,1\right]}^{\prime },M=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right].$

(7)中的未知系数分别为

${\xi }_1=2,{\xi }_2=\mathrm{6.8.}$

当存在状态约束时，取系数 ${\delta }^2=2.5,{\sigma }^2=1.5$。图1给出无状态约束下的椭球 $E_c\left[t\right]$ 的轨迹管，图2给出有状态约束下的椭球 $E_c\left[t\right]$ 的轨迹管。从图1和图2的仿真结果可以看出，当不考虑状态约束时，椭球轨迹管变化较大，此时，要想使得目标误差尽可能小，必须取更大的控制，很可能导致“过大”的控制；当考虑状态约束时，椭球轨迹管变化较小，此时椭球在控制作用下到达目标集。

当存在状态约束时，验证 $E_c\left[t\right]$ 的终端椭球 $E_c\left[1\right]$ 是否到达目标集。给出终端椭球和目标椭球比较图，仿真结果如图3和图4所示。如图3， $E_c\left[t\right]$ 的中心到达目标集。如图4， $E_c\left[t\right]$ 的配置矩阵与目标椭球的配置矩阵几乎重合，显然到达目标集。因此说明，椭球可以在状态约束作用下到达目标集。

5. 结论

本文提出一种通过状态约束限制目标函数来实现椭球运动的方法，该方法使得值函数中的未知参数可以用非线性方程来表示，进而可以求解值函数。

针对虚拟椭球的三维情形，运用本文的方法可以得到类似的结果，只不过运算时间较长。

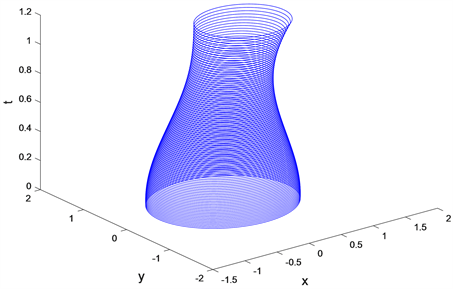
Figure 1. Ellipsoidal tubes of trajectories for the E_c [t] with no regard of the state constraint

图1. 无状态约束下的椭球E_c [t]的轨迹管

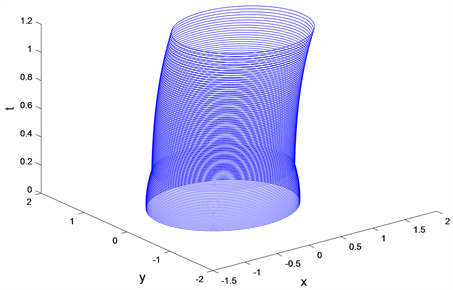
Figure 2. Ellipsoidal tubes of trajectories for the E_c [t] with regard of the state constraint

图2. 有状态约束下的椭球E_c [t]的轨迹管

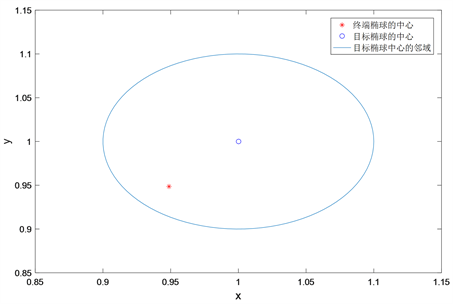
Figure 3. The comparison diagram of the center of the terminal ellipsoid and the target ellipsoid with state constraint

图3. 终端椭球和目标椭球中心比较

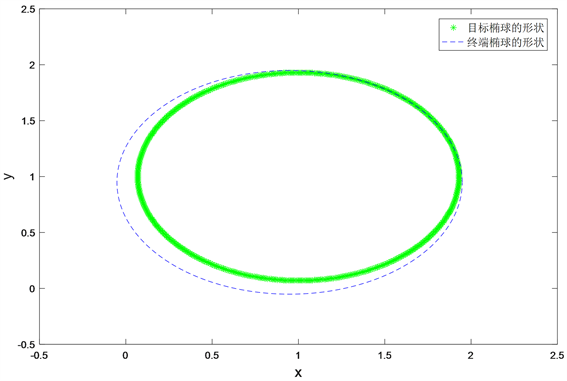
Figure 4. The comparison diagram of the configuration matrix of the terminal ellipsoid and the target ellipsoid with state constraint

图4. 终端椭球和目标椭球形状比较

致谢

首先要感谢我的导师，本文从选题、资料收集到撰写都是在他的亲切关怀和悉心指导下完成的。其次要感谢一直陪伴在我身边的同门以及研究生期间的其他舍友，每当我遇到问题或者烦闷的时候，是她们一直在帮助我。

基金项目

本文由国家自然科学基金面上项目(No. 72171126)支持。