1. 引言
养老保险,即社会基本养老保险的全称,是国家根据一定的法律法规为劳动者达到国家规定的解除劳动义务而设定的工作年龄限制,或为劳动者因年老丧失劳动能力而离职后的基本生活建立的社会保险制度。养老保险是社会保障体系的重要组成部分。2021年5月,国家统计局公布了第七次人口普查数据,其中老年人占比18.7与2010年相比,上升了5.44个百分点。因此,老龄化将在未来十年甚至更长时间内成为常态。随着老龄化的到来,老年人的比例不断增加,养老保险很好地保障了人们退休后的基本生活,从社会形态上来看,养老保险有利于社会稳定。因此,养老保险的研究一直是业界和学术界关注的焦点。一般的养老金主要有DB型养老金和DC型养老金两种。同DB型养老金相比,DC型养老金的缴费率是固定的,并且养老金的给付额是依赖于投资回报率的,所以,被保险人需要承担所有的风险。由于DB型养老金的给付额是提前确定的,并不一定能满足人们退休后的基本生活。所以,DC型养老金成为学者研究的重点。
关于DC型养老金的研究通常是以终端期望效用最大化为目标,进而求得最优投资策略和相应值函数。Yong [1] 考虑了幂效用函数,研究了在CEV模型下DC养老金最优投资问题,通过确立相应的HJB方程求得最优的投资策略。在传统的DC型养老金的研究问题,通常假设风险资产模型满足GBM模型。由于,GBM的波动率和回报率都是固定的不能有效地反映市场的波动性。1976年Cox和Ross [2] 提出了常方差弹性(Constant Elasticity of Variance) CEV模型,与传统的GBM模型相比,该模型得到了进一步扩展。CEV模型的波动率不再是一个常数,它可以有效地反应市场的潜在波动。Xiao et al. [3] 首次将CEV模型引进到养老金优化管理问题中。聂高琴 [4] 在风险资产价格满足CEV模型下,考虑了最大化HARA效用函数下的投资和再保险问题。由于,CEV模型的回报率仍然是常数,其波动率仅与股价有关。1993年Heston [5] 出了风险资产的随机波动率模型,后称Heston模型。同GBM和CEV相比,Heston模型的回报率以及波动率都是随机的,可以更好地去描述金融市场中风险资产价格的变动。林祥和杨益非 [6] 首次在DC型养老金最优问题中假设风险资产的价格满足Heston模型,研究了终端期望效用的最大化问题。Rong et al. [7] 在Heston模型下,研究了投资和再保险问题,推导出了最优投资策略和价值函数。
在传统的DC型养老金优化管理中,通常假设投资者是模糊中性的,也就说对待假定的概率测度是完全信任的。事实上,我们所假定的概率测度只是真实测度的近似。将这种缺乏概率测度而导致的不确定性称为模糊性。为了解决这种模糊性,Anderson et al. [8] 提出了一种鲁棒控制方法,该方法将假定的测度视为参考测度,并考虑一组与参考测度等价的替代测度,研究在替代测度下的最优投资问题。Yi et al. [9] 在风险资产价格满足Heston模型下,研究了稳健的最优投资和再保险问题。Wang和Li [10] 首次将模型的不确定性引入DC型养老金优化模型,考虑了随机利率和随机波动率的影响。在幂效用函数下以终端期望最大化为目标,利用随机动态规划方法,得到了稳健的最优投资策略和相应的价值函数。
DC型养老金作为一项长期的投资项目,在投资期间忽略通货膨胀等背景风险显然是不合适的。Battocchio [11] 首次将通货膨胀引入到DC养老金计划中,在随机工资和通货膨胀两种风险下,以终端期望效用最大化为目标,得到了优化问题的显式解。张笑怡和郭军义 [12] 研究了通货膨胀条件下DC型养老金的均值–方差问题,并且重点分析了价格指数带跳时的最优投资策略。Baltas et al. [13] 研究了通货膨胀率,死亡强度和模型不确定性对DC养老金计划投资策略的影响,在分配阶段对DC型养老金进行了优化管理,并且得到指数效用函数下最优投资策略的显式解。
对于养老金计划持有人,退休后在没有工资收入的前提下主要的经济来源是养老金。所以,他们更在意将退休后收入与退休前工资进行比较。在已有研究DC型养老金优化问题文献中,学者常以养老金账户中财富的终端期望效用最大化为目标。在本文中,我们以工资水平为基准,定义了一个相对财富过程。考虑在模型不确定环境下,风险资产满足Heston模型时,相对财富过程的终端效用最大化问题。在第2、3节我们对所研究模型进行了详细地介绍。在第4节我们提出了相应的鲁棒优化问题。针对幂效用函数,在第5节利用Hamilton-Jacobi-Bellman (HJB)动态规划原理的方法,给出了问题的显示解。在第6节我们给出了一个数值例子,分析了不同参数对最优投资策略的影响。
2. 金融市场
假设金融市场由一个无风险资产和一个风险资产构成,并且是连续开放的、完备的、无摩擦的。定义一个完备的概率空间
,Ω是真实空间,P是概率测度。
是定义在该空间上的标准二维布朗运动,
是该空间上右连续的,由布朗运动
生成的
代数流。
假设t时刻无风险资产
,满足下面微分方程:
(1)
其中短期利率r是一个正常数。
假设t时刻风险资产
,满足下面随机微分方程:
(2)
其中
为常数,
满足下面随机微分方程(CIR模型):
(3)
其中
为正常数,满足
,易知
。假设布朗运动
和
相互独立。
在长期的养老金计划中,投保人会将其工资的固定比例缴纳到养老金账户中,缴纳的额度与投保人所获取的工资成正比,由于投保人的工资是随机的,为了接近实际情况,假设随机工资
满足以下随机微分方程:
(4)
其中,
是一个波动率因子,用来衡量股票风险是如何影响工资的。
通货膨胀一直存在于金融市场中,尤其是受近期疫情的影响。在长期的养老金投资计划中,通货膨胀对资产有着重要的影响,假设通货膨胀
满足下面随机微分方程:
(5)
其中,
表示预期通货膨胀率,
表示波动率因子,并且
,
,即
。考虑通货膨胀下真实的风险资产以及随机工资满足的随机微分方程。
取
(6)
通过伊藤公式(
公式)和乘积法则,可得如下随机微分方程:
(7)
3. 养老金财富过程
假设
是养老金在t时刻的财富值,同时,用于投资到风险资产和无风险资产的比例分别是
,
继续假设交费率
是常数。则养老金的财富过程满足下面的随机微分方程:
(8)
本文研究在通货膨胀下相对财富的鲁棒优化问题,以工资作为基底来定义相对财富,即
。
通过伊藤公式和乘积法则,得到
的随机微分方程
(9)
4. 鲁棒优化问题
在传统的DC型养老金投资问题中,投资者通常被假设是模糊中性的,投资者并不能确切地知道真实的概率测度,我们所知道的概率测度只是真实测度的近似。对于模糊厌恶型投资者的最优投资问题,我们考虑在测度
的参考下,寻找同
等价的测度
,即
。根据Girsanov定理,对于每个和
等价的测度
都存在一个可测的过程
(10)
被称为概率失真过程,使得
(11)
其中
(12)
如果
满足
(13)
那么过程
是一个鞅。
对于每个
(14)
根据Girsanov定理,在替代测度
下
是标准的二维布朗运动。在替代测度
下,对
进行测度转换,可得如下微分方程:
(15)
(16)
(17)
(18)
定义投资策略
,其中
和
分别表示在t时刻投资到风险资产和无风险资产的比例。那么在可替代测度
下,相对财富过程满足下面随机微分方程:
(19)
投资者的目标是通过选择最优投资策略和最优替代测度来最大化相对终端财富效用,我们考虑如下的鲁棒最优投资问题:
(20)
为解决上述问题,定义如下值函数
(21)
其中
和
表示了关于股价动态和股价随机波动率的模糊性。
幂效用函数,如下定义:
(22)
表示模糊厌恶参数。
表示关于股价的模糊厌恶水平,
表示股票波动率的模糊厌恶水平。
我们称
为可允许策略,如果满足下面条件:
1) 对任意的
,
关于
循序可测;
2)
;
3) 对于任意的
等式(19)有唯一的解
并且
(23)
5. 最优化问题的解
假设投资者具有幂效用函数
,其中
为常相对风险厌恶系数,为了计算方便,定义
即w关于t一阶连续可导,w关于
二阶连续可导。
定义一个Hamitonian算子
(24)
其中
是对其相应变量的偏导。
根据随机控制动态规划理论,可推出值函数满足如下HJB方程:
(25)
假设
是方程的解,由一阶最优条件可知
分别为:
(26)
(27)
将等式(26)、(27)带入HJB方程中,有
(28)
由的
一阶微分条件,可知
(29)
将
带入等式(28),有
(30)
推测等式(30)有以下形式的解
(31)
且满足
。
上式关于变量求一阶和二阶偏导
(32)
将J及其偏导数代等式(30),可知
(33)
为求解等式(33),假设
(34)
且满足
,将函数g关于
求偏导,我们得到
(35)
将等式(34)、(35)带入等式(33)可得
(36)
分析上式等式可得
(37)
分析等式(37)可知
(38)
根据相应的边界条件求解上述方程,可得
(39)
其中
(40)
由于 ,则有
,则有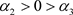 ,因此
。
,因此
。
总结以上结果,根据Kraft [14] 书中推论1.2和Bayraktar和Zhang [15] 定理6.1,得到如下验证定理:
当模型参数满足一定条件时,鲁棒最优投资模型在幂效用函数下的值函数
等于函数
(41)
相应最优投资策略为:
(42)
最坏情形的测度为:
(43)
(44)
其中
由等式(39)给出。
6. 数值分析
在数值算例中,我们考虑在通货膨胀下幂效用函数模糊厌恶系数
,风险厌恶参数
,缴费率
,波动率因子
,预期收益率
和投资期限T对投资策略的影响。为方便数值模拟假设
是恒定的。
具体参数取值如下(表1)。

Table 1. Numerical simulation parameters
表1. 数值模拟参数表

Figure 1. The influence of fuzzy aversion parameter
, risk aversion coefficient
and investment period T on optimal investment proportion
图1. 模糊厌恶参数
,风险厌恶参数
和投资期限T对最优投资比例的影响
图1显示了模糊厌恶参数
和风险厌恶
对最优投资比例的影响。随着参数
和
增加,股票的投资比例不断降低。当
增加时,基金管理者对股票动态更加模糊,因此养老金管理者会降低股票的投资比例。当
增加时,基金管理者变得更加风险厌恶,因此管理者更加愿意接受风险较低的投资。当投资期限T加长时,基金管理者会在风险资产上投入更多的财富来获取更高的利益。
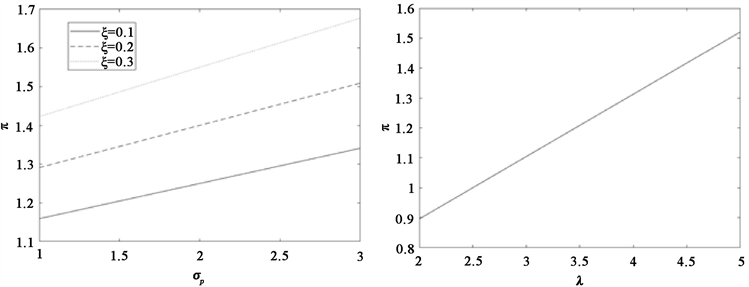
Figure 2. The influence of payment rate
, inflation volatility
and expected rate of return
on optimal investment proportion
图2. 缴费率
,通货膨胀波动率
和预期收益率
对最优投资比例的影响
图2显示了交费率
,通货膨胀波动率
和预期收益率
对最优投资比例的影响。随着参数
,
和
的增加,股票的投资比例不断增加。当缴费率
增大时,养老金的缴纳比例增加,养老金账户中的资产增加,使得基金管理者更倾向于高风险的资产来获取高收益。当
增加时,通货膨胀波动率增加,通货膨胀增加对养老金资产具有腐蚀性,因此基金管理者会加大对股票的投资来获取更高的收益来对冲通货膨胀带来的腐蚀性。当
增加时,表示养老金投资到股票的收益率在更加,养老金账户中有更多的资产,所以基金管理者为了获得更高的收入,会加大对股票的投资。
7. 本文总结
本文考虑了通货膨胀下DC型养老金的鲁棒优化问题,其中养老金被投资到无风险资产和风险资产中,同时为了接近实际情况,本文假设随机工资和风险资产价格满足Heston模型,通过Girsanov定理和随机动态理论确立相对财富的随机微分方程和对应的HJB方程,推导出幂效用函数下最优投资策略和值函数,最后通过MATLAB分析模糊厌恶系数
,风险厌恶参数
,缴费率
,波动率因子
,预期收益率
和投资期限T对最优投资策略的影响。