高维线性模型中参数组的显著性检验

Significance Tests for Parameter Group in High-Dimensional Linear Models

摘要: 高维线性模型中参数的显著性检验是统计学研究的热点。现有的统计方法往往局限于参数的稀疏性假设，但在实际中，该假设是很难检验且极容易被违反的。本文通过重构回归对参数组进行显著性检验，首先利用原假设的结构得到重构回归模型，并建立设计矩阵间的线性相关模型，进而计算两模型误差的相关性，以此将待测原假设转化为可检验的矩条件，并建立检验统计量，得到检验统计量的渐近分布。最后，通过模拟试验，观察该检验方法在不同的误差和设计矩阵设置下的第I类错误概率和势函数曲线。试验结果表明：对于参数组检验，矩方法能保证第I类错误概率控制在显著性水平附近，并且可以证明检验的势特征。

Abstract: The significance test of parameters in high-dimensional linear models is a hot topic in statistical re-search. Existing statistical methods are often limited to the assumption of parameter sparsity, but in practice, this assumption is difficult to test and easily violated. In this paper, the significance test of the parameter group is carried out through reconstruction regression. First, the reconstruction regression model is obtained by using the structure of the null hypothesis, and the linear correla-tion model between the design matrices is established, and then the correlation between the errors of the two models is calculated. The hypothesis is transformed into a testable moment condition, establish the test statistic, and obtain the asymptotic distribution of the test statistic. Finally, through simulation experiments, the probability of Type I error of the test method and power func-tion curve under different error and design matrix settings are observed. The experimental results show that for the parameter group test, the moment method can ensure that the probability of Type I error is close to the significance level, and can prove the power property of the test.

1. 引言

信息技术的快速发展造成了数据收集和数据分析的重大变革。现如今，不同领域的科学研究越来越依赖高维观测数据，即数据维度p远大于样本容量n。大量高维数据的建模、推断和预测逐渐成为统计学研究的热点。另外，由于数据维度和科技水平的限制，现有的方法通常假设参数的稀疏性，即参数向量中非零元素的个数s满足：当 $n\to \infty$ 时， $s/n\to 0$ [1]。常见的惩罚方法包括Lasso [2]、Dantzig Selector [3]、square root Lasso [4] 和岭估计 [5]。这些方法已经被广泛研究，而且惩罚方法已经应用于诸多领域，例如生物成象、疾病跟踪、政策制定及营销策略等。

假设检验在统计理论和应用中扮演着重要的作用。假设检验的现有方法往往局限在参数的超稀疏领域，即 $s=o\left(\sqrt{n}/\log p\right)$。 [6] 中研究了具有随机设计的高维线性回归模型的置信区间，并分析了置信区间的期望长度及其在不同稀疏水平下的自适应性； [7] 中提出了一种偏差校正方法，证明了低维投影是一种构造置信区间和假设检验的有效方法； [8] 在稀疏水平 $s=\frac{n}{{\log }^{2}p}$ 下，提出了一种纠偏Lasso估计，并证明了其渐近正态性； [9] 中将参数向量的单分量或低维分量估计推广到广义线性模型； [10] 在稀疏模型下提供了有效控制第I类错误概率的方法； [11] 在高维线性模型的框架下构造了去偏估计量，并建立其渐近正态性； [12] 考虑了高维稀疏逻辑回归模型的预测，通过方差–偏差均衡思想，提出了一种新的偏差校正估计方法； [13] 考虑了单样本及双样本回归条件下回归系数的全局检验和多重检验，利用偏差校正的广义低维投影构造了检验全局参数的检验统计量，并导出其渐近原分布； [14] 定义了一种新的去偏阈值岭回归方法，并证明了一致性结果和高斯近似定理； [15] 基于 $L^2$ 范数建立检验统计量，用于检验高维平均向量是否等于0，并表明在正则性条件下，其渐近原分布与 ${\chi }^2$ 混合的极限分布相同。以上推理方法都假设了模型的稀疏性，但是现有的推理方法对稀疏性假设很敏感，一旦违背该假设，可能会失去对第I类错误概率的控制。为了摆脱稀疏性假设， [16] 提出了近似稀疏的CorrT检验，通过重构回归将原假设转化为可检验的矩条件； [17] 将矩方法推广到全高斯设计下回归参数线性泛函的假设检验。

上述文献考虑的是单参数分量或全局参数，但据我们所知，目前对非稀疏参数组的假设检验研究甚少。在全基因组基因表达谱研究领域， $\beta \in {\Re }^p$ 代表整个基因组，但是我们感兴趣的往往是与某一性状有关的基因组，因此参数组的假设检验问题具有非常重要的应用价值。设 ${\beta }_G\subseteq \beta$ 是我们感兴趣的参数组，则本文要研究以下假设检验问题：

$H_0:{\beta }_G={\beta }_G^0\text{v}\text{.s}.H_1:{\beta }_G\ne {\beta }_G^0$。

结合上述文献中的方法和应用场景，根据原假设结构，首先重构原始线性模型，然后建立两个设计矩阵的相关模型，进而计算两模型误差间的相关关系，以此将原假设转化为可检验的矩条件，估计矩条件中的未知参数，并构造检验统计量，推导其渐近分布。此过程在不施加任何稀疏性假设的情况下，保证了检验的第I类和第II类错误概率。

本文的剩余部分组织如下：在第2节中，我们利用矩方法对参数组进行显著性检验，将原假设转换为可检验的矩条件，并提出检验统计量及渐近分布；在第3节中，我们通过模拟试验验证了所提检验方法在不同的设计矩阵和误差设置下的第I类和第II类错误概率；在第4节中，进行了总结和讨论。

2. 参数组的显著性检验

在本节中，我们提出了高维线性模型中参数组的显著性检验方法。首先，利用原假设的结构，重构高维线性回归模型，并建立该模型中的两组设计矩阵的线性相关模型，计算重构回归模型及线性相关模型中的两误差的矩条件，以此将原假设转化为可检验的矩条件；然后，利用Lasso方法估计矩条件中的未知参数；最后，建立检验统计量，并推导其渐近分布，并利用模拟的方法得到检验的临界值。

2.1. 符号说明

我们首先定义下面的符号。对于一个向量 $v\in {\Re }^k$， ${\Vert v\Vert }_{\infty }=\underset{1\le i\le k}{\max }\left|v_i\right|$， ${\Vert v\Vert }_0={\displaystyle \underset{i=1}{\overset{k}{\sum }}I\left(v_i\ne 0\right)}$，其中 $I(\cdot )$ 表示示性函数。 $v_G$ 表示由 $v_j,j\in G$ 组成的子向量， $v_{-G}$ 表示由 $v_j,j\in G^c$ 组成的子向量。对于矩阵A， $a_i$ 表示该矩阵的第i行， $A_j$ 表示其第j列。 $A_G$ 表示由向量 $A_j,j\in G$ 构成的子矩阵， $A_{-G}$ 表示由向量 $A_j,j\in G^c$ 构成的子矩阵， ${\Vert A\Vert }_{\infty }=\max \left|A_{i,j}\right|$。对于两个序列 $a_n,b_n>0$， $a_n\approx b_n$ 表示存在常数 $C_1,C_2>0$，使得对于任意n， $a_n\le C_1{b}_n$ 且 $b_n\le C_2{a}_n$。

2.2. 重构回归模型

对于高维线性模型：

$y_i=x_i^{\text{T}}\beta +{\epsilon }_i\text{,}i=1,2,\cdots ,n$， (1)

其中， $y_i$ 是响应变量， $x_i\in {\Re }^p$ 是解释向量，其满足 $x_i~N\left(0,\Sigma \right)$，其中 $\Sigma$ 是一个未知协方差矩阵。误差向量 $\epsilon \in {\Re }^n$ 和设计矩阵 $X={\left(x_1^{\text{T}},x_2^{\text{T}},\cdots ,x_n^{\text{T}}\right)}^{\text{T}}$ 是不相关的，且满足 $E\left({\epsilon }_i\right)=0$， $Var\left({\epsilon }_i\right)={\sigma }_{\epsilon }^2$， $0<{\sigma }_{\epsilon }<\infty$。参数向量 $\beta \in {\Re }^p$ 是未知的，在上述模型中，我们允许 $p\gg n$。

本文的目的是对参数组进行假设检验，即：

$H_0:{\beta }_G={\beta }_G^0\text{v}\text{.s}.H_1:{\beta }_G\ne {\beta }_G^0$， (2)

其中，子向量 $G\subseteq \left\{1,2,\cdots ,p\right\}$，且 ${\beta }_G\in {\Re }^k$ 是我们感兴趣的参数组， ${\beta }_G^0$ 是给定参数组。根据待测原假设，我们将参数向量分解为 $\beta ={\left({\beta }_G^{\text{T}},{\beta }_{-G}^{\text{T}}\right)}^{\text{T}}\in {\Re }^P$，此时可将模型(1)重写为：

$y=z^{\text{T}}{\beta }_G+w^{\text{T}}{\beta }_{-G}+\epsilon$， (3)

其中， $z=x_G\in {\Re }^k$， $w=x_{-G}\in {\Re }^{p-k}$。

为了检验原假设，(2)式两端同时减 $z^{\text{T}}{\beta }_G^0$，得到

$y-z^{\text{T}}{\beta }_G^0=z^{\text{T}}\left({\beta }_G-{\beta }_G^0\right)+w^{\text{T}}{\beta }_{-G}+\epsilon$。

上式中，包含原假设 $H_0:{\beta }_G-{\beta }_G^0=0$。令 $v=y-z^{\text{T}}{\beta }_G^0$， $e=z^{\text{T}}\left({\beta }_G-{\beta }_G^0\right)+\epsilon$，得到如下重构回归模型：

$v=w^{\text{T}}{\beta }_{-G}+e$。 (4)

在此模型中，当原假设成立时， $E\left(ew\right)=E\left(\epsilon w\right)=E\left(\epsilon \right)E\left(w\right)=0$。否则，

$E\left(ew\right)=E\left[\left(z^{\text{T}}\left({\beta }_G-{\beta }_G^0\right)+\epsilon \right)w\right]=E\left[z^{\text{T}}\left({\beta }_G-{\beta }_G^0\right)w\right]={\left({\beta }_G-{\beta }_G^0\right)}^{\text{T}}E\left(z{w}^{\text{T}}\right)$。

由于z和w之间可能存在线性相关性，故 $E\left(z{w}^{\text{T}}\right)$ 不一定为0。下面我们建立z和w之间线性相关模型：

$z={\Pi }^{\text{T}}w+u$， (5)

其中， $\Pi \in {\Re }^{\left(p-k\right)\times k}$ 是相关系数矩阵， $u\in {\Re }^k$ 是误差项，且本文假设u和w是独立的，且u服从高斯分布，满足 $E\left(u\right)=0$。在本文中，我们合理假设 $\Pi$ 的列稀疏性，实际上， $\Pi$ 的列稀疏性假设表明了精度矩阵 ${\Omega }_X={\Sigma }_X^{-1}$ 的稀疏性。

考虑(4)中的伪误差e和(5)中的误差u之间的相关性，建立以下矩条件：

$E\left(ue\right)=E\left[u\left(z^{\text{T}}\left({\beta }_G-{\beta }_G^0\right)+\epsilon \right)\right]=E\left(u{u}^{\text{T}}\right)\left({\beta }_G-{\beta }_G^0\right)$， (6)

在(2)中的原假设下， $E\left(ue\right)=0$ ；否则， $E\left(ue\right)\ne 0$。因此，(2)中的检验问题等价于检验：

$H_0:E\left[\left(z-{\Pi }^{\text{T}}w\right)\left(v-w^{\text{T}}{\beta }_{-G}\right)\right]=0\text{v}\text{.s}\text{.}{H}_1:E\left[\left(z-{\Pi }^{\text{T}}w\right)\left(v-w^{\text{T}}{\beta }_{-G}\right)\right]\ne 0$， (7)

其中， $\Pi$ 和 ${\beta }_{-G}$ 是未知的待估参数。根据 $\Pi$ 的列稀疏性，容易获得其一致估计 $\hat{\Pi }$，此时，对于 ${\beta }_{-G}$ 的任意估计 ${\tilde{\beta }}_{-G}$，我们有：

$E\left[\left(z-{\hat{\Pi }}^{\text{T}}w\right)\left(v-w^{\text{T}}{\tilde{\beta }}_{-G}\right)\right]\to E\left[\left(z-{\Pi }^{\text{T}}w\right)\left(v-w^{\text{T}}{\tilde{\beta }}_{-G}\right)\right]=E\left(ue\right)$。

因此，上述内积结构不依赖对 ${\beta }_{-G}$ 的良好估计的需要。

2.3. 参数估计

(7)中含有未知参数 $\Pi$ 和 ${\beta }_{-G}$，我们建立它们的Lasso估计。对于设计矩阵 $X={\left(x_1^{\text{T}},x_2^{\text{T}},\cdots ,x_n^{\text{T}}\right)}^{\text{T}}\in {\Re }^{n\times p}$，我们定义新的响应向量 $V=Y-Z{\beta }_G^0\in {\Re }^n$，新的设计矩阵 $Z=X_G\in {\Re }^k$， $W=X_{-G}\in {\Re }^{p-k}$，且 $e=Z\left({\beta }_G-{\beta }_G^0\right)+\epsilon ={\left(e_1,e_2,\cdots ,e_n\right)}^{\text{T}}\in {\Re }^n$。 ${\beta }_{-G}$ 的Lasso估计为：

${\hat{\beta }}_{-G}=\arg {\min }_{{\beta }_{-G}\in {\Re }^{p-k}}\left\{{\Vert V-W{\beta }_{-G}\Vert }_2^2+{\lambda }_1{\Vert {\beta }_{-G}\Vert }_1\right\}$， (8)

其中，参数 ${\lambda }_1$ 满足 ${\lambda }_1\approx \sqrt{n^{-1}\log p}$。 ${\Pi }_j$ 的Lasso估计为：

${\hat{\Pi }}_j=\arg {\min }_{{\Pi }_j\in {\Re }^{p-5}}\left\{{\Vert Z_j-W{\Pi }_j\Vert }_2^2+{\lambda }_2{\Vert {\Pi }_j\Vert }_1\right\},j\in G$， (9)

其中， ${\lambda }_2\approx \sqrt{n^{-1}\log p}$。 $\Pi$ 的Lasso估计为：

$\hat{\Pi }=\left({\hat{\Pi }}_j,j\in G\right)\in {\Re }^{\left(p-k\right)\times k}$。 (10)

2.4. 检验统计量

在本小节中，对于(7)中的假设问题，我们用 ${\hat{\beta }}_{-G}$ 和 $\hat{\Pi }$ 构造检验统计量，并用模拟的方法获得检验的临界值。

通过插入(8)和(10)中的估计值，我们构造如下检验统计量：

$T_n=n^{-1/2}{\hat{\sigma }}_e^{-1}{\Vert {\left(Z-W\hat{\Pi }\right)}^{\text{T}}\left(V-W{\hat{\beta }}_{-G}\right)\Vert }_{\infty }$， (11)

其中， ${\hat{\sigma }}_e=\frac{{\Vert V-W{\hat{\beta }}_{-G}\Vert }_2}{\sqrt{n}}$。当原假设成立时， $T_n$ 的值接近为0；反之， $T_n$ 的值较大。因此，当 $T_n$ 的值大于某临界值时，应该拒绝原假设。

在(7)中的原假设下，

$n^{-1/2}{\hat{\sigma }}_e^{-1}{\left(Z-W\hat{\Pi }\right)}^{\text{T}}\left(V-W{\hat{\beta }}_{-G}\right)=n^{-1/2}{\hat{\sigma }}_e^{-1}{\left(\Pi -\hat{\Pi }\right)}^{\text{T}}{W}^{\text{T}}\hat{e}+n^{-1/2}{\hat{\sigma }}_e^{-1}{U}^{\text{T}}\hat{e}$。

注意，我们构造的U独立于 $\left(V,W\right)$，但是 ${\hat{\beta }}_{-G}$ 只与 $\left(V,W\right)$ 有关，因此 $\hat{e}=V-W{\hat{\beta }}_{-G}$ 也完全依赖于 $\left(V,W\right)$，故U和 $\hat{e}$ 是不相关的。设 ${\delta }_n$ 是一个由 $\left(V,W\right)$ 生成的 $\sigma$ -代数，则

$E\left(n^{-1/2}{\hat{\sigma }}_e^{-1}{\left(\Pi -\hat{\Pi }\right)}^{\text{T}}{W}^{\text{T}}\hat{e}+n^{-1/2}{\hat{\sigma }}_e^{-1}{U}^{\text{T}}\hat{e}|{\delta }_n\right)\to 0$，

$Var\left(n^{-1/2}{\hat{\sigma }}_e^{-1}{\hat{U}}^{\text{T}}\hat{e}\right)=n^{-1}{\hat{\sigma }}_e^{-2}Var\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{\hat{U}}_{i,G}^T{\hat{e}}_i}\right)=Q$，

其中，Q是一个分块对角矩阵，其中每一个对角块为 $q=n^{-1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\hat{\sigma }}_e^{-2}{\hat{e}}_i{}^{2}E\left({\hat{u}}_i{\hat{u}}_i^{\text{T}}\right)}=E\left({\hat{u}}_1{\hat{u}}_1^{\text{T}}\right)=n^{-1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\hat{u}}_i{\hat{u}}_i^{\text{T}}}$，其中 ${\hat{u}}_i^{\text{T}}$ 是 $\hat{U}$ 的第i行。因此，可以得到在 ${\delta }_n$ 下， ${\Vert n^{-1}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{u}_i{\hat{e}}_i{\hat{\sigma }}_e^{-1}}\Vert }_{\infty }$ 与 ${\Vert \xi \Vert }_{\infty }$ 的分布渐近相同，其中 $\xi ~N\left(0,q\right)$。我们引入函数 $\Gamma \left(x,A\right):=P\left({\Vert \xi \Vert }_{\infty }\le x\right)$，其中 $\xi ~N\left(0,A\right)$，则 $\Gamma \left(x,q\right)$ 与 $T_n$ 的分布渐近相等，而且 $\Gamma \left(x,q\right)$ 可以通过模拟实现。

3. 仿真试验

我们将通过仿真试验展示所提方法的有限样本属性。不失一般性，我们检验 $\beta$ 的前5个分量：

$H_0:{\beta }_G={\beta }_G^0$，

其中 $G=\left\{1,2,3,4,5\right\}$。

在所有的模拟试验中，我们设置 $n=200$， $p=500$，检验的名义水平为 $\alpha =0.05$。拒绝概率是基于100次重复试验得到的，并设置参数 ${\lambda }_1={\lambda }_2=0.5\sqrt{n^{-1}\log p}$，这是一个常用的选择，我们在以下的模拟中也证明了该选择可提供良好的结果。

3.1. 试验设置

我们在以下3种不同高斯设计下证明试验结果：

在这种情况下，我们考虑标准的Toeplitz设计矩阵，即X各行独立同分布地取自 $N\left(0,{\Sigma }_1\right)$，其中 ${\left({\Sigma }_1\right)}_{i,j}={0.4}^{\left|i-j\right|}$。

在此情况下，我们考虑不相关设计矩阵，其中X各行独立同分布地取自 $N\left(0,{\Sigma }_2\right)$，且

${\Sigma }_2=\{\begin{array}{l}1,i=j\\ 0,i\ne j\end{array}$。

在此情况下，我们考虑等相关设计矩阵，即X各行独立同分布地取自 $N\left(0,{\Sigma }_3\right)$，且

${\Sigma }_3=\{\begin{array}{l}1,i=j\\ 0.4,i\ne j\end{array}$。

除此之外，我们考虑两种不同的误差分布：

轻尾误差分布，在此情况下，误差 $\epsilon$ 取自标准正态分布；

重尾分布，在此情况下， $\epsilon$ 取自自由度为3的t-分布。

设 $s={\Vert \beta \Vert }_0$ 表示模型稀疏性，即 $\beta$ 中非零元素的个数，并设置从 $s=3$ (超稀疏)到 $s=p$ (稠密)。对于稀疏度s，我们设置模型参数为：

${\beta }_j=\{\begin{array}{l}\frac{3}{\sqrt{s}},1\le j\le s\\ 0,j>s\end{array}$。

为了说明本文所示的矩方法的鲁棒性，我们还将我们的矩方法与 [9] 中提出的用纠偏Lasso估计构造Wald检验的方法(WL)进行比较。矩方法的第I类错误概率计算如下：

$P=\frac{num\left(I\left(T_n>{\Gamma }^{-1}\left(1-\alpha ,q\right)|H_0\right)\right)}{Num}$，

即在所有的试验中，原假设成立时拒绝原假设的试验所占比例，其中 $Num=100$。WL的具体实现过程为：首先计算参数 $\beta$ 的纠偏估计 ${\hat{\beta }}_{debias}$ 以及精度矩阵的nodewise Lasso估计 ${\hat{\Theta }}_{Lasso}$，当且仅当

$\underset{j\in G}{\max }\frac{\sqrt{n}\left|{\hat{\beta }}_{debias,j}-{\beta }_j^0\right|}{{\sigma }_{\epsilon }\sqrt{{\hat{\Omega }}_{j,j}}}>{\Psi }^{-1}\left(1-\alpha \right)$，

拒绝原假设，其中， $\Psi =\underset{j\in G}{\max }\frac{\left|W_j\right|}{{\sigma }_{\epsilon }\sqrt{{\hat{\Omega }}_{j,j}}}$，且 $W={\hat{\Theta }}_{Lasso}{X}^{\text{T}}\epsilon /\sqrt{n}~N\left(0,{\sigma }_{\epsilon }^2\hat{\Omega }\right)$， $\hat{\Omega }=\hat{\Theta }\hat{\Sigma }{\hat{\Theta }}^{\text{T}}$， $\hat{\Sigma }=X^{\text{T}}X/n$。且Wald检验的第I类错误概率计算如下：

$p=num\left(I\left(\underset{j\in G}{\max }\frac{\sqrt{n}\left|{\hat{\beta }}_{debias,j}-{\beta }_j^0\right|}{{\sigma }_{\epsilon }\sqrt{{\hat{\Omega }}_{j,j}}}>{\Psi }^{-1}\left(1-\alpha \right)|H_0\right)\right)/Num$。

3.2. 试验结果及分析

3.2.1. 第I类错误概率

我们将轻尾误差下的第I类错误结果收集在表1中，其中包括轻尾误差联合Toeplitz设计矩阵，轻尾误差联合不相关设计矩阵，该表的每一行代表 $\beta$ 的不同稀疏性水平，在以上设置下，我们考虑矩检验和Wald检验的第I类错误。

Table 1. The Type I errors of moment method and Wald test under light-tailed error settings

表1. 轻尾误差设置下矩方法和Wald检验的第I类错误

从上表容易看出，在表1的两种设置下，矩方法在不同的稀疏水平下的第I类错误概率始终维持在名义水平0.05左右，即使 $s=p$，即稠密模型，矩方法的第I类错误概率仍然保持稳定，这说明矩方法对设计矩阵和模型稀疏性具有鲁棒性。相反，对于Wald检验，在超稀疏水平( $s=3$ 和 $s=5$ )上，轻尾误差分布联合不相关矩阵设置下的第I类错误概率可以控制在0.05左右，但是轻尾误差分布联合Toeplitz设计下的第I类错误概率远高于名义水平0.05，且随着稀疏水平不断增加，检验的第I类错误概率不断提高，甚至达到0.9左右，这说明Wald检验对于设计矩阵设置不具备鲁棒性，对于稀疏模型，无法控制第I类错误概率，而对于稠密模型( $s=p$ )，第I类错误概率高达0.9左右，检验完全失效。

我们将重尾误差下的第I类错误概率结果收集在表2中，其中包括重尾误差联合Toeplitz设计矩阵，重尾误差联合不相关设计矩阵及重尾误差联合等相关设计矩阵，该表的每一行代表 $\beta$ 的不同稀疏性水平，在以上设置下，我们考虑矩检验和Wald检验的第I类错误概率。

Table 2. The Type I errors of moment method and Wald test under heavy-tailed error settings

表2. 重尾误差设置下矩方法和Wald检验的第I类错误

从表2可以看出，在重尾误差联合不同的设计矩阵设置下，随着模型的稀疏水平不断增加，矩方法的第I类错误概率仍然维持在显著性水平0.05左右，这说明对于重尾误差分布，矩方法对设计矩阵和稀疏水平设置仍然具有鲁棒性，第I类错误概率始终保持稳定。对于Wald检验，即使在稀疏水平下，检验的第I类错误概率就高达0.9左右，这说明Wald检验对于重尾误差分布设置完全失效。

综上，对于矩方法，无论是轻尾误差分布，还是重尾误差分布，矩方法对于设计矩阵及稀疏水平设置都具有鲁棒性，这说明矩方法的第I类错误概率具有稳定性。与之相反，Wald检验在轻尾误差分布下，随着稀疏水平的增加，第I类错误概率逐渐提高，并在稠密模型中，该概率高达0.9；而在重尾误差分布下，即使对于稀疏模型，第I类错误概率已高达0.9，这说明Wald检验误差分布不具有鲁棒性，难以控制第I类错误概率。

3.2.2. 势特征

为了观察检验的势特征，我们通过以下检验问题观察势特征：

$H_0:{\beta }_G={\beta }_G^0\text{v}\text{.s}\text{.}{H}_1:{\beta }_G={\beta }_G^0+H$，

其中， $G=\left\{1,2,3,4,5\right\}$，且我们设置H为 $H=\left(h,0,0,0,0\right)$，h是一给定常数，其衡量了与原假设的距离。注意， $h=0$ 表示原假设成立。矩方法检验的势计算如下：

$power=\frac{num\left(I\left(T_n>{\Gamma }^{-1}\left(1-\alpha ,\hat{Q}\right)|H_1\right)\right)}{Num}$，

即在所有的试验中，原假设不成立时拒绝原假设的试验所占比例，其中 $Num=100$。WL的势计算如下：

$power=num\left(I\left(\underset{j\in G}{\max }\frac{\sqrt{n}\left|{\hat{\beta }}_{debias,j}-{\beta }_j^0\right|}{{\sigma }_{\epsilon }\sqrt{{\hat{\Omega }}_{j,j}}}>{\Psi }^{-1}\left(1-\alpha \right)|H_1\right)\right)/Num$，

为了验证本文所用的矩方法在稠密模型下参数组检验中的优良性质，我们仅考虑 $s=p$ 时的势函数。通过设置不同的h值，首先得到如下轻尾误差分布下的势函数曲线：

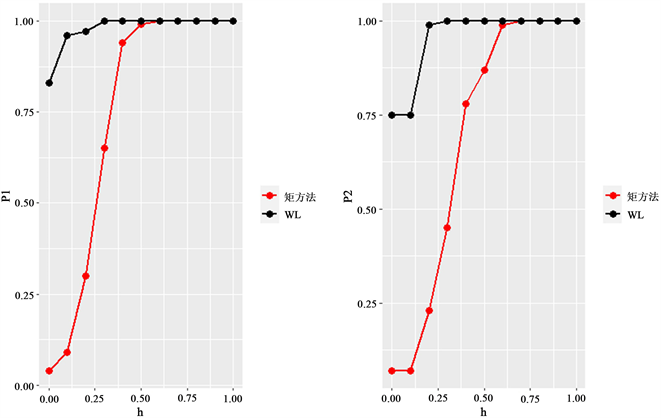
Figure 1. Power function curve under light-tailed error distribution

图1. 轻尾误差分布下的势函数曲线

图1中左侧表示的是轻尾误差分布联合Toeplitz设计矩阵，右侧表示轻尾误差分布联合不相关设计矩阵，其中红色的线表示本文所利用的矩方法，黑色的线表示Wald检验，最左侧 $h=0$ 的点表示第I类错误概率，其余点表示h取不同值时检验的势。从上图可以看出，在轻尾误差分布设置中，矩方法的第I类错误概率均在名义水平0.05左右，且以很快的速度达到1，这说明利用矩方法进行显著性检验时，该检验具有势属性，并且在原假设与备择假设距离较小时，就足以分离原假设和备择假设；反之，对于Wald检验，从图中可以看出，其势函数以更快的速度达到1，但是当 $h=0$，即原假设成立时，该检验的第I类错误概率显著地大于名义水平0.05，且不相关设计下的第I类错误概率略大于Toeplitz设计矩阵下的第I类错误概率。我们将重尾误差分布下的势函数曲线绘制在如下图2中。

图2中最左侧图表示重尾误差分布联合Toeplitz设计矩阵，中间表示重尾误差分布联合不相关设计矩阵，右侧表示重尾误差分布联合等相关设计矩阵，其中红色的线表示矩方法，黑色的线表示Wald检验，最左侧 $h=0$ 的点表示第I类错误概率，其余点表示h取不同值时检验的势。从图中可以看出，在3种不同的设计矩阵下，矩检验的第I类错误概率均在名义水平0.05左右，其势以一定的速度达到1，其中Toeplitz设计矩阵下，矩检验的势达到1的速度最快，当 $h=10$ 时，检验的势已达到0.93；不相关设计矩阵下的矩检验的势达到1的速度次之，当 $h=15$ 时，检验的势已达到0.98；不相关设计矩阵下的矩检验的势达到1的速度最慢，当 $h=25$ 时，检验的势已达到0.95。而对于重尾误差分布下的Wald检验，其势一直维持在1，但是当 $h=0$，即原假设成立时，该检验的第I类错误概率也几乎达到1，这说明该设置下的Wald检验完全失效。

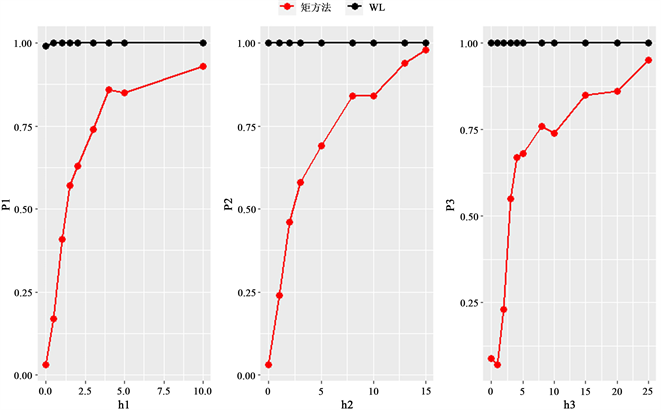
Figure 2. Power function curve under heavy-tailed error distribution

图2. 重尾误差分布下的势函数曲线

4. 总结和讨论

在本文中，我们利用矩方法对参数组进行显著性检验。首先根据原假设的结构，重构回归模型，并建立该模型中两个设计矩阵的线性相关模型，通过建立以上两模型中误差的矩条件得到原假设的等价检验，该矩条件的建立放宽了对非稀疏参数良好估计的需求，并且不依赖任何非稀疏假设。仿真试验表明，在不同的误差分布和设计矩阵设置下，矩方法的第I类错误概率能稳定维持在显著性水平 $\alpha$ 左右，势曲线很快达到1；与之相反，由于现有的参数估计方法大多依赖于稀疏性假设，因此对于稠密模型，往往难以控制第I类错误概率。除此之外通过建立参数估计的渐近分布的检验，对设计矩阵及误差分布不具有鲁棒性。