1. 引言
对结构进行损伤识别,通常先判断结构是否存在损伤,进而确定损伤位置以及损伤程度 [1]。土木工程领域常通过结构的动力响应获取频率与振型进行损伤识别。基于模态参数的损伤识别方法在实际应用中,可能存在频谱泄露、截断误差以及丢失原始信号中的时域信息等问题。在时域提取振动响应信号中对结构损伤敏感的特征信息,省去了信号变换和模态识别的过程。阳洋 [2] 等基于统计矩理论,利用结构加速度响应在时域内构建八阶矩作为损伤指标,该方法可直接通过响应快速判断结构是否存在损伤以及损伤的位置。雷家艳 [3]、Li [4] [5] 等利用结构响应的自/互相关函数、协方差构造损伤识别因子进行结构损伤判定。
通过振动信号分析判断结构是否损伤,分析对象多是加速度响应。结构损伤的出现会引起损伤位置处应力重分布,应力的大小是由应变反映的。相较加速度,应变更能敏感地反映结构局部刚度的变化。本文提出一种基于应变二次协方差矩阵元素(QCoS)的结构损伤识别方法,推导证明了结构在冲击荷载作用下,应变二次协方差矩阵元素是结构频率、应变模态振型、阻尼等结构模态参数的函数。利用结构应变二次协方差矩阵元素构建损伤特征向量,通过向量置信度准则以及特征向量改变量实现结构损伤的判定和损伤的定位。通过简支钢梁的数值算例,分析结构局部不同程度的损伤对QCoS的影响,验证了该损伤识别方法的有效性。
2. 基本理论
2.1. 应变二次协方差
下式为N个自由度系统的随机运动方程,
(1)
式中M、C、K分别是N × N的质量、阻尼和刚度矩阵,
、
和
分别是N × 1的加速度、速度和位移向量,L是N × 1的映射向量,
是将激励
作用于系统的某自由度。
经作者推导自由度l的应变单位脉冲响应函数如公式(2),推导过程见文献 [6],
(2)
上式中,
,
和
分别是第i阶无阻尼模态频率、有阻尼模态频率和阻尼比,
是第i阶应变模态振型的第l个元素,
在
作用下,自由度l的应变响应可表达为 [7],
(3)
若激励
为冲击荷载作用,可近似认为
,
是脉冲激励。自由度l的响应
与自由度p的响应
之间的互相关函数可通过下式计算得到,
(4)
将式(2)代入式(4)得到
(5)
式中,
,
响应的互相关函数也可表示为
(6)
式中,
由下式计算得到应变响应的二次协方差(QCoS)矩阵,
(7)
式中,
,
自由度p,l在实际结构测试中对应应变响应测点p,lg,(g = 0, 1, 2, ∙∙∙, nst),nst为应变测点数。两测点p,lg数据构成的Rplg是以p为参考点的应变响应互相关函数。当p = lg时,Rplg就是自相关函数。式中
,
为测试采样时间间隔。
矩阵
的第i行第j列元素可由下式计算得到,
(8)
式(8)所示,结构应变响应二次协方差矩阵Q的元素仅与结构的频率、振型、阻尼比等模态参数有关。结构的损伤会引起结构模态参数的改变,导致Q矩阵元素发生变化。因此,矩阵元素可作为损伤特征参数。
在实际测试当中,各测点响应是一系列离散的时间序列,积分式(4)可由有限求和式替代。对于样本数是ns的时间序列,τ为时间延迟,离散数据的互相关函数可表示成:
(9)
将由式(9)求得的Rplg代入式(7)即可得到结构应变响应的二次协方差矩阵Q。矩阵的行数r、列数c即对应测点lr和测点lc,(r, c = 1, 2, ∙∙∙, g),第r行、c列的矩阵元素QCoS,即Qrc由下式可得,
(10)
2.2. 向量置信度准则
采用模式识别方法,以结构在无损或健康状态下的Qr作为基准,将结构在未知状态下的Q与之进行对比,根据矩阵元素的变化来判断结构是否损伤。将矩阵转换为损伤特征向量V并欧拉范数归一化,其目的是消除荷载大小的影响。然后匹配两组向量,判断两者的一致性,公式如(11)所示,
(11)
式中CVAC是向量置信度准则,nc是向量V元素的数量,Vs为该向量的第s个元素。
,结构未知状态下Vs与无损状态下
比较,CVAC越接近1,说明两个向量的一致性越高。较低的CVAC值说明未知结构状态下V较基准向量
存在较大的差异,表明结构可能出现了损伤。
3. 数值模拟
试验梁是薄壁空心简支钢梁,截面的宽和高都是30 mm,壁厚1 mm,两支座中心之间的距离为3 m,如图1所示。钢材弹性模量206 GPa,密度7850 kg/m3。建立简支钢梁的有限元数值模拟,将该梁均分为10个梁单元,单元长30 cm,共11个节点,每个节点有竖向、转动2个自由度,梁共22个自由度。9个应变测点“均布”于梁顶面纵向中轴线上,测点间距、测点与支座中心距离都为30 cm (图1)。
对梁单元节点4施加一个竖直向下的三角激励模拟简支梁受到的冲击荷载作用。无损简支梁受三次激励作用,峰值分别为50N、100N和150N,激励时长都是0.03 s,“测得”简支梁在给定三角激励下9个测点的应变响应,采样频率为1000 Hz,共5 s的数据。在应变响应中添加白噪声模拟测试噪声,信噪比为80 dB。测点l1作为参考点,由9个测点的应变数据计算Rpl,再求得应变二次协方差矩阵Q。矩阵共9 × 9个元素,考虑该矩阵是对称矩阵,可利用其下(或上)三角元素或者对角元素构成损伤特征向量V识别结构的异常或损伤。下三角元素共45个。
3次激励工况下V向量两两匹配的CVAC值都接近1,结果表明在不同激励下V向量各元素间的比例一致,无损梁在不同锤击力作用下经归一化的V向量未发生改变,可以将该向量作为基准向量
,判断未知状态下的结构是否异常或损伤。
数值模型中结构损伤的模拟通过折减结构单元的刚度来实现,单元损伤系数
,(m = 1, 2, ∙∙∙, ne),ne是结构单元数,表明结构损伤的位置。当单元损伤系数αm等于1,表明结构没有损伤。设计以下损伤工况,单元4和单元8的刚度逐渐减小,
1)
;2)
,
;3)
,
;4)
,
。
3.1. 结构损伤程度对QCoS的影响
结构的频率和振型会随结构损伤的出现而改变,由综合式(2)、式(9)和式(10)可知,应变二次协方差矩阵元素Qrc包含1~N阶的结构频率和振型等信息。理论上,Qrc应该也会因结构的损伤而变化。图2横坐标中括号外数值表示梁单元4刚度折减值,括号内数值表示梁单元8刚度折减值。图中点划线呈现上扬趋势,实线表现为下降趋势。上扬说明QCoS随单元刚度的减小而渐增。Q33、Q43、Q44和Q73、Q74增幅最大,Q77、Q87、Q88、Q83、Q84增幅次之,Q53、Q63、Q31、Q41增幅小。其中二次协方差矩阵对角元素Q33、Q44、Q77、Q88较结构在无损状态时都有增大。结果显示,当测点lr和lc都是损伤单元的测点(l3、l4、l7、l8)时,Qrc随单元刚度的减小而增大。若仅有一个测点(lr或lc)是损伤单元的测点,随单元刚度的减小Qrc可能增大也可能减小,如Q31稍有增大、而Q93小幅减小。因此,当lr、lc中仅一点是损伤单元测点时,不能通过Q元素值的增大断定与测点相关单元的刚度会减小。若测点lr和lc都不是损伤单元的测点,Qrc随单元刚度的折减而减小。
以上分析结果证明了结构单元刚度的折减会导致Qrc的改变。此外,当Qrc是由损伤单元的测点响应计算得到,Qrc较结构未损伤时有明显增大,这一结果应该是与Qrc包含的振型信息有关。所以,可以考虑利用Qrc在结构损伤前后的改变定位结构的损伤。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 2. Curve of Qrc versus the damage extent
图2. Qrc与损伤程度的关系曲线
3.2. 损伤识别
基于单元刚度折减对Q矩阵元素的影响分析结果,选择主对角元素构成对损伤敏感的特征向量V。损伤识别步骤为:
1) 用式(9)和式(7)计算结构无损状态下的Q矩阵,取矩阵对角元素归一化构成基准向量Vr。
2) 重复步骤(1)计算得到结构未知状态下的V向量。
3) 用式(11)计算结构未知状态的V向量与Vr向量的向量置信度准则CVAC。计算V与Vr的向量元素差值δVs。综合CVAC值与特征向量元素差值δVs判断损伤和确定损伤位置。
验证基于应变二次协方差的梁损伤识别方法的准确性,首先通过CVAC值对结构的状态(无损或有损)进行初判。数值算例中各损伤工况下的CVAC值列于表1。当梁单元4和单元8引入5%的刚度折减,CVAC值减小2.8%,说明CVAC能反映小损伤引起的特征向量V的改变,梁结构的小损伤得到有效识别。当梁单元4刚度折减30%和单元8刚度折减20%时,CVAC值减小约12%,说明CVAC值随单元刚度的减小而减小,能反映结构损伤程度的变化。
对梁结构的状态进行初判后,再通过损伤特征向量元素差值δVs定位结构损伤。图3所示,δV3、δV4和δV7、δV8为正值,即Q33、Q44、Q77、Q88增大,说明测点3与测点4之间的单元4和测点7与测点8之间的单元8存在刚度减小的情况,且δV3、δV4和δV7、δV8随着单元4和单元8刚度的递减而递增。结果表明,通过损伤特征向量V的元素差值δVs能准确定位简支钢梁有限元模型中损伤单元4和单元8对应的两处损伤梁段。
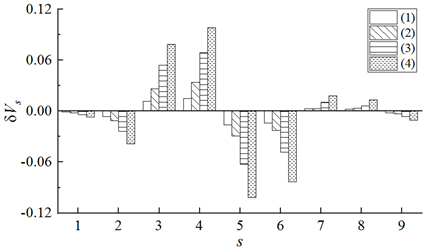
Figure 3. Difference between Vs values of the damaged and undamaged scenarios
图3. 有损与无损工况的Vs差值
4. 结论
本文提出利用结构的应变数据,在时域构造应变响应二次协方差矩阵对结构进行损伤识别。通过对矩阵元素与结构模态参数关系的推导,证明矩阵元素包含了结构固有的模态信息(频率、振型和阻尼)。结构的损伤会导致矩阵元素的改变,可以利用矩阵元素作为特征参数进行损伤识别。
通过对简支钢梁的数值模拟分析发现,若构成矩阵元素的测点响应都是损伤单元的测点数据,单元刚度的减小对该矩阵元素值的影响显著,且随着损伤程度的增加而增大。基于这一结论,可以选用应变二次协方差矩阵的对角元素构成损伤特征向量进行结构损伤识别。
通过梁结构损伤工况验证了该损伤识别方法的准确性。首先,通过向量置信度准则CVAC反映损伤特征向量在结构损伤前后发生的变化,当CVAC小于1时,可初步判断结构异常或存在损伤。再通过损伤特征向量的差值可准确定位梁结构的损伤位置。
基金项目
湖南省教育厅科学研究项目(19B106);湖南省自然科学基金(2021JJ50145);湖南省大学生创新训练项目(S202111527030)。