正弦函数状双层膜的自洽场模拟

Self-Consistent Field Simulation of Sinusoidal Function-Like Bilayers

摘要: 由脂质、表面活性剂和嵌段共聚物等两亲性分子自组装形成的双层膜在生物和物理化学体系中普遍存在。已有研究中模拟了圆柱状、球状双层膜，本文基于高分子自洽场理论，引入界面约束来考察正弦柱面状双层膜，模拟其结构，并计算其自由能。结果发现当随着正弦状双层膜的振幅变大时，自洽场模拟得到的双层膜的形状已不再是标准的正弦函数状。

Abstract: Bilayers formed by the self-assembly of amphiphilic molecules such as lipids, surfactants and block copolymers are commonly found in biological and physicochemical systems. Cylindrical and spherical bilayers have been simulated in previous studies. Based on the self-consistent field theory of polymers, this paper introduces interface constraints to investigate the sinusoidal cylindrical bilayer membranes, simulate their structures, and calculate their free energies. It is found that when the amplitude of the sinusoidal bilayer becomes larger, the shape of the bilayer obtained from the self-consistent field simulation is no longer the standard sine function shape.

1. 引言

高分子化合物是通过共价键重复连接得到的分子量可达10⁴以上的大分子，由于高分子的分子量较大，高分子链变得很复杂，从而使得高分子材料有许多优良的性能，因此被广泛应用于社会生产的各个领域和日常生活的各个角落。高分子自组装成双层膜是形成蛋白质、细胞乃至生命的一个重要途径，而嵌段共聚物等两亲性聚合物的自组装具有许多新奇的潜在应用价值 [1] [2] ，而开发由两亲性嵌段共聚物自组装的聚合物混合材料，例如超越脂质膜，在生物医学和生物技术中有很大的应用前景，如模拟细胞表面和产生生物相容性和生物活性药物递送系统。因此，嵌段共聚物的自组装为生物膜的研究提供了一种模仿手段。

双层膜是由两亲分子自组装形成，因此双层膜的性质在很大程度上由两亲分子的性质决定。在介观尺度下，可用二维曲面唯象地刻画双层膜，当曲面的曲率较小时，其形变能可用Helfrich线性弹性理论来刻画 [3] [4] 。在过去的几十年里，为了测量膜的弹性参数，人们发展出了许多技术手段 [5] [6] 、模拟方法 [7] [8] [9] 以及理论方法 [10] [11] 来获取双层膜的弹性参数。一个有效的策略是将膜弯曲成不同几何形状(如平面、圆柱体和球体)的双层膜，计算出不同曲率时膜的能量，与Helfrich能量泛函作对比来得到其中的系数。这个策略在理论研究中比较容易实现。已有研究中模拟了柱状、球状这些特殊形状的双层膜，并计算了不同曲率的无限平面、圆柱状和球状双层膜的净自由能 [12] [13] [14] 。然而本文讨论的是一般形状的双层膜，在自洽场理论的框架下进行模拟，通过引入界面约束来获得正弦状的双层膜，模拟其结构，并计算其自由能。

2. 自洽场模型

2.1. 柔柔A/AB自洽场模型

本研究中使用的分子模型是AB两嵌段共聚物和A均聚物的二元混合物模型。这是一个通用的模型，其中，用AB两嵌段共聚物来模拟两亲性分子，而用A均聚物来模拟两亲性溶剂分子。此外，由于考虑的是柔性分子，于是采用高斯链模型。

在正则系综下，考虑包含 $n_h$ 条A均聚物和 $n_c$ 条AB两嵌段共聚物的混合物，每条AB分子由 $N_A$ 个A单体和 $N_B$ 个B单体汇聚而成，且聚合度为 $N=N_A+N_B$ ，而每条A分子由 $N_h$ 个A单体构成。现我们假设A/AB混合物体系是不可压缩的，并且两个单体(A和B)具有相同的单体密度 ${\rho }_{\text{0}}$ (或每个单体占用相同的体积 $1/{\rho }_{\text{0}}$ )。共聚物中A嵌段、B嵌段及A均聚物的体积分数分别用 $f_A$ 、 $f_B=1-f_A$ 及 $f_h=N_h/N$ 来表示，A嵌段和B嵌段的回旋半径用 $R_g^A=\sqrt{f_{A}N{l}_a^2/6}$ 和 $R_g^A=\sqrt{f_{B}N{l}_b^2/6}$ 来表示，其中 $l_a$ 和 $l_b$ 分别为A单体和B单体的统计链段长。我们将 $R_g:=\sqrt{N{l}_a^2/6}$ 设为无量纲化中的单位空间长度，并定义 $a=l_a/l_a=1$ ，定义 $b=l_b/l_a$ 为A嵌段与B嵌段之间的几何非对称性参数。A单体和B单体之间的相互作用的强弱用Flory-Huggins参数 $\chi N$ 来描述。最后，利用共聚物的化学势 ${\mu }_c$ 或相应的化学势的活性度 $z_c=\exp \left({\mu }_c\right)$ 来控制共混物中两嵌段共聚物的平均浓度。

在自洽场理论(SCFT)的框架下，巨正则系综中A/AB混合物体系的自由能(有效哈密顿量)为

$\begin{array}{c}\frac{NF}{k_{B}T{\rho }_0}={\displaystyle \int \text{d}r[\chi N{\varphi }_A\left(r\right){\varphi }_B\left(r\right)-{\omega }_A\left(r\right){\varphi }_A\left(r\right)-{\omega }_B\left(r\right){\varphi }_B\left(r\right)}-\xi \left(r\right)\left({\varphi }_A\left(r\right)+{\varphi }_B\left(r\right)-1\right)\\ +\psi G_{\epsilon }\left(r-r_1\right)\left({\varphi }_A\left(r\right)-{\varphi }_B\left(r\right)\right)]-z_c{Q}_c-Q_h.\end{array}$ (1)

其中， ${\varphi }_{\alpha }\left(r\right)$ 和 ${\omega }_{\alpha }\left(r\right)$ 分别为单体 $\alpha$ 的局部浓度以及对应的场( $\alpha =A,B$ )， $\xi \left(r\right)$ 为保持系统不可压的Lagrange乘子场；另一个Lagrange乘子场 $\psi$ 的引入是为了稳定不同几何形状的双层膜；高斯函数 $G_{\epsilon }\left(r-r_1\right)$ 用于确保场 $\psi$ 只作用在双层膜外侧界面 $r=r_1$ 处； $G_{\epsilon }\left(r-r_1\right)\left({\varphi }_A\left(r\right)-{\varphi }_B\left(r\right)\right)$ 为约束项。此外，式子中的最后两项 $Q_c$ 和 $Q_h$ 分别为AB分子和A分子的单链配分函数。

在SCFT中，计算的基本量是聚合物的概率分布函数(或传播子)。具体地， $q_A^h\left(r,s\right)$ 为A均聚物的传播子， $q_A^{\pm }\left(r,s\right)$ ， $q_B^{\pm }\left(r,s\right)$ 为AB两嵌段共聚物的传播子。这些传播子通过求解平均场( ${\omega }_A\left(r\right)$ 和 ${\omega }_B\left(r\right)$ )中柔性聚合物链的修正扩散方程(MDEs)得到

$\begin{array}{l}\frac{\partial }{\partial s}{q}_A^h\left(r,s\right)=\left(a^2{\nabla }_r^2-{\omega }_A\left(r\right)\right)q_A^h\left(r,s\right),s\in \left(0,f_h\right)\\ \frac{\partial }{\partial s}{q}_A^{\pm }\left(r,s\right)=\left(a^2{\nabla }_r^2-{\omega }_A\left(r\right)\right)q_A^{\pm }\left(r,s\right),s\in \left(0,f_A\right)\\ \frac{\partial }{\partial s}{q}_B^{\pm }\left(r,s\right)=\left(b^2{\nabla }_r^2-{\omega }_B\left(r\right)\right)q_B^{\pm }\left(r,s\right),s\in \left(0,f_B\right)\end{array}$ (2)

带有初值条件，

$\begin{array}{l}{q}_A^h\left(r,0\right)=q_A^{-}\left(r,0\right)=q_B^{-}\left(r,0\right)=1,\\ q_A^{+}\left(r,0\right)=q_B^{-}\left(r,f_B\right),\\ q_B^{+}\left(r,0\right)=q_A^{-}\left(r,f_A\right).\end{array}$ (3)

单链配分函数 $Q_c$ 和 $Q_h$ 可通过传播子求得，

$Q_c={\displaystyle \int \text{d}r{q}_A^{+}\left(r,f_A\right),}$ (4)

$Q_h={\displaystyle \int \text{d}r{q}_A^h\left(r,f_h\right).}$ (5)

同样地，A单体和B单体的局部浓度 ${\varphi }_A\left(r\right)$ 、 ${\varphi }_B\left(r\right)$ 也可通过传播子得到，

${\varphi }_A\left(r\right)={\varphi }_A^h+{\varphi }_A^c={\displaystyle {\int }_0^{f_h}\text{d}s{q}_A^h}\left(r,s\right)q_A^h\left(r,f_h-s\right)+z_c{\displaystyle {\int }_0^{f_A}\text{d}s{q}_A^{-}}\left(r,s\right)q_A^{+}\left(r,f_A-s\right),$ (6)

${\varphi }_B\left(r\right)=z_c{\displaystyle {\int }_0^{f_B}\text{d}s{q}_B^{-}}\left(r,s\right)q_B^{+}\left(r,f_B-s\right).$ (7)

进一步有A/AB混合物体系的自洽场方程为：

${\omega }_A\left(r\right)=\chi N{\varphi }_B\left(r\right)-\xi \left(r\right)+\psi G_{\epsilon }\left(r-r_1\right),$ (8)

${\omega }_B\left(r\right)=\chi N{\varphi }_A\left(r\right)-\xi \left(r\right)-\psi G_{\epsilon }\left(r-r_1\right),$ (9)

${\varphi }_A\left(r\right)+{\varphi }_B\left(r\right)=1,$ (10)

${\displaystyle \int \text{d}r}{G}_{\epsilon }\left(r-r_1\right)\left({\varphi }_A\left(r\right)-{\varphi }_B\left(r\right)\right)=0.$ (11)

2.2. 几何约束

在能量泛函中添加约束项 $H_G$ ，使得在双层膜的外侧界面 $\Gamma \left(r_1\in \Gamma \right)$ 处满足

${\displaystyle \int \text{d}r{G}_{\epsilon }}\left(r-r_1\right)\left[{\varphi }_A\left(r\right)-{\varphi }_B\left(r\right)\right]=0.$ (12)

$H_G$ 的形式为：

$H_G=\frac{1}{V}{\displaystyle \int \text{d}r\psi G_{\epsilon }}\left(r-r_1\right)\left[{\varphi }_A\left(r\right)-{\varphi }_B\left(r\right)\right].$ (13)

其中 $G_{\epsilon }$ 为高斯函数， $\psi$ 是拉格朗日乘子。具体地，高斯函数为

$G_{\epsilon }\left(r\right)=C_{\epsilon }\exp \left(-\frac{{\left|r\right|}^2}{2{\epsilon }^2}\right).$ (14)

其中 $G_{\epsilon }$ 为常数。

通过引入平行曲面来构造若干约束点。具体的做法是，逐点沿着正弦状双层膜 $y=f\left(x\right)$ 的外法向 $n$ 向外延伸一定的距离，从而得到此平行曲面，其中外法向

$n=\frac{\text{1}}{\sqrt{\text{1}+f^{\prime }{\left(x\right)}^2}}\left(-f^{\prime }{\left(x\right)}^2,1\right).$ (15)

3. 数值方法

对于自洽场方程组的求解，重点在于求解传播子方程。假设x方向和y方向均为周期边界条件，于是使用拟谱方法进行求解。考虑

$\frac{\partial }{\partial s}q\left(r,s\right)=a^2{\nabla }_r^{2}q\left(r,s\right),$ (16)

$q\left(r,0\right)=q_0\left(r\right).$ (17)

如果平方可积函数 $f\left(r\right)\left(r\in R^2\right)$ 具有周期性

$f\left(r+At\right)=f\left(r\right).$ (18)

其中 $A=\left(a_1,a_2\right),a_i,t\in Z^2$ 。将 $f\left(r\right)$ 进行傅里叶展开有

$f\left(r\right)={\displaystyle \underset{k\in Z^2}{\sum }\hat{f}\left(Bk\right){\text{e}}^{iBk\cdot r}}.$ (19)

其中 $B=\left(b_1,b_2\right),b_j,k\in Z^2$ 。此外， $B^{\text{T}}A=2\pi I$ ， $a_i\cdot b_j=2\pi {\delta }_{ij}$ ，I为单位矩阵。然后我们通过以下公式获得傅里叶系数

$\hat{f}\left(Bk\right)=\frac{1}{\left|V_A\right|}{\displaystyle {\int }_{V_A}f\left(r\right){\text{e}}^{-iBk\cdot r}\text{d}r}.$ (20)

其中 $V_A$ 为平行四边形的面积。接下来，对方程(16)(17)做傅里叶变换得到

$\begin{array}{l}\frac{\partial }{\partial s}\hat{q}\left(Bk,s\right)=-a^2{\left|Bk\right|}^2\hat{q}\left(Bk,s\right),\\ \hat{q}\left(Bk,0\right)={\hat{q}}_0\left(Bk\right).\end{array}$ (21)

于是，具体的计算步骤可总结为：

· 由初值 $q_0\left(r\right)$ 得到 ${\hat{q}}_0\left(Bk\right)$ ，

· 求解式(21)得 $\hat{q}\left(Bk,s\right)={\hat{q}}_0\left(Bk\right){\text{e}}^{-a^2{\left|Bk\right|}^{2}s}$ ，

· 将 $\hat{q}\left(Bk,s\right)$ 代入Fourier级数中得 $q\left(r,s\right)={\displaystyle \underset{k\in Z^2}{\sum }\hat{q}\left(Bk,s\right){\text{e}}^{iBk\cdot r}}$ 。

4. 数值结果

选择典型的模型参数 $\chi N=20$ ， $f_A=0.5$ ， $f_B=0.5$ ， $\beta =\text{1}$ 。空间的离散点数为 $N_x=100$ ， $N_y=200$ ，链长的离散点数为 $N_s=300$ ，以保证自由能的计算误差小于10⁻¹²。在场的迭代中，终止条件取为自洽场方程组的 $L^{\text{2}}$ 范数误差Err小于10⁻⁷，这里 $Er{r}^2$ 定义为

$Er{r}^2={\Vert \frac{\delta H}{{\omega }_A}\Vert }^2+{\Vert \frac{\delta H}{{\omega }_B}\Vert }^2.$ (22)

其中H为式(1)。

图1中展示的是通过自洽场模拟得到的周期为 $T=11$ 的正弦状双层膜的相图，分别为当 $a=1$ ， $a=\text{4}$ ， $a=\text{8}$ ， $a=1\text{2}$ 时的相图。从图1中我们可以观察得到，当振幅a变大后，双层膜的相图已不再是标准的正弦函数状，也就意味着约束点并不能完全固定双层膜的形状，从而需通过序参量来确定双层膜的形状。 接着，图2为能量曲线图，即正弦状双层膜的净能量 $F_{ex}$ 随振幅a变化的曲线图。

$(a=1)$ $(a=\text{4})$ $(a=\text{8})$ $(a=\text{12})$

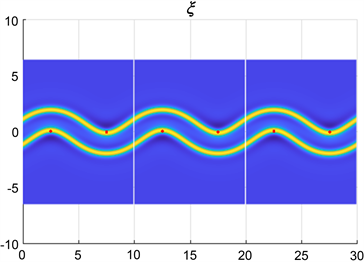
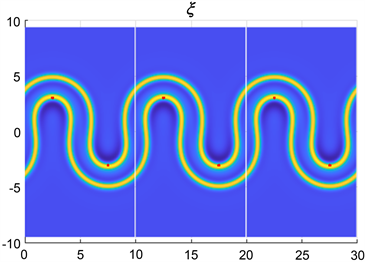
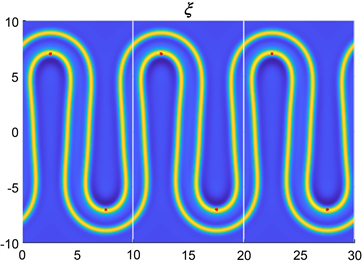
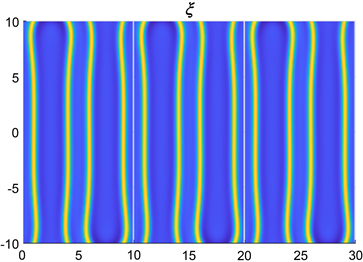
Figure 1. Phase diagrams of sinusoidal bilayers under constraint

图1. 约束下的正弦状双层膜的相图

Figure 2. Energy curve

图2. 能量曲线

5. 结论和展望

本文基于高分子自洽场理论，通过引入界面约束来获得正弦状双层膜，模拟其结构，并计算其自由能，结果发现当随着正弦状双层膜的振幅变大时，自洽场模拟得到的双层膜的形状已不再是标准的正弦函数状，也就意味着约束点并不能完全固定双层膜的形状，从而需通过序参量来确定双层膜的形状。下一步将继续通过自洽场模拟正弦柱面形状的双层膜，计算其自由能，与Helfrich模型的预测结果进行比较，以检验Helfrich模型的精度。