相对论物质波的生物钟和人类平均年龄84岁的计算

Biological Clock of Relativistic Matter Wave and Calculation of Human Mean Lifespan 84 Years

摘要: 研究发现，相对论物质波为人类提供了一个生物钟。本文首先给出了两个例子来展示相对论物质波的有效性。其次，对太阳黑子周期、地球大气环流和人类生物钟进行了研究，推导出了钟公式。结果表明，太阳黑子周期为10.93年，人类平均年龄为84岁。为生物钟设计了抗衰老指南。

Abstract: It is found that relativistic matter wave provides a biological clock for human beings. At the first, two examples are given to show the validity of the relativistic matter wave. Next, the sunspot period, earth’s atmosphere circulation and human biological clock are investigated, the clock formula is de-rived. As the results, the period of sunspot cycle is calculated to be 10.93 years, the human mean lifespan is calculated to be 84 years. A guidance of anti-ageing is devised for the biological clock.

1. 引言

今年是德布罗意物质波倡议100周年。1923年，路易斯·德布罗意(Louis de Broglie)将黑体辐射视为光量子气体 [1] ，他试图将光量子的概念与干涉和衍射现象相协调。1923年和1924年，路易斯·德布罗意提出了物质表现为波的概念 [2] 。今天它被称为德布罗意物质波。

长期以来，人们一直试图将德布罗意物质波推广到行星波，但是遇到许多困难；传统的量子理论不能正确处理一些引力问题 [3] [4] [5] 。近年来，推广的相对论物质波被提出并应用于太阳系来解释量子引力效应，这一方法为量子引力研究提供了一种新的方法。考虑一个粒子，它的相对论物质波由下式给出

$\psi =\exp \left(\frac{i\beta }{c^3}{\displaystyle {\int }_0^x\left(u_1\text{d}{x}_1+u_2\text{d}{x}_2+u_3\text{d}{x}_3+u_4\text{d}{x}_4\right)}\right)$ (1)

这里u是粒子的四维速度，β是由实验确定的极值加速度 [6] 。本文首先给出了两个例子来展示相对论物质波的有效性；其次，对太阳黑子周期、地球大气环流和人类生物钟进行了研究，推导出了钟公式。结果表明，太阳黑子周期为10.93年，人类平均年龄为84年。

2. 验证的例子1：确定太阳物质密度和半径

Figure 1. (a) The head of the relativistic matter wave may overlap with its tail; (b) The inner planets are quantized

图1. (a)一颗行星绕太阳运行；(b)对内部的一些轨道半径进行了量化

玻尔轨道模如图1(a)所示，量子化规则：行星的圆形轨道周长是相对论物质波波长的整数n倍，由(1)式得到

$\begin{array}{l}\frac{\beta }{c^3}{\displaystyle {\oint }_L{v}_l\text{d}l}=2\pi n\\ v_l=\sqrt{\frac{GM}{r}}\end{array}\}\Rightarrow \sqrt{r}=\frac{c^3}{\beta \sqrt{GM}}n;n=0,1,2,\cdots$ (2)

这种轨道量子化规则在太阳系中只取得了一半的成功，如图1(b)所示，其中太阳、水星、金星、地球和火星满足这个量子化方程；而其它的外行星则失效。但是，因为我们只研究太阳、水星、金星、地球和火星之间的量子引力效应，所以这个轨道量子化规则作为基础量子理论已经足够好了。在图1(b)中，蓝色直线表示量化轨道之间的线性回归关系，因此拟合计算给出 $\beta =2.961520\text{e}+10\left(\text{m}/{\text{s}}^{\text{2}}\right)$ 。量子数 $n=\text{3},\text{4},\text{5},\cdots$ 被分配给太阳系各个行星，太阳也被分配了一个量子数n = 0，因为太阳处于中心状态。

相对论物质波可以用来确定太阳的物质密度和半径。

在中心状态n = 0且具有一定大小的情况下，如果相对论物质波的相干长度足够长，当粒子在时空中的闭合轨道中移动时，其头部可能与尾部重叠，如图1(a)所示。重叠波由下式给出

$\begin{array}{l}\psi =\psi \left(r\right)T\left(t\right)\\ \psi \left(r\right)=1+{\text{e}}^{i\delta }+{\text{e}}^{i2\delta }+\cdots +{\text{e}}^{i\left(N-1\right)\delta }=\frac{1-\exp \left(iN\delta \right)}{1-\exp \left(i\delta \right)}\\ \delta \left(r\right)=\frac{\beta }{c^3}{\displaystyle {\oint }_L\left(v_l\right)\text{d}l}=\frac{2\pi \beta \omega r^2}{c^3}\end{array}$ (3)

式中N是重叠数，该重叠数由相对论物质波的相干长度来确定，δ是一次轨道运动后的相位差变化，w是太阳自转的角速度。在光学中，上述方程是多缝干涉公式，对于较大的N，称为Fabry-Perot干涉公式。

在量子力学中根据Max Born的解释， ${\left|\psi \right|}^2$ 等于找到电子的概率；在天体物理学方面， ${\left|\psi \right|}^2$ 等于在天文尺度上平均找到一个核子(质子或中子)的概率，不管它是处在束缚态还是处在等离子体态，因为所有质量主要由核子质量构成，所以

${\left|\psi \right|}^2\propto \text{nucleon-density}\propto \rho$ (4)

根据光学的多缝干涉公式，重叠数N为

$N^2=\frac{{\left|\psi {\left(0\right)}_{multi-wavelet}\right|}^2}{{\left|\psi {\left(0\right)}_{one-wavelet}\right|}^2}=\frac{{\rho }_{core}}{{\rho }_{surface\text{\_}gas}}$ (5)

太阳核心的物质密度为1408 (kg/m³)，太阳表面由对流区组成，平均物质密度为2e − 3 (kg/m³) [7] 。本文中，太阳半径定义在物质密度等于4e − 3 (kg/m³)的地方，太阳的相对论物质波的重叠数N计算为N = 593。

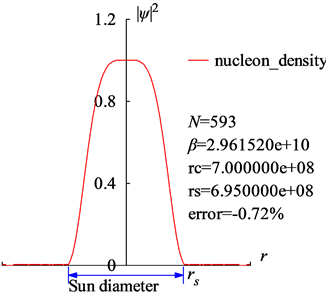
Figure 2. The nucleon distribution ${\left|\psi \right|}^2$ in the Sun is calculated in the radius direction

图2. 计算了半径方向上的太阳的物质分布 ${\left|\psi \right|}^2$

< Clet2020 Script > //C source code [9]

int i,j,k,m,n,N,nP[10];

double beta,H,B,M,r,r_unit,x,y,z,delta,D[1000],S[1000], a,b,rs,rc,omega,atm_height; char str[100];

main(){k=150;rs=6.95e8;rc=0;x=25.05;omega=2*PI/(x*24*3600);n=0; a=1408/0.004; N=sqrt(a);

beta=2.961520e10;H=SPEEDC*SPEEDC*SPEEDC/beta;M=1.9891E30; atm_height=2e6; r_unit=1E7;

for(i=-k;i

if(r

x=1;y=0; for(j=1;j

S[n]=i;S[n+1]=z; if(i>0 &&rc==0 && z<0.0001) rc=r; n+=2;}

SetAxis(X_AXIS,-k,0,k#ifr; ; ; ;);SetAxis(Y_AXIS,0,0,1.2#if|ψ|#su2#t;0;0.4;0.8;1.2;);

DrawFrame(FRAME_SCALE,1,0xafffaf); z=100*(rs-rc)/rs;

SetPen(1,0xff0000);Polyline(k+k,S,k/2,1 nucleon_density); SetPen(1,0x0000ff);

r=rs/r_unit;y=-0.05;D[0]=-r;D[1]=y;D[2]=r;D[3]=y; Draw(ARROW,3,2,XY,10,100,10,10,D);

Format(str#ifN#t=%d#n#ifβ#t=%e#nrc=%e#nrs=%e#nerror=%.2f%,N,beta,rc,rs,z);

TextHang(k/2,0.7,0,str);TextHang(r+5,y/2,0#ifr#sds#t);TextHang(-r,y+y,0Sun diameter);

}#v07=?>A

太阳赤道的自转角速度是 $\omega =\text{2}\pi /\left(25.05\times 24\times 3600\right)$ ，单位s⁻¹。其质量1.9891e + 30 (kg)，已知的半径6.95e + 8 (m)，平均密度1408 (kg/m³)，极值加速度 $\beta =2.961520\text{e}10\left(\text{m}/{\text{s}}^{\text{2}}\right)$ 。根据N = 593，计算出来的太阳的物质分布 ${\left|\psi \right|}^2$ 在图2中，它与太阳内部的一般描述吻合 [8] 。在图2中，太阳半径计算值为r = 7e + 8 (m)，相对误差为0.72%，这表明太阳半径与太阳自转有强烈的依赖关系。

3. 验证的例子2：确定地球物质密度和半径

月球被分配了一个n = 2的量子数，因为一些准卫星的近地点几乎到达了轨道n = 1的深度，如图3所示。这里，常数 $\beta =1.377075\text{e}+\text{14}\left(\text{m}/{\text{s}}^{\text{2}}\right)$ 由地球和月球之间的直线通过方程式(2)唯一的确定。

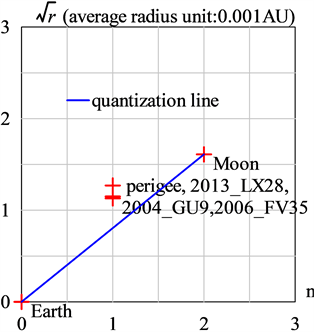
Figure 3. Quantized orbits for the moon and Earth’s quasi satellites

图3. 月亮和地球准卫星的量子化轨道

地球的自转角速度是 $\omega =\text{2}\pi /\left(24\times 3600\right)$ ，单位s⁻¹。其质量为5.97237e24 (kg)，已知的半径为6.378e + 6 (m)，平均密度为5530 (kg/m³)，极值加速度为 $\beta =1.377075\text{e14}\left(\text{m}/{\text{s}}^{\text{2}}\right)$ 。地球表面覆盖着空气和水蒸气，地球半径定义在海平面，其物质密度等于1.29 (kg/m³)。根据(5)式计算，地球的相对论物质波的重叠数为N = 65。计算出来的半径方向上的物质分布 ${\left|\psi \right|}^2$ 如图4(a)所示。计算出地球半径r = 6.4328e + 6 (m)，相对误差为0.86%。计算出了海拔2000公里高度内大气中的干涉次峰，如图4(b)所示，这与空间碎片观测结果吻合很好 [10] [11] [12] 。

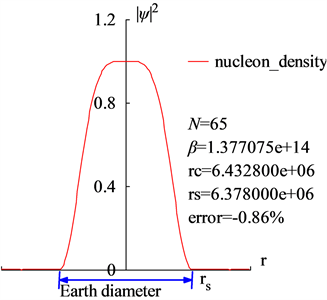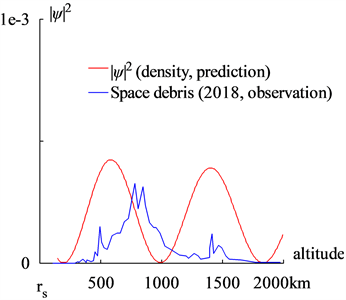(a) (b)

Figure 4. (a) The radius of the Earth is calculated out r = 6.4328e + 6 (m) with a relative error of 0.86% by the interference of its relativistic matter wave; (b) The prediction of the space debris distribution up to 2000 km altitude

图4. (a)通过其相对论物质波的干涉计算出地球半径r = 6.4328e + 6 (m)，相对误差为0.86%；(b) 2000公里高空内空间碎片分布预测

< Clet2020 Script > //C source code [9]

int i,j,k,m,n,N,nP[10]; double H,B,M,v_r,r,AU,r_unit,x,y,z,delta,D[10],S[1000];

double rs,rc,rot,a,b,atm_height,beta; char str[100];

main(){k=80;rs=6.378e6;rc=0;atm_ height=1.5e5;n=0; N=65;

beta=1.377075e+14;H=SPEEDC*SPEEDC*SPEEDC/beta;

M=5.97237e24;AU=1.496E11;r_unit=1e-6*AU; rot=2*PI/(24*60*60);//angular speed of the Earth

for(i=-k;i

if(r

delta=2*PI* v_r/H; y=SumJob(SLIT_ADD,@N,@delta,D); y=y/(N*N);

if(y>1) y=1; S[n]=i;S[n+1]=y; if(i>0 &&rc==0 && y<0.001) rc=r;n+=2;}

SetAxis(X_AXIS,-k,0,kr; ; ; ;);SetAxis(Y_AXIS,0,0,1.2#if|ψ|#su2#t;0;0.4;0.8;1.2;);

DrawFrame(FRAME_SCALE,1,0xafffaf); x=50;z=100*(rs-rc)/rs;

SetPen(1,0xff0000);Polyline(k+k,S,k/2,1 nucleon_density);

r=rs/r_unit;y=-0.05;D[0]=-r;D[1]=y;D[2]=r;D[3]=y;

SetPen(2,0x0000ff); Draw(ARROW,3,2,XY,10,100,10,10,D);

Format(str#ifN#t=%d#n#ifβ#t=%e#nrc=%e#nrs=%e#nerror=%.2f%,N,beta,rc,rs,z);

TextHang(k/2,0.7,0,str);TextHang(r+5,y/2,0r#sds#t);TextHang(-r,y+y,0Earth diameter);

}#v07=?>A#t

< Clet2020 Script > //C source code [9]

int i,j,k,m,n,N,nP[10]; double H,B,M,v_r,r,AU,r_unit,x,y,z,delta,D[10],S[10000];

double rs,rc,rot,a,b,atm_height,p,T,R1,R2,R3; char str[100];int Debris[96]={110,0,237,0,287,0,317,2,320,1,357,5,380,1,387,4,420,2,440,3,454,14,474,9,497,45,507,26,527,19,557,17,597,34,634,37,664,37,697,51,727,55,781,98,808,67,851,94,871,71,901,50,938,44,958,44,991,37,1028,21,1078,17,1148,10,1202,9,1225,6,1268,12,1302,9,1325,5,1395,7,1395,18,1415,36,1429,12,1469,22,1499,19,1529,9,1559,5,1656,4,1779,1,1976,1,};

main(){k=80;rs=6.378e6;rc=0;atm_ height=1.5e5;n=0; N=65;

H=1.956611e11;M=5.97237e24;AU=1.496E11;r_unit=1e4;

rot=2*PI/(24*60*60);//angular speed of the Earth

b=PI/(2*PI*rot*rs*rs/H); R1=rs/r_unit;R2=(rs+atm_height)/r_unit;R3=(rs+2e6)/r_unit;

for(i=R2;i

y=SumJob(SLIT_ADD,@N,@delta,D); y=1e3*y/(N*N);// visualization scale:1000

if(y>1) y=1; S[n]=i;S[n+1]=y;n+=2;}

SetAxis(X_AXIS,R1,R1,R3altitude; r#sds#t;500;1000;1500;2000km ;);

SetAxis(Y_AXIS,0,0,1#if|ψ|#su2#t;0; ;1e-3;);DrawFrame(FRAME_SCALE,1,0xafffaf); x=R1+(R3-R1)/5;

SetPen(1,0xff0000);Polyline(n/2,S,x,0.8#if|ψ|#su2#t (density, prediction));

for(i=0;i<48;i+=1) {S[i+i]=R1+(R3-R1)*Debris[i+i]/2000; S[i+i+1]=Debris[i+i+1]/300;}

SetPen(1,0x0000ff);Polyline(48,S,x,0.7Space debris (2018, observation) );}#v07=?>A#t

4. 太阳黑子的周期

在量子力学中，波的相干长度经常被提及，但很少讨论波的相干宽度，因为后者不会成为电子、核子或光子的关心问题，而它却成为天体物理学的关心问题。分析观测数据告诉我们，在行星尺度上，相对论物质波的相干宽度可以延伸到1000公里甚至更多，如示意图5(a)所示，重叠可以在宽度方向上发生，从而为波的干涉带来新的特性。

在太阳的对流区，相邻的对流阵列形成顶层气流、中层气体和底层气流，就像电磁学中的分子电流概念。顶层气流和中层气体之间存在明显的速度差，如图5(b)所示，其中它们的相对论物质波的干涉为

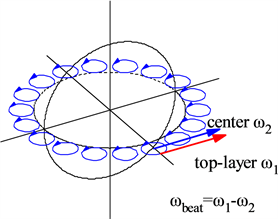(a) (b)

Figure 5. (a) Illustration of overlapping in the coherent width direction; (b) In convective rings at the equator, the speed difference causes a beat frequency

图5. (a)相干宽度方向上的重叠示意图；(b)赤道处的对流环，速度差导致拍

$\begin{array}{l}\psi ={\psi }_{top}+C{\psi }_{middle}\\ {\psi }_{top}=\exp \left[\frac{i\beta }{c^3}{\displaystyle {\int }_L\left(v_1\text{d}l+\frac{-c^2}{\sqrt{1-v_1^2/c^2}}\text{d}t\right)}\right]\\ {\psi }_{middle}=\exp \left[\frac{i\beta }{c^3}{\displaystyle {\int }_L\left(v_2\text{d}l+\frac{-c^2}{\sqrt{1-v_2^2/c^2}}\text{d}t\right)}\right]\end{array}$ (6)

这里C是耦合系数。它们的波动干涉会导致拍现象

$\begin{array}{l}{\left|\psi \right|}^2={\left|{\psi }_{top}+C{\psi }_{middle}\right|}^2=1+C^2+2C\cos \left[\frac{\text{2}\pi }{{\lambda }_{beat}}{\displaystyle {\int }_L\text{d}l-\frac{\text{2}\pi }{T_{beat}}t}\right]\\ \frac{\text{2}\pi }{T_{beat}}=\frac{\beta }{c^3}\left(\frac{c^2}{\sqrt{1-v_1^2/c^2}}-\frac{c^2}{\sqrt{1-v_2^2/c^2}}\right)\simeq \frac{\beta }{c^3}\left(\frac{v_1^2}{2}-\frac{v_2^2}{2}\right)\\ \frac{\text{2}\pi }{{\lambda }_{beat}}=\frac{\beta }{c^3}\left(v_1-v_2\right);V=\frac{{\lambda }_{beat}}{T_{beat}}=\frac{1}{2}\left(v_1+v_2\right)\end{array}$ (7)

它们的速度计算如下

$\begin{array}{l}{v}_1\approx 6100\left(\text{m}/\text{s}\right)\left(\approx \text{observedinEvershedflow}\right)\\ v_2=\omega r_{middle}=2017\left(\text{m}/\text{s}\right)\left(\text{solarrotation}\right);\end{array}$ (8)

这里将Evershed流视为顶层气流的喷发，其速度有报导为大约6000 m/s [13] ，另外，用热力学方法在绝对温度5700 K估算出v₁ = 6200 m/s [6] 。这里取v₁ = 6100 m/s，这样计算出的它们的节拍周期T_beat是一个非常特别的值：10.93 (年)，与太阳黑子周期值(平均11年)基本一致。

$T_{beat}\simeq \frac{4\pi c^3}{\beta \left(v_1^2-v_2^2\right)}=10.93\left(\text{years}\right)$ (9)

使用相对论物质波计算出的节拍周期，与11年平均值的相对误差为0.6%。这个节拍的解释为：它是一个核子密度的上下波动，驱动着太阳黑子周期地演化。拍波长 ${\lambda }_{beat}$ 太长，无法观察，只有节拍周期很容易被观察到，赤道圆周2pr只占拍波长的很小一部分，如图6所示。

$\frac{2\pi r}{{\lambda }_{beat}}=0.0031$ (10)

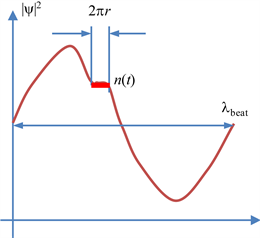
Figure 6. The equatorial circumference 2pr only occupies a little part of the beat wavelength, what we see is the expansion and contraction of the nucleon density

图6. 赤道圆周2pr只占拍波长的很小一部分，我们看到的是核子密度的膨胀和收缩

在上面的计算中，虽然这仅仅是一个近似模型，但太阳半径、太阳自转、太阳密度和太阳常数β之间存在明显的关联性。

5. 大气循环与季节钟

(a) (b)

Figure 7. (a) Mutual cascade-interference will lead to the symmetry of the earth’s density distribution; (b) Zonal winds on Jupiter (the photo from public News)

图7. (a)相互级联干涉将导致地球密度分布的球对称性；(b)木星上的带状风(照片来自公共新闻)

纬度角A的地壳的相对论物质波 ${\psi }_A$ ，在其相干宽度范围内，它将与相邻波相互干涉。由于地壳主要由致密物质组成，它们的相互级联干涉(cascade-interference)将导致相对论物质波具有球对称性，从而使纬度角A处的相对论物质波 ${\psi }_A$ 等于赤道处的相对论物质波 ${\psi }_{equator}$ ，如图7(a)所示。地球物质密度分布的球对称性支持了这一特性：

$\begin{array}{l}\text{sphericalsymmetry:}\rho \left(r,A,\phi \right)=\rho \left(r\right)\Rightarrow \psi \left(r,A,\phi \right)=\psi \left(r\right)\\ \text{or:}{\psi }_A={\psi }_{equator}=0.0031\end{array}$ (11)

相反，在稀薄的大气中，风和云在天空中自由地广泛分布，因为它们的相干宽度范围内的级联干涉(cascade-interference)可以忽略。

使用相干宽度概念，考虑纬度角A处的空气 ${\psi }_A$ 与同一纬度的地壳 ${\psi }_{shell}$ 之间的干涉，它们的干涉是

$\begin{array}{l}\psi \left(r,A\right)={\psi }_{air}\left(r,A\right)+C{\psi }_{shell}\left(r,A\right)={\psi }_{air}\left(r,A\right)+C{\psi }_{shell\text{\_}equator}\left(r\right)\\ T_{beat}\simeq \frac{4\pi c^3}{\beta \left(v_{shell\_equator}^2-v_{air}^2\right)}\\ v_{shell\_equator}=\omega r\\ v_{air}=\omega r\cos \left(A\right)+v_{wind}+v_{sun\text{\_}effect}\end{array}$ (12)

其中C表示耦合系数(与它们的距离和质量分数相关)，它们的干涉导致一个节拍现象。风的正方向定义为从西向东的方向，其中v_{sun_effect}代表了太阳对空气的作用。这个拍现象表现如下。

(1) 受迫震荡

由于地球自转轴相对于地球轨道平面的倾斜23.5˚，太阳直接照耀的纬度一年四季在A = 23.5˚S~23.5˚N之间变化。例如，每年春季直接照耀的纬度在北半球A₁ = 12˚N附近。空气受到太阳辐射的影响，太阳迫使直接照耀的纬度的空气以周期T_beat = 1 (年)的节拍做空气密度振荡。

(2) 太阳直接照耀的纬度上无风，风速为零

这是因为此处空气与太阳辐射之间是相长干涉(constructive interference)，这个直接照耀的纬度A₁被称为第一相长干涉脊(first constructive interference ridge)。把风速为零v_win = 0代入节拍周期公式，已知T_beat = 1 (年)，计算出脊上的太阳效应：

$v_{sun\text{\_}effect}=\text{369}\text{.788}-\omega r\cos \left(A_1\right);\left(\text{units}:\text{m}/\text{s}\right)$ (13)

其它维度上要考虑太阳辐射的倾斜因子，得到全球太阳效应为

$v_{sun\text{\_}effect}=\text{369}\text{.788}\cos \left(A-A_1\right)-\omega r\cos \left(A\right)$ (14)

(3) 风速公式

脊上风速为零，脊附近风速不为零。已知全球太阳效应，把v_{sun_effect}代入节拍周期公式，脊附近的纬度A的风速为

$v_{wind}=\sqrt{{\omega }^2{r}^2-\frac{4\pi c^3}{\beta T_{beat}}}-\omega r\cos \left(A\right)-v_{sun\text{\_}effect}$ (15)

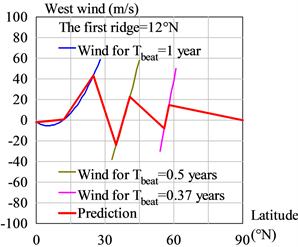
维持这些波的相长干涉条件并不容易。当第一个相长干涉脊位于北纬A₁ = 12˚N时，通过上述方程计算出在北纬A = 12˚N附近维持节拍T_beat = 1 (年)所需的风，如图8(a)蓝线所示。

(4) 第2脊和第3脊

随着维度A升高，第1脊被相消干涉(destructive interference)破坏，但是，满足相长干涉条件的下一个位置将再次出现。通过节拍公式的计算我们知道，在A = 39 N位置(第2脊)，节拍T_beat = 0.5 (年)；在A = 57˚N位置(第3脊)，节拍T_beat = 0.37 (年)，这是地球在北极区域内可以获得的最短时间周期。第2脊和第3脊附近的风速，如图8(a)所示。

(5) 北半球的风速曲线

最大风速出现在前两个脊的中点，约为48 (m/s)。连接图8(a)中的所有特征点，我们获得了北半球的预测的风速曲线；这一预测与海拔10 km (200 hPa)处的实验观测结果非常吻合 [14] ，如图9所示。木星上的纬向风具有相同的特征，如图7(b)所示。

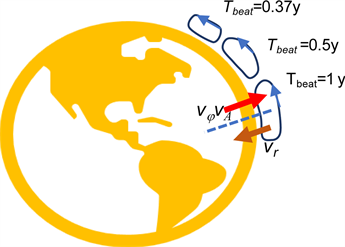(a) (b)

Figure 8. (a) Calculation of west winds in the northern hemisphere; (b) The atmospheric circulation in the northern hemisphere

图8. (a)北半球西风的计算结果；(b)北半球的大气环流

< Clet2020 Script > //C source code [9]

double beta,H,M,r,rc, rs, rot,v1,v2, Year,T,Lamda,V,a,b,w,Fmax,N[500],S[500],F[100]; int i, j, k, t, m, n, s, f,Type,x;

int main(){beta=1.377075e+14; H=SPEEDC*SPEEDC*SPEEDC/beta;

M=5.97237e24; rs=6.371e6; rot=2*PI/(24*3600); Year=24*3600*365.2422;

Type=1; x=10; if(Type>1) x=-30;//v2=rs*rot; a=v2*v2-4*PI*H/Year; V=sqrt(a)-v2;

if(Type==1)SetAxis(X_AXIS,0,0,90Latitude#n(°N);0;30;60;90;);

elseSetAxis(X_AXIS,-90,-90,90Latitude#n(°N);=90;-60;-30;0;30;60;90;);

SetAxis(Y_AXIS,-100,-100,100West wind (m/s);-100;-80;-60;-40;-20;0;20;40;60;80;100;);

DrawFrame(0x016a,Type,0xafffaf);//Polyline(2-90,0,90,0);

Check(15,k); if(k>24) k=24; if(k<-24) k=-24; //TextAt(100,10V=%f,V);

T=Year/2; Wind(); f=0; Findf(); t=N[m+m]; T=Year; Wind(); f=0; Findf();

SetPen(2,0xff); Polyline(n,N,x,70Wind for T#sdbeat#t=1 year); if(Type>1) Polyline(s,S);

F[0]=N[0];F[1]=N[1]; F[2]=N[m+m]; F[3]=N[m+m+1];t=(t+F[2])/2;//midst of two ridges

t=t-F[2]+m; Fmax=N[t+t+1]; //TextAt(100,20t=%d, Fmax=%f ,t,Fmax);

f=Fmax; Findf(); F[4]=N[m+m]; F[5]=N[m+m+1];

T=Year/2; Wind(); f=-Fmax/2; Findf(); t=m;f=Fmax/2; Findf();

SetPen(2,0x80ff00); Polyline(n,N,x,-50Wind for T#sdbeat#t=0.5 years); if(Type>1) Polyline(s,S);

F[6]=N[t+t]; F[7]=N[t+t+1];F[8]=N[m+m]; F[9]=N[m+m+1];

T=0.37*Year; Wind(); f=-Fmax/4; Findf(); t=m;f=Fmax/4; Findf();

SetPen(2,0x9933fa); Polyline(n,N,x,-70Wind for T#sdbeat#t=0.37 years); if(Type>1) Polyline(s,S);

F[10]=N[t+t]; F[11]=N[t+t+1];F[12]=N[m+m]; F[13]=N[m+m+1];F[14]=90; F[15]=0;

//Draw(ELLIPSE,0,2,XYX,1015,20,25,35);TextHang(5,40,0a route);

SetPen(3,0xff0000); Polyline(8,F,x,-90Prediction); TextHang(x,90,0The first ridge=%d°N, k);

}

Wind(){n=0;s=0;

for(i=0;i<90;i+=1){ a=i*PI/180; b=(i-k)*PI/180; v1=rot*rs*cos(a); v2=rot*rs;

w=369.788*cos(b)-v2*cos(k*PI/180); a=v2*v2-4*PI*H/T; V=sqrt(a)-v1-w;

if(V>-40 && V<60) {N[n+n]=i; N[n+n+1]=V; n+=1;}}

for(i=0;i<90;i+=1){ a=-i*PI/180; b=(-i-k)*PI/180; v1=rot*rs*cos(a); v2=rot*rs;

w=369.788*cos(b)-v2*cos(k*PI/180); a=v2*v2-4*PI*H/T; V=sqrt(a)-v1-w;

if(V>-40 && V<60) {S[s+s]=-i; S[s+s+1]=V; s+=1;}} }

Findf(){a=1e10; for(i=0;i

}//if(k==12) ClipJob(APPENDi=%d,V=%f,i,V);

#v07=?>A

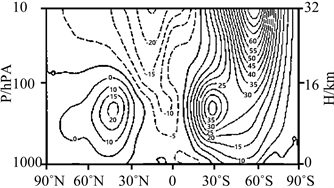(a) (b)

Figure 9. NCEP/NCAR data, mean west winds over 40 years (1958~1997) [14] ; (a) winter; (b) summer

图9. NCEP/NCAR数据，40年平均西风(1958~1997) [14] ；(a)冬季；(b)夏季

(6) 北半球的风速矢量

为了进一步提高精度，把上式计算得到的风速值分解为球坐标 $\left(r,A,\phi \right)$ 中的三个分量

$v_{wind}^2=v_r^2+v_A^2+v_{\phi }^2$ (16)

根据热力学中的能量均分定理，我们近似地得到它们的平均估计值

$\langle v_r^2\rangle =\langle v_A^2\rangle =\langle v_{\phi }^2\rangle =\frac{1}{3}{v}_{wind}^2$ (17)

因此，地球北半球的风速矢量如图8(b)所示，其中大气环流由三个单元组成：Hadley cell, Ferrel cell, arctic cell。

(7) 季节钟

节拍T_beat ＝ 1 (年)在热带地区产生出两季(旱季与雨季)。节拍T_beat = 0.5 (年)在欧洲、北美和东北亚吹出舒适的风，并调节出四季(春，夏，秋，冬)，这个节拍是一个广为人知的季节钟。北极地区喜欢整数的节拍T_beat = 1/3 (年)而不是节拍T_beat = 0.37 (年)，这种情形导致额外的冷气流。最短节拍T_beat = 0.37 (年)需要包含节拍T_beat = 1/3 (年)同时每2.24年向欧洲、北美洲和东北亚排放一次额外的冷气流 [15] ，它们被认为是行星尺度波或Rossby波。

(8) 赤道的东风(Easterlies)

由于空气的相对论性物质波与地壳的相对论物质波干涉，因此图8(a)中赤道的东风的数量级约为10 m/s。信风或东风是在地球赤道地区流动的永久性的东西向盛行风(prevailing winds)。

6. 人类生物钟

Figure 10. (a) A human sketch with the head pointing to the North Pole; (b) the biological clock

图10. (a)人体头朝向北极的示意图；(b)生物钟

人体由五个部分组成：一个头部和四肢，心脏将血液循环输送到全身。假设一个人睡在床上，头部指向北极，如图10(a)所示，心脏的五条红线代表其五条动脉血管。

显然，流入两臂的动脉血液的物质波会与地壳的物质波发生干涉，产生一种节拍现象：

$\begin{array}{l}{\left|\psi \right|}^2={\left|{\psi }_{blood}+C{\psi }_{shell}\right|}^2=1+C^2+2C\cos \left[\frac{2\pi }{{\lambda }_{beat}}{\displaystyle {\int }_L\text{d}l-\frac{2\pi }{T_{beat}}t}\right]\\ \frac{2\pi }{T_{beat}}\simeq \frac{\beta }{c^3}\left(\frac{v_{blood}^2}{2}-\frac{v_{shell}^2}{2}\right);\frac{2\pi }{{\lambda }_{beat}}=\frac{\beta }{c^3}\left(v_{blood}-v_{shell}\right);v_{shell}=\omega r\end{array}$ (18)

其中C表示耦合系数，w是地球的角速度，r是地球半径，地壳ψ_shell具有球对称性。血流速度随血管的位置而变化。成人主动脉瓣口血流速度正常值为1.0 m/s~1.7 m/s，儿童为1.2 m/s~1.8 m/s。颈动脉血流速度小于1.2 m/s，腹主动脉血流速度小于1.8 m/s，下腔静脉血流速度为5 cm/s~25 cm/s。因此，1 m/s是血流速度的数量级。假设人体手臂在心脏附近的平均血流速度为1 m/s，那么流动的血液会出现如下周期的节拍：

$\begin{array}{l}{v}_{shell}=r\omega =463.8\text{m}/\text{s};v_{blood}=v_{shell}\pm 1\text{m}/\text{s}\\ T_{beat}\simeq \frac{4\pi c^3}{\beta \left(v_{blood}^2-v_{shell}^2\right)}=\pm 84\left(\text{years}\right);{\lambda }_{beat}=1.2\text{e}+12\left(\text{m}\right)\end{array}$ (19)

< Clet2020 Script > // [9]

double beta,H,M,r,rc, rs, rot,v1,v2, Year,T,Lamda,V,a,b,x,y,w;

int main(){beta=1.377075e+14; H=SPEEDC*SPEEDC*SPEEDC/beta;

M=5.97237e24; rs=6.378e6; rot=2*PI/(24*3600); Year=24*3600*365.2422;

v1=rot*rs;v2=v1+1; a=v2*v2-v1*v1; T=4*PI*H/a;

T/=Year; Lamda=2*PI*H/(v2-v1); b=Lamda/(2*PI*rs);

TextAt(100,20v1=%f, v2=%f, T=%f, L=%e, b=%e,v1,v2,T,Lamda,b);

}#v07=?>A

事实上，血液从心脏被泵入图10(a)中的东臂和西臂，在两个臂中产生一个正拍和一个负拍，周期相同84年，这两个拍通过两个臂形成一个整体节拍。研究发现，人类的平均寿命仅限于单一节拍周期内，此节拍周期认定为人类生物钟。节拍波长l是地球周长的30,000倍，l的效应几乎没有观察到。

根据前述对ψ的解释，节拍 ${\left|\psi \right|}^2$ 表示在宏观尺度上发现核子的概率，换句话说 ${\left|\psi \right|}^2$ 与物质密度成比例。

${\left|\psi \right|}^2\propto \rho$ (20)

图10(b)中，节拍 ${\left|\psi \right|}^2$ 在一个节拍周期内的振荡代表了整个生命中人体密度的变化。人类生命中的骨密度(红线)和肌肉(蓝线)随着年龄的变化而变化，对应 ${\left|\psi \right|}^2$ 振荡，如图10(b)所示。航天员进入太空站后与地球自转的耦合降低，出现明显的骨密度下降，说明地球表面的正常人的骨密度与 ${\left|\psi \right|}^2$ 有强关联关系。

显然，人类的骨骼和肌肉在生命过程中是不可逆的，它们也完全阻止人类进入第二次节拍，以获得168岁的寿命。也许，一些柔软的动物或细胞可能会进入多节拍过程，以延长寿命或永生。睡眠姿势、行走、跑步、坐下等都可能在一定程度上影响人体生物钟，但不能停止人体生物钟的嘀嗒进程，因为血液就像生命一样永不停止。人体生命过程是由许许多多的瞬时活动积累而成，那么计算人体寿命T的积累公式为

${\displaystyle {\int }_0^T\frac{F\left(C\right)\text{d}t}{T_{beat}\left(t\right)}}={\displaystyle {\int }_0^T\frac{F\left(C\right)\beta \left(v_{blood}^2-v_{shell}^2\right)}{4\pi c^3}\text{d}t}=1$ (21)

其中F(C)是瞬时耦合系数C的函数。

这个公式也可以用来估算动物寿命。百度百科“动物寿命”词条 [16] 中列举了一些长寿生物，例如，英国芬得克里夫兰郡的地下发现的“玛士撒拉小虫”2.6亿岁；名为“明”的蛤类507岁；欧洲博物史中曾记载的狗鱼267岁；英国利物浦名叫“詹米”的亚马孙鹦鹉104岁；美国佐治亚州黑猩猩名为珈玛59岁；澳洲的哈丽(Harriet)龟，估计约175岁。本文的寿命公式可以覆盖这些长寿动物例子。

可以从两个方面来理解 ${\left|\psi \right|}^2$ 。(1) 生物细胞如何感知 ${\left|\psi \right|}^2$ ？如我们所知， ${\left|\psi \right|}^2$ 表示核子在宏观尺度上出现的概率。可以把它比作一个气球，如图11所示，气球上的三个黑点代表生物细胞的三个分子。当气球或ψ膨胀时，生物细胞的三个分子之间的空间变大，从而削弱了它们之间的结合力。当气球或ψ收缩时，生物细胞的三个分子之间的空间变小，从而它们之间的结合力增加。因此，生物细胞可以感知ψ的变化。(2) ψ的统计特性。“大气循环与季节钟”一节中指出风是一种量子引力效应。如果我们观察日常生活，我们看到一阵风又一阵风，风表现无常。但是美国NCEP/NCAR四十年的观察记录显示地球表面存在固定的风场。所以，风是一种统计学上看到的量子引力效应。同样，生物钟也是一种统计学上看到的量子引力效应。

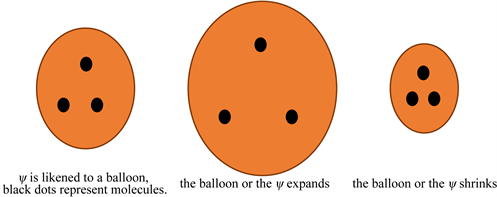
Figure 11. The ψ as if a balloon, the three dark dots represent tree molecules of a biological cell

图11. 可以把ψ比作一个气球，气球上的三个黑点代表生物细胞的三个分子

7. 生物钟的抗衰老指南

在前一节中，我们推导了人类生物钟的公式。可以看出，增加人体心脏附近的平均血流速度将导致寿命减少；降低人体心脏附近的平均血流速度将导致寿命延长；瞬时耦合系数C也是一个重要的影响因素。为了追求延长寿命或抗衰老，以下是一些参考意见。

(1) 睡觉姿势

首先，头部需要指向北极，这样身体各个部位的血流速度在地球自转方向上的投影分量相对较小，有利于生命的延长。其次，与伸展四肢的姿势相比，侧卧也减少了血流速度在地球自转方向上的投影分量，如图12(a)所示。

Figure 12. Lying-stretched out, lying on a side with the head pointing to the North Pole; (b) facing the sun

图12. (a)身体伸直，侧卧，头部指向北极；(b)面向太阳

(2) 药物

毫无疑问，有些药物可以调节人体各个部位的血流速度。通常情况下，喝茶、咖啡、酒精等会在一段时间内增加人体内血液的流动速度，从而导致减少寿命的累积效应。明矾等亲水性化合物可以降低身体各个部位的血流速度，但也会对生命体产生副作用和毒性例如痴呆。

增加氧气可以减少呼吸频率和降低血流速度，海拔越高氧气越稀薄，所以居住在低海拔高度的居民比居住在高海拔高度的居民寿命较长。例如，中国2021年的统计显示，沿海城市上海人均寿命84.11岁 [17] ；高原地区青海省人均寿命73.97岁 [18] ，高原地区云南省人均寿命74.4岁 [19] 。血管支架可以显著增加孔径和降低血液流速，2021年1月至2022年11月全国集采的冠脉支架采购量为498万个 [20] ，北京、上海等大城市使用量较大，这与大城市居民长寿的关系有待密切观察。

正如我们所知，一些中国传统草药可以降低人体血液流速，且毒性较小，事实上，古代中国人不知道草药是如何工作的，今天我们从人体生物钟方面理解了它。

(3) 办公室时间

在中国，程序员、文员、教师等上班族每天在办公室呆8小时。为了削弱人体内血流速度与地球自转之间的耦合效应，以延长人类寿命，上班族人员在端坐几个小时期间需要面朝太阳(东或西)，如图12(b)所示。还建议上班族人员喝冷水和吃冷食物。

(4) 建筑与环境

几乎所有人的一生都在房间或建筑物中度过，建筑和环境都对人类的一生有很大的影响。需要根据量子引力理论 [21] [22] 做出许多努力，以使这些建筑与环境有益于人类活动。

(5) 移民到其它行星与寿命减少

对于火星、木星、土星、天王星、海王星，它们的参数(β，等)收集在参考文献 [6] 中。不管它们的大气层如何，使用上面的节拍周期公式，计算出这些行星上的人类生物钟，结果如下：火星8.6年；木星10.6年；土星7.3年；天王星1.04年；海王星0.96年，计算的源程序如下。没有人会对这些星球上的寿命减少的生活感到满意；移民到火星总是停留在我们的幻想中。另外，地球的β参数是根据月球轨道计算得出的，要维护好人类生物钟就要以要保护好月球。

< Clet2020 Script > // [9]

double ABeta[10]={ 2.961520e+10, 1.377075e+14 , 2.581555e+15, 4.016793e+13, 7.183397e+13, 1.985382e+15, 2.077868e+15,};

double Ar[10]={1, 1,0.5326, 11.209, 9.449, 4.007, 3.882,};

double AD[10]={1, 24, 24.6,9.9, 10.35,17.25, 16.1,};

int i,j; double beta,H,M,r,rs,rot,v1,v2, Year,T,Lamda,a,b,d;

int main(){j=50; rs=6.378e6; Year=24*3600*365.2422;

for(i=1;i<7;i+=1) {

beta=ABeta[i]; H=SPEEDC*SPEEDC*SPEEDC/beta; r=Ar[i]*rs; d=AD[i];

rot=2*PI/(d*3600); v1=rot*r; v2=v1+1; a=v2*v2-v1*v1; T=4*PI*H/a;

T/=Year; Lamda=2*PI*H/(v2-v1); b=Lamda/(2*PI*r);

TextAt(100,jv1=%f, v2=%f, T=%f, L=%e, b=%e,v1,v2,T,Lamda,b);

j+=30;}

}#v07=?>A

8. 结论

研究发现，相对论物质波为人类提供了一个生物钟。本文首先给出了两个例子来展示相对论物质波的有效性。其次，对太阳黑子周期、地球大气环流和人类生物钟进行了研究，推导出了钟公式。结果表明，太阳黑子周期为10.93年，人类平均年龄为84岁，为生物钟设计了抗衰老指南。

参考文献