1. 引言
近年来,随着学者们对压电智能材料的不断深入研究,压电材料在振动控制领域的应用越来越广泛 [1] [2] [3] [4] 。文献 [5] 最早利用压电材料开展了梁的振动控制研究。
压电振动控制的分析方法主要有有限元法 [6] 、解析法 [7] 以及半解析法 [8] 等。基于压电材料进行主动控制,主要是通过在结构上粘贴压电单元,通过压电“电–力”转换产生的力来抑制振动,该方法能够较好地适应外部环境的变化,可以积极抵消外部环境振动。
本文将分别对悬臂板、四边固支板及低频隔振基台进行压电振动控制研究,并在有限元环境,研究并提出适用的压电振动控制方法。
2. 悬臂板压电振动控制
首先对某悬臂板进行压电振动控制研究,该板左侧固定。悬臂板为铝板,长度、宽度及厚度分别为504 × 25.4 × 0.8 mm,压电作动器贴片的尺寸为72 × 25.4 × 0.61 mm。铝板的弹性模量为6.8 × 1010 N/m2,泊松比0.32,密度2800 kg/m3;压电材料PZT-5H [9] 的密度为7500 kg/m3,恒定电场下的弹性刚度矩阵为:

压电应变矩阵为:
介电常数矩阵为:
悬臂板端部位置作用一个幅值0.1 N的竖向阶跃荷载。
数值计算采用ANSYS有限元分析软件,悬臂板采用solid 45单元模拟,压电作动器采用solid 5单元模拟。
仅考虑上部粘贴压电片的悬臂板振动控制模型如图1所示。

Figure 1. Cantilever plate structure with piezoelectric sheet pasted on the upper side
图1. 上部单侧粘贴压电片的悬臂板结构
压电振动控制是以控制悬臂板上的4、6号节点的x向应变为目标,即[ux(4) − ux(6)]/dx,受文献 [10] 启发,本研究中压电片输入电压的控制设计为:
err = 0 – ks × [ux(4) − ux(6)]/dx,va = kc × kv × err,其中,ux为获取节点的x向位移,err为应变偏差,ks为增益系数,取1 × 103,kv为增益系数,取1 × 103,kc为增益系数,分别取0,0.1,0.5,dx为两节点间的水平距离,dx = 0.012,va为控制电压。
图2给出悬臂板端部中点位置的竖向变形曲线,可见,当kc = 0.5时,悬臂板的振动控制效果显著,明显优于无控制状态(kc = 0),且优于kc = 0.1的控制状态。压电片的控制电压如图3所示。
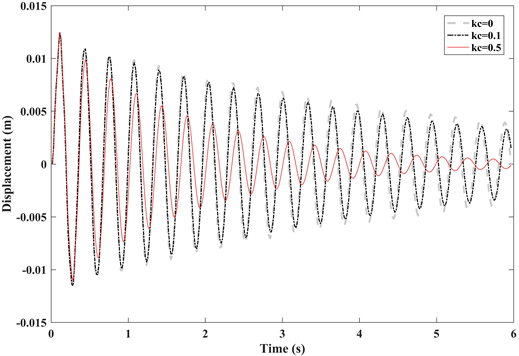
Figure 2. Tip response of cantilever plate structure with piezoelectric sheet pasted on the upper side
图2. 仅上部粘贴压电片的悬臂板端部响应

Figure 4. Cantilever plate structure with piezoelectric sheet symmetrically pasted on the upper and lower side
图4. 上、下部对称粘贴压电片的悬臂板结构
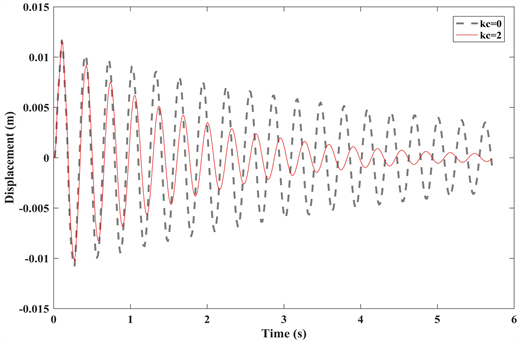
Figure 5. Tip response of cantilever plate structure with piezoelectric sheet symmetrically pasted on the upper and lower side
图5. 上、下部对称粘贴压电片的悬臂板端部响应
考虑上、下部对称粘贴压电片的悬臂板振动控制模型如图4所示。图5给出悬臂板端部中点位置的竖向变形曲线,可见,当kc = 2时,悬臂板端部的振动控制效果显著,明显优于无控制状态(kc = 0)。
3. 四边固支板压电振动控制
在对悬臂板压电振动控制研究的基础上,开展四边固支薄板的压电振动控制。薄板为铝板,铝板长、宽、厚分别为305 × 25.4 × 0.8 mm,压电作动器贴片的尺寸为20 × 20 × 1 mm。固支板跨中位置作用一个幅值0.1 N的竖向阶跃荷载。板采用shell63单元模拟,压电作动器采用solid 5单元模拟。考虑薄板上部跨中布置压电作动器,模型如图6所示。


Figure 6. Four-side fixed plate with piezoelectric sheet pasted on the upper part
图6. 上部粘贴压电片的四边固支薄板
压电振动控制是以控制悬臂板上的2453、2461号节点的x向应变为目标,即[ux(2453) − ux(2461)]/dx,控制过程为:
err = 0 – ks × [ux(2453) − ux(2461)]/dx,va = kc × kv × err,ks取1 × 103,kv取1 × 103,kc分别取0,0.2,dx = 0.0039。
图7给出固支薄板中点位置的竖向变形曲线,可见,当kc = 0.2时,薄板的振动控制效果明显优于无控制状态(kc = 0)。
4. 低频隔振系统压电振动控制
对于诸如气浮型的低频振动控制系统,在微振动控制领域应用较为广泛,被动式的低频隔振系统虽能够隔离较大频带范围内的环境扰动,但对于较低频成分的控制效果不理想,所以,往往需要附加主动控制。
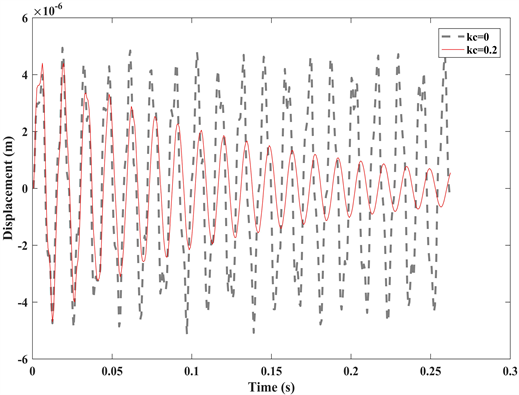
Figure 7. Midpoint response of four-side fixed plate with piezoelectric sheet pasted on the upper part
图7. 上部粘贴压电片的四边固支薄板中点响应
接下来,将在对悬臂薄板以及四边固支薄板进行压电振动控制研究的基础上,开展低频隔振系统的压电振动控制研究。
某隔振基台,长、宽、厚分别为1 m、1 m、0.1 m;弹性模量6.8 × 1010 N/m2,泊松比0.32,密度2800 kg/m3,基台采用solid 45单元模拟,压电作动器采用solid 5单元模拟,有限元模型如图8所示。
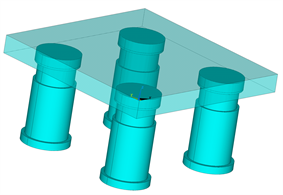
Figure 8. Finite element model of low-frequency vibration isolation system
图8. 低频隔振系统有限元模型
基台上部中间位置作用一个幅值0.1 N的竖向阶跃荷载。隔振基台竖向设计频率为1 Hz,水平及竖向考虑0.15的阻尼比。在隔振基台下部中间位置粘贴压电作动器,压电片的尺寸为100 × 100 × 1 mm。
压电振动控制是以控制基台上的150、151号节点的z向应变为目标,即[uz(151) − uz(150)]/dx,err = 0 – ks × [uz(151) − uz(150)]/dx,va = kc × kv × err,其中,ks = 1 × 103,kv = 1 × 103,kc分别取0,25,50,dx = 9.5 × 10−4。
图9给出基台中点位置的竖向变形曲线,可见,kc = 50时,基台的振动控制效果明显优于无控制状态(kc = 0),且优于kc = 25的控制状态。
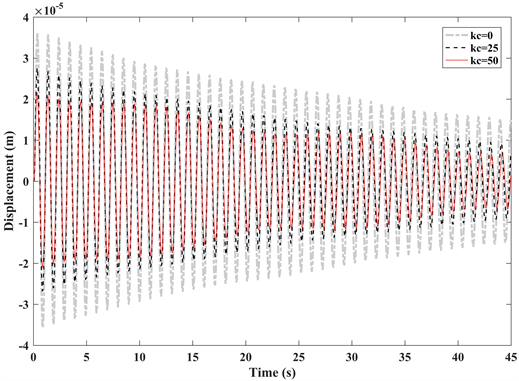
Figure 9. Piezoelectric vibration control response of low-frequency vibration isolation system
图9. 低频隔振系统压电振动控制响应
5. 小结
本文对悬臂板、四边固支板及低频隔振系统开展了较为系统的压电振动控制研究,并在有限元环境,进行了压电控制电压的输入设计。数值计算结果表明,采取的压电振动控制方法,对于以上三种结构的振动控制效果显著,验证了所提压电振动控制方法的有效性。
本研究对于工程结构压电振动控制具有指导意义,特别是对于低频隔振系统的压电振动控制,具有重要的现实意义,实际工程中,可基于本研究,面向气浮等低频振动控制系统,附加压电智能材料,进行主动控制。
基金项目
国机集团科学技术研究院有限公司青年基金项目“高层建筑实验室集群多源振害控制及运维监测关键技术研究与应用”;中国机械工业集团青年基金重点项目“大科学工程群微纳级环境振动控制关键技术研究与应用”;中国机械工业集团重大技术开发专项“建筑与装备工程振震双控关键技术研发及应用示范”。