1. 引言
耦合振子系统的振荡猝灭(oscillation quenching)现象是指耦合动力学系统通过系统内相互作用或在外界环境影响下,子系统停止各自的振动行为,使得各个子系统的状态变量不再随时间变化,稳定到各种类型的固定点上的动力学行为。最早发现并记录振荡猝灭现象的是英国物理学家Lord Ray Leigh,他发现相邻的管风琴的管子会因相互作用而消音 [1] ;后来人们先后在各类非线性耦合系统中都发现了振荡猝灭现象,并且相继在各种实验中(电子电路系统 [2] 、化学振子 [3] 、生态系统 [4] 、耦合神经元振子 [5] [6] )观察到了这种振荡猝灭现象。近年来,根据振荡猝灭的产生机制和最终稳态的表现,振荡猝灭可分为振幅死亡(amplitude death,简称AD)和振荡死亡(oscillation death,简称OD)两种形式。振幅死亡一般指全部振子被吸引到同一个不动点上,根据不动点的不同,振幅死亡又分为平凡振幅死亡(不动点为零点)和非平凡死亡(不动点非零点)。振荡死亡是指系统会出现两个或两个以上的新的不动点,而这些新的不动点的产生是由振子相互作用使得系统固有不动点出现对称性破缺造成的 [7] [8] 。
对于现实生活中许多自然或人造系统来说,维持稳定且有节奏的活动是其正常运作和演化的先决条件。而振荡淬灭可能会使这些系统的功能遭受巨大破坏,大幅度降低它们的性能,严重时甚至会使系统部分崩溃乃至完全崩溃。例如,哺乳动物的心室颤动可能会导致心脏骤停,这就是一种人体心脏和呼吸系统的振荡猝灭现象,而这可能会引起起搏细胞的固有功能丧失从而导致呼吸困难甚至危及生命 [9] ;脑电波系统中的振荡猝灭通常会造成部分大脑功能的暂时丧失 [10] ,严重时甚至会导致脑死亡 [11] ;有研究表明,振荡猝灭现象与阿尔茨海默病和帕金森病这两种常见的神经退行性疾病的产生密切相关 [12] ;在电网的电力传输系统中,当发电机中发生振荡猝灭现象时,可能导致发电系统的崩溃从而大规模停电 [13] 。因此,一旦现实系统意外出现振荡猝灭,陷入静止状态,人们就需要提出合适的策略来尽快复苏系统从而减少不必要实际损失。例如若可以研究清楚振荡猝灭现象与阿尔茨海默病和帕金森病这两种常见的神经退行性疾病的内在机制和关联,那么就可以通过压制某些不需要的振荡状态对这些疾病进行控制治疗,帮助患者恢复正常 [14] 。近些年,为了复苏意外出现振荡猝灭现象的系统,国内外众多专家学者们都针对克服振荡猝灭现象作了深入的研究,提出很多有效的方法策略。在2010年,Zou等人首先提出利用梯度耦合消除时滞造成的振荡猝灭现象,开创了研究振荡复苏策略的先河,随后Zou和他的合作者又提出梯度耦合 [15] 、处理延迟 [16] 、反馈因子 [17] 、低通滤波器 [18] 来消除振荡淬灭现象。Yadavet等人发现共同环境耦合方案也可以有效恢复振荡,这为抑制神经系统的某些干扰和通过离子通道控制神经元尖峰提供了可能 [19] 。
振荡猝灭可以看成是系统以最终稳态为对称轴达到了某种意义下的对称平衡。而不对称因子可以破坏系统的对称性,因此在2017年,Zhao等人提出在耦合系统中引入不对称因子,仅仅通过调整不对称因子就可以有效地恢复耦合振子系统的振荡 [20] ;此外,利用反馈作为一种控制,已经成为实现预期目标或状态的重要思想 [21] [22] [23] 。实际上,当反馈加入耦合系统时,可以看作是向系统新增一个外力。如果反馈是正的,它可以刺激振子偏离平衡,从而可以用来打破系统的稳定状态。如果反馈是负的,它通常可以抑制系统的无序行为,从而帮助系统达到稳定状态 [24] 。2015年,Chandrasekar等人证明了反馈对于恢复系统振荡具有普遍适用性 [25] 。2020年,Zhao等人提出通过平均场反馈克服振荡猝灭,不用考虑系统本来的耦合情况,也不需要调整内在参数或耦合方案,单纯增加反馈强度就可以显著恢复振荡猝灭状态下的系统振荡,显著提高了复苏策略的实际应用性 [26] 。受此启发,本文将平均场反馈扩展到更一般的形式,即使用双权重反馈作用于系统的每个振荡器,并试图找到一个更好的权重值来恢复耦合系统的振荡。
本文的结构如下:在第二部分,我们讨论了耦合Stuart-Landau系统中振荡器频率相同时不同权重的作用。通过理论分析和数值模拟发现,发现在大多数系统中当两个权重同时为0或1时效果最好,这意味着我们只需要寻找最易得到信息的振子,将其作为反馈加到该振子上,就能简单便捷的恢复不同死亡状态下的系统振荡。而在实际系统中最易得到信息的振子一般也是最易添加反馈的振子。在第三部分,考虑了双权重在振荡器频率不同的情况下的影响。最后,本文以第四部分中的总结作为结尾。
2. 具有相同频率的耦合Stuart-Landau振荡器
2.1. 消除时间延迟耦合场景中的AD
我们利用Stuart-Landau耦合振子模型,研究双权重反馈对打破系统死亡状态的有效性,并将其作为研究系统复苏的范例模型探讨权重对系统复苏的影响。
首先,讨论具有两个频率相同的时滞耦合Stuart-Landau振子:
(1)
上述耦合系统(1)表示双权重反馈耦合系统。其中
表示双权重反馈的权重,
表示复振幅,
表示振荡器的固有频率,每个孤立振子j的半径均为1,且保持频率为
的极限环振荡。在模型中,K控制耦合强度,
表示时间延迟,
表示反馈强度,这是诱发AD的经典方法 [2] 。
当
时,双权重反馈就是平均场反馈,在这里我们运用线性稳定性分析来探究
和
时系统(1)所对应雅克比行列式的特征值。
(2)
当特征值的实部都小于零时,系统达到稳定,即进入振荡淬灭态。因此,特征值实部的最大值越大,系统的AD区域就会越小,反馈消除振荡猝灭的效果就越好。从公式(2)中我们可以发现
或1时对应特征值的实部小于
即平均场反馈的实部,这说明选择单个振子作为反馈并将其作用于该振子从而恢复系统振荡的效果将优于平均场反馈的效果。为了更加直观的说明,我们分别在图1(a)~(e)中画出了当
和
时系统对应的AD区域,这里固有频率为
。不难发现
和
所对应的死亡区域远小于
,
和
所对应的死亡区域。
和
代表作为反馈项的振子和最终反馈所作用的振子是同一个振子。而在实际中,最易获取振子信息的振子和反馈最易作用于其上的振子通常是同一个振子,因此实验结果证明,双权重反馈在两个权重同时为1或0时,即用单个振子作为反馈作用于这个振子本身时,效果最好,并且减少反馈所需信息的同时还大幅降低将反馈加到系统中的难度。
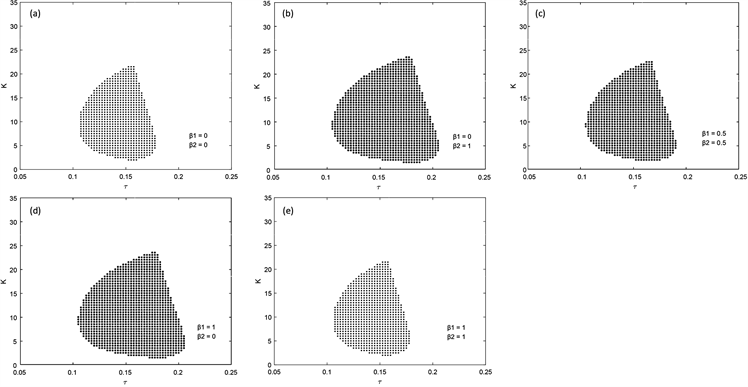
Figure 1. The AD domains of time delay system with given weight
and
图1. 给定权重
和
后时滞系统所对应的AD区域面积
2.2. 在共轭耦合和动态耦合场景中消除AD
考虑到共轭耦合(振子之间通过不同变量的耦合)和动态耦合(振子之间通过附加变量的耦合)也是耦合振子模型中产生各种现象的两个重要策略 [27] [28] 。下面讨论双权重反馈在两个共轭耦合Stuart-Landau振子中的影响:
(3)
和两个动态耦合Stuart-Landau振子中的影响:
(4)
同样的,我们直接探究
和
时系统(3)所对应雅克比行列式的特征值:
(5)
从公式(4)中我们可以发现
或1时,对应特征值的实部小于
即平均场反馈的实部,这说明选择单个振子作为反馈并将其作用于该振子恢复系统振荡的效果将优于平均场反馈的效果。而系统(5)所对应的雅克比行列式特征值难以计算,因此我们直接通过数值模拟来研究。
为了更加直观的说明,我们分别在图2(a)~(e)和图3(a)~(e)中画出了当
和
时系统(3)和(4)对应的AD区域,这里固有频率分别为
和
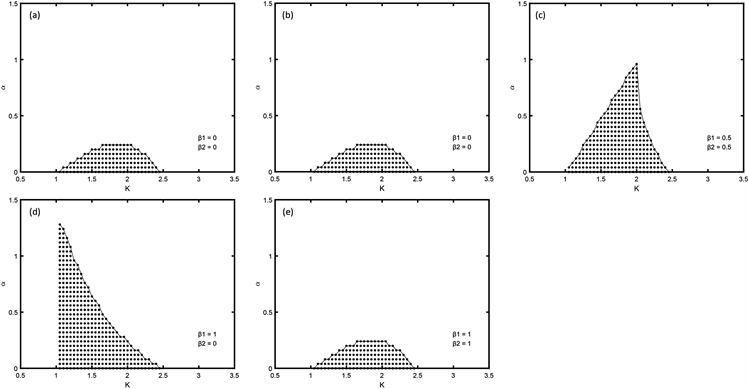
Figure 2. The AD domains corresponding to the conjugate coupled system with given weight
and
图2. 给定权重
和
后共轭耦合系统所对应的AD区域面积
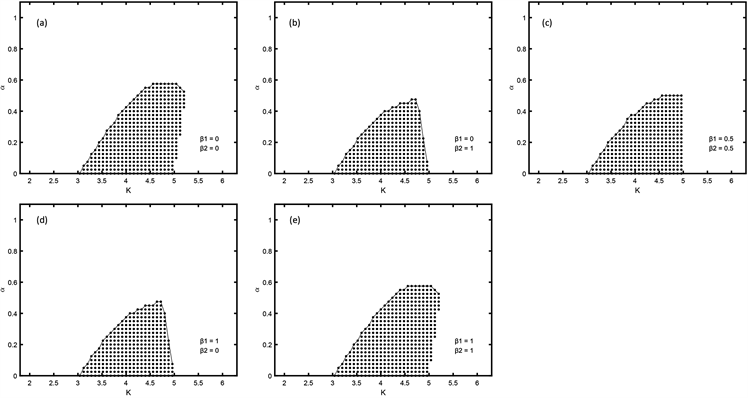
Figure 3. The AD domains corresponding to the dynamic coupling system with given weight
and
图3. 给定权重
和
后动态耦合系统所对应的AD区域面积
。不难发现对于共轭耦合系统(3),
和
所对应的死亡区域远小于
和
所对应的死亡区域。而对于动态耦合系统(4)
和
所对应的死亡区域则会略大于
和
所对应的死亡区域,但是都小于
即平均场反馈所对应的死亡区域。因此实验结果证明,对于频率相同的共轭耦合双权重反馈在两个权重同时为1或0时,即用单个振子作为反馈作用于这个振子本身时,效果最好,并且减少反馈所需信息的同时还大幅降低将反馈加到系统中的难度。对于频率相同的动态耦合双权重反馈在两个权重一个为0另一个为1时,即用单个振子作为反馈作用于另一振子时,效果最好,这可能是由动态耦合本身的不对称性造成的。
3. 具有不同频率的耦合Stuart-Landau振荡器
3.1. 消除参数不匹配耦合场景中的AD
前面我们讨论了双权重反馈对恢复频率相同系统振荡的作用,现在讨论双权重反馈对恢复频率不同的系统振荡的作用。
首先,讨论具有不同频率的耦合Stuart-Landau振荡器:
(6)
上述耦合系统(6)表示双权重反馈耦合系统。其中
表示振荡器的固有频率,每个孤立振子j的半径均为1,且保持频率为
的极限环振荡,此时我们将频率差值设置较小,且系统振幅较大。根据Premraj等人的研究 [29] ,当较小的频率差值和时滞同时出现时,耦合的Stuart-Landau系统中不会出现死亡区域。因此我们假设不存在时间延迟,即
。同样的,我们直接探究
和
时系统(6)所对应雅克比行列式的特征值:
(7)
从理论上很难比较特征值的大小,因此我们通过数值模拟做了相关实验。为了更加直观的说明,我们分别在图4(a)~(e)中画出了当
和
时系统对应的AD区域,这里频率差值为
。不难发现
和
时所对应的死亡区域远小于
和
所对应的死亡区域。因此实验结果证明,对于频率不同的系统,双权重反馈在两个权重同时为1或0时,即用单个振子作为反馈作用于这个振子本身时,效果最好,且减少反馈所需信息的同时还大幅降低将反馈加到系统中的难度。
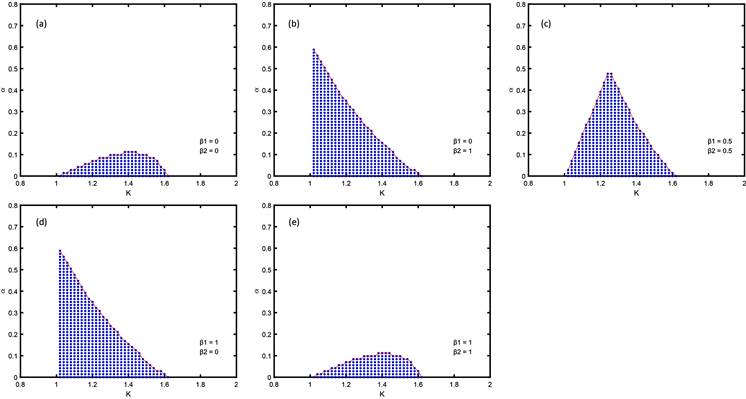
Figure 4. The AD domains corresponding to the parameter mismatch coupling system with given weight
and
图4. 给定权重
和
后参数失配耦合系统所对应的AD区域面积
3.2. 消除频率不同时共轭耦合场景中的AD
在本节中,讨论具有不同频率的共轭耦合系统:
(8)
用理论分析系统(8)时,发现很难求出系统对应雅克比行列式特征值和死亡区域对应条件,因此我们通过数值模拟对系统(8)进行了一些研究。为了更加直观的说明,我们分别在图5(a)~(e)中画出了当
和
时系统对应的AD区域,此时设定
。不难发现
和
所对应的死亡区域远小于
和
所对应的死亡区域。因此实验结果证明,对于频率不同的共轭耦合系统,同样是在两个权重同时为1或0时,即用单个振子作为反馈作用于这个振子本身时,效果最好。
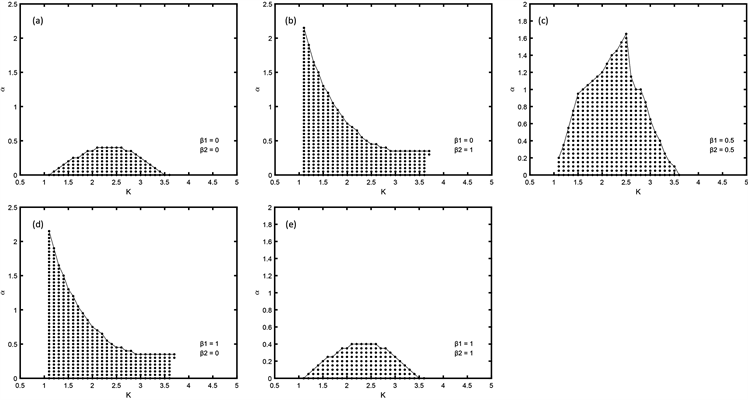
Figure 5. The AD domains corresponding to the parameter mismatch coupling system with given weight
and
图5. 给定权重
和
后参数失配耦合系统所对应的AD区域面积
3.3. 消除对称破损耦合场景中的AD和OD
双权重反馈不仅能够克服振幅死亡(AD)和振荡死亡(OD),而且还能克服系统从AD到OD的过渡。在前文中我们提到对称破损Stuart-Landau耦合系统是探索AD和OD状态演化转换的经典模型[8]。在此我们讨论对称破损Stuart-Landau耦合系统:
(9)
其中,
,频率
,
。正如Koseska在2013年所提到的,上述频率可以确保AD和OD在对称破损耦合系统中一起出现 [8] 。
双权重反馈当
和
时消除AD和OD的效果如图6(a)~(e)所示,此时反馈强度统一设置为
,蓝色部分代表AD,棕色部分代表OD。如图6(a)所示,在双权重均为零时(
),可以看到此时系统恢复振荡,没有振荡猝灭区域,AD和OD均被消除。而如图6(b)~(e)所示,当
和
时,可以看到此时系统中同时存在AD和OD,AD通过叉式分叉转换为OD,然后恢复振荡,图6(b)~(d)中的死亡区域相差不大,但都比图6(e)中的死亡区域小。对比五个图可以发现,以第二个振子作为反馈加到第二个振子上恢复系统振荡的效果最好,远远优于其他四种情况。
尽管我们无法通过理论证明选择哪个振子可以使恢复系统振荡的效果达到最好,但根据数值模拟可以发现,选择频率更高的振子可以更好的恢复系统振荡。此现象背后所蕴含的内部机理,和如何通过理论指导选择合适的振子作为反馈项以及将反馈最终加到哪个振子上,是一项值得学者们继续深入探讨的重要研究。
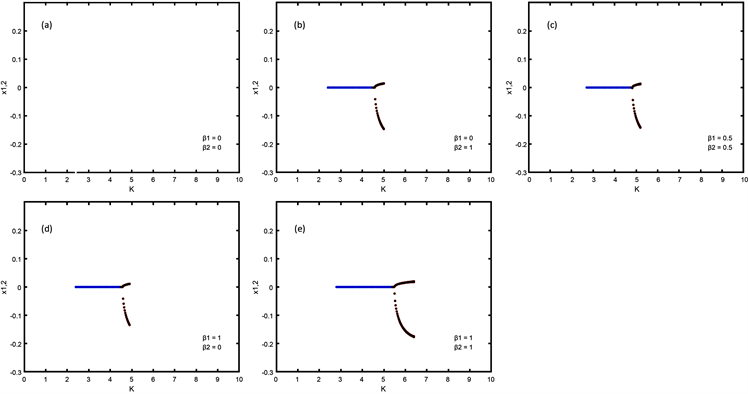
Figure 6. The AD and OD domains corresponding to the symmetry-breaking coupling system with given weight
and
图6. 给定权重
和
后对称破损耦合系统所对应的AD和OD区域面积
4. 结论
由于反馈对于恢复系统振荡具有普遍适用性且相对简单易行,故利用反馈克服振荡猝灭受到了诸多专家学者的关注,但在之前的研究中,反馈策略依然存在一些可以改进的地方,一方面,在之前的策略中反馈项通常是由多个系统振子组合而成的,而在实际模型中有些振子位于整个系统内部或被其他振子所掩盖,这些振子的相关信息是很难获得的;另一方面,之前的策略通常是将反馈项加到所有振子上,而在实际模型中想要将相同强度的反馈同时加到所有振子上是一件困难的事情,在将反馈加到位于系统内部的振子上时,时间延迟和强度损耗是难以避免的,而时间延迟又是影响系统振荡猝灭的主要原因之一。基于上述原因,在本文中我们提出了双权重反馈,最终发现,当权重同时为0或者为1时效果最好,这意味着我们只需寻找最易得到信息的振子,将其作为反馈加到该振子上,就能简单便捷的恢复不同死亡状态下的系统振荡。而实际模型中,最易得到信息的振子和最易添加反馈的振子大概率为同一振子,因此本策略减少反馈所需信息的同时还降低了反馈所需难度,这将有效提高本策略的实际应用性。
基金项目
中央高校基本科研业务费资助项目(自然科学类) (批准号:300102122113)。