1. 引言
江南地区人口稠密,经济发达,但也因为地理原因,受到副热带季风东亚热带季风的影响,每年夏季都会有一段持续时间的降水,又被称为梅雨季节,每年的梅雨季节都有可能会发生洪涝灾害。江苏省南京市就位于江南地区,梅雨季节集中在每年的6~7月。针对梅雨季节的降水情况,尤其是暴雨天气进行预测,以预测可能到来的洪涝灾害有着极为重要的经济价值和应用价值。
随着社会信息化的发展,目前国内外越来越多的研究选择使用计算机手段来进行有关天气要素特征的预测和分析。赵琳娜等利用贝叶斯模型平均方法,得到具有预测性的概率密度函数,然后采用EM算法,对淮河流域2008年7月1日~8月5日的降水数据预报进行了集成与订正 [1] 。史达伟等选择了机器学习中的分类与回归树算法、支持向量机算法、线性支持向量机算法、类支持向量机算法与类神经网络算法对连云港地区2014~2016年间大雾天气背景下发生特强浓雾天气的气象要素建立诊断模型,并发现这几种算法中,线性支持向量机算法的测试效果最好,但相较而言,决策树模型更加直观准确,且具有较高的泛化能力,综合效果更优 [2] 。张远汀等利用决策树算法,根据2017年12月~2018年2月和2007年12月~2008年2月国家测站日值数据中的各个气象要素,生成了一个二元判别决策树模型,用以预测当天是否会有积雪,但也有不足之处,此模型对于极端积雪天气的预测误差较大 [3] 。阮成卿等对影响华北地区汛期降水的年际分量的预报因子的强度进行逐年分类,针对每个分类都进行相应预报模型设计,利用条件降尺度法和偏相关预报因子挑选法,对原有的降水时间尺度分离模型进行改进,建立条件降水时间尺度分离统计降尺度模型,显著提高了预测准确率 [4] 。
朴素贝叶斯算法是一种应用广泛的分类预测算法。Mccallum A等使用多变量伯努利模型和多项式模型对文本进行分类,并发现多项式模型效果更好 [5] 。任民宏等利用朴素贝叶斯算法对大盘指数的涨跌进行预测。Rish I使用蒙特卡罗模拟法,系统研究了几个分类问题,发现朴素贝叶斯分类算法的准确性与特征向量之间的互信息的依赖程度并不直接相关 [6] 。Kohavi R提出了朴素贝叶斯和决策树算法的混合算法:朴素贝叶斯树(NBTree)算法 [7] 。Peng F等提出了一个广义的朴素贝叶斯模型——增强型朴素贝叶斯分类器(CAN),相较于原本的朴素贝叶斯模型,CAN放松了条件独立性假设,还能够直接运用来自统计语言建模的复杂平滑技术 [8] 。张文钧等提出一种双层的贝叶斯模型,结合随机森林和朴素贝叶斯算法,对文本进行分类 [9] 。黄宇达等对朴素贝叶斯和决策树算法进行了改进,引入了客观属性重要度这一参数,弱化了朴素贝叶斯必须的条件独立性假设,选用加权信息熵作为分类标准,得到的算法模型能够在一定程度上克服决策树算法原有的多指偏向问题 [10] 。邸鹏等改进了经典朴素贝叶斯分类算法,选择引入一个放大系数,从而降低先验概率的影响,扩大后验概率的权重 [11] 。李冬梅等选用UCI数据集,采用10倍交叉验证法,把概率优化函数代入至朴素贝叶斯中,利用朴素贝叶斯与决策树混合分类法,既避免朴素贝叶斯易下溢与过度拟合的问题,也降低了决策数算法过度拟合的可能,对冠心病医辅助诊疗系统起到了有效作用 [12] 。蒋良孝提出了基于支持向量机的朴素贝叶斯分类算法。任民宏等利用朴素贝叶斯算法对大盘指数的涨跌进行预测 [13] 。
但是,朴素贝叶斯模型有着一个极大的限制条件,它要求所有的特征属性必须相互独立,这一要求在现实生活中不仅几乎难以实现,有些特征属性之间还会有着较强的相关性。由此,贝叶斯网络模型这一算法进入了人们的视线。宫秀军等利用主动学习这一方法,通过修正分类参数,提出了一种主动贝叶斯分类模型 [14] 。吴立增等基于贝叶斯网络模型建立了变压器的TAN故障诊断模型和朴素贝叶斯网络故障诊断模型 [15] 。陈雪等基于贝叶斯网络分类算法实现了对遥感影像的变化的检测 [16] 。
因此,本文选择了更高等级,应用范围也更广的贝叶斯网络模型来对南京市梅雨季节的降水情况进行相关的诊断分析。
2. 贝叶斯分类模型
2.1. 贝叶斯网络
贝叶斯网络(Bayesian network),又称为信度网(Belief Network, BN)或有向无环图模型,是一种概率图模型,一般由有向无环图和一个条件概率表组成,其中,节点表示随机变量
,有向线段表示变量之间有因果关系,并由此产生条件概率值 [17] 。
如图1是一个简单的贝叶斯网络。
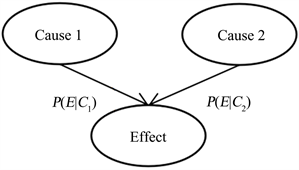
Figure 1. Simple Bayesian network diagram
图1. 简单贝叶斯网络图
图中包含三个随机变量Cause 1,Cause 2和Effect,很明显,节点Effect的取值或结果直接取决于Cause 1和Cause 2,由此,在三个变量节点间会产生条件概率表,由
和
组成。
2.2. 贝叶斯网络分类原理
2.2.1. 贝叶斯相关理论
在了解贝叶斯网络分类原理之前,我们需要先了解一些贝叶斯相关理论。
条件概率公式:
(1)
其中,
是后验概率,即事件B发生的前提下,事件A发生的概率;
是事件A发生的前提下,事件B发生的概率;P(A)是先验概率,即事件A发生的概率;P(B)是事件B发生的概率,P(B)不改变分类结果,是一个规范化因子,作用是获取后验概率的和等于1。
贝叶斯公式:
(2)
其中,
是后验概率,即事件B发生的前提下,事件
发生的概率;
是先验概率,即事件
发生的概率,且对于所有的事件
,有
成立;
是条件概率。
对于一组离散随机变量
,它们的取值分别为
的联合概率为
(3)
而贝叶斯网络中,在给定了父节点的条件下,每个节点
都与其非后代节点条件独立,由于这一变量节点的局部独立性,上式可以化简为
(4)
式中
,取值通常是已知的,其含义是结点
的父结点的集合。
2.2.2. 贝叶斯网络分类步骤
1) 设随机变量
,其取值分别为
,这里的每个
都是随机变量X的一个特征属性,可以是离散数据,也可以是连续数据,又或者同时包含离散变量和连续变量。
2) 假定有m个类别Y,记为
。
3) 所要得到的结果,就是给定一个未知分类的数据样本X,在已知X的数据的情况下,预测该待分类项所须归属的类别,也就是,利用
来决定其所属类别,其中,
(5)
3. 决策树模型
决策树又被称为判定树,是一种用于分类与回归的树形结构,一般可以认为是if-then规则的集合。决策树由结点和有向边组成,而结点则由内部结点和叶结点组成,其中,内部结点表示一种特征或者属性,而叶结点则表示一种类 [18] 。
3.1. 平均信息(熵)
信息:
(6)
平均信息(熵):
(7)
一般来说,熵越大,事件的发生越无序;熵越小,事件的发生越确定。
3.2. 树的建立/划分规则
本质上来说,决策树的建立其实就是在寻找一种能够使得熵能够在最大程度熵变小的划分方案。
一般来说,分为四个步骤:
1) 找到可以令平均熵最小的特征维度对数据集进行分割。
2) 对分割后的数据集再找寻可以使平均熵最小的特征维度,再对数据集进行分割。
3) 重复上面步骤直到用完所有特征、或者子集中目标标签全部相同。
4) 如果所有特征都用完,最终的子集中,目标标签仍不一致,则使用最多标签作为最终输出。
4. 仿真实验
4.1. 数据处理
本文利用贝叶斯网络模型和决策树模型对梅雨季节降水量进行研究,选取南京市2011年~2022年每年6月1日~7月31日的南京市机场58,238站逐日自动观测数据。
为了研究下雨天气背景下暴雨的气象观测要素的特征,文章选取地面以上2米处的当天最高温度(℃) (简称为最高温度),地面以上2米处的当天最低温度(℃) (简称为最低温度),气象站水平的大气压(mmHg) (简称为大气压),地面高度2米处的相对湿度(%) (简称为相对湿度),观测前10分钟内地面高度10~12米处的平均风速(m/s) (简称为平均风速)等观测要素。以降水量的多少作为分类类别,分为无降水天气与降水天气,其中,降水天气又分为普通降水天气(包括小雨,中雨,大雨,降水量为0.1~49.9 mm)和暴雨天气(包括暴雨,大暴雨,特大暴雨,降水量在50 mm以上)。
实验中,选取南京市2011~2021年6~7月的气象数据作为训练数据,2022年6~7月的气象数据作为测试数据。
4.2. 降水气象特征分析
本文以南京市2011~2021年每年6~7月的气象数据为研究背景,对南京市梅雨季节的降水以及降水量的多少的规律以及诊断模型进行分析。针对南京市梅雨季节降水天气的时间分布特征进行统计,对影响南京市6~7月降水天气的气象要素特征进行统计分析,也即研究南京市的降水天气的发生规律。
通过统计分析发现,如图2所示,降水天气累计发生频次268次,在每年的6月1日~7月31日均有发生,其中6月16日~7月15日发生频次较高,其余时间发生频次较低,发生频次最高时间段是7月1日~7月5日,累计发生了34次降水天气,占总降水频次的12.69%。未发生过特大暴雨。如图3所示,暴雨天气发生频次较为均匀,几乎每个时间段都有暴雨天气发生,且总频次也较低,只有15次,占全部降水天气的5.60%。
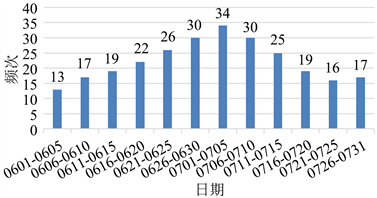
Figure 2. Time distribution diagram of rainy weather frequency
图2. 降水天气频次的时间分布图

Figure 3. Time distribution diagram of rainstorm weather frequency
图3. 暴雨天气频次的时间分布图
降水天气和暴雨天气发生时的大气压分布特征如图4与图5所示,降水天气的大气压在738.7 mmHg~756.3 mmHg区间内均有分布,主要分布在748 mmHg~752 mmHg这一区间,发生了160个时次,占比59.7%。暴雨天气发生的大气压区间分布在740.5 mmHg~755.2 mmHg,发生时次同样在748 mmHg~752 mmHg区间最为集中,占比53.3%。

Figure 4. Graph of atmospheric pressure frequency in rainy weather
图4. 降水天气的大气压频率图

Figure 5. Graph of atmospheric pressure frequency in rainstorm weather
图5. 暴雨天气的大气压频率图
降水天气和暴雨天气发生时的相对湿度分布特征如图6与图7所示,降水天气在相对湿度62%以上均有分布,主要分布在90%以上,发生了198频次,占比73.9%。暴雨天气发生的相对湿度区间分布在92%以上。

Figure 6. Graph of relative humidity frequency in rainy weather
图6. 降水天气的相对湿度频率图

Figure 7. Graph of relative humidity frequency in rainstorm weather
图7. 暴雨天气的相对湿度频率图
降水天气和暴雨天气发生时的平均风速分布特征如图8与图9所示,降水天气发生时,平均风速从0 m/s~10 m/s均有分布,平均风速在1~4时发生降水天气的时次占比89.6%,其中平均风速为2 m/s时发生降水天气的时次最多,有83次,占比31%。从图9可以看出,平均风速在2 m/s~3 m/s区间时,暴雨天气发生时次集中,且在平均风速为2 m/s时发生时次最多。
通过对降水天气和暴雨天气发生的气象特征要素进行统计分析,发现在发生降水天气时,是否会增强至暴雨天气需要具备以下几个条件才会更加有利:大气压在748 mmHg~752 mmHg区间内最为有利;相对湿度需在92%以上;平均风速在2 m/s~3 m/s之间。

Figure 8. Graph of mean wind speed frequency in rainy weather
图8. 降水天气的平均风速频率图
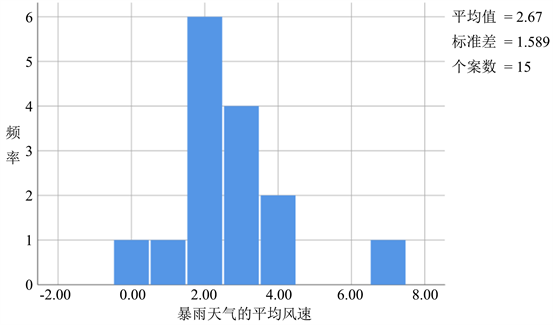
Figure 9. Graph of mean wind speed frequency in rainstorm weather
图9. 暴雨天气的平均风速频率图
4.3. 实验结果与分析
通过上述分析,可以得到降水天气和暴雨天气发生的一些有利条件,但现实中,各种天气发生的条件与可能性是一个十分复杂的非线性过程,尤其虽然南京市2011年~2021年6~7月间发生降水天气较多,但发生暴雨天气的频次并不算很高,具有较大的偶然性,想通过简单的定性条件就直接判定是否会发生暴雨天气是否发生并不容易。因此,本文会利用贝叶斯网络模型和决策树模型,对南京市的降水天气,尤其是暴雨天气是否发生建立诊断模型。
以是否为暴雨天气为模型的目标向量,模型的输入变量为最高温度,最低温度,大气压,相对湿度和平均风速。将预处理好的训练集和测试集数据输入模型,得到最终的结果。
建立一个贝叶斯网络,以是否降水为子节点,最高温度,最低温度,大气压,相对湿度和平均风速为父节点,得到的贝叶斯网络如图10。
将训练数据代入程序中,训练贝叶斯网络模型和决策树模型,然后进行测试数据的实验,将南京市2022年6月1日~7月31日的降水数据与所得结果对比,最终发现,贝叶斯网络模型的准确率为83.61%,而决策树模型的准确率为81.97%。
贝叶斯网络模型与统计相结合,相较于其他的如朴素贝叶斯模型、决策树模型等模型,贝叶斯网络模型有着独特的优势。贝叶斯网络模型结合图论知识,利用图模型描述各个变量之间的关系,更清晰易懂,也便于理解;不像朴素贝叶斯模型那样需要所有的特征变量都保持完全独立,贝叶斯网络模型对特征变量间的独立关系要求没有那么严格,也更符合实际;贝叶斯网络模型包含了因果关系和概率性语义,可以用于学习数据间的因果关系;贝叶斯网络模型最大的优势是可以处理不完备的数据集,因为它反映的是数据间的概率关系模型,所以可以有一定的数据缺失。
5. 总结
本文针对南京市每年6~7月期间梅雨季节的降水状况以及暴雨天气进行了时间特征和天气要素特征的分析,并利用贝叶斯网络模型和决策树模型对南京市58,238站点降水天气背景下的暴雨天气特征建立了诊断模型,得到以下结论:
1) 通过对南京市降水天气与暴雨天气特征的统计分析,发现暴雨天气的发生相较于普通降水天气的发生有着更为苛刻的气象条件的要求。
2) 基于贝叶斯网络模型分类算法对预处理数建立的诊断模型准确率为83.61%。
3) 基于决策树模型分类算法得到的决策树模型,可以看出,决策树的根节点是相对湿度,说明判断普通降水背景下的暴雨天气是否发生的最重要因素是相对湿度;决策树模型的准确率为81.97%。
4) 贝叶斯网络模型比决策树模型的准确率要稍微好一些,相较而言,贝叶斯网络模型计算更为方便,准确率也要稍高。
随着信息时代的发展,利用计算机对天气数据进行预测已经并且正在走向更为宽广的未来。将图论知识与人工智能等技术进行结合与优化,也将成为未来的一个发展趋势。
NOTES
*通讯作者。