面向大型家电零售的全渠道订单履约问题

Omni-Channel Order Fulfillment for Large Household Appliance Retail

摘要: 随着零售商布局全渠道的兴起，结合线上、线下渠道优化订单履约方案受到日益关注。大型家电零售存在着从订单接收到包裹发货的决策空窗期，本文研究的问题是利用该决策空窗期把订单分配给各渠道履约，以降低总的履约成本。考虑到库存水平的有限，采用订单拆分与库存转运策略。进一步根据订单的3种拆分方式(产品单分配、产品多分配、订单不拆分)分别建立混合整数规划模型，以对比不同拆分方式对总履约成本的影响。考虑到如今多数零售商采用的是即时履约策略，即接收到订单后立即履约，进一步设计了贪婪算法对即时履约进行模拟并与上述3种数学模型做比较。数值实验表明：产品多分配模型的成本最低，但与产品单分配差距极小；与订单不拆分模型和贪婪算法相比，采用订单拆分策略与库存转运策略能有效降低总的订单履约成本。

Abstract: With the rise of omni-channel retail, optimizing order fulfillment solutions by combining online and offline channels has become increasingly important. This article focuses on the decision window between receiving orders and shipping products in large home appliance retail, and studies how to allocate orders to different channels during this time to reduce overall fulfillment costs. Considering the limited inventory levels, the article proposes an order splitting and inventory transshipment strategy. Three different ways of order splitting (Product Single Allocation, Product Multiple Allocation, and Order Single Allocation) are established as mixed integer programming models to compare their impacts on total fulfillment costs. Given that most retailers nowadays adopt the just-in-time fulfillment strategy, which involves fulfilling orders immediately upon receiving them, this article further designed a greedy algorithm to simulate the just-in-time fulfillment process and compared it with the aforementioned three mathematical models. The numerical experiments show that the Product Multiple Allocation Model has the lowest cost, but the difference from the Product Single Allocation Model is minimal. Compared with the Order Single Allocation Model and the greedy algorithm, using the order splitting and inventory transshipment strategy can effectively reduce the overall order fulfillment costs.

1. 引言

在新零售兴起的时代，采用全渠道零售已成为一种流行的策略。全渠道零售指企业采取尽可能多的零售渠道类型进行组合和整合，以满足消费者购物、娱乐和社交需求。这些渠道类型不仅包括有形店铺和无形店铺，还包括信息媒体等等 [1] 。优衣库最先提出了“线上下单，门店提货”的零售策略。而小米在2020疫情期间推出了门店Go服务，用户可在微信小程序上选择附近的门店下单，并在营业时间安排配送和取货。这一策略极大缩短了订单履约所需的响应时间，类似于京东的前置仓同城配送。根据中国电子信息产业发展研究院发布的《2022年中国家电市场报告》，2022年我国家电市场规模达到8352亿元，同比下降了5.2%；但线上市场规模同比增长了4.24%，线上渠道占比进一步提升至58.2% [2] 。这表明对于传统线下家电零售商而言，开设线上渠道、整合渠道资源变得日益重要。

通常情况下，线上零售商对接收到的订单可以采用延迟履约和即时履约这两种方式进行处理。订单延迟履约，即对接收到的订单进行周期性检查并统一分配，可以利用这一个周期内零售商具有的资源达到最优的履约方案；即时履约是指把订单立即分配给仓库，属于短视的策略，因为它无法考虑零售商后续接收到的订单以及库存补充计划 [3] 。目前，有关订单分配的研究大多采用延迟履约策略。Xu等 [4] 在Xu, Allgor和Graves [3] 的基础上进一步研究在多个时间段内分配订单给履约中心的订单履约问题。Leung等 [5] 提出了和订单延迟履约类似的“仓库延迟策略”，该文章从理论和实践上将传统的供应链延迟策略扩展为线上零售背景的仓库延迟策略，通过将待处理的物流订单进行分组处理，从而解决物流过程的延迟问题。

然而，对于全渠道零售商而言，面临着在订单到达后，将订单分配给哪个渠道来履约的权衡问题。Alptekinoğlu和Tange [6] 在包含仓库与门店的两级配送网络中，探讨面对新增线上需求时，该把线上订单分配给门店还是更高一级的仓库来履约的权衡决策。Mahar等 [7] 则开发和评估了一种准动态分配策略，用于将未完成的线上订单分配给门店或履约中心履约。Ardjmand等 [8] 则在全渠道环境下联合决策订单分配问题和装箱问题。该研究考虑了两个履约渠道，一个是从履约中心(Fulfilment Centers, FCs)的现有库存中履约订单，另一个是当FCs无法满足订单需求时，将订单外包给批发商来履约。吴限和陈淮莉 [9] 研究了订单代发策略，即电子零售商直接将客户的订单交给供应商履约，供应商从零售商的商品利润中抽取部分作为代发奖励。

在订单分配时，由于库存水平不足，或者出于降低履约成本的考虑，线上零售商会采用将订单拆分成多个子订单由不同仓库履约的策略。根据现实情况，存在两种订单拆分方式：一种是基于产品种类进行拆分的“产品单分配”，即订单中每种产品只能分配给同一个仓库履约，每个子订单都包含不同的产品；另一种是基于数量拆分的“产品多分配”，子订单中可以包含重复的产品。然而，已有文献中同时采用两种拆分方式并进行对比的研究较少。Xu等 [3] 在订单分配中采用了基于数量拆分订单的方式。该研究假设一个顾客点只有一个包含不同种类产品的订单，且允许从不同仓库往顾客点发送货物，以满足订单总需求，是一个多商品网络流问题。同样基于数量拆分订单的研究还有Xu等 [4] 。而基于产品种类拆分的研究则大多集中在订单分配与车辆配送的联合决策，如张源凯等 [10] 、辛禹辰等 [11] 和孟湲易等 [12] 。通常，订单发生拆分的原因有两种：一种是拆分后可以降低履约总成本(如运输成本、订单拣选和打包成本)；另一种是库存水平不足，为了避免订单流失而进行拆分。然而，在现有文献中，较少有综合考虑运输成本、库存水平以及订单拣选和打包成本进行订单拆分决策的研究。Xu等 [3] 、Xu等 [4] 以及张源凯等 [10] 只考虑了运输成本；辛禹辰等 [11] 和孟湲易等 [12] 考虑了运输成本和库存水平，但未考虑订单拣选和打包成本。这表明在订单拆分原因的考虑上还有待更全面深入的研究。

当现有库存无法满足已知订单需求时，线上零售商通常还会采用被动转运的方式在同级仓库将进行库存转移。Torabi等 [13] 研究了基于被动转运的单一渠道订单分配问题。该研究假设可以在所有同级履约中心之间进行被动转运，并且不考虑转运提前期。基于Torabi等人的研究 [13] ，Naderi等 [14] 进一步考虑了门店之间的连接问题。只有当两个门店之间存在连接时，才允许在它们之间进行转运，且每个门店连接其他门店的数量有限。

综上所述，目前对于全渠道订单履约中的订单分配问题的研究还比较缺乏。在订单分配的研究方面，对订单拆分方式进行对比分析的文献较少，同时将订单拆分策略与库存转运策略进行结合的研究也存在空白。因此，本文旨在研究如何结合订单拆分与库存转运策略的全渠道订单分配问题，从而最小化总的订单履约成本。具体地，为了探究产品单分配、产品多分配以及订单不拆分这3种订单拆分方式对履约成本的影响，本文建立了对应的数学模型。此外，为了论述延迟履约相对即时履约的优越性，本文设计了贪婪算法对即时履约策略进行模拟，并以此为基准方法与3个数学模型进行对比。最后，通过案例分析验证了采用订单拆分与库存转运策略的有效性。

2. 问题描述

某大型家电品牌商为了寻求营收的新增长点，在全国各大城市开设了众多集产品体验、销售以及售后服务于一体的线下门店。在2020年疫情期间，为了使居民能够更加便利地购买产品，该品牌商推出了从线下门店送货到家的服务。至2021年隔离措施已经解除，但该品牌商仍保留了从门店发货的渠道。若某个地区的线上订单需求庞大，则品牌商会在该地区内建立数个履约中心，专用于履约该地区内的线上订单。此外，该家电品牌商的供应链网络中还设有服务于周边地区的区域仓库，用于线下门店与履约中心的补货，同时也承担履约线上订单的职能。对于该家电品牌商，其拥有三个履约线上订单的渠道(门店、履约中心、区域仓库），具有将大量订单进行统一分配以降低履约成本的规模优势。故研究全渠道下的订单分配是具有经济效益的迫切问题。

2.1. 全渠道零售配送网络

参照上述家电品牌商的供应链网络，建立了一个包含区域仓库W、履约中心F、线下门店S这三类供应点的全渠道零售配送网络，如图1所示。区域仓库W是服务于周边地区的中心仓库，一般位于郊区，负责从供应商进货并给履约中心和门店进行补货，同时也能履约线上订单。履约中心F是只履约线上订单的平台，一般位于近郊区。门店S既能线下销售又能履约线上订单，一般位于商业区。对于线上订单，该网络包含3种发货方式，即从区域仓库发货(Ship From Warehouse, SW)、从门店发货(Ship From Store, SS)以及从履约中心发货(Ship From Fulfillment Center, SF)。此外，为应对现有库存无法满足需求的情况，允许门店和履约中心这两类同级供应点进行紧急库存转运。

因为本文研究的订单分配问题属于短期的运营决策，所以在决策模型中把区域仓库的库存水平、能履约的订单数量都视作无限，并且不考虑区域仓库给门店和履约中心补货。由于库存容量有限，门店只保存了部分种类的产品，其线上线下库存共享。对于特大型家电等不方便在门店内存储的产品，只在区域仓库和履约中心有库存。受场地与人员的限制，履约中心和门店的产品库存水平、履约线上订单的数量有限，并且门店在这两项上均比履约中心小。此外，由于门店可以进行线下销售，顾客的到店购买会影响订单分配时的实际库存水平。根据以上的描述，可以对3类供应点的特征进行归纳，由表1所示。

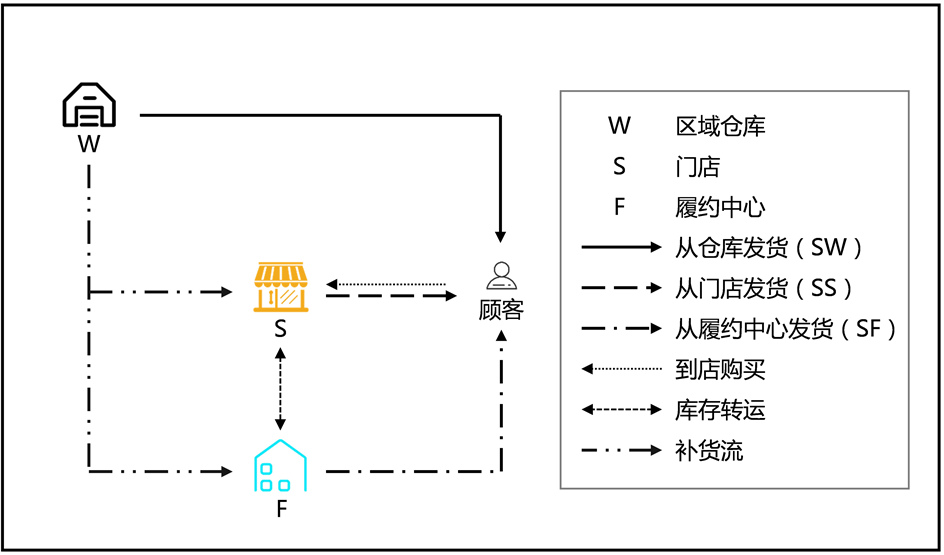
Figure 1. Omni-channel retail distribution network

图1. 全渠道零售配送网络

Table 1. Relevant characteristics of different supply points

表1. 不同供应点的相关特征

由于大型家电零售在下单到履约之间会有一个时间差，因此可以采用延迟履约策略，即在营业一段时间后对积攒的订单进行统一分配。综上，本文要解决的问题是在考虑库存转运的配送网络中，如何把一段时间内接收到的线上订单分配给各个供应点使得总履约成本最小。

2.2. 订单履约策略

1) 订单拆分

若每个订单都只分配给一个供应点履约，考虑到门店和履约中心库存水平的限制，可能会有较多订单被分配给距离更远的区域仓库履约，导致总体履约成本较高。出于降低总体履约成本的目的，允许线上订单进行拆分，即一个订单可以拆分成多个子订单。根据经验判断，子订单数量过多会导致顾客满意度降低，故本文设定每个订单最多拆分成2个子订单。根据现实情况，本文考虑订单拆分的方式有两种(图2)。一种是基于产品种类拆分的“产品单分配”，即订单内的一种产品只能由一个供应点履约，子订单包含的产品集互斥。另一种为基于产品数量拆分的“产品多分配”，即订单内的一种产品可以由多个供应点履约，子订单包含的产品集可以有交集。

Figure 2. Two ways of order splitting

图2. 两种订单拆分方式

Figure 3. Inventory transshipment

图3. 库存转运

2) 库存转运

当履约中心F和门店S的库存无法满足订单需求时，除了把订单分配给其他供应点，还可以在F、S这两类同级供应点间进行紧急库存转运以满足订单需求，降低总履约成本。接下来用一个例子描述该策略。如图3所示，有一个上海的订单包含2个香水和2个沐浴露，然而上海的履约中心F1、门店S2的库存水平都无法满足该订单需求。若不进行库存转运，则订单会被分配给位于杭州的履约中心F3。但在将上海F1的1个香水转运给上海S2后，就可以将订单分配给上海S2。

2.3. 订单履约策略

订单履约成本由产品在供应点的拣选与打包成本、订单送达客户的运输成本以及库存转运成本构成。假设零售商将订单配送与库存转运外包给第三方公司进行，考虑的订单运输成本由固定运输成本和可变运输成本构成。固定运输成本表示供应点在启动该订单的运输时需支付的启动费用，不同类型的供应点其固定运输成本不同。可变运输成本则表示支付固定运输成本后的附加费用，该附加费用与产品重量和运输距离成正比。对于库存转运成本，由于库存转运可以一次性转运大量产品，故只考虑线性的转运成本，与产品重量和运输距离成正比。

3. 产品单分配模型

产品单分配模型(Product Single Allocation Model, PSA)，即考虑订单中的产品只分配给一个供应点。在建立模型之前，需阐述重要的建模假设以及各个符号的含义。

3.1. 建模假设

根据前文描述的问题特点，对产品单分配数学模型提出如下重要假设：

1) 所有的订单都可以履约，不发生缺货(顾客在下单时可以查看产品剩余库存，若库存不足则无法下单)；

2) 供应点的服务范围有限，只有订单所属的顾客片区在供应点的送货半径内时，才能将订单分配给该供应点；

3) 由于库存容量限制，门店只保存了部分种类的产品；

4) 为了平衡库存，门店S和履约中心F可以发生库存转运；且对于大型家电等无法在门店仓库内存储的产品，不允许从履约中心往门店转运；

5) 订单可以拆分为2个子订单，且订单内的一种产品只能由一个供应点履约；

6) 暂不考虑门店线下销售。

3.2. 符号说明

1) 集合：

J——供应点集合， $j\in J$ ， $J=W\cup F\cup S$ ；

W——区域仓库集合， $j\in W$ ；

F——履约中心集合， $j\in F$ ；

S——门店集合， $j\in S$ ；

K——顾客片区集合， $k\in K$ ；

$J_k$ ——可送货至顾客片区k的供应点集合， $j\in J_k$ ， $\forall k\in K$ 。 $J_k=\left\{j\in J|d_{jk}\le r_j\right\}$ ， $d_{jk}$ 表示从供应点j到顾客片区k的距离， $r_j$ 表示供应点j的送货半径；

I——订单集， $i\in I$ ；

$I_k$ ——属于顾客片区k的订单集， $i\in I_k$ ， $\forall k\in K$ ；

P——产品集， $p\in P$ ；

$P_s$ ——能存储在门店仓库内的产品集， $p\in P_s$ ， $P_s\subset P$ ；

$P_i$ ——订单i包含的产品组成的集合， $p\in P_i$ ， $\forall i\in I$ ；

2) 参数：

$b_j$ ——履约中心或门店j履约订单的数量上限， $\forall j\in F\cup S$ ；

$I_{pj}$ ——履约中心或门店j中，产品p的库存水平， $\forall j\in F\cup S,p\in P$ ；

$d_{jk}$ ——从供应点j到顾客片区k的距离(km)， $\forall j\in J,k\in K$ ；

$d_{j{j}^{\prime }}$ ——从供应点j到供应点j'的距离(km)， $\forall j\in J,j^{\prime }\in J,j^{\prime }\ne j$ ；

$n_{pi}$ ——订单i中产品p的数量， $\forall i\in I,p\in P$ ；

$w_p$ ——产品p的重量(kg)， $\forall p\in P$ ；

$c_{pj}^1$ ——产品p在供应点j的拣选与打包成本(￥/unit)， $\forall j\in J,p\in P$ ；

$c_j^2$ ——订单由供应点j发货的固定运输成本(￥/order)， $\forall j\in J$ ；

$c^3$ ——单位可变运输成本(￥/(kg∙km))；

$c^4$ ——单位转运成本(￥/(kg∙km))；

3) 决策变量：

$z_{ij}$ ——订单分配决策变量，0-1变量，1表示订单i由供应点j履约， $\forall i\in I,j\in J$ ；

$x_{pij}$ ——产品分配决策变量，0-1变量，1表示订单i中产品p由供应点j履约， $\forall p\in P,i\in I,j\in J$ ；

$q_{pj{j}^{\prime }}$ ——转运决策变量，连续变量，表示从供应点j往供应点j'转运产品p的数量， $\forall j,j^{\prime }\in F\cup S,j^{\prime }\ne j,p\in P$ ；

3.3. 数学模型

目标函数(1)是最小化总的订单履约成本。第一项表示订单内的产品在供应点的拣选与打包成本。第二项表示订单i由供应点j履约的固定运输成本。第三项表示订单i中产品p由供应点j履约时，从供应点j发往顾客片区k的可变运输成本。最后一项表示库存转运成本。

式(2)为订单分配约束，表示订单至少由1个供应点履约(不发生订单拆分)，至多由2个供应点履约(最多拆分为2个子订单)。式(3)表示当所选供应点与顾客片区的距离超出供应点送货范围时，供应点不能履约该顾客片区的订单。式(4)表示履约中心与门店履约的订单数量不得超过其上限。式(5)为履约中心与门店的库存水平约束，保证了在履约中心和门店履约的产品数量不会超过其经过库存转运后的库存水平。式(6)为转运规则约束，表示不允许将不属于门店仓库内的产品从履约中心转运到门店。

式(7)为单分配约束，保证了订单内的一种产品只能由一个供应点履约(但一个供应点可以履约同一订单内的多种产品)。式(8)和(9)为决策变量 $x_{pij}$ 和 $z_{ij}$ 的逻辑关系约束。式(8)保证了只有订单i中产品p的数量 $n_{pi}$ 大于等于1且订单i被分配给供应点j履约时， $x_{pij}$ 才可以为1。式(9)确保了在 ${\displaystyle {\sum }_{p\in P}{x}_{pij}}=0$ 的情况下 $z_{ij}$ 为0；且 $z_{ij}=1$ 时， ${\displaystyle {\sum }_{p\in P}{x}_{pij}}$ 至少为1，即每个子订单至少包含一件产品。式(10)至(12)为决策变量取值范围。

4. 模型对比

为了对比不同订单拆分策略相较于订单不拆分的效益，以及订单拆分策略与库存转运策略的相互作用，本章将建立产品多分配模型(Product Multiple Allocation Model, PMA)以及订单不拆分模型(Order Single Allocation Model, OSA)，并分别与PSA进行比较。这两个模型与产品单分配模型(PMA)在建模逻辑上的差异为：送货上门的订单是否进行拆分，若拆分以何种方式。由此导致决策变量的设定不同，并在目标函数与约束方程上也存在部分差异。

4.1. 产品多分配模型

产品多分配指订单发生拆分时一种产品可以由多个供应点履约。故产品多分配模型(PMA)的建模假设需由假设(5)改为“订单可以拆分为2个子订单，且订单内的一种产品最多可以由2个供应点履约。”该模型的产品分配决策变量为连续型变量 $y_{pij}$ ，表示订单i中产品p由供应点j履约的数量， $\forall p\in P,i\in I,j\in J$ 。其余符号表示与PSA相同，PMA表达如下：

目标函数(13)同样是最小化总的订单履约成本，其各项的含义都与目标函数(1)一致，但由于决策变量的差异，在第一项和第三项里用 $y_{pij}$ 替代了(1)的 $n_{pi}\cdot x_{pij}$ ，表示订单i中产品p由供应点j履约的数量。

式(14)也是库存水平约束，其含义亦与式(5)相同，但同样用 $y_{pij}$ 替代了(5)的 $n_{pi}\cdot x_{pij}$ 。式(15)是需求约束，表示从各个供应点 $j\in J$ 履约产品p的数量总和必须满足订单i所要求的数量 $n_{pi}$ 。

式(16)和(17)为决策变量 $y_{pij}$ 和 $z_{ij}$ 的逻辑关系约束。式(16)保证了只有订单i被分配给供应点j履约时， $y_{pij}$ 才可以大于0，其中 $n_{pi}$ 为 $y_{pij}$ 的上界。式(17)确保了在 ${\displaystyle {\sum }_{p\in P}{y}_{pij}}=0$ 的情况下 $z_{ij}$ 为0。式(18)为 $y_{pij}$ 取值范围。

4.2. 订单不拆分模型

订单不拆分指一个订单只能由一个供应点履约。故订单不拆分模型(OSA)的建模假设需由假设(5)改为“订单不可以拆分。”除了决策变量中不包含 $x_{pij}$ 以外，其余符号表示与产品单分配模型一致。综上，OSA表达如下：

OSA与PSA相比，除了不含决策变量 $x_{pij}$ ，还有如下差异：

1) 目标函数(19)的第一项和第三项都是在目标函数(1)的基础上用 $z_{ij}$ 替代 $x_{pij}$ ，分别表示订单不可拆分时的拣选与打包成本和可变运输成本；

2) 相比式(2)，式(20)表示每个订单只能分配给1个供应点履约；

3) 式(21)不等式的左项是在式(5)的基础上用 $z_{ij}$ 替代 $x_{pij}$ ， ${\displaystyle {\sum }_{i\in I}{n}_{pi}\cdot z_{ij}}$ 表明当订单不可拆分时，若订单i由供应点j履约，则i所需产品p全部由j满足；

4) 不含产品单分配式(7)；

5) 不含逻辑式(8)至(9)。

5. 模型对比

为了考察不同履约策略对订单分配结果的影响，本章将通过数值实验对前文提及的三个模型(PSA, PMA, OSA)在履约成本、订单拆分数、库存转运次数、三个渠道分配到的订单数等指标上进行对比。本节还设计了订单到达后立即履约的贪婪算法，用于模拟现实中零售商大多采用的即时履约策略。以贪婪算法作为基准对比三个数学模型的效用。在最后一部分则对模型进行灵敏度分析，进一步剖析库存水平、库存转运策略、子订单拆分数量限制对成本的影响。数学模型的求解采用CPLEX 12.9，贪婪算法用C++实现，运行环境为64位Intel i7-4720HQ 2.60 GHz CPU和16 GB RAM的计算机。

5.1. 算例构建

算例采用的部分地理位置数据来自上海市浦东新区的物流网点：门店S来自小米之家的线下门店，顾客片区K来自菜鸟驿站网点。履约中心F与区域仓库W的位置则为人工设置。从上述数据集中随机抽样构成一张位于浦东新区的全渠道零售配送网络(图4)，其包含：1个区域仓库，3个履约中心，10个门店以及40个顾客片区。因此测试算例中 $\left|W\right|=1$ ， $\left|F\right|=3$ ， $\left|S\right|=10$ ， $\left|K\right|=40$ 。通过计算各个网点的欧氏距离获得供应点j到顾客片区k的距离 $d_{jk}$ ，以及供应点j到供应点 $j^{\prime }\ne j$ 的距离 $d_{j{j}^{\prime }}$ 。其余参数设置如下：

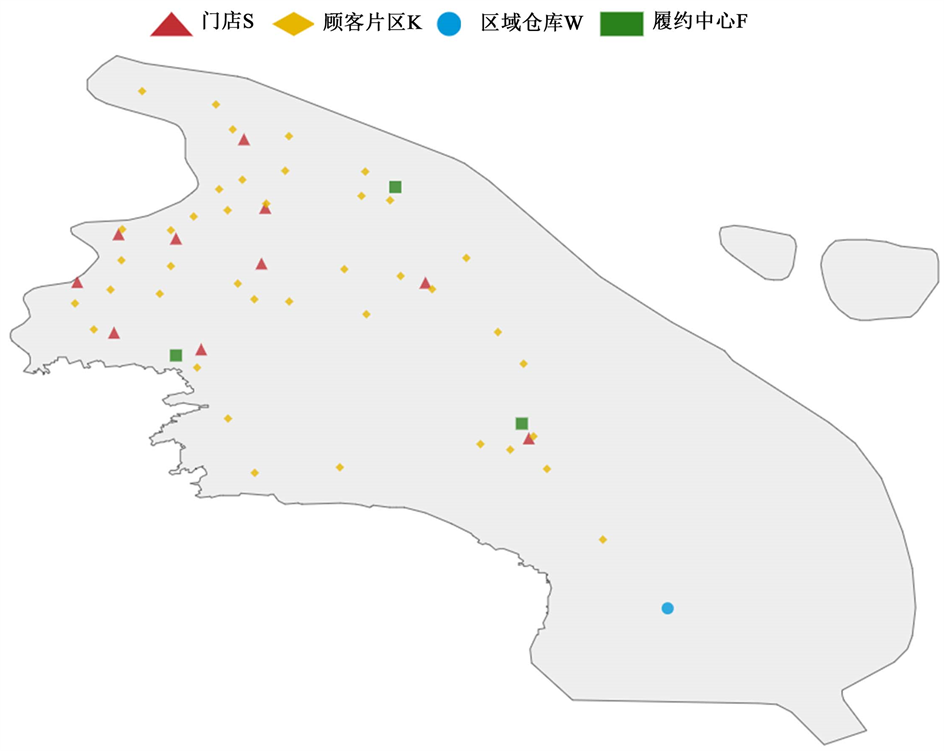
Figure 4. Omni-channel retail distribution network located in Pudong New Area

图4. 位于浦东新区的全渠道零售配送网络

1) 对于区域仓库 $j\in W$ ，送货半径 $r_j=1000\text{km}$ ，表示能服务所有顾客片区。对于履约中心 $j\in F$ ， $b_j=200$ ， $r_j=30\text{km}$ 。对于门店 $j\in S$ ， $b_j$ 是由均匀分布 $U_d\left[60,80\right]$ 随机生成的整数， $r_j=30\text{km}$ ；

2) 产品种类 $\left|P\right|=100$ ，其中能存储在门店仓库内的产品 $\left|P_s\right|=60$ 。对于 $p\in P_s$ ，产品重量 $w_p$ 服从 $U_d\left[5,15\right]$ ；对于 $p\in \left(P\backslash P_s\right)$ ， $w_p$ 服从 $U_d\left[15,50\right]$ ；

3) 设置订单数 $\left|I\right|=1000$ 。顾客片区k的订单集 $I_k$ 包含订单数量 $\left|I_k\right|=\alpha \cdot \left|I\right|/\left|K\right|$ ， $\alpha$ 是由均匀分布 $U_d\left[0.5,1.5\right]$ 确定的实数。为了模拟订单的生成，将 $U_d\left[1,6\right]$ 种产品随机分配给每个订单。每个产品被分配到的概率相同，且被选中产品的需求数量 $n_{pi}$ 满足平均值 $\mu$ 为1，标准差 $\sigma$ 为 $U_d\left[0.7,1.2\right]$ 的正态分布；

4) 设所有订单对产品p的总需求 $n_p={\displaystyle {\sum }_{i\in I}{n}_{pi}}$ 。对于 $j\in F$ ， $p\in P$ ， $I_{pj}=\beta \cdot n_p/\left|F\right|$ 。对于 $j\in S$ ：若 $p\in \left(P\backslash P_s\right)$ ， $I_{pj}=0$ ；若 $p\in P_s$ ， $I_{pj}=\beta \cdot n_p/\left|S\right|$ 。 $\beta$ 是由 $U_d\left[0.8,1.2\right]$ 随机生成的实数；

5) 成本参数的设置参考了Arslan [15] 等的研究，如表2所示。

Table 2. Cost parameter table

表2. 成本参数表

5.2. 对比的基准方法

在前文第2章与第3章中，提出了3个基于“延迟履约策略”的数学模型，其中PMA、OSA作为PSA的基准模型，用于分析不同订单拆分策略的效果以及相较订单不拆分时的成本节约比值。进一步的，为了评估“延迟履约策略”相较“即时履约策略”的效用，在本节设计了贪婪算法用于模拟零售商接收到订单后立即履约的场景。由图5，贪婪算法的流程如下。首先赋予订单集合I随机的订单到达顺序，零售商根据到达顺序依次履约订单。对于每个订单，首先找到离订单i所在顾客片区k最近的供应点j，若j的库存能满足订单的至少一种产品，则把订单i分配给供应点j；接着检查订单i是否仍有产品的需求未满足，若有则寻找下一个最近的供应点j，把剩余种类的产品全部分配给该供应点。在贪婪算法中，采用的订单拆分方式为产品单分配，且每个订单最多拆分为2个子订单。在分配订单i到供应点j时，还需保证 $j\in J_k$ ，并且分配到j的订单数不超过 $b_j$ 。由于每次运行贪婪算法其订单到达顺序都不相同，为了更好地模拟现实中订单的到达情况，在进行实验时将对同个算例运行3次贪婪算法并对求解结果取平均值。

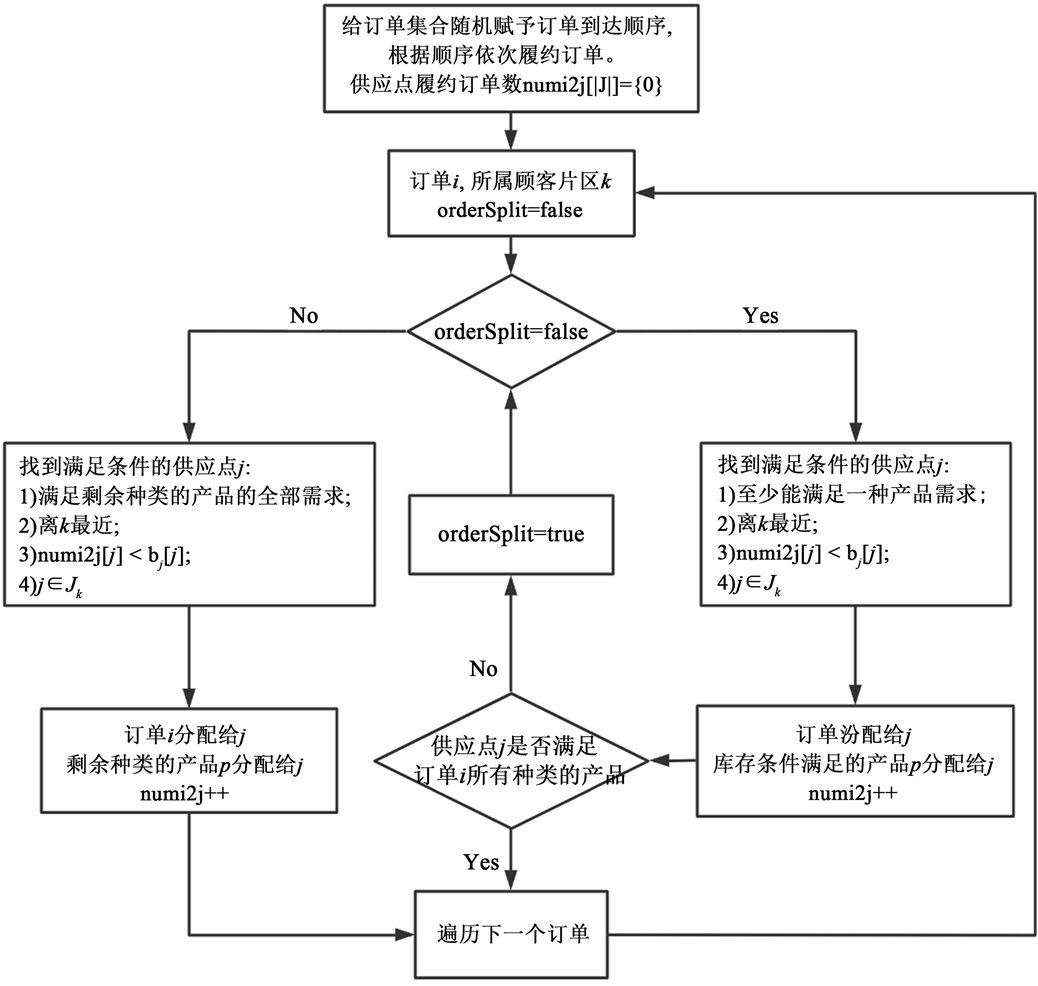
Figure 5. Flowchart of greedy algorithm

图5. 贪婪算法流程图

5.3. 实验结果

1) 三个模型与贪婪算法的对比

对随机生成的算例分别运用3个模型以及贪婪算法进行求解，得到的实验结果如表3所示。其中，“履约总成本” = “拣选与打包成本” + “固定运输成本” + “可变运输成本” + “转运成本”。由表3可知，PMA的履约总成本最低，但与PSA差距极小，二者在其余各项数据上也几乎一致。从经验上分析，产品多分配的总成本之所以比单分配低，在于其考虑的决策场景更细致，允许订单中的同种产品被分配给多个供应点。“产品多分配次数”的计算方式为：遍历所有订单，若订单中的某个产品被分配给2个供应点履约，则加一。该项平均值为8，仅有极少的订单会发生产品多分配，这解释了PMA相较PSA在成本降低方面并不显著的原因：即便PMA的决策场景更细致，但大多数订单采用产品单分配的效果即可逼近PMA。

与OSA相比，前两个模型的履约总成本都有不小的节约比率，分别为11.530%与11.533%，说明了采用订单拆分策略的有效性。比较三个模型的成本组成，由于固定运输成本 ${\displaystyle {\sum }_{j\in J}{\displaystyle {\sum }_{i\in I}{c}_j^2\cdot z_{ij}}}$ 与订单数成正比，即便订单不拆分可以获得更小的固定运输成本，但总体上订单拆分的收益要高于不拆分。

“订单拆分数”表示有多少订单进行了拆分。PSA与PMA的订单拆分数相近，订单拆分率(订单拆分数/|I|)都接近38%。即便限制了一个订单最多只能拆分为2个子订单，仍有相当多数量的订单进行了拆分。与贪婪算法相比，PSA、PMA与OSA有极大的成本节约比率，分别为37.5%、37.5%以及29.3%。分析贪婪算法的成本组成，发现与前三个模型的主要差距在于可变运输成本，相较三个模型依次增长了45%、44.9%以及34.6%。在订单拆分数量上，贪婪算法相对PSA与PMA分别增长了29.5%与30%。说明无论是从成本或订单拆分数量角度考虑，采用数学规划的三个模型，总能得出比贪婪算法更好的结果。

“库存转运次数”表示是否在供应点j与j'存在转运流，若 ${\displaystyle {\sum }_{p\in P}{q}_{pj{j}^{\prime }}}>0$ 则转运次数加一。最多有 $A_{\left|F\right|+\left|S\right|}^2=156$ 条转运流，则“库存转运占比” = 库存转运次数/156。“产品转运总数”表示一共转运了多少单位的产品。“承接转运的供应点满足需求总数”即对所有接收了产品转运的供应点，其一共履约了多少件产品。则“供应点需求由转运满足占比” = 产品转运总数/承接转运的供应点满足需求总数。通过对比可以发现：相较OSA，PSA、PMA“库存转运次数”与“产品转运总数”更大，靠产品转运来满足需求的占比也更高。说明联合运用订单拆分策略可以使库存转运策略发挥更大作用。

Table 3. Solution result

表3. 求解结果

2) 三个履约渠道的对比

由于全渠道零售配送网络中有多个履约渠道，有必要分析在不同数学模型与贪婪算法下，三个履约渠道(W, F, S)在各项数据的分布情况，见表4。“订单分配数”表示有多少订单被分配给该渠道。相较OSA，PSA与PMA分配给门店S的订单数更多，说明运用订单拆分策略后，门店S发挥了更大的订单履约职能。而贪婪算法分配给门店S的订单最多，占比达44.2%。

“转出产品数”表示各渠道转运出的产品数量。“转入产品数”表示各渠道承接转运的产品数量。在PSA与PMA中，履约中心F转运出的产品占产品转运总数的76%以上，而门店S承接了97%以上的转运产品。而在OSA中，门店S转出产品数占69.8%，履约中心F则承接了67.4%的转运产品。由于决策时为非补货期，区域仓库W无法给履约中心F与门店S补货。上述数据说明：在联合运用订单拆分策略时，采用库存转运策略后，F相当程度上承担了给S补货的功能；而单独运用库存转运策略时，反而是S一定程度上给F补充了库存。

Table 4. Data distribution of each channel for three channels

表4. 三个渠道的各项数据分布

5.4. 灵敏度分析

灵敏度分析用于分析模型中系数的升降、变量以及约束的删减对目标函数的影响。首先对影响履约总成本最大的库存水平进行分析，通过对算例的初始库存水平进行放缩，来模拟现实中不同程度的库存水平下模型的表现。接着分析采用库存转运策略对降低履约总成本的贡献。最后则通过删除对应约束来阐述限制子订单拆分数量的必要性。

1) 库存水平

由于库存转运与订单拆分都是库存紧缺而采用的紧急应对策略，可以预见数值实验中库存水平的设置会影响履约总成本、订单拆分数以及产品转运总数等结果。为了考察不同库存水平的影响，对已有算例的库存水平乘上 $\alpha$ 倍，即新库存水平 ${I^{\prime }}_{pj}=\alpha \cdot I_{pj}$ 。分别取 $\alpha$ 等于0.5、0.75、1.25、1.5、1.75、10，得到各项指标(表5-1~5-3)并分析变化趋势。取 $\alpha$ 等于10是考虑库存极度充裕的情况。

由表3与表5-1、表5-3可知，随着 $\alpha$ 从10变换到0.5，除了倒数第二项数据，其他数据总体上都在递增。“订单拆分数”在 $\alpha$ 从10到1时处于波动状态，但随着 $\alpha$ 递减到0.5发生明显增长。而“库存转运次数”、“产品转运总数”以及“供应点需求由转运满足占比”则随着 $\alpha$ 递减而稳定递增。说明随着库存的紧缩，订单拆分策略与库存转运策略发挥了更大的作用，这是符合预期的结果。当 $\alpha =10$ 时，PSA与PMA的求解结果完全一致，PMA的产品多分配次数为0，PSA与PMA的产品转运次数皆为0。说明在库存极度充裕的情况下，库存转运策略已经失去效用，但订单拆分策略仍然有效。而即便在库存极度充裕的情况下，采用延迟履约策略(PSA, PMA, OSA)依旧比即时履约(贪婪算法)效果更好。

在求解时间上， $\alpha$ 从1.25递减到0.5时PSA与PMA都发生了明显的递增，且PMA递增幅度更大。但PSA与PMA的履约总成本差距始终很小，若在库存紧缺的情况下，采用PSA更能满足决策者对迅速得出决策方案的需求。

Table 5-1. Indicators after changes in inventory levels (1)

表5-1. 变化库存水平后各项指标 (1)

Table 5-2. Indicators after changes in inventory levels (2)

表5-2. 变化库存水平后各项指标 (2)

Table 5-3. Indicators after changes in inventory levels (3)

表5-3. 变化库存水平后各项指标(3)

Table 6. Cost comparison based on OSA and greedy algorithm

表6. 以OSA与贪婪算法为基准时的成本对比

通过对比不同 $\alpha$ 下的成本数据，绘制表6表示以OSA、贪婪算法为基准时，其他模型的履约总成本降低比率。可以发现PSA与PMA相对OSA的成本降低比率随着 $\alpha$ 的递增而增加，说明库存越充裕，采用订单拆分策略越有必要。PSA、PMA、OSA相对贪婪算法的成本降低比率可能存在一个阈值，当 $\alpha$ 为1时比率最大， $\alpha$ 小于或者大于1该比率都递减。但无论 $\alpha$ 取值多少，采用延迟履约策略(PSA, PMA, OSA)相比即时履约(贪婪算法)都能节约相当大的成本。

2) 不考虑库存转运，删除转运变量 $q_{pj{j}^{\prime }}$

为了对比采用库存转运策略相较不采用的效果，还需删除PSA、PMA、OSA模型中的 $q_{pj{j}^{\prime }}$ 并重新进行数值实验，实验结果见表7。对比表3发现，不采用库存转运策略时，PSA、PMA与OSA履约总成本分别增长了0.68%、0.61%以及0.62%，PSA、PMA的订单拆分数增加了8与17。上述结果说明采用库存转运策略具有降低成本、减少订单拆分数的现实意义。

Table 7. Results without using inventory transshipment strategy

表7. 不采用库存转运策略的结果

Table 8. Solution results without limiting the number of sub-order splits

表8. 不限制子订单拆分数量的求解结果

3) 不限制子订单拆分的数量

在PSA与PMA模型中，为了考虑现实因素，限制了一个订单最多拆分为2个子订单。若移除该约束会对结果产生什么样的影响，本文也进行了实验分析。同时，为了进行更全面的对比，也需对前文的贪婪算法的框架做出修改，使得一个订单可以被拆分为2个以上的子订单，见图6。此外，还同时考虑了不同初始库存水平的情况，设库存放大系数 $\alpha$ 为1与0.5。

实验结果如表8所示，与表3、表5-1对比发现：1) 无论是哪种初始库存水平，PSA、PMA履约总成本相对原模型变化极小；2) $\alpha =1$ 时，仅有1~2个订单被拆分成了2个以上子订单，而 $\alpha =0.5$ 时该数据骤增到21与23；3) 贪婪算法表现更差， $\alpha$ 为1与0.5时，履约总成本相对原模型分别增长了4.0%与1.6%，并且有相当数量的订单被拆分成2个以上子订单，说明限制子订单拆分个数反而使得贪婪算法有更好的表现。综上，在库存水平较低的条件下，可能会有较多订单被拆分成2个以上子订单，为了不降低顾客满意度，有必要设置子订单拆分数量约束。

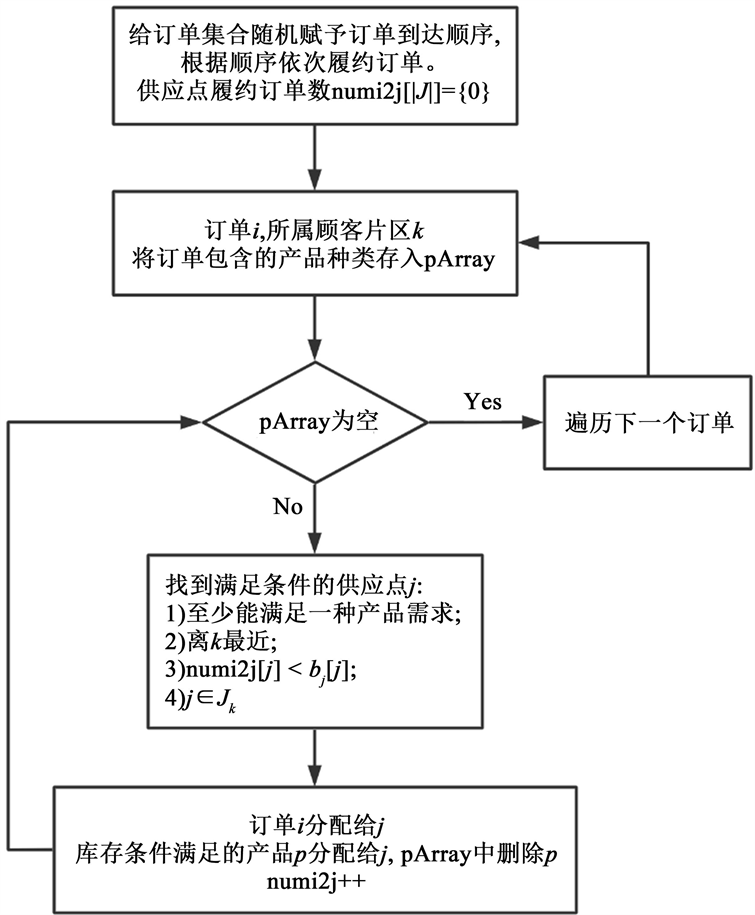
Figure 6. Flowchart of greedy algorithm without limiting the number of sub-order splits

图6. 贪婪算法流程图–不限制子订单数量

6. 结语

本文建立了大型家电零售的全渠道订单履约模型，其核心决策逻辑在于利用顾客在下单到把订单分配给供应点的决策空窗期，对一段时间内积攒的订单进行统一分配，即延迟履约策略。而创新之处就在于提出了订单拆分与库存转运相结合的订单分配模型。订单拆分与库存转运都是应对库存紧缺的紧急策略。由于订单拆分方式有产品单分配与多分配两种，为了对比两种拆分方式的效应，分别建立产品单分配模型(PSA)与订单不拆分模型(PMA)。为了对比PSA、PMA相对订单不拆分的效益，本文还建立了订单不拆分模型(OSA)。

在案例分析部分，则提出了模拟即时履约的贪婪算法，用于对比前面提到的3种数学模型。根据案例分析的结果，可以知道PSA与PMA的表现几乎一致，且相对OSA都有11.5%以上的成本降低比率。而与贪婪算法对比，3种数学模型更是有极大的成本降低比率，分别为37.5%、37.5%以及29.3%。从库存转运的角度分析，还得出了联合运用订单拆分策略可以使库存转运策略的效果更好的结论。

为了分析初始库存水平对履约成本以及订单拆分、库存转运策略的影响，本文还对初始库存水平进行灵敏度分析。通过分析订单拆分与库存转运相关的指标发现：1) 随着库存的紧缩，订单拆分策略与库存转运策略发挥了更大的作用；2) 在库存极度充裕的情况下，库存转运策略已经失去效用，但订单拆分策略仍然有效，且PSA、PMA、OSA相对贪婪算法依旧有更好的表现。通过对比PSA、PMA、OSA与贪婪算法的成本发现：1) 库存越充裕，采用订单拆分策略越有必要；2) PSA、PMA、OSA相对贪婪算法的成本降低比率可能存在一个阈值，当 $\alpha$ 为1时比率最大， $\alpha$ 小于或者大于1该比率都递减。最后验证采用库存转运策略以及限制一个订单最多拆分成2个子订单的必要性。

考虑到现实情况下，零售商在决策时门店仍能进行线下销售，影响决策时的可用库存，进一步研究将考虑线下销售对订单分配决策的影响。

NOTES

^*通讯作者。