1. 引言
信息技术的发展为教育行业带来了机遇与挑战,加强信息技术在教育领域的建设是新时代教育需迫切解决的问题。20世纪80年代,“可视化”一词的出现引起了大量学者的关注,信息技术的发展使得可视化成为可能,数学可视化成为教育领域的一个研究趋势。
数学是研究数量关系和空间形式的科学。《普通高中数学课程标准(2017年版2020年修订)》中指出:重视信息技术与数学课程内容的有机整合,加强学生对数学本质的认识 [1] 。我国虽已推行信息技术与数学课堂整合多年,但多停留在使用PPT、希沃白板等这样较为低层次的层面,部分教师会使用几何画板、超级画板等一些数学软件,但这些软件对于教师的操作能力要求较高,实施效果并不可观。GeoGebra软件是解决各类数学问题强有力的可视化工具,它操作简单、即学即用,能够帮助学习者洞悉数学本质,架起抽象的“数”与可见的“形”之间的桥梁,真正实现“教懂、教活、教深”。基于此,本研究将利用可视化技术,介绍GeoGebra环境下的一些数学可视化教学案例,帮助学生降低认知负荷,把握数学知识本质,实现深度学习。
2. GeoGebra
GeoGebra (简称GGB)是由Markus Hohenwarter于2001年所开发的一款免费开源的动态数学软件。GeoGebra一词是由Geometry (几何学)和Algebra (代数学)组合而成,体现几何与代数相结合的功能特点,是解决各类数学问题的强有力的可视化工具 [2] 。GGB是一款结合几何、代数、表格、三维、概率计算等多功能为一体的动态数学软件,通过对数学对象加以塑造,产生直观的视觉印象,提供对象的多重表征,揭示数学知识的生成过程,将抽象知识具体化。若能将该软件深度融合于数学课堂,学生便能闻其声、见其形、入其境,主动参与数学课堂,深刻把握数学本质。
GeoGebra、几何画板与超级画板是数学中常用的教学软件,能够弥补传统教学的不足,但三者在设计理念、功能偏好和操作界面等存在差异,如表1所示。


Table 1. Comparison of GeoGebra, geometry artboard and super artboard
表1. GeoGebra、几何画板与超级画板的比较
从上述表格中,不难发现:GeoGebra比几何画板和超级画板功能更强大、易操作。3D绘图功能、概率统计等功能更是其他软件所不具有的,是唯一一款开源免费软件。正因为如此,GeoGebra软件正逐渐取代几何画板,成为最适合数学教育教学的辅助软件。
3. GeoGebra环境下的可视化教学案例
高度的抽象性和严密的逻辑性是数学学科的特点。可视化教学可以使抽象内容变得形象直观,基于这一特点,本文将设计GeoGebra环境下的可视化教学案例,构建“所见即所得”的情境,实现“数”与“形”的联系表征,促进学生对数学学科深层次的理解和应用。
3.1. 创设历史情境,认识杨辉三角
在高中数学教科书中,有一个非常重要的定理——二项式定理,即
[3] 。杨辉三角是二项式
在
时展开
式所组成的一个数表,由中国古代数学家贾宪于公元11世纪发现,原名“开方作法本源图”。杨辉三角蕴含了丰富的数字规律和数学思想方法,具有数学对称美、简洁美、和谐美以及数形结合的统一美,以数学文化作为问题背景向学生介绍杨辉三角的发展史,让学生在数学探究中感受美,如图1和图2所示。
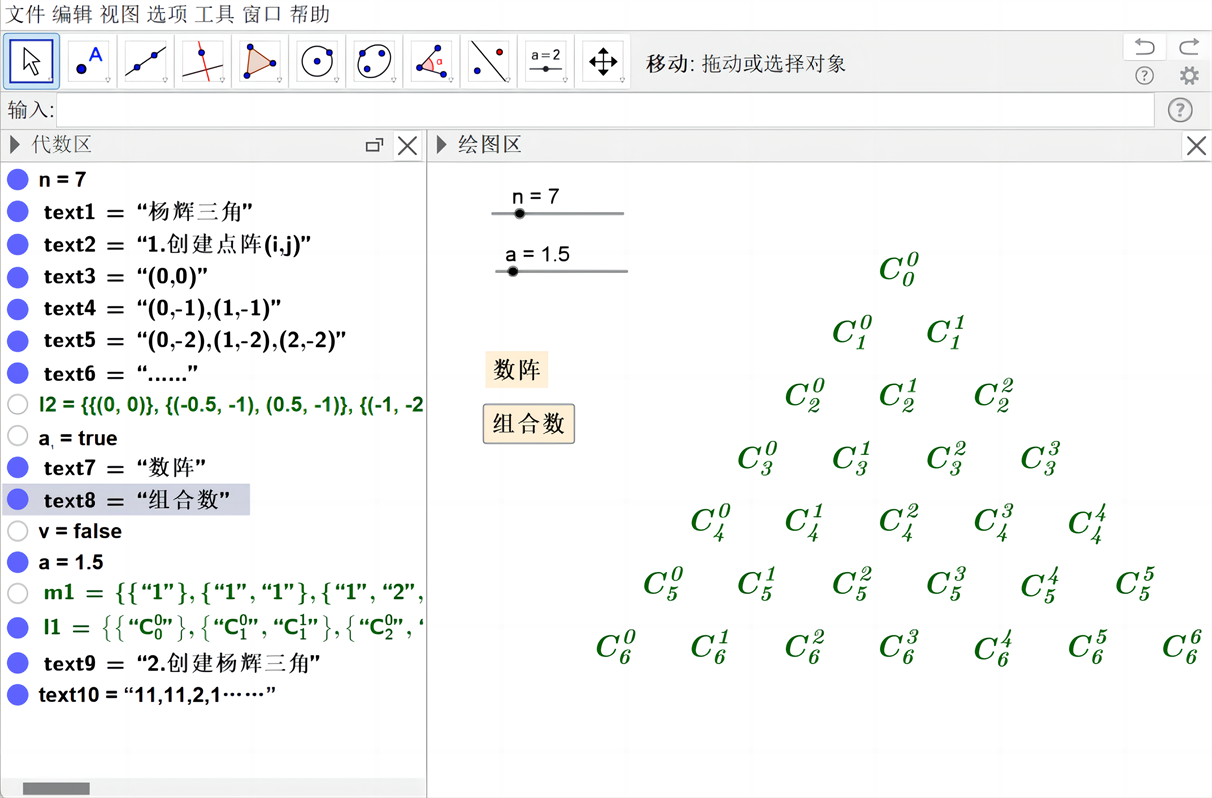
Figure 1. Yang Hui triangular number array
图1. 杨辉三角数阵
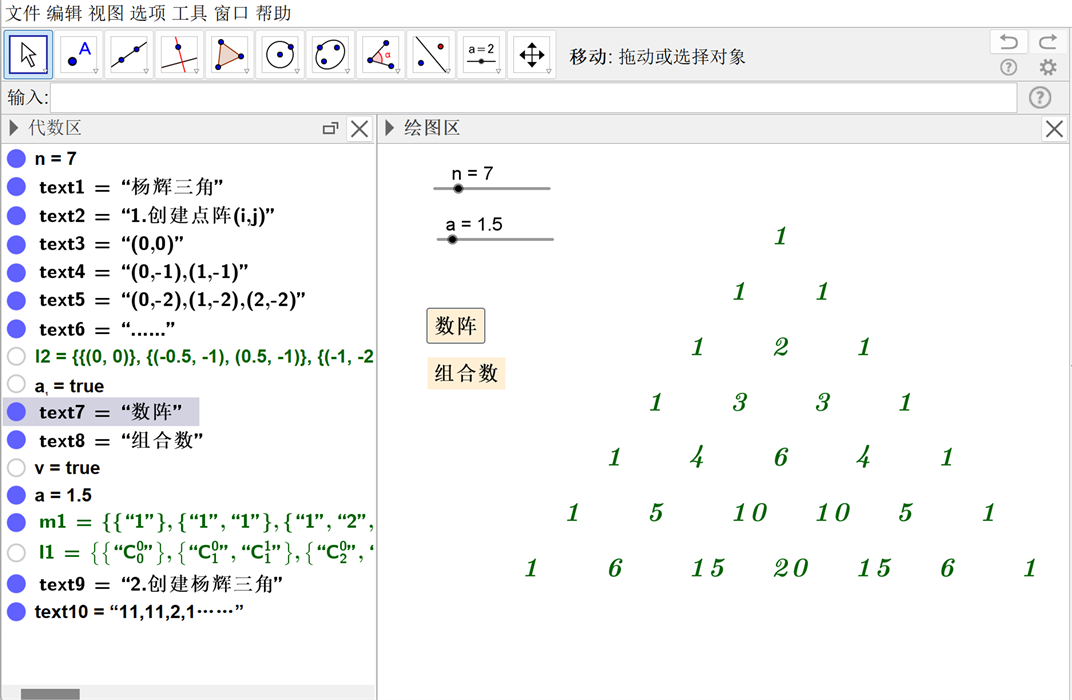
Figure 2. Yang Hui triangular combination number
图2. 杨辉三角组合数
当前新课程改革倡导将数学文化融于课堂教学,对学生进行数学文化的熏陶,采用多样化的教学方式实施教学。借助GeoGebra软件中的复选框控制数表的显示与隐藏,发挥滑动条的优势分析数表的特点,将该数表进行可视化呈现,探究杨辉三角中所蕴含的数学思想,让学生的思维浸润在数学文化中,感受杨辉三角的数学严谨之美、灵活之美。
3.2. 构造对象实体,描绘三角函数
三角函数是典型的周期函数,充分体现周期性这一函数性质的特点。在人教版高中数学教科书中,利用单位圆上点的坐标定义任意角的三角函数,利用圆几何性质的解析表述描述三角函数“周而复始”的性质。借助GeoGebra软件将三角函数可视化,其动态功能可将图象从不同角度展示给学生,有利于揭示单位圆与三角函数的联系,理解三角函数的本质特征与图象变换,渗透化归思想和数形结合思想。

Figure 3. Image of a unit circle and a sinusoidal function
图3. 单位圆与正弦函数图象
教师利用GeoGebra软件展示:将单位圆12等分可得到13个终边不同的圆心角,角的终边与单位圆上点的纵坐标就是其所对应的正弦值。以13个圆心角的大小为横坐标,以其终边与单位圆的交点的纵坐标为纵坐标,在平面直角坐标系中描点,如图3所示。借助GeoGebra软件可视化呈现单位圆上的点,利用复选框控制点的轨迹的显示与隐藏,发挥滑动条的优势,精确绘制正弦函数图象,突破难点,帮助学生认识到正弦函数概念的本质,体会其定义与图象之间的内在逻辑联系。
3.3. 展示探究过程,内化导数概念
导数是微积分的基本概念,反映了函数相对于自变量的变化速度,即变化率。瞬时变化率是一种无
限趋近的变化过程,学生经历探究活动过程归纳导数的概念:函数
在任一点
的瞬时变化率就是函数
在该点处的导数,记作
。
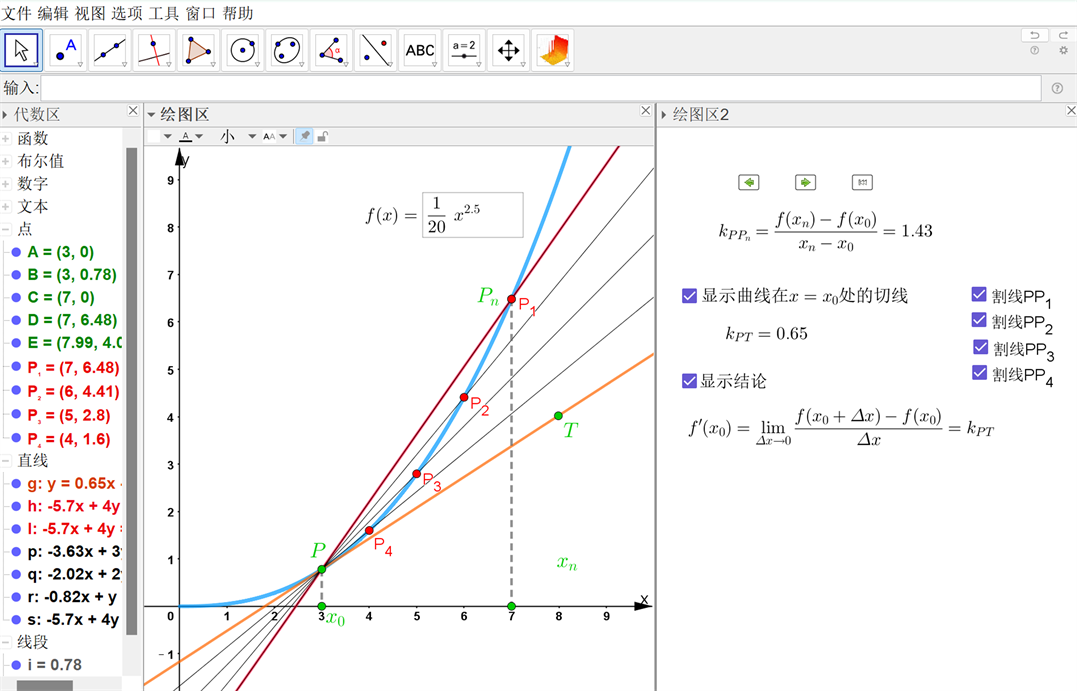
Figure 4. The geometric meaning of derivatives
图4. 导数的几何意义
导数作为解决函数单调性、极值、最值问题的一个重要工具,具有高度抽象性,因此许多学生未能深入理解导数概念的本质。若利用GeoGebra将导数概念的形成过程可视化,如图4所示,学生了解导数概念的生成过程,直观感知导数的几何意义,从“数”与“形”两个角度认识平均变化率与割线斜率之间的关系,体会极限的思想。通过文本框中输入函数的解析式,由特殊到一般,作出任意函数及其导函数的图象并以动态文本的形式加以呈现。学生经历对函数图象的操作、观察、比较、分析等一系列的探究过程,由外显的观察活动逐渐过渡到内隐的抽象分析过程,学会在图象的变化过程中寻找规律,对瞬时变化率有直观深刻的感受,加深对导数概念本质的认识,发展数学抽象素养和直观想象素养。
3.4. 创设动态情境,形成椭圆概念
历史上,古希腊人从圆柱或圆锥的截口上发现椭圆,阿波罗尼斯在《圆锥曲线》中采用截线定义椭圆,并总结出椭圆焦半径之和等于常数这一性质 [4] 。在人教版教科书中,“椭圆及其标准方程”一节先直接给出椭圆的画法,再给出椭圆的定义。通过调查发现,学生对此心存疑惑:为什么要这样定义椭圆呢?课本上的椭圆画法是如何产生的?这些疑惑实质上是教学中对椭圆概念形成过程忽略的体现。
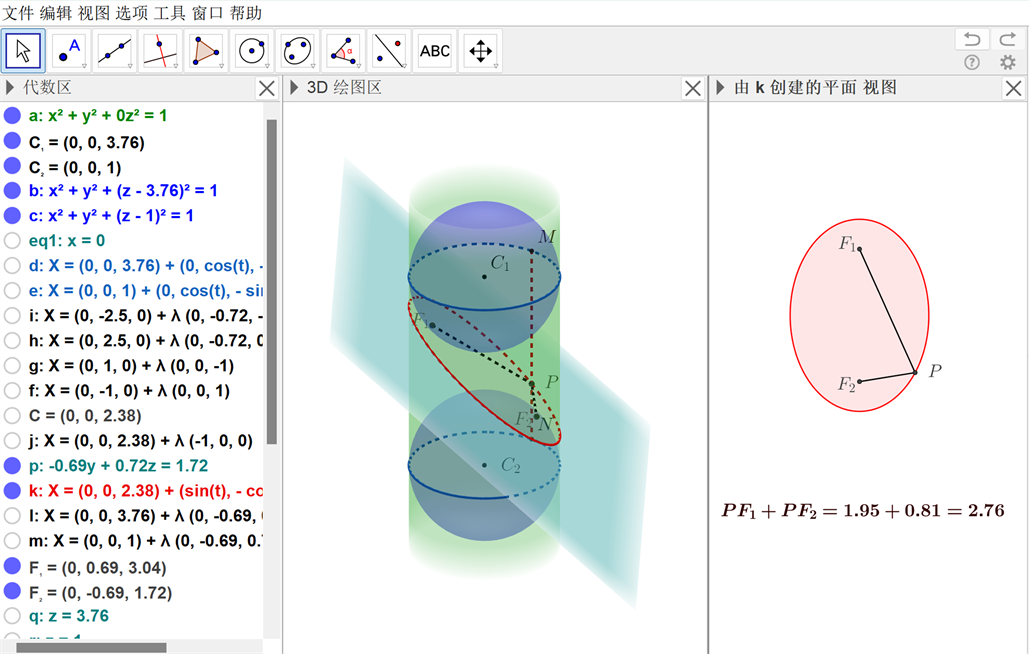
Figure 5. The cylinder of the Dandelin double-sphere model
图5. 旦德林双球模型之圆柱
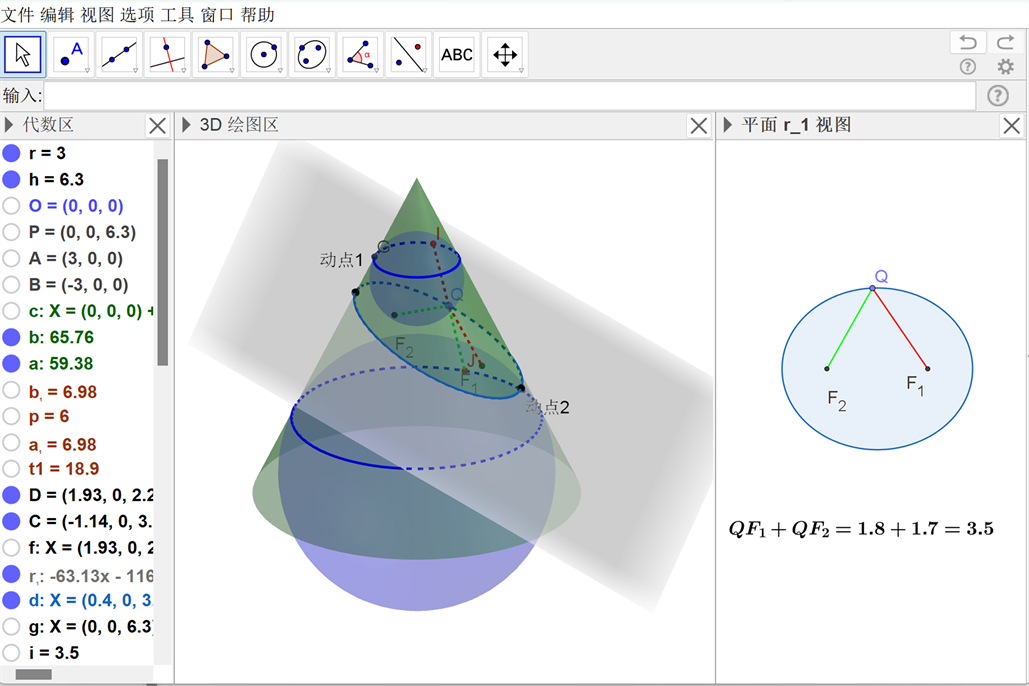
Figure 6. The cone of the Dandelin double-sphere model
图6. 旦德林双球模型之圆锥
普通高中数学课程标准中指出,教学要体现数学知识的发生发展过程,促进学生的自主探索。从具体事实出发,由生活中的椭圆入手,基于旦德林双球模型开展探究实验,重构椭圆概念的发生发展历史,学生经历从截面定义到书本定义的知识发展过程,理解椭圆概念产生的来龙去脉 [5] 。如图5和图6所示,借助GeoGebra软件可视化展现几何元素的运动过程,利用平面视图中度量工具证实“椭圆上的点到两定点的距离之和是定值”这一事实,实现模型实验与教材定义的有机统一,加深学生对椭圆概念的深度理解,达到深度学习的目的。
3.5. 注重知识联系,表征数列性质
数列是一种特殊的离散型函数,课程标准中提出要让学生体会等差数列与一元一次函数的关系。教师要有全局观,引导学生注重知识的连贯性,结合图象分析数列的性质,引导学生善于思考,勤于迁移。
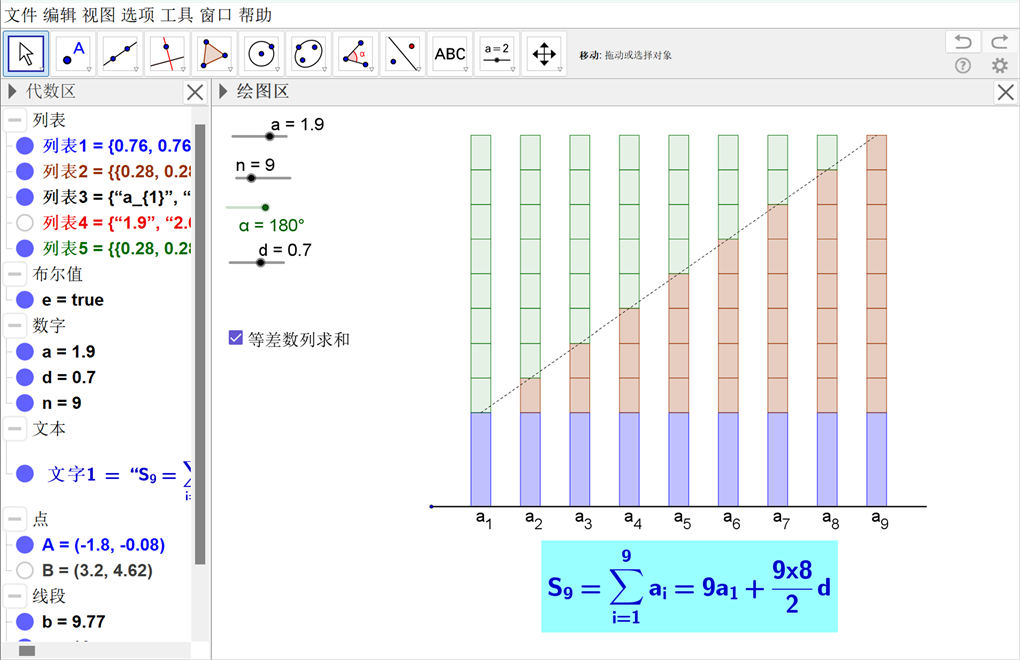
Figure 7. Image of the sum of the first n terms of an arithmetic series
图7. 等差数列前n项和的图象

Figure 8. A function representation of the sum of the first n terms of an arithmetic series
图8. 等差数列前n项和的函数表示
数列是由点列构成的特殊函数,具备函数的某些性质。等差数列的通项公式可以看作是an关于n的一次函数,等差数列的求和公式可以看作是Sn关于n的二次函数。在教学中,可以引导学生用函数的眼光看待数列,体会数形结合的重要思想。基于“数形结合”设计的可视化学习情境,不仅能促进学生对知识的理解,还能打造一些简单的可交互场景,激发学生学习兴趣,辅助知识建构 [6] 。如图7和图8所示,采用GeoGebra软件中的“序列”指令构造数列,利用“文本”指令完成数据显示,创建滑动条实现首项、公差、项数的改变,在动态演示中归纳总结数列的性质,将数列进行可视化表征,必然有助于学生深刻理解数列的知识,提升学生的思维层次,发展直观想象和数学运算素养。
3.6. 理清数理关系,揭示几何特征
立体几何是培养学生空间想象能力和空间观念的重要载体,其教学重点是帮助学生形成空间观念,发展直观想象素养。学生之所以学起来有困难,是因为平面几何知识的负迁移对学生的知识结构产生影响,加之教学工具的表达能力受限等,使得立体几何成为学生的“难题”。
在几何体的侧面展开图的教学过程中,若采用传统教学方式,教师直接在黑板上手工绘制图象,较为抽象。倘若采用GeoGebra软件中的3D绘图区与平面视图区结合展示,利用其动态功能将展开图从不同角度展示给学生,则有助于突破教学难点。例如,在圆柱体的展开图教学过程中,在GeoGebra环境下创建滑动条控制圆柱度底面半径和高度,如图9所示,输入一系列指令实现几何体的展开,通过拖动角度滑动条呈现圆柱的侧面展开过程,如图10所示,有助于帮助学生实现由立体几何向平面几何的过渡,降低认知难度。

Figure 10. The cylindrical side unfolding process
图10. 圆柱侧面展开过程
再如,利用参数法作图,展示圆锥、圆台的侧面展开过程,如图11和图12所示。学生可以借助图示分析几何关系,通过圆锥、圆台的侧面与切线之间角度变化制作其展开过程,拖动滑动条改变圆锥、圆台的大小,将圆锥、圆台沿着母线展开,使得立体图形平面化。教师利用GeoGebra揭开立体几何展开图的面纱,转隐性知识为显性知识,引导学生去领略化归思想方法的美丽容颜,渗透化归思想,揭示数学知识本质 [7] 。
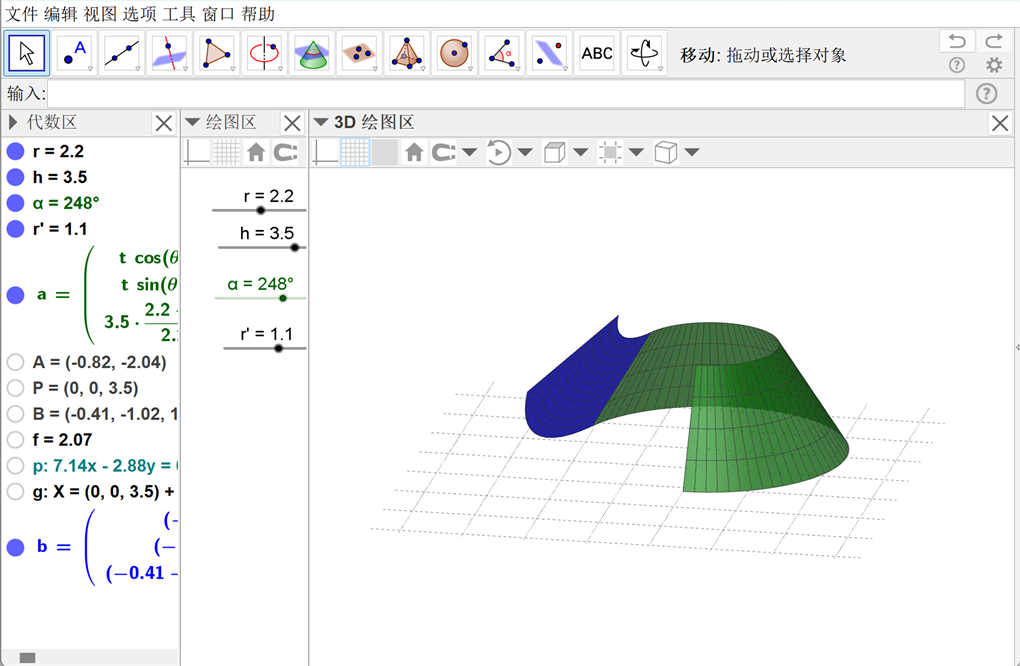
Figure 12. The roundtable side unfolding process
图12. 圆台侧面展开过程
4. GeoGebra深度融合于中学数学的教学策略
4.1. 情境创设,化被动为主动
高中教材中的现实情境所涉及到的数据在进行处理和运算时较为复杂,若仅依靠教师讲解不免晦涩,借助GeoGebra创设数学实验情境,引入与实际结合的模拟实验情境,吸引学生的兴趣和注意力。例如,在正态分布的教学过程中,创设高尔顿钉板数学实验情境,不仅可以调动学生学习的主动性和积极性,而且有利于发展学生的数学建模素养 [8] 。
4.2. 动态演示,化抽象为直观
在传统教学中,隐形轨迹只能依靠想象来完成,GeoGebra却可以追踪轨迹的动态生成,将隐形轨迹可视化,使其由“隐性”走向“显性”,化抽象为直观。这项技术充分显示了几何与代数之间的密切联系,体现了数形统一的辩证性,是高效的可视化教学策略。例如,在正弦函数的新授课中,借助单位圆构造正弦函数图象,采用实体工具则费时费力,而借助GeoGebra追踪轨迹技术则可以大大降低难度,化抽象为直观,揭示三角函数概念的本质,实现概念的深度学习,发展学生数学抽象与直观想象素养。
4.3. 数据分析,化复杂为简单
在统计板块中,经常遇到纷繁的数据需要进行处理、分析,借助GeoGebra软件对数据进行拟合、回归分析、绘图等操作,将复杂数据转化为可视化的图象与图表,化繁为简,大大降低教学难度,增强学生对数据的认识、分析和借助数据解决问题的能力,培养学生数据分析核心素养。
4.4. 数形结合,化静态为动态
GeoGebra教学软件突破传统课堂的限制,以其强大的功能优势,将抽象、静态的几何图形以直观、动态的形式呈现于学生眼前。例如,在球的体积公式的教学过程中,呈现球的体积公式的数学发展过程,借助祖暅原理“幂势既同,则积不容异”来推导球的体积公式 [9] 。拖动滑动条改变几何元素相关参数,让学生观察并总结变中不变的规律,数学课堂成为探究式的高效课堂,有利于培养学生的自主探究能力,发展学生逻辑推理素养和直观想象核心素养。
5. 展望
信息技术与数学课堂的融合实现了以学生为中心的学习模式,在这种模式中,教师扮演着组织者、引导者和合作者的角色。借助GeoGebra软件将可视化案例运用于教学实践,通过动态演示将抽象、静态的数学知识直观化、动态化,在此过程中,渗透数形结合的思想,加深学生对于数学知识本质的理解,有效拓展学生思维。但需要注意的是,技术仅仅起到辅助作用,实际教学中仍要根据学生的理解能力和学习程度进行优化和完善,使其更加高效地服务于课堂。
基金项目
国家自然科学基金项目(11501309);2023年江苏省研究生实践创新项目“单元教学促进高中数学深度学习的实践研究”(SJCX23_1773)。