钛酸钡晶体中氧空位对光学性质的影响

Effect of Oxygen Vacancy on Optical Properties in Barium Titanate Crystals

摘要: 本文基于密度泛函理论，研究了在BaTiO₃晶体中不同电荷态(0, +1, +2)氧空位的缺陷形成能。采用杂化密度泛函修正了DFT-GGA带边问题。使用FNV方法对缺陷形成能量进行修正。给出了包含电子–声子耦合的F中心和F+中心的光谱的比较准确描述。结果表明：氧空位是浅施主能级，是该材料n型导电的主要原因。根据本文的计算结果，F心吸收峰位于2.85 eV (435 nm)，F+心吸收峰则位于2.80 eV (443 nm)。F心的发射峰位于2.83 eV (438 nm)，F+心的发射峰位于2.78 eV (446 nm)。计算结果与实验结果基本一致。结果表明，这些方法对点缺陷光谱的计算是可行的。该方法的主要优点是计算量比较低，远远低于多体微扰理论GW方法中的计算量。本文的方法在满足计算精度的条件下，解决了计算量巨大的问题。为研究点缺陷的光谱性质提供了有效途径。

Abstract: In this paper, based on density functional theory, the defect formation energies of oxygen vacancies with different charge states (0, +1, +2) in BaTiO₃ crystals were investigated. Hybrid density functional is used to solve the edge of the band problem of DFT-GGA. A finite size correction scheme (FNV) was used to correct the defect formation energy. An accurate description of the spectra of F and F+ centers involving electron-phonon coupling is given. The results show that the oxygen vacancy is a shallow donor level, which is the reason for the n-type conductivity of the material. According to our calculation results, the F core absorption peak is located at 2.85 eV (435 nm), and the F+ core absorption peak is located at 2.80 eV (443 nm). The emission peak of the F center is 2.83 eV (438 nm), and that of the F+ center is 2.78 eV (446 nm). The results are consistent with the experimental results. The results show that these methods are feasible for the calculation of point defect spectra. The main advantage of this method is that the computational cost is much lower than the GW method of multi-body perturbation theory. The method in this paper solves the problem of the huge amount of computation under the condition of satisfying the calculation accuracy. It provides an effective way to study the spectral properties of defects.

1. 引言

BaTiO₃ (BTO)作为典型的铁电材料，由于其优异的电学性能：铁电性、高介电常数、压电性和热释电性，被广泛应用于电容器、储能器件、传感器和执行器等领域 [1] - [8] 。它具有立方钙钛矿结构，这是研究最多的结构 [9] 。尽管该材料的应用范围很广，但纯BTO陶瓷的介电常数随温度变化很大，限制了其实际应用。

BTO陶瓷因其高介电常数，成为最早在多层陶瓷电容器研究中应用的材料。受主掺杂BTO晶体会引起V_O (氧空位)的迁移，氧空位的迁移会引起材料的绝缘电阻大幅下降，从而影响其性能。为避免和抑制材料中氧空位的迁移，20世纪90年代后，人们开始采用向材料中掺杂施主和受主离子来抑制氧空位的迁移，现在更多地是采用掺杂稀土元素的方法，如Y³⁺、Dy³⁺、Ho³⁺ [10] [11] 。氧空位的存在对材料性质及其稳定性有明显的影响。因此，不仅需要从科学的角度，而且需要从技术的角度对这种缺陷状态进行详细的研究。

本文将利用密度泛函理论对缺陷的性质进行了研究。密度泛函理论低估了带隙，因此，本文采用更精确的杂化密度泛函来修正带隙。本文还采用先进的修正方法修正带电缺陷的缺陷形成能。修正后的形成能是获得比较准确的缺陷转化能级的条件，在此基础上考虑电子与声子的耦合作用，计算获得光谱线形。

2. 计算模型和方法

立方晶系的BTO晶体空间群为Pm3m。本文计算晶体缺陷采用的超晶胞则是在原胞的基础上扩大3 × 3 × 3得到的135个原子的超晶胞结构，其中包括27个钛原子、27个钡原子、81个氧原子，超晶胞结构如图1所示。氧空位的缺陷模型即在超晶胞中挖掉一个氧原子。为了计算方便，BTO晶体中的氧空位是由移除四个钡原子和两个钛原子共用的一个氧原子而产生的，分数坐标为(0.50000, 0.50000, 0.66667)。

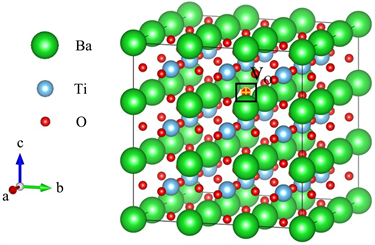
Figure 1. Diagram of oxygen vacancies (the position marked V_O in the diagram is the position of the oxygen atom to be deleted)

图1. 氧空位示意图(图中标记V_O的位置即为需要挖掉的氧原子的位置)

本文中采用了LDA + U的方法计算BTO晶体的电子结构与光学性质，一般来说，对于强关联体系以及含有d和f轨道价电子的原子需采用Hubbard U模型，我们使用U = 3.2 eV、J = 0.9 eV [12] 模拟钛离子的3 d轨道的库仑相互作用。

本文的原胞及超晶胞计算是基于从头算模拟软件包(VASP)，基于密度泛函理论(DFT)，采用缀加平面波方法(PAW) [13] 描述电子相互作用，并采用广义梯度近似(GGA)中的Perdew-Becke-Ernzerh (PBE) [14] [15] 处理交换相关能。钙、钛、钡和氧的价电子分别为：Ti：3d²4s²，Ba：5p⁶6s²，O：2s²2p⁴。针对BTO晶体的计算时，平面波的截断能设置为510 eV。K点利用Monkhorst-Pack [16] 取样方法在布里渊区采用5 × 5 × 5 K点网格进行结构优化和静态计算。电子自洽迭代的收敛精度为10⁻⁷ eV/atom。计算中使用的这些参数都是经过严格的收敛性测试(收敛标准是能量差小于1 × 10⁻³ eV)。

3. 计算结果和讨论

3.1. 缺陷形成能修正

本文主要是在对氧空位的三种不同价态(0, +1, +2)分别进行结构优化的基础上进行静态计算，并计算其对应的缺陷形成能以及缺陷转化能级。电荷态为q的缺陷D的缺陷形成能的表达式为 [17] ：

$E^f\left(D^q\right)=E\left(D^q\right)-E\left(perfect\right)+{\Sigma }_i{n}_i{\mu }_i+q\left({\epsilon }_{VBM}+{\epsilon }_F-\Delta V_{0/b}\right)-E_{corr}$ (1)

上式中， $E\left(D^q\right)$ 表示含价态q缺陷的超胞的总能， $E\left(perfect\right)$ 表示完整晶体的总能。 $n_i$ 表示i原子的原子数量，i即为原子种类，在本部分i指的是氧原子。当从超胞中移除原子时， $n_i>0$ ，反之，在超胞中额外加入原子时， $n_i<0$ 。 ${\mu }_i$ 是对应缺陷元素的化学势，此处， ${\mu }_i$ 指的是一个氧原子的化学势。 ${\mu }_{\text{O}}=\frac{1}{2}E\left({\text{O}}_2\right)=-4.93\text{eV}$ 。 ${\epsilon }_{VBM}$ 是完整晶体价带顶(VBM)的能量， ${\epsilon }_F$ 指的是完整晶体的费米能级， $\Delta V_{0/b}$ 表示完整BTO晶体与含缺陷晶体之间的平均静电势之差，最后一项 $E_{corr}$ 则是缺陷修正项。

在计算带电缺陷晶体时，由于周期性边界条件，带电缺陷与其镜像之间的库仑作用带来的误差不能忽略，所以为了消除带电缺陷之间的静电相互作用，将采用Freysoldt、Neugebauer、Van De Walle [18] [19] (FNV)修正方法来修正缺陷形成能以得到更为准确的计算结果。

本文采用FNV修正方法去修正带电缺陷之间的库仑相互作用。经修正后，计算得到不同价态稳定结构下带不同电荷缺陷的形成能见表1。表1的结果是在富氧条件下，费米能级设置在价带顶的情况下计算得到。

Table 1. Oxygen vacancy defect formation energy (eV) (Fermi level set at valence band top (VBM), oxygen rich condition)

表1. 氧空位缺陷形成能(eV) (费米能级设置在价带顶(VBM)、富氧条件)

3.2. 带边修正

广义梯度近似(GGA)和局域密度近似(LDA)方法计算材料的结构较为准确，但其有一个很大的问题就是在计算半导体以及绝缘体材料的能带结构时会严重低估材料的禁带宽度，与实验值之间相差甚多。由于带边的不准确，带来的一个很严重的后果就是计算时无法准确确定缺陷转化能级的位置。为了解决这个问题，本文将在这一部分用杂化泛函HSE来修正材料的能带结构。

本文给出的采用GGA-PBE和HSE方法计算的完整BTO晶体的能带结构都是基于其对应原胞模型结构，通过两种计算方法得到的结果显示：BTO晶体都是间接带隙。杂化泛函HSE [20] [21] 可以描述为

$E_{xc}^{hybrid}=\alpha E_x^{Fock}+\left(1-\alpha \right)E_x^{GGA}+E_c^{GGA}$ (2)

如图2所示，本文可以选择一个公共参考能级Φ (common reference level) (钛酸钡晶体的平均静电势)。图中的红色实线表示缺陷转化能级所处的位置， ${\mu }^{\text{semilocal}}$ 表示缺陷转化能级到GGA-PBE计算的价带顶的能量， ${\bar{\mu }}^{\text{semilocal}}$ 表示缺陷转化能级到公共参考能级Φ的能量。在HSE能带中， ${\mu }^{\text{hybrid}}$ 表示缺陷转化能级到HSE计算的价带顶的能量， ${\bar{\mu }}^{\text{hybrid}}$ 则表示缺陷转化能级到公共参考能级Φ的能量。由以上分析可以知道，缺陷转化能级到公共参考能级Φ的能量是相同的，但相对于价带顶的位置不同。所以，在带边修正之后得到缺陷转化能级的位置。首先我们需要求得带边修正的值，即HSE和GGA-PBE方法计算得到的价带顶的能量差。

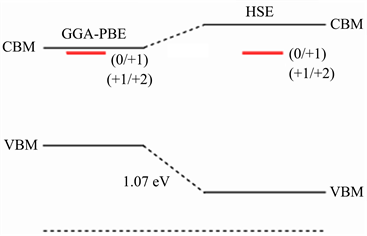
Figure 2. The position of the oxygen vacancy defect transformation level in the band gap (red line) (GGA-PBE and HSE correspond to the band gap calculated by the two methods, respectively)

图2. 氧空位缺陷转化能级在禁带中的位置(红线) (GGA-PBE和HSE分别对应两种方法计算得到的禁带宽度)

$\Delta E_{VBM}=E_{VBM}\left(PBE\right)-E_{VBM}\left(HSE\right)$ (3)

在得到 $\Delta E_{VBM}$ 之后，可以通过缺陷转化能级公式求得该转化能级位置 [22] ：

$\epsilon \left(q/q^{\prime }\right)=\frac{E^f{\left(D^q\right)}_{{\epsilon }_{F=0}}-E^f{\left(D^{q^{\prime }}\right)}_{{\epsilon }_{F=0}}}{q^{\prime }-q}+\Delta E_{VBM}$ (4)

上式中， $E^f{\left(D^q\right)}_{{\epsilon }_{F=0}}$ 代表带电荷量为q的缺陷形成能， $E^f{\left(D^{q^{\prime }}\right)}_{{\epsilon }_{F=0}}$ 代表带电荷量 $q^{\prime }$ 的缺陷形成能，q和 $q^{\prime }$ 分别表示不同的价态。 $\Delta E_{VBM}$ 则是杂化泛函HSE修正之后价带顶下移的值。上式表明，要想求得缺陷转化能级，既要求得带边修正的值，还需要求得缺陷形成能(见表2和表3)。

Table 2. The band gap calculated by GGA-PBE and HSE methods and the band gap of experimental value

表2. GGA-PBE和HSE两种方法计算得到的禁带宽度与实验值的禁带宽度

Table 3. The position of the oxygen vacancy defect transition level relative to the valence band top

表3. 氧空位缺陷转化能级相对于价带顶的位置

3.3. 光学性质计算

利用带边修正方法得到更为准确的能带结构以及缺陷转化能级，利用FNV修正方法修正带电缺陷的缺陷形成能。在得到上述结果后，基于位形坐标图求得对应缺陷的光谱。

位形坐标模型 [23] 是关于电子和离子晶格振动总能量与离子平均位置(用一个坐标表示)相关的物理模型。也可以说，电子在某一状态时(基态或激发态)，离子晶格的势能曲线与离子平均位置之间的关系。将三维问题转化为一维的位形坐标图，结合上文中得到的缺陷转化能级以及缺陷形成能得到对应缺陷的光谱。如图3所示，本文给出了位形坐标模型与吸收和光发射过程示意图，简单描述电子–声子耦合过程，并给出一些相关参数 [24] 。

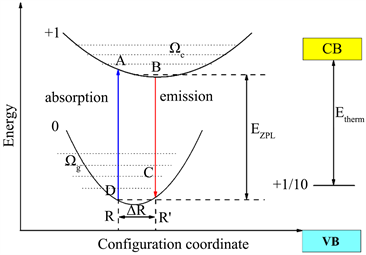
Figure 3. Configuration coordinate model and schematic diagram of absorption and light emission processes

图3. 位形坐标模型与吸收和光发射过程示意图

如图3所示，晶格弛豫过程中产生的能量损耗 $\Delta E_e$ 称为Franck-Condon [23] [25] 位移。图3中的 $E_{ZPL}$ 为基态与激发态平衡位置之间的能量差。由示意图可知，光吸收可表示为： $E_{abs}=E_{ZPL}+\Delta E_e$ ，有效参数 $\Delta Q$ 表示处于基态与激发态上的每个原子的相对原子质量与其在各个方向上产生的位移的乘积的和，可以表示为： ${\left(\Delta Q\right)}^2={\displaystyle {\sum }_{\alpha ,i}{m}_{\alpha }^{1/2}\Delta R_{\alpha ,i}}$ ， $\Delta R_{\alpha ,i}$ 表示弛豫过程中的原子在各个方向(i (x，y，z))上产生的位移。其中， $\alpha$ 表示原子种类， $m_{\alpha }$ 表示 $\alpha$ 原子的相对原子质量， $\Delta Q$ 可以表示为：

$\Delta Q=M^{1/2}\Delta R$

上式中， $\Delta R$ 可以表示为： ${\left(\Delta R\right)}^2={\displaystyle {\sum }_{\alpha ,i}\Delta R_{\alpha ,i}^2}$ 。

得到材料缺陷的光谱需要给出电子–声子相互作用。为此，引入黄昆因子 [26] 这个物理量，该物理量表示晶格弛豫能所折合的声子数，可以定义为：

$S_g=\frac{\Delta E_g}{\hslash {\omega }_g}$ ； $S_e=\frac{\Delta E_e}{\hslash {\omega }_e}$

上式中， ${\omega }_g$ 与 ${\omega }_e$ 分别表示基态与激发态的晶格有效振动频率。

引入黄昆因子S，更好地理解电子–声子耦合作用，并对光学过程中参与的声子数进行量化处理。根据弗兰克–康登原理，得到一维位形坐标图光吸收和发射进程涉及到的一些重要参数。基于第一性原理计算的归一化的发射光谱可以表达为 [24] ：

$L\left(\hslash \omega \right)={\displaystyle \underset{n}{\sum }{\text{e}}^{-s}\frac{s^n}{n!}{g}_{\sigma }\left(E_{ZPL}-\hslash {\omega }_{gn}-\hslash \omega \right)}$ (5)

上式中， $L\left(\hslash \omega \right)$ 是归一化函数，S为黄昆因子， $g_{\sigma }$ 为高斯函数， $\sigma$ 表示高斯函数展宽因子， $E_{ZPL}$ 表示零声子线。

在假设相同频率的简谐振子的情况下可以得到归一化吸收强度，吸收谱的表达式 [24] [27] ：

$f\left(h\nu \right)={\displaystyle \underset{p=-\infty }{\overset{\infty }{\sum }}\delta }\left(E_0-p\hslash \omega -h\nu \right)W_p$ (6)

上式中， $W_p$ 可以表达为：

$W_p=\exp \left[-\left(2\bar{n}+1\right)S\right]{\left[\left(\bar{n}+1\right)/\bar{n}\right]}^{p/2}\times I_p\left(2S{\left[\left(\bar{n}+1\right)\bar{n}\right]}^{1/2}\right)$ (7)

上式中， $I_p$ 是一个修正的贝塞尔函数，上式中， $\bar{n}$ 被定义为：

$\bar{n}={\left[\exp \left(\hslash \omega /kT\right)-1\right]}^{-1}$ (8)

S表示黄昆因子，可由 $S=\frac{\Delta E}{\hslash \omega }$ 获得，k表示玻尔兹曼常数，T表示温度， $E_0$ 表示热跃迁能级(相对于CBM)，它的值等于 $E_{ZPL}$ 的数值， $\hslash \omega$ 表示声子能量， $h\nu$ 表示光子能量，ΔE表示基态或激发态弛豫能。 $\omega$ 表示有效振动频率。

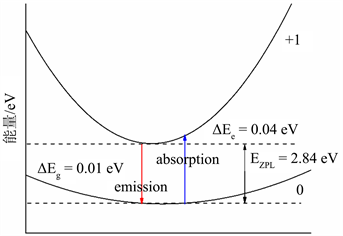
在得到缺陷形成能与缺陷转化能级的基础上，计算得到一维位形图，如图所示，图4(a)和图4(b)分别为F心和F⁺心的一维位形坐标图，费米能级设置在价带顶。图中的抛物线分别对应基态和激发态。 $\Delta E_e$ 是激发态的晶格弛豫能， $\Delta E_g$ 则是基态的晶格弛豫能。蓝色实线代表吸收能量，红色实线代表发射能量， $E_{ZPL}$ 是零声子线。图4(a)中，费米能级设置在价带顶。表4给出了用于氧空位光谱计算的有效参数，根据式5与式6，给出了氧空位的归一化光谱图，如图4所示，蓝色实线为F心的吸收谱，红色虚线为F⁺心的吸收谱。从图5中可以看出，F心吸收峰位于2.85 eV (435 nm)，F⁺心吸收峰则位于2.80 eV (443 nm)。

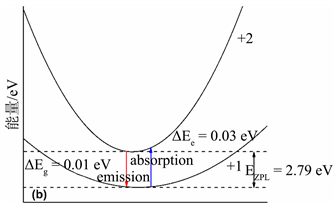(a)(b)

Figure 4. (a) Coordinates of the electronic transition configuration of the F center; (b) Electronic transition configuration coordinates of F⁺ center

图4. (a) F心的电子跃迁位形坐标图；(b) F⁺心的电子跃迁位形坐标图

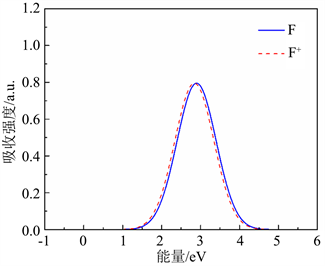
Figure 5. Absorption spectra of oxygen vacancy F and F⁺ centers

图5. 氧空位F心和F⁺心的吸收谱

Table 4. Valid parameters for the calculation of oxygen vacancy spectra

表4. 用于氧空位光谱计算的有效参数

在得到F心和F⁺心的吸收谱之后，计算了对应的发射谱。如图6所示，黑色实线代表F心的发射谱，红色虚线代表F⁺心的发射谱。可以看出F心的发射峰位于2.83 eV (438 nm)，F⁺心的发射峰位于2.78 eV (446 nm)。经过计算，推测F心发射峰位于2.83 eV (438 nm)，F⁺心发射峰位于2.78 eV (446 nm)，为实验研究光谱提供理论参考。计算结果与3.07 eV吸收谱与Pinto等人 [28] 的结果基本一致。计算结果表明：氧空位的转化能级靠近导带底，是浅能级，也是该材料导电电子的主要来源，是该材料n型导电的原因，这与实验结果一致 [29] [30] 。

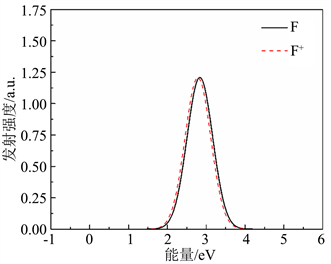
Figure 6. Emission spectra of oxygen vacancy F and F⁺ centers

图6. 氧空位F心和F⁺心的发射谱

4. 结论

本文基于第一性原理并结合GGA-PBE计算方法，对BTO晶体的完整结构以及含缺陷结构的不同价态分别进行结构优化，在结构优化的基础上又分别进行静态计算，并计算了BTO晶体中本征点缺陷的缺陷形成能，结合HSE带边修正得到较为准确的缺陷转化能级。根据计算得到的缺陷形成能以及缺陷转化能级，计算结果表明，氧空位是浅施主能级，是该材料n型导电的原因。根据计算结果，本文预测2.85 eV (435 nm)和2.80 eV (443 nm)的吸收峰分别起源于F心和F⁺心；2.83 eV (438 nm)和2.78 eV (446 nm)的发射峰分别归于F心和F⁺心。本文的研究为研究缺陷光谱提供了理论方法。

参考文献

NOTES

^*通讯作者。