1. 引言
原子核由质子和中子构成,传统的观点认为原子核中的质子之间存在电磁力和引力,电磁力比万有引力强1035倍,核子要形成稳定的原子核,核子之间应该有第三种相互作用——核力 [1] 存在。
1935年,汤川秀树提出“介子论” [2] [3] [4] [5] ,他认为核子之间是由于交换介子而产生交互作用的。汤川秀树认为:只要核子几乎相撞,这种有重媒介粒子就会在核子之间产生、交换和吸收,为了产生核力,一个核子与另一个核子交换一个介子,第一个核子必须实际产生这个有重介子。对于1个短暂间隔
,体系的能量可能存在一不确定量
,以使
。在
内,以近乎光速飞行的粒子通过距离
,令R为核力程,并令核子体系的能量的不确定量等于所产生的介子的质量
。那么,从海森堡原理得出:
(1)
所以,介子的质量必为
,而
,由此得出:
(2)
式中,
为核交换时间,约为10−23 s。显而易见,核子发出1个介子,核子所包含的质能(大约1800 me)就要减少200 me。
介子理论存在的问题:1) 核子交换介子的过程应该是一个核子向空间四面八方发射介子,经空间传输后,部分介子被另一个核子吸收的过程,核子质量是介子质量的9.2倍,那么核子发射9个介子,就必须有一个介子与另一个核子发生作用,而核子之间的距离为1.6 × 10−15 m,核子半径为0.8 × 10−15 m,
,一个核子发射的介子不能保证与相邻核子发生作用。2) 核子向空间四面八方发射介子,作为原子核外围的核子,必定有一部分介子会发射到原子核外的空间,而这种介子是短程的,原子核不可能接收到原子核外的介子,介子质量是核子的1/9.2,按照汤川秀树的介子理论,原子核的质量将会出现明显下降。3) 核子要分离出这么大的粒子,吸收这么大的粒子,本身要产生介子位移1/9.2的位移,介子位移为1.6 × 10−15 m,核子位移为0.17 × 10−15 m,核子将处于剧烈动荡之中。4) 引力子和介子都是核子之间的传播子,重复了。
当然,核子与介子发生作用,作为偶然现象是完全可能的,但作为核子与核子中间的常态传播子,是存在问题的。
2. 核力和强力
量子力学和基本粒子学说 [6] 认为自然界一共存在四种力:引力、电磁力、弱力和强力。核力是原子核中质子和质子、质子和中子、中子和中子之间的作用力,是核子形成原子核的作用力;核子由夸克组成,强力是夸克之间的作用力,与核力不同,核力和强力是两个不同的概念。
3. 不同类型光线的光子 [7]
光子的传输形成电磁波,电磁波分为无线电波、红外线、可见光、紫外线、X射线、γ射线几种。
1) 无线电波一般是由导体内的自由电子被激发,在能量降低时发出光子。
2) 红外线、可见光、紫外线是由原子的价电子被激发到高能级后,向低能级跃迁时产生光子。
3) X射线由原子的内层电子激发–跃迁时产生光子。
4) γ射线来自于原子核内部,在原子核内涉及到放射性衰变、核裂变、聚变等过程中,有电子的产生和消亡时,常有γ光子伴随产生。同时,在高等粒子的碰撞、衰变、正反粒子湮灭时,也常常产生γ光子。
4. 典型的光子产生机理 [8]
原子都是由原子核和核外电子构成,核外电子可以处在不同的能级,电子在自己的固定轨道上绕核旋转,如图1。根据能量最低原理,电子总是首先填充能量较低的轨道,处于稳定的基态;当电子获得额外能量,它能够争脱核的束缚,向高能量轨道跃迁处于激发态,此时该电子可通过向外辐射光子的形式降低自身能量回到基态,而光子的能量正好等于两个轨道能量之差。光的频率取决于电子跃迁的能级差。光子是光线中携带能量的粒子。在上述的时间反演过程中光子能够被吸收,此时分子、原子或原子核从低能级向高能级跃迁。
5. 电磁力的传递过程
电子跃迁产生光子,光子是一种带有负电荷的微粒子(微光子)。电场、磁场、电磁场的本质是微光子在场中不同的运动形式产生的。微光子的直线运动形成电场,微光子的环形运动形成磁场,微光子的圆柱螺旋线(摆线)运动形成电磁场。电场和磁场是微光子的不同运动形式的表现。电场、磁场、电磁场统一的对外作用是对处于场中的带电粒子有力的作用,带电粒子带负电时,这个力的方向与微光子的运行方向相反,带电粒子失去电子带正电时,这个力的方向与微光子的运行方向相同,力的大小符合库伦定律 [9] ,也就是力的大小与微光子的电量和场中带电粒子电量的乘积成正比。
(3)
式中,K为库仑常数(静电力常量) 9.0 × 109 Nm2/C2。
6. 质子之间不存在电磁力
6.1. 半导体中的空穴
图2是半导体中的空穴 [10] 示意图。半导体中有两种载流子:自由电子和空穴。在热力学温度零度和没有外界能量激发时,价电子受共价键的束缚,晶体中不存在自由运动的电子,半导体是不能导电的。但是,当半导体的温度升高(例如室温300 K)或受到光照等外界因素的影响时,某些共价键中的价电子获得了足够的能量,足以挣脱共价键的束缚,跃迁到导带,成为自由电子,同时在共价键中留下相同数量的空穴。空穴带正电,与电子的电荷量相同。由于空穴的存在,临近共价键中的价电子很容易跳过去填补这个空穴,从而使空穴转移到邻近的共价键中去,而后,新的空穴又被其相邻的价电子填补,这一过程持续下去,就相当于空穴在运动。带负电荷的价电子依次填补空穴的运动与带正电荷的粒子作反方向运动的效果相同,因此我们把空穴视为带正电荷的粒子。在半导体理论中,空穴和空穴中间不存在库伦斥力。
6.2. 质子之间不存在电荷斥力
图3是原子核结构示意图。任何非接触作用都是场的作用。在原子核中,电子可以自由运动,电子带负电荷,电子的跃迁产生光子。和半导体中的空穴一样,失去电子的中子形成质子,质子形式上带正电荷,带正电荷的质子不可移动。质子并不会发出带负电荷的光子,形成电磁场,相邻的质子也不会处于对方质子形成的粒子场中,不会受对方质子场中传播子作用产生斥力。因此,原子核中,质子之间并不存在电荷斥力。

Figure 3. Schematic diagram of nucleon structure
图3. 核子结构示意图
7. 引力可以覆盖核结合能
核子之间距离为1.6 × 10−15 m,与核子直径相同,因此相邻核子不能作为质点处理,核子之间的引力不能直接使用牛顿万有引力公式计算。
7.1. 引力的传递过程 [11]
物质由分子构成,分子由原子构成,原子由原子核和围绕原子核旋转的电子构成,电子质量太小,暂不考虑电子的引力问题,原子核由质子和中子组成,质子和中子质量相等,质子带正电,中子不带电,不考虑带电问题,把质子、中子统称为核子,不同的原子质量不同,但基本上与核子数量成正比,这样物质的质量基本上与核子数量成正比,可以认为核子是物质的最小质量单位,量子力学和基本粒子观点认为,引力是交换引力子产生的,具体的就是核子发出引力子,在空间传播后遇到其它核子,与其它核子发生共振,引力子被其它核子吸收,形成引力。核子发出引力子,在空间形成引力能量波,根据共振原理,引力能量波与核子发生共振时,传输的能量最大,可以推断,引力能量波的波长λ等于核子的直径(半径为r)。
(4)
引力能量波在空间的传输速度为光速c = 3 × 108 m,则引力能量波的频率为:
(5)
周期为:
(6)
引力能量波携带的能量为:
(7)
引力能量波的波长λ为1.6 × 10−15 m,在原子核内部,核子与核子之间的距离与引力能量波的波长在同一数量级,核子之间的距离对引力能量波与核子的共振影响不能忽略。核子之间的距离小于1.6 × 10−15 m时,由共振曲线可以知道,核子之间产生能量交换的概率不大,设想核子为弹性球,此时随着距离的减小,核子之间的斥力会明显增加;当核子之间的距离等于1.6 × 10−15 m时,核子本身的弹性斥力消失,引力能量波与核子的共振达到最强,引力能量波与核子交换能量最大,表现的引力也最大;当核子之间的距离大于1.6 × 10−15 m时,核子本身的弹性斥力不存在,由共振曲线可以知道,核子之间产生能量交换的概率迅速下降,表现为引力也明显下降;当核子之间的距离为1.5 × 1.6 × 10−15 m时,核子之间能量交换接近于0,引力也接近于0;随后随着第二个周期的到来,引力子能量交换的概率会逐步增加,当核子之间的距离为2 × 1.6 × 10−15 m时,达到第二个高峰,但是此时引力子交换的能量已经下降到第一个高峰的十分之一,以后随着距离的增加,引力会迅速下降。
7.2. 核子之间传递的能量
图4中,p是核子P0不断发出大量引力子形成的一条引力线,P1是处在引力线上的另一个核子,核子的半径为r,两个核子之间的距离为R,核子P0发出的引力线以波的形式传播,波长为2r。当核子P1与引力能量波发生共振时,核子吸收引力子的概率最大,当核子P1与引力能量波未发生共振时,核子吸收引力子的概率迅速下降,核子吸收引力子的概率大小符合共振曲线。
图5是以核子P0为中心的球坐标系,A是核子P0发出的一个引力在核子P1球面上的位置,设核子P0发出的引力子总数量为N0,我们来计算能与P1发生作用的引力子数。设P0A = x,P0C = R,则:

Figure 4. Gravitation and energy transfer between nucleons
图4. 核子之间的引力和能量传递
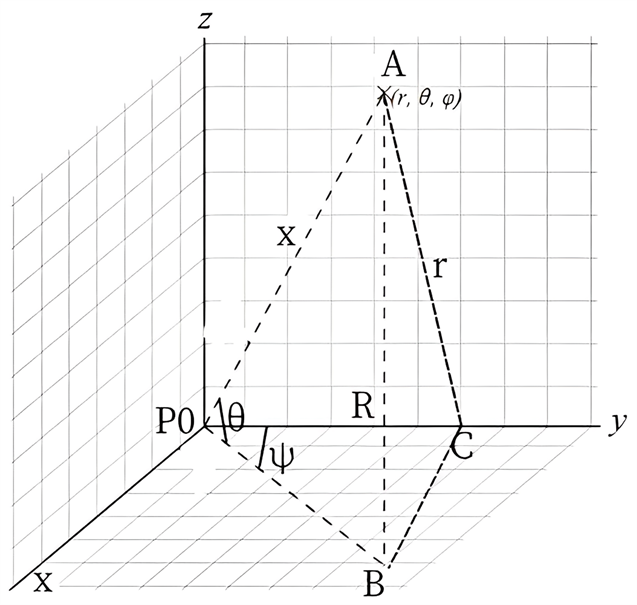
Figure 5. Nucleon in the spherical coordinate system
图5. 球坐标系的核子
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
引力线穿过核子P1的长度P13 P14为:
(16)
设R = kr,则P0发出的引力线穿过核子P1引起共振的核子总数为:
(17)
式中,S是积分面积,N0是核子P0单位1 s内发出的核子总数,πr2/4πR2是扫过核子P1的引力线占核子P0整个引力线的比例,sin()是表示引力能量波按正弦函数传播,核子P0发出的引力子与核子P1发生作用的概率按正弦函数规律变化。将上式简化:
(18)
几种特例:
当θ = 0、ψ = 0、k = 1时,N = 0;
当θ = 0、ψ = 0、k = 2时,N = 1/16N0;
当θ = 0、ψ = 0、k = 3时N = 0;
当θ = 0、ψ = 0、k = 4时,N = 1/64N0。
当k = 2时,为相邻2核子的情况,N2为相邻两核子交换引力子数量:
(19)
(20)
上式可以通过数值模拟求近似解(求解过程略),由此可以得出单位时间1 s内,相邻核子之间交换引力子数量为单个核子发出引力子数量的比值:
(21)
理想情况下,单个核子上一个周期发射引力子回到基态,下一个周期吸收引力子到激发态,同时另外一个核子上一个周期吸收引力子到激发态,下一个周期发射引力子回到基态,两个相邻核子之间每个周期都会交换引力子,这样两个相邻核子之间1 s内交换的能量为:
(22)
按照传统引力势能公式计算,核子P1处在核子P0引力场中的引力势能为:
(23)
这个值差得太多了,可见在微观距离上传统引力公式不适用。
原子核是核子凭借核力结合在一起构成的,要把它们分开,也需要能量,这就是原子核的结合能 [12] 。自然组成原子核的核子越多,它的结合能就越高。结合能与核子数之比,即一个原子核中每个核子结合能的平均值,为平均结合能,也叫比结合能。平均结合能越大,原子核中核子结合得越牢固,原子核越稳定。原子核的相对稳定性可以用结合能解释。反应堆所发出的能量,归根结底是由原子核结合能提供的。图6是部分原子核的结合能和平均结合能。
由一个质子和一个中子构成,也就是两个相邻的核子构成,
的结合能为2.224 MeV,公式(22)是在理想情况下,计算的相邻核子之间交换引力子传递的能量为33 MeV,说明质子和中子之间的引力完全可以覆盖质子和中子间的结合能。由2个核子的结合能可以反推核子单位时间1 s内核子实际发出引力子的数量:
(24)
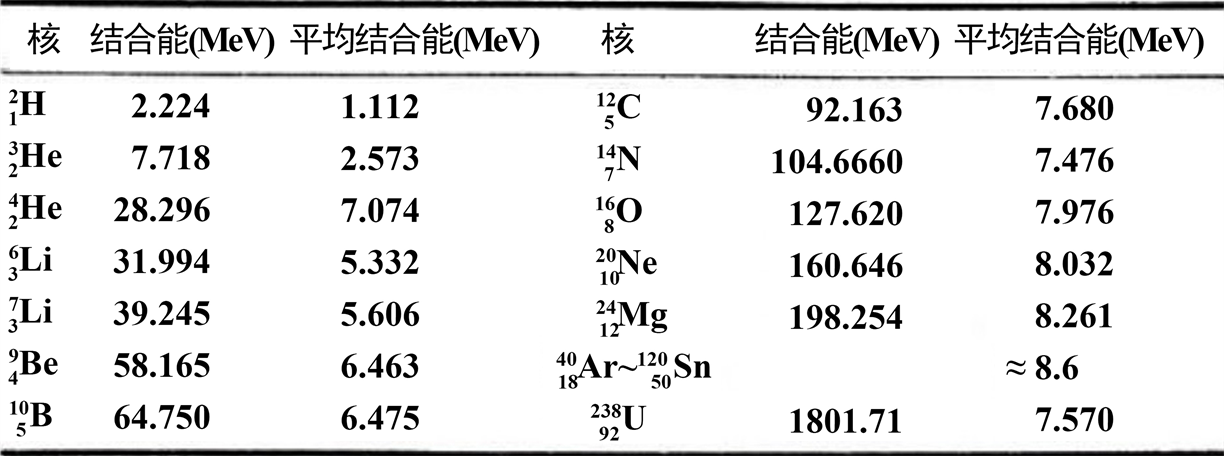
Figure 6. Binding energy and average binding energy of some atomic nucleus
图6. 部分原子核的结合能和平均结合能
由2个质子和1个中子构成,也就是3个核子构成,
的结合能为7.718 MeV,3个相邻的核子由3组两两相邻的核子组成,它们之间在理想情况下,通过引力传递的总能量为3 × 33 MeV = 99 MeV,可以得到同样的结果:3核子之间的引力完全可以覆盖3核子之间的结合能。
由2个质子和2个中子构成,也就是4个核子构成,
的结合能为28.296 MeV,4个相邻的核子由底层3个核子、上层1个处在3核子中间的核子组成,4个核子由6组两两相邻的核子组成,在理想情况下,它们之间通过引力传递的总能量为6 × 33 MeV = 198 MeV,同样地:4核子之间的引力完全可以覆盖4核子之间的结合能。
对于5个以上的核子,它的结构会出现隔层核子。隔层电子的典型排列是中间三个核子组成等边三角形,两面各一个核子都处于三个核子的中间,如图7。图8是隔层核子在球坐标系中的位置,图中AF为棱边都为2r正三棱锥的高。

Figure 7. Schematic diagram of compartment nucleus structure
图7. 隔层核子结构图示意图

Figure 8. Spacer nucleon the spherical coordinate system
图8. 球坐标系中的隔层核子
(25)
(26)
(27)
设N3.266为隔层核子交换引力子数量,由公式(18)可知:
(28)
同样地,可以用数值模拟的方法求解:
(29)
(30)
还有一个因素,核子A发出的引力子经过核子B、C、D,到达核子E,此时A发出的引力子有相当一部分已经被B、C、D吸收,只有剩余部分引力子到达E,因此A对E的引力子能量交换估计为相邻两核的0.2054/2 = 0.1027,为相邻两核子交换能量的十分之一。
(31)
核子应该是密接结构,在多于4个核子的原子核中,每个核子至少会与三个其它核子相邻,再加上隔层核子能量的互相传递,核子之间的总能量传递为:
(32)
式中,n为核子数量,m为隔层核子数量。对于数量很多的核子组成的原子核,还会有隔2层核子的情况,此时隔2层核子之间传递的能量更小。核子之间传递能量的大小与核子结构紧密相关。
图9是常用核结合能统计图。由公式(32)可以看出,核子之间通过引力子(引力)传递的能量可以完全覆盖核结合能。
8. 讨论
本文通过核子结合能推算的核子单位时间1 s发射的引力子数量为:1.26 × 1022,这个需要通过多核子结合能作进一步核实。多核子传递的引力能量应该根据原子核结构进行计算,这是一个比较复杂的过程。
9. 结论
光子(传输电磁力的玻色子)是在电子跃迁中产生的,它是一种带有负电荷的微粒子。电场、磁场、电磁场的本质是微光子在场中不同的运动形式形成的。微光子的直线运动形成电场,微光子的环形运动形成磁场,微光子的圆柱螺旋线(摆线)运动形成电磁场。电场和磁场是微光子运动形式的不同表现。电场、磁场、电磁场统一的对外作用是对处于场中的带电粒子有力的作用,带电粒子带负电时,这个力的方向与微光子的运行方向相反,带电粒子失去电子带正电时,这个力的方向与微光子的运行方向相同,力的大小与微光子的电量和带电粒子电量的乘积成正比。任何不接触的相互作用都是通过场的作用实现的,有电子跃迁的地方可以发出光子,形成电磁场,没有电子跃迁的地方,不会发出光子,也不会形成电磁场。原子核中的质子不会发出光子,它只吸收核外电子发出的光子,质子不发出光子,不会互相处在质子形成的电磁场中,就像半导体中失去电子的空穴之间不会产生斥力一样,质子之间也不会产生相互的斥力。核子(质子和中子的统称)是物质的最小质量单位,每个核子每时每刻都在不停地发出引力子,大量的引力子形成引力线,引力线以能量波的形式传播形成引力场,当引力线形成的引力能量波遇到处在引力场中的其它核子时,引力能量波与核子发生共振,引力子被核子吸收,引力子的能量全部转移给这个核子,形成引力。引力能量波和核子共振传输最大的能量,可以推断引力能量波的波长为核子的直径1.6 × 10−15 m,引力能量波以光速传播,可以推断引力能量波的频率为1.875 × 1023 hz,引力能量波每个周期携带能量6.626 × 10−34 J (普朗克常数),引力能量波单位时间1 s携带的能量为1.24 × 10−10 J,也就是775 MeV,核子之间的距离小于1.6 × 10−15 m时,由共振曲线可以知道,核子之间产生能量交换的概率很小,核子本身的弹性斥力增加,此时随着距离的减小,核子之间的引力明显下降,斥力会明显增加;当核子之间的距离等于1.6 × 10−15 m时,核子本身的弹性斥力消失,引力能量波与核子形成共振,引力能量波与核子交换能量最大,表现的引力也最大;当核子之间的距离大于1.6 × 10−15 m时,核子本身的弹性斥力不存在,由共振曲线可以知道,核子之间产生能量交换的概率迅速下降,表现为引力也明显下降;当核子之间的距离为1.5 × 1.6 × 10−15 m时,核子之间能量交换接近于0,引力也接近于0;随后随着第二个周期的到来,引力子能量交换的概率会逐步增加,当核子之间的距离为2 × 1.6 × 10−15 m时,达到第二个高峰,但是此时引力子交换的能量已经下降到第一个高峰的十分之一,以后随着距离的增加,引力会迅速下降。由以上分析可以看出,引力在微观距离上的表现完全符合核力的表现,引力传输的能量完全可以覆盖核结合能,由此可以推断核子之间的结合力就是引力,核子之间的结合能就是核子之间交换引力子的能量。
参考文献