具有媒体效应时滞的SEIRS-M传染病模型的动力学分析

Dynamic Analysis of SEIRS-M Epidemic Mod-el with Media Effect Delay

摘要: 为了研究在突发疫情中媒体信息对病毒传播的影响，本文建立了包含正负面信息影响的SEIRS-M模型，并且在模型中加入了一个媒体效应时滞。理论部分证明了模型解的非负性，得到了基本再生数和平衡点的表达式，分析了模型的稳定性以及Hopf分叉的存在性。最后通过数值模拟验证了理论结果，参数敏感性分析表明时滞越小疫情传播规模就越小，不同的信息贯彻率对疫情传播速度也有很大影响。因此，媒体应该在及时发布疫情相关信息的同时保障信息的质量，为群众提供有价值的信息从而增强人们的疾病预防意识，减少疫情传播规模。

Abstract: In order to study the influence of media information on virus transmission in an outbreak, a SEIRS- M model containing positive and negative information is established in this paper, and a media ef-fect delay is added to the model. In the theoretical part, the non-negative solution of the model is proved, the expressions of the basic regeneration number and the equilibrium point are obtained, and the stability of the model and the existence of Hopf bifurcation are analyzed. Finally, the theo-retical results were verified by numerical simulation. The parameter sensitivity analysis showed that the smaller the time delay, the smaller the epidemic transmission scale, and different infor-mation implementation rates also had a great impact on the epidemic transmission speed. There-fore, the media should release epidemy-related information in a timely manner and ensure the quality of information, so as to provide valuable information for the masses, so as to enhance peo-ple’s awareness of disease prevention and reduce the scale of epidemic transmission.

1. 引言

自20世纪末以来，全球公共卫生一直面临着传染病带来的安全隐患。传染病的流行具有不确定性高、破坏性大、隐蔽性强的特点，据世界卫生组织2022年统计，在全球范围内，流行病仍造成1020多万人死亡，占所有死亡人数的18% [1] 。疫情的爆发不仅威胁着人类的生命健康，对于经济发展、社会和国家繁荣稳定也有着重大影响。而随着信息技术的日益强大，各个媒体在网络、报纸和短信等平台发布疫情的相关新闻，使得人们以多元化及多样化的方式吸收信息。由于信息内容的不同以及人民群众主观意识的差异，媒体信息传播对于传染病的流行趋势和传播规模可能会产生积极或者消极的影响。因此，在面临突发重大疫情时如何有效利用媒体信息控制病毒传播具有重要研究意义。

一些研究为了量化媒体信息引入独立仓室，进行动力学分析研究媒体效应带来的影响。Greenhalgh等人 [2] 通过引入记忆衰退的时滞和媒体效应带来的延迟因素改进模型，结果表明增加媒体宣传的数量病毒传染率就会下降，意识方案的执行率越高病毒传播规模越小。Huo等人 [3] 提出了一种考虑媒介影响的新型SEIM流行病模型，模型分析结果表明媒介可以作为控制疫情发生和传播的良好指标。Zhou等人 [4] 提出了一个包含媒体信息累积量分区的确定性动力学模型来检验疾病进展与媒体报道的相互作用，得出了提高媒体报道率以及民众接收率能够减小感染高峰规模的结论。常星花 [5] 建立了带有脉冲响应和时滞的政策法规信息传染病模型来研究媒体信息对疾病传播的影响，研究发现疫情相关的政策法规信息能够很好地抑制群众的负面情绪从而减少疫情扩散规模。基于媒体效应来建立传染病模型还存在许多相关研究并且一直是一个挑战。

还有部分学者通过构造媒体函数表示接触感染率来研究媒体信息对控制疫情传播的影响。Xiao和Zhao [6] 研究建立了包含分段平滑感染率 $-\exp \left(-M\left(I,\text{d}I/\text{d}t\right)\right)$ 来扩展具有媒体报道的经典模型，分析了系统的动力学行为，结果表明媒体会延迟流行高峰并导致较低的爆发规模。Gao和Ruan [7] 研究了媒体报道和人体流动对斑块间传染病传播的影响，考虑媒体函数为 ${\beta }_i\left(I_i\right)=a_i-b_i{f}_i\left(I_i\right)$ ，结果表明媒体报道的确诊病例信息对当地人们的自我隔离行为具有影响从而降低感染率。张丽娟等人 [8] 针对媒体效应的传染病建立相应的反应扩散模型，研究重要参数如时滞、传染率和媒体效应等的影响。Cheng等人 [9] 通过构建基于网络的包含非单调发病率 $\theta /\left(1+\alpha {\theta }^2\right)$ 的SIQS模型来研究媒体效应对COVID-19传播的影响，研究发现媒体报道引起的心理因素变化和疫情扩散规模具有相关性。

综上所述，大部分研究只考虑了媒体信息带来的积极影响而忽略了消极层面。本文基于COVID-19疫情期间的媒体效应建立了包含正负面信息影响的传染病模型，引入两个独立分区表示正负面媒体信息累积量，并考虑到信息传播具有延迟的特点在模型中添加了一个媒体效应时滞。首先对模型进行理论分析包括系统解的性质、无病平衡点稳定性和分叉现象，其次进行数值仿真来分析媒体效应对疫情规模的影响。

2. 模型建立和动力学分析

2.1. 模型的建立

基于COVID-19具有潜伏期和无症状并且在此阶段仍有传染能力的特点，我们将总人群N划分为五类：无意识易感者S、受媒体影响采取保护措施的有意识易感者S_M、具有传染性但未确诊的感染者E、已被确诊强制隔离者I以及恢复者R，其中，E类人群包括处于潜伏期的感染者、无症状感染者以及有症状但未被确诊的感染者。S(t)，S_M(t)，E(t)，I(t)，R(t)分别表示各类人群在t时刻的数量，记 $N\left(t\right)=S\left(t\right)+S_M\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)$ 。

引入两个独立仓室表示有效信息量：M₁(t)表示在t时刻由于媒体播报产生的正面有效信息累积量，M₂(t)表示在t时刻由于媒体播报产生的负面有效信息累积量。媒体有效播报量与确诊病例数正相关，并且信息累积量具有耗散性。另外，由于媒体效应具有时间滞后性，我们假设t时刻的有效信息累积量与 $t-\tau$ 时刻的确诊人数有关。特别地，感染者I虽然具有传染性但已经被确诊并进行严格的隔离，所以不会感染易感者。S_M为在媒体信息驱动下主动隔离的有意识易感者被认为不会被感染，但是随着人们防护意识的消退和一些负面信息带来的消极影响，S_M中的人群会以概率 $\eta$ 再次转化为无意识易感者S。恢复者R经过一段时间后会重新变成具有隔离意识的易感类。模型示意图如图1：

Figure 1. State transformation diagram of model (1)

图1. 模型(1)的状态转化图

接下来给出传染病动力学模型：

$\{\begin{array}{l}\frac{\text{d}S\left(t\right)}{\text{d}t}=\Lambda +\eta S_M\left(t\right)-\left[\mu +\alpha f\left(t\right)+\beta cE\left(t\right)\right]S\left(t\right),\\ \frac{\text{d}{S}_M\left(t\right)}{\text{d}t}=\alpha f\left(t\right)S\left(t\right)+\epsilon R\left(t\right)-\left(\mu +\eta \right)S_M\left(t\right),\\ \frac{\text{d}E\left(t\right)}{\text{d}t}=\beta cS\left(t\right)E\left(t\right)-\left(\mu +\sigma \right)E\left(t\right),\\ \frac{\text{d}I\left(t\right)}{\text{d}t}=\sigma E\left(t\right)-\left(\mu +\delta +d\right)I\left(t\right),\\ \frac{\text{d}R\left(t\right)}{\text{d}t}=\delta I\left(t\right)-\left(\mu +\epsilon \right)R\left(t\right),\\ \frac{\text{d}{M}_1\left(t\right)}{\text{d}t}=u_{1}I\left(t-\tau \right)-u_0{M}_1\left(t\right),\\ \frac{\text{d}{M}_2\left(t\right)}{\text{d}t}=u_{2}I\left(t-\tau \right)-u_0{M}_2\left(t\right).\end{array}$ (1)

其中， $f\left(t\right)=\frac{M_1\left(t\right)-M_2\left(t\right)}{K+M_1\left(t\right)}$ 表示媒体报道信息对群众的正面影响函数。模型(1)满足初始条件：

$\{\begin{array}{l}S\left(0\right)>0,S_M\left(0\right)\ge 0,E\left(0\right)\ge 0,I\left(0\right)\ge 0,R\left(0\right)\ge 0,M_1\left(0\right)\ge 0,M_2\left(0\right)\ge 0;\\ S\left(\theta \right)>0,S_M\left(\theta \right)\ge 0,E\left(\theta \right)\ge 0,I\left(\theta \right)\ge 0,R\left(\theta \right)\ge 0,M_1\left(\theta \right)\ge 0,M_2\left(\theta \right)\ge 0,\theta \in \left[-\tau ,0\right].\end{array}$ (2)

模型中参数描述见表1：

Table 1. Descriptions of the model (1) parameters

表1. 模型(1)的参数说明

2.2. 系统的动力学分析

2.2.1. 模型解的非负性

通过对模型(1)各个状态变量的解进行分析，我们可以得到以下定理：

定理1 对于任意的 $t\ge 0$ ，模型(1)的解S(t)，S_M(t)，E(t)，I(t)，R(t)，M₁(t)，M₂(t)都是非负的。

证明 由初始条件(2)已知：

$\begin{array}{l}S\left(0\right)>0,S_M\left(0\right)\ge 0,E\left(0\right)\ge 0,I\left(0\right)\ge 0,R\left(0\right)\ge 0,M_1\left(0\right)\ge 0,M_2\left(0\right)\ge 0\\ S\left(\theta \right)>0,S_M\left(\theta \right)\ge 0,E\left(\theta \right)\ge 0,I\left(\theta \right)\ge 0,R\left(\theta \right)\ge 0,M_1\left(\theta \right)\ge 0,M_2\left(\theta \right)\ge 0,\theta \in \left[-\tau ,0\right]\end{array}$

那么对于 $t>0$ ，我们需证： $S\left(t\right)>0,S_M\left(t\right)>0,E\left(t\right)>0,I\left(t\right)>0,R\left(t\right)>0,M_1\left(t\right)>0,M_2\left(t\right)>0$ 。

定义 $\varpi =\sup \left\{t>0:S\left(t\right)>0,S_M\left(t\right)>0,E\left(t\right)>0,I\left(t\right)>0,R\left(t\right)>0,M_1\left(t\right)>0,M_2\left(t\right)>0\right\}$ ， $\varpi >0$ ， $t\in \left(0,\varpi \right)$ 。有如下两种情形：

① 如果 $\varpi =+\infty$ ，则定理1成立；

② 如果 $0<\varpi <+\infty$ ，则对于 $0<t<\varpi$ ，模型的解都是正的，而当 $t>\varpi$ 时， $S\left(\varpi \right),S_M\left(\varpi \right),E\left(\varpi \right),I\left(\varpi \right)$ $M_1\left(\varpi \right),M_2\left(\varpi \right)$ 中至少存在一个解小于等于零。

根据模型(1)有 $S^{\prime }\left(t\right)+\left[\mu +\alpha f\left(t\right)+\beta cE\left(t\right)\right]S\left(t\right)=\Lambda +\eta S_M\left(t\right)$ ，使用积分法求解可得：

$\begin{array}{l}S\left(t\right)={\text{e}}^{-{\displaystyle {\int }_0^t\mu +\alpha f\left(w\right)+\beta cE\left(w\right)\text{d}w}}\left({\displaystyle {\int }_0^t\left(\Lambda +\eta S_M\left(w\right)\right){\text{e}}^{{\displaystyle \int \mu +\alpha f\left(t\right)+\beta cE\left(t\right)\text{d}t}}\text{d}w+C}\right)\\ S\left(\varpi \right)=L_{1}S\left(0\right)+L_1{\displaystyle {\int }_0^{\varpi }\left(\Lambda +\eta S_M\left(t\right)\right){\text{e}}^{{\displaystyle \int \mu +\alpha f\left(t\right)+\beta cE\left(t\right)\text{d}t}}\text{d}t}\end{array}$

其中， $L_1={\text{e}}^{-{\displaystyle {\int }_0^{\varpi }\mu +\alpha f\left(t\right)+\beta cE\left(t\right)\text{d}t}}>0$ ，当 $0<t<\varpi$ 时， $S_M\left(t\right)>0,E\left(t\right)>0,S\left(0\right)>0$ ，且 $S\left(0\right)>0$ ，所以 $S\left(\varpi \right)>0$ 。

根据模型(1)有 ${M^{\prime }}_1\left(t\right)+u_0{M}_1\left(t\right)=u_{1}I\left(t-\tau \right)$ ，使用积分法求解可得：

$\begin{array}{l}{M}_1\left(t\right)={\text{e}}^{-{\displaystyle {\int }_0^t{u}_0\text{d}w}}\left({\displaystyle {\int }_0^t{u}_{1}I\left(w-\tau \right){\text{e}}^{{\displaystyle \int u_0\text{d}t}}\text{d}w+C}\right)\\ ={\text{e}}^{-{\displaystyle {\int }_0^t{u}_0\text{d}w}}\left({\displaystyle {\int }_{-\tau }^{t-\tau }{u}_{1}I\left(w-\tau \right){\text{e}}^{{\displaystyle \int u_0\text{d}t}}\text{d}\left(w-\tau \right)+C}\right)\\ M_1\left(\varpi \right)=L_2{M}_1\left(0\right)+L_2{\displaystyle {\int }_{-\tau }^{\varpi -\tau }{u}_{1}I\left(t-\tau \right){\text{e}}^{{\displaystyle \int u_0\text{d}t}}\text{d}\left(t-\tau \right)}\\ =L_2{M}_1\left(0\right)+L_2{\displaystyle {\int }_{-\tau }^0{u}_{1}I\left(\theta \right){\text{e}}^{{\displaystyle \int u_0\text{d}\left(\theta +\tau \right)}}\text{d}\left(\theta \right)}+L_2{\displaystyle {\int }_0^{\varpi -\tau }{u}_{1}I\left(\theta \right){\text{e}}^{{\displaystyle \int u_0\text{d}\left(\theta +\tau \right)}}\text{d}(\; \theta \; )}\end{array}$

其中， $L_2={\text{e}}^{-{\displaystyle {\int }_0^{\varpi }{u}_0}\text{d}t}>0$ ，当 $-\tau <\theta <0$ 时， $I\left(\theta \right)\ge 0$ ，当 $0<\theta <\varpi -\tau$ 时， $I\left(\theta \right)>0$ ，且 $M_1\left(0\right)\ge 0$ ，所以 $M_1\left(\varpi \right)>0$ 。

同理可得 $S_M\left(\varpi \right)>0,E\left(\varpi \right)>0,I\left(\varpi \right)>0,R\left(\varpi \right)>0,M_2\left(\varpi \right)>0$ ，该结果与上述情形②相违背，所以， $\varpi =+\infty$ ，定理1成立。

2.2.2. 基本再生数及平衡点分析

在流行病系统中有一种特殊的无病平衡，另 $E=0,I=0$ 经过计算得到无病平衡点 $P_0=\left(S^0,S_M^0,E^0,I^0,R^0,M_1^0,M_2^0\right)=\left(\frac{\Lambda }{\mu },0,0,0,0,0,0\right)$ 。当时滞 $\tau =0$ 时，基于下一代矩阵方法 [10] ，我们可以得到模型(1)的新增感染者矩阵 $\mathcal{F}$ 与感染者流出矩阵 $\mathcal{V}$ ：

$\mathcal{F}=\left[\begin{array}{c}\beta cSE\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$ ， $\mathcal{V}=\left[\begin{array}{c}\left(\mu +\sigma \right)E\\ \left(\mu +\delta +d\right)I-\sigma E\\ \left(\mu +\alpha f+\beta cE\right)S-\Lambda -\eta S_M\\ \left(\mu -\eta \right)S_M-\alpha fS-\epsilon R\\ \left(\mu +\epsilon \right)R-\delta I\\ u_0{M}_1-u_{1}I\\ u_0{M}_2-u_{2}I\end{array}\right]$ ，

$\mathcal{F}$ 和 $\mathcal{V}$ 在无病平衡点 $P_0$ 处的Jacobi矩阵分别为：

$F=\left(\begin{array}{cc}\beta c{S}^0& 0\\ 0& 0\end{array}\right)$ ， $V=\left(\begin{array}{cc}\mu +\sigma & 0\\ -\sigma & \mu +\delta +d\end{array}\right)$ ，

所以，模型(1)的基本再生数为 $R_0=\frac{\beta c\Lambda }{\mu \left(\mu +\sigma \right)}$ 。

在传染病模型中还有另外一种平衡即地方病平衡，通过分析可以得到以下定理：

定理2 当 $R_0>1$ 时，模型(1)存在唯一的地方病平衡点 $P_1=\left(S^{*},S_M^{*},E^{*},I^{*},R^{*},M_1^{*},M_2^{*}\right)$ 。

证明 根据模型(1)得到地方病平衡点：

$\begin{array}{c}{P}_1=\left(S^{*},S_M^{*},E^{*},I^{*},R^{*},M_1^{*},M_2^{*}\right)\\ =\left(\frac{\Lambda +\eta S_M^{*}}{\mu +\alpha f^{*}+\beta c{E}^{*}},\frac{\epsilon R^{*}+\alpha f^{*}{S}^{*}}{\mu +\eta },\frac{\left(\mu +\delta +d\right)I^{*}}{\sigma },\frac{\sigma E^{*}}{\mu +\delta +d},\frac{\delta I^{*}}{\mu +\epsilon },\frac{u_1{I}^{*}}{u_0},\frac{u_2{I}^{*}}{u_0}\right)\end{array}$ ，

根据地方病平衡点各状态的表达式，通过一些计算步骤得到如下关于 $I^{*}$ 的二次方程：

$A_1{I}^{*}{}^{{}^2}+A_2{I}^{*}+A_3=0$ ，

其中

$\begin{array}{c}{A}_1=\sigma \eta \beta c\epsilon \delta u_1-\left(\mu +\sigma \right)\left(\mu +\eta \right)\left(\mu +\epsilon \right)\left(\mu +\delta +d\right)\beta c{u}_1\\ A_2=\beta c\left(\mu +\eta \right)\left(\mu +\epsilon \right)\left(\Lambda \sigma u_1-(\mu +\delta +d)K{u}_0\right)+\alpha \left(\mu +\epsilon \right)\left(u_1-u_2\right)\left(\left(\mu +\sigma \right)-\sigma \left(\mu +\eta \right)\right)\\ +\sigma \eta \beta c\epsilon \delta u_{0}K-\left(\mu +\eta \right)\left(\mu +\epsilon \right)\left(\mu +\sigma \right)u_1\\ A_3=\sigma u_{0}K\left(\mu +\eta \right)\left(\mu +\epsilon \right)\left(\beta c\Lambda -\mu \left(\mu +\sigma \right)\right)\\ =\sigma u_{0}K\left(\mu +\eta \right)\left(\mu +\epsilon \right)\mu \left(\mu +\sigma \right)\left(R_0-1\right)\end{array}$

因为 $A_1<0$ ，根据韦达定理可知如果 $A_3>0$ 则 $I^{*}$ 存在唯一正实根，即当 $R_0>1$ 时，模型(1)存在唯一的地方病平衡点 $P_1$ 。

定理3 如果 $R_0<1$ ，则模型(1)的无病平衡点 $P_0$ 是局部渐近稳定的；当 $R_0>1$ 时，模型(1)的无病平衡点 $P_0$ 是不稳定的。

证明 系统的稳定性可以根据Routh-Hurwitz准则 [11] 来判别，模型(1)在无病平衡点处的Jacobi矩阵为：

$J\left(P_0\right)=\left(\begin{array}{ccccccc}-\mu & \eta & -\beta c{S}^0& 0& 0& -\frac{\alpha S^0}{K}& \frac{\alpha S^0}{K}\\ 0& -\left(\mu +\eta \right)& 0& 0& \epsilon & \frac{\alpha S^0}{K}& -\frac{\alpha S^0}{K}\\ 0& 0& \beta c{S}^0-\left(\mu +\sigma \right)& 0& 0& 0& 0\\ 0& 0& \sigma & -\left(\mu +\delta +d\right)& 0& 0& 0\\ 0& 0& 0& \delta & -\left(\mu +\epsilon \right)& 0& 0\\ 0& 0& 0& u_1& 0& -u_0& 0\\ 0& 0& 0& u_2& 0& 0& -u_0\end{array}\right)$ ，

解得矩阵 $J\left(P_0\right)$ 的特征值：

$\begin{array}{l}{\lambda }_1={\lambda }_2=-u_0,\\ {\lambda }_3=-\mu ,\\ {\lambda }_4=-\left(\mu +\eta \right),\\ {\lambda }_5=-\left(\mu +\epsilon \right),\\ {\lambda }_6=-\left(\mu +\delta +d\right),\\ {\lambda }_7=\left(\mu +\sigma \right)\left(R_0-1\right).\end{array}$

可见，当 $R_0<1$ 时， ${\lambda }_7<0$ ，矩阵 $J\left(P_0\right)$ 的所有特征值均具有负实部，所以模型(1)在无病平衡点 $P_0$ 处是局部渐近稳定的；反之 $R_0>1$时， ${\lambda }_7>0$ ， $P_0$ 是不稳定的。

2.2.3. 地方病平衡点的稳定性及Hopf分叉

本小节主要讨论在时滞 $\tau >0$ 的情况下，模型(1)在地方病平衡点处的稳定性以及Hopf分叉现象。

定理4 当 $\tau \in \left[0,{\tau }_0\right)$ 时，模型(1)在地方病平衡点 $P_1$ 处是局部渐近稳定的，

${\tau }_0=\frac{1}{w_0}\arctan \left(\frac{\left(q_{3}w-q_1{w}^3\right)\left(p_1{w}^6-p_3{w}^4+p_5{w}^2-p_7\right)-\left(q_4-q_2{w}^2\right)\left(w^7-p_2{w}^5+p_4{w}^3-p_{6}w\right)}{\left(q_4-q_2{w}^2\right)\left(p_1{w}^6-p_3{w}^4+p_5{w}^2-p_7\right)-\left(q_{3}w-q_1{w}^3\right)\left(w^7-p_2{w}^5+p_4{w}^3-p_{6}w\right)}\right)$ 。

证明 $\tau >0$ 时，模型(1)在地方病平衡点 $P_1$ 处的线性化系统表示为：

$\frac{\text{d}u}{\text{d}t}=F_{1}u\left(t\right)+F_{2}u\left(t-\tau \right)$ ， (3)

其中：

$F_1=\left(\begin{array}{ccccccc}-\left(\mu +b_1+b_2\right)& b_3& -b_9& 0& 0& -b_7& b_8\\ b_2& -\left(\mu +b_3\right)& 0& 0& \epsilon & b_7& -b_8\\ b_1& 0& b_9-b_4& 0& 0& 0& 0\\ 0& 0& \sigma & -b_5& 0& 0& 0\\ 0& 0& 0& \delta & -b_6& 0& 0\\ 0& 0& 0& 0& 0& -u_0& 0\\ 0& 0& 0& 0& 0& 0& -u_0\end{array}\right)$ ，

$F_2=\left(\begin{array}{ccccccc}0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& u_1& 0& 0& 0\\ 0& 0& 0& u_2& 0& 0& 0\end{array}\right)$ ，

$b_1=\beta c{E}^{*},b_2=\alpha M_1^{*},b_3=\eta M_2^{*},b_4=\mu +\sigma ,b_5=\mu +\delta +d,b_6=\mu +\epsilon ,b_7=\alpha S^{*},b_8=\eta S_M^{*},b_9=\beta c{S}^{*}$ 。

根据 $F_1$ ， $F_2$ 计算得到线性化系统(3)的特征方程：

${\lambda }^7+p_1{\lambda }^6+p_2{\lambda }^5+p_3{\lambda }^4+p_4{\lambda }^3+p_5{\lambda }^2+p_6\lambda +p_7+\left(q_1{\lambda }^3+q_2{\lambda }^2+q_3\lambda +q_4\right)=0$ ， (4)

式中，

$\begin{array}{l}{p}_1=B_1+B_6\\ p_2=B_7+B_1{B}_6+B_2+b_1{b}_9\\ p_3=B_1{B}_7+B_2{B}_6+B_3+B_8\\ p_4=B_2{B}_7+B_3{B}_6+B_4+B_9\\ p_5=B_3{B}_7+B_4{B}_6+B_{10}-b_1{b}_3\sigma \epsilon \delta \\ p_6=B_4{B}_7+B_5{B}_6+B_{11}-2u_0{b}_1{b}_3\sigma \epsilon \delta \\ p_7=B_5{B}_7+B_{12}-u_0{}^2{b}_1{b}_3\sigma \epsilon \delta \end{array}$ ， $\begin{array}{l}{q}_1=\sigma b_1\left(b_8{u}_2-b_7{u}_1\right)\\ q_2=q_1\left(\mu +u_0+b_6\right)\\ q_3=q_1\left(\mu u_0+\mu b_6+b_6{u}_0\right)\\ q_4=q_1\mu b_6{u}_0\end{array}$ ，

$\begin{array}{l}{B}_1=2u_0+\left(b_4-b_9\right)+b_5+b_6,\\ B_2=\left(b_4-b_9\right)\left(b_5+b_6\right)+b_5{b}_6+2u_0\left(b_4-b_9+b_5+b_6\right)+u_0^2,\\ B_3=\left(b_4-b_9+b_5+b_6\right)u_0^2+2\left[\left(b_4-b_9\right)\left(b_5+b_6\right)+b_5{b}_6\right]u_0+b_5{b}_6\left(b_4-b_9\right),\\ B_4=\left[\left(b_4-b_9\right)\left(b_5+b_6\right)+b_5{b}_6\right]u_0^2+2b_5{b}_6\left(b_4-b_9\right)u_0,\end{array}$

$\begin{array}{l}{B}_5=b_5{b}_6\left(b_4-b_9\right)u_0^2,\\ B_6=2\mu +b_1+b_2+b_3,\\ B_7={\mu }^2+\left(b_1+b_2+b_3\right)\mu +b_1{b}_3,\\ B_8=b_1{b}_9\left(\mu +b_3+b_5+b_6+2u_0\right),\end{array}$

$\begin{array}{l}{B}_9=b_1{b}_9\left[u_0^2+2\left(\mu +b_3+b_5+b_6\right)u_0+\left(\mu +b_3\right)\left(b_5+b_6\right)+b_5{b}_6\right],\\ B_{10}=b_1{b}_9\left[\left(\mu +b_3+b_5+b_6\right)u_0^2+2\left[\left(\mu +b_3\right)\left(b_5+b_6\right)+b_5{b}_6\right]u_0+b_5{b}_6\left(\mu +b_3\right)\right],\\ B_{11}=b_1{b}_9\left[\left[\left(\mu +b_3\right)\left(b_5+b_6\right)+b_5{b}_6\right]u_0^2+2b_5{b}_6\left(\mu +b_3\right)u_0\right],\\ B_{12}=b_1{b}_5{b}_6{b}_9\left(\mu +b_3\right)u_0^2.\end{array}$

令 $\lambda =iw\left(w>0\right)$ 代入特征方程(4)，分离其实部与虚部，得到如下超越方程：

$\{\begin{array}{l}{p}_1{w}^6-p_3{w}^4+p_5{w}^2-p_7=\left(q_4-q_2{w}^2\right)\cos \left(w\tau \right)+\left(q_{3}w-q_1{w}^3\right)\sin \left(w\tau \right)\\ w^7-p_2{w}^5+p_4{w}^3-p_{6}w=-\left(q_4-q_2{w}^2\right)\sin \left(w\tau \right)+\left(q_{3}w-q_1{w}^3\right)\cos \left(w\tau \right)\end{array}$ 。 (5)

将式(5)左右两边分别平方并相加，且令 $w^2=\xi$ 代入我们可以得到：

${\xi }^7+C_1{\xi }^6+C_2{\xi }^5+C_3{\xi }^4+C_4{\xi }^3+C_5{\xi }^2+C_6\xi +C_7=0$ ， (6)

这里，

$\begin{array}{l}{C}_1=p_1^2-2p_2,\\ C_2=p_2^2+2p_4-2p_1{p}_2,\\ C_3=p_3^2+2p_1{p}_5-2p_6-2p_2{p}_4,\\ C_4=p_4^2+2p_2{p}_6-2p_1{p}_7-2p_3{p}_5-q_1^2,\end{array}$

$\begin{array}{l}{C}_5=p_5^2+2p_3{p}_7-2p_4{p}_6-q_2^2+2q_1{q}_3,\\ C_6=p_6^2-2p_5{p}_7-q_3^2+2q_2{q}_4,\\ C_7=p_7^2-q_4^2.\end{array}$

如果 $C_i\left(i=1,2,3,4,5,6,7\right)$ 满足Routh-Hurwitz条件，则方程(6)没有正实根。此时，如果地方病平衡点 $P_1$ 存在则对 $\forall \tau >0$ 其渐近稳定，前提是 $\tau =0$ 时系统是稳定的。也就是说，在这种情况下，时滞 $\tau$ 不会对系统稳定性产生影响。

如果 $C_i\left(i=1,2,3,4,5,6,7\right)$ 不满足Routh-Hurwitz条件，不妨假设 $C_7<0$ ，此时，方程(6)至少存在一个正实根。即 $p_7^2<q_4^2$ 时，特征方程(4)有一对纯虚数根 $\pm i{w}_0$ ，根据 $w_0$ 由超越方程(5)我们可以得到 ${\tau }_n$ 的表达式：

${\tau }_n=\frac{1}{w_0}\arctan \left(\frac{\left(q_{3}w-q_1{w}^3\right)\left(p_1{w}^6-p_3{w}^4+p_5{w}^2-p_7\right)-\left(q_4-q_2{w}^2\right)\left(w^7-p_2{w}^5+p_4{w}^3-p_{6}w\right)}{\left(q_4-q_2{w}^2\right)\left(p_1{w}^6-p_3{w}^4+p_5{w}^2-p_7\right)-\left(q_{3}w-q_1{w}^3\right)\left(w^7-p_2{w}^5+p_4{w}^3-p_{6}w\right)}\right)+\frac{n\pi }{w_0}$ ，(7)

其中 $n=0,1,2,\cdots$ 。

由Butler引理可得，当 $\tau \in \left[0,{\tau }_0\right)$ 时，模型(1)的所有根都具有负实部，因此模型(1)在地方病平衡点 $P_1$ 处是稳定的。

接下来，判断系统(1)在经过 $\tau ={\tau }_0$ 时是否存在Hopf分叉行为。经过一系列计算与分析我们得到以下定理：

定理5 如果 $\Phi \left(w_0\right)>0$ ，系统(1)在 $\tau ={\tau }_0$ 处发生Hopf分叉现象。 $\Phi \left(w_0\right)$ 的表达式如式(8)所示。

证明 当系统存在Hopf分叉时，需满足 ${\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}_{\tau ={\tau }_0}\ne 0$ ，根据特征方程(4)可得：

${\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}=\frac{7{\lambda }^6+6p_1{\lambda }^5+5p_2{\lambda }^4+4p_3{\lambda }^3+3p_4{\lambda }^2+2p_5\lambda +p_6}{q_1{\lambda }^4+q_2{\lambda }^3+q_3{\lambda }^2{q}_4\lambda }{\text{e}}^{\lambda \tau }+\frac{3q_1{\lambda }^2+2q_2\lambda +q_3}{q_1{\lambda }^4+q_2{\lambda }^3+q_3{\lambda }^2{q}_4\lambda }-\frac{\tau }{\lambda }$ ，

$\begin{array}{l}Sgn{\left[\mathrm{Re}\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)\right]}_{\tau ={\tau }_0}=Sgn{\left[\mathrm{Re}{\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)}^{-1}\right]}_{\lambda =i{w}_0}\\ =Sgn[\mathrm{Re}\frac{\left(-7w_0^6+5p_2{w}_0^4-3p_4{w}_0^2+p_6\right)\cos \left(w_0\tau \right)-\left(6p_1{w}_0^5-4p_3{w}_0^3+2p_5{w}_0\right)\sin \left(w_0\tau \right)}{i{w}_0\left(q_4-q_2{w}_0^2\right)-\left(q_3-q_1{w}_0^2\right)w_0^2}\\ +\mathrm{Re}\frac{\left(-7w_0^6+5p_2{w}_0^4-3p_4{w}_0^2+p_6\right)\sin \left(w_0\tau \right)+\left(6p_1{w}_0^5-4p_3{w}_0^3+2p_5{w}_0\right)\cos \left(w_0\tau \right)}{i{w}_0\left(q_4-q_2{w}_0^2\right)-\left(q_3-q_1{w}_0^2\right)w_0^2}i\\ +\mathrm{Re}\frac{-3q_1{w}_0^2+q_3}{i{w}_0\left(q_4-q_2{w}_0^2\right)-\left(q_3-q_1{w}_0^2\right)w_0^2}+\mathrm{Re}\frac{2q_2{w}_0}{i{w}_0\left(q_4-q_2{w}_0^2\right)-\left(q_3-q_1{w}_0^2\right)w_0^2}i]\\ =Sgn[\frac{\left(D_1{D}_3+D_2{D}_4\right)\sin (w_0\tau )+\left(3q_1{w}_0^2-q_3\right)+2D_1{q}_2{w}_0}{D_1^2+D_2^2}]\end{array}$

其中，

$\begin{array}{l}{D}_1=w_0\left(q_4-q_2{w}_0^2\right),D_2=\left(q_3-q_1{w}_0^2\right)w_0^2,\\ D_3=-7w_0^6+5p_2{w}_0^4-3p_4{w}_0^2+p_6,D_4=6p_1{w}_0^5-4p_3{w}_0^3+2p_5{w}_0\end{array}$

由超越方程(5)计算得到：

$\sin \left(w_0\tau \right)=\frac{D_2\left(p_1{w}_0^7-p_3{w}_0^5+p_5{w}_0^3-p_7{w}_0\right)-D_1\left(w_0^8-p_2{w}_0^6+p_4{w}_0^4-p_6{w}_0^2\right)}{D_1^2+D_2^2}$ 。

设

$\Phi \left(w_0\right)=\left(D_1{D}_3+D_2{D}_4\right)\sin \left(w_0\tau \right)+\left(3q_1{w}_0^2-q_3\right)+2D_1{q}_2{w}_0$ ， (8)

如果 $\Phi \left(w_0\right)>0$ ，那么有 $Sgn{\left[\mathrm{Re}\left(\frac{\text{d}\lambda }{\text{d}\tau }\right)\right]}_{\tau ={\tau }_0}>0$ ，所以系统(1)在 $\tau ={\tau }_0$ 处出现Hopf分叉行为。

3. 数值模拟

在本小节中，为了观察系统的动力学特性，借助Matlab软件根据模型(1)进行一些数值模拟。各个状态变量的初始值选取湖北省2020年2月1日的数据。其中， $E\left(0\right)$ 的取值为2月8日与2月1日确诊人数相减。参数取值如2.1小节表1所示，均来自于文献 [5] 或者设定。

$\begin{array}{l}{N}_{Hubei}=5.927\times {10}^7,I\left(0\right)=9074,E\left(0\right)=18026,R\left(0\right)=215,\\ S\left(0\right)=N_{Hubei}-E\left(0\right)-I\left(0\right)-R\left(0\right),S_M\left(0\right)=0,M_1\left(0\right)=0,M_2\left(0\right)=0\end{array}$

首先，我们对模型(1)的路径图进行了模拟，结果如图2所示。结果显示感染者E和I的数量在100天左右之后趋于稳定状态，病毒将在湖北省发展成为地方病。此时根据选取的参数值计算得到基本再生数 $R_0=9.9>1$ ，系统(1)存在唯一地方病平衡点。为了研究 $R_0$ 的大小和疫情传播规模之间的关系，在其他参数值保持不变的情况下，通过修改感染率 $\beta$ 和检疫率 $\sigma$ 来改变 $R_0$ 进行模拟，结果如图3所示。结果表明，当 $R_0<1$ 时，确诊感染人数在50天之后衰减至零，此时系统(1)处于稳定的无病平衡状态。

Figure 2. Path diagram of model (1)

图2. 模型(1)路径图

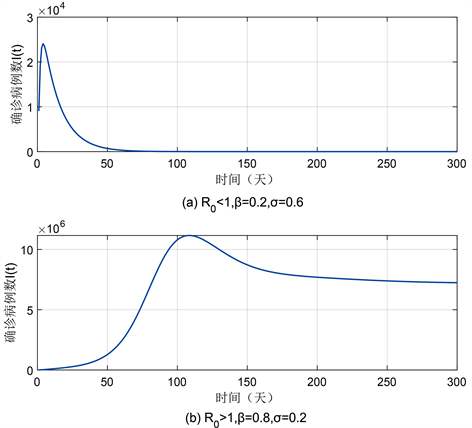
Figure 3. Graph of the relationship between I(t) and R₀

图3. 确诊感染人数与R₀的关系图

为了考察媒体的滞后性、媒体信息贯彻率对疫情扩散的影响，同时研究媒体信息带来的正负面不同效应，我们分别取不同的参数值进行敏感性分析，模拟结果如图4所示。

由图4(a)可知，当媒体效应不存在时间滞后性时，感染人数相比于考虑时滞的感染人数要少，且随着时滞的增加感染规模越大。为了更好的控制疫情扩散，媒体应当及时播报有效信息。图4(b)向我们展示了不同信息贯彻率下的感染者人数，当正面信息贯彻率 $u_1=0.9$ ，负面信息贯彻率 $u_2=0.1$ 时，疫情传播速度明显较其他情况下慢很多。

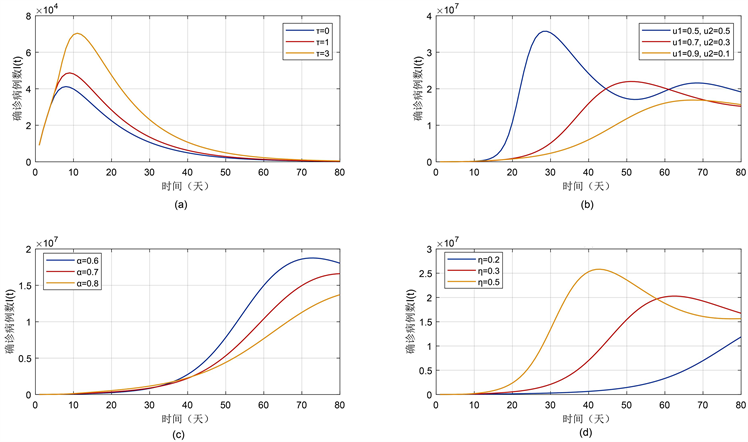
Figure 4. Influence of media information on the number of confirmed infections

图4. 媒体信息对确诊感染人数的影响

图4(c)和图4(d)分别描述了受媒体信息影响人们积极应对和消极应对的比例与I(t)的关系。可以看出，当接受到媒体信息后，人民群众积极采取保护措施的比例越高，感染者人数越少，而当媒体信息对人们产生的消极因素越高感染规模越大。媒体在及时发布信息的同时也要注意信息的质量问题，争取有效的增强人民群众的预防意识，从而达到减少疫情扩散规模的效果。

4. 总结

基于传染病仓室模型的思想，为了研究在突发疫情中媒体信息对病毒扩散的影响，本文建立了包含正负面信息影响的SEIRS-M模型。考虑到媒体信息的传播具有时间滞后性，我们在模型中对有效信息累积量的描述添加了一个时滞 $\tau$ 。理论部分证明了模型解的非负性，得到了基本再生数和平衡点的表达式，分析了模型的稳定性以及Hopf分叉的存在性。分析结果表明，当 $R_0<1$ 时，模型的无病平衡点 $P_0$ 是渐近稳定的；当 $R_0>1$ 时，模型具有唯一的地方病平衡点 $P_1$ ，并且在 $\tau \in \left[0,{\tau }_0\right)$ 时是渐近稳定的。最后通过数值模拟验证了理论结果，根据选取的参数值计算得到 $R_0=9.9>1$ ，模拟结果显示模型在大约100天后趋于稳定的地方病平衡状态。参数敏感性分析表明时滞 $\tau$ 越小疫情传播规模就越小，所以媒体需要及时发布信息，尽早播报疫情发展趋势以及预防措施等相关信息。另外，不同的信息贯彻率对疫情传播速度也有很大影响，随着正面信息贯彻率 $u_1$ 的增加，病毒的传播速度明显呈现降低趋势。因此，媒体注重信息播报及时性的同时要保障信息的质量，为群众提供有价值的正面信息，从而增强疾病预防意识，抑制疾病传播。

基金项目

国家自然科学基金项目(61672298)；中国博士后科学基金面上项目(2019M651917)。

NOTES

^*通讯作者。