基于ARIMA模型的山东省GDP的研究与预测

Research and Forecasting of GDP in Shandong Province Based on ARIMA Modeling

摘要: GDP是衡量一个国家或地区经济发展状况的重要指标，COVID-19流行期间，各地经济的发展均受到或大或小的影响，经济发展策略和经济体系需要进行调整，所以GDP预测研究更是显得尤为重要。因此，本文基于ARIMA模型，对山东省近年来的GDP进行拟合和预测。结果表明，山东省的经济一直处于稳定增长状态，受疫情影响增速变缓。预测结果显示，未来5年山东省GDP仍保持增长状态。最后根据预测结果对山东省发展提出合理的建议。

Abstract: GDP is an important indicator to measure the economic development of a country or region, during the COVID-19 epidemic, the development of the economy of each place is affected to a greater or lesser extent, the economic development strategy and the economic system need to be adjusted, so the GDP forecasting research is more important. Therefore, this paper is based on ARIMA model to fit and forecast the GDP of Shandong Province in recent years. The results show that the economy of Shandong Province has been in a stable growth state, and the growth rate has been slowed down by the epidemic. The prediction results show that the GDP of Shandong Province still maintains the growth state in the next five years. Finally, reasonable suggestions for the development of Shandong Province are made based on the prediction results.

1. 引言

山东省的经济发展状况一直处于全国前列，并且经济增长也一直处于稳定增长状态。即使在国家提倡高质量发展的情况下，山东省的经济依然呈现稳定增长态势，更是在2017年达到新的高峰。所以，拟合研究和预测山东省经济发展状况，既是对山东省自身的经济发展提供一些理论帮助，也是国家的区域经济进行一个研究和预测，从而对山东省的经济发展和政策制定提供一些思路。

GDP是反应一个国家或地区经济发展状况的重要指标，它和就业率、失业率、经济增长率、通货膨胀率等众多经济指标息息相关。想要了解一个地区的经济发展状况以及受影响程度，GDP是一个非常合适的经济指标。自从新冠疫情开始，GDP的增速明显放缓。为了今后更好更有效的持续发展，我们研究和预测GDP的发展与将来的走势情况，这对于了解经济发展情况并及时做出判断，从而提出有效的建议是很有必要的。

在此背景下，本文基于ARIMA模型，通过R软件，对山东省近年来的GDP进行了拟合和预测。通过分析可知，COVID-19的流行对山东省GDP的增长速度产生了影响。

2. 文献综述

近几年来，国内众多学者着手研究国内各地区GDP发展情况。关于GDP的理论和应用研究有很多，目前，学者们采用最多的研究方法是时间序列分析法。在近几年对各省、各地区的GDP研究中，王霞等(2021) [1] 等采用的是混频动态因子模型，将GDP预测频率从“季度”提高到“日度”，从而可以更加及时的判断当前经济的运行状况，制定更加具有时效性的经济政策。申佳帆和黄云开(2022) [2] 基于ARIMA模型和VAR模型，从单变量和多变量两个角度对云南省GDP进行拟合预测分析，研究结果表明ARI(1,1)模型、IMA(1,2)模型以及VAR(1)模型都很好的解释了云南省GDP发展的规律，但从预测角度ARI(1,1)模型和VAR(1)模型更优。杨智凯等(2021) [3] 采用时间序列方法建立ARIMA模型，预测了2020年桂林市的GDP，将预测值与真实值作比较，结果的相对误差在合理范围之内，最后利用ARIMA模型对桂林市未来5年的GDP进行了预测。查华和石舢(2022) [4] 基于ARIMA模型，选取江苏省1975年到2020年的生产总值，然后对未来两年的经济发展做出预测，研究结果表明，江苏省的经济处于稳步增长，但是2020年的经济发展受到疫情的影响，这为之后的发展规划提供了重要的参考依据。

通过阅读文献，我们发现很多学者对预测GDP经常采用的还是基于时间序列分析方法建立模型。时间序列分析法预测结果比较准确，模型构建简洁，对预测GDP十分有用。关于时间序列分析方法，学者们将其用于多个领域的价格预测研究。基于此，本文采用时间序列分析方法，选取山东省1975年~2020年的GDP数据，通过建立ARIMA模型，对山东省的GDP进行预测分析，以探究COVID-19流行期间对山东省GDP造成的影响，并根据预测结果对山东省未来发展提出合理建议。

3. 方法与数据

3.1. 模型方法

时间序列分析法预测结果比较准确，模型构建简洁，对预测GDP十分有用。本文采用ARIMA模型方法来进行GDP的分析预测。ARIMA模型一般是对平稳时间序列进行建模，对于非平稳序列，我们通过差分使之变得平稳，其中，I表示的就是差分。另外，AR表示的是自回归模型，MA表示的是移动平均模型。模型方法如下：

$\{\begin{array}{l}\varphi \left(B\right){\nabla }^d{x}_t=\theta \left(B\right){\epsilon }_t\\ E\left({\epsilon }_t\right)=0,Var\left({\epsilon }_t\right)={\sigma }_{\epsilon }^2,E\left({\epsilon }_t{\epsilon }_s\right)=0,s\ne t\\ E\left(x_s{\epsilon }_t\right)=0,\forall s<t\end{array}$

式中， ${\nabla }^d={\left(1-B\right)}^d$ ； $\varphi \left(B\right)=1-{\varphi }_{1}B-\cdots -{\varphi }_p{B}^p$ ，为平稳可逆ARMA(p,q)模型的系回归系数多项式； $\theta \left(B\right)=1-{\theta }_{1}B-\cdots -{\theta }_q{B}^q$ ，为平稳可逆ARMA(p,q)模型的移动平均系数多项式 [5] 。

模型建立好之后，还要对模型进行显著性检验。关于模型的显著性检验一般包括模型的显著性检验和模型参数的显著性检验。关于模型的显著性检验是检验模型是否有效，提取信息是否充分；参数的显著性检验是指模型中的每一个参数是否显著不为0。除此之外，还要对数据进行平稳性检验，一般选用ADF检验。

3.2. 数据来源与处理

本文首先以山东省以1975~2016年的GDP数据为训练集，预测未来四年的GDP发展趋势，将得到的预测值与真实值作比较，来检验模型的预测效果。如果所拟合的模型预测效果良好，那么我们可将该模型用于预测未来某期间内的GDP发展情况。本文中所用到的数据来自于均来自于山东省统计局网站中，2021年官方所发布的山东省统计年鉴。其中选用1975~2020年的山东省GDP数据。

根据时间序列的建模原则，对于获得的时间序列数据，我们首先要判断数据的平稳性。对于平稳性序列，我们可以直接对其建立模型，对于非平稳序列，我们可采用适当的差分运算，使其变得平稳之后，在对其进行建模分析。平稳时间序列一般分为两种，一是严平稳时间序列，另一种是宽平稳时间序列。严平稳序列一般只存在于理论之中，现实生活中我们所研究的大多还是宽平稳时间序列。在本文中，我们提到的平稳时间序列指的是宽平稳时间序列。

4. 建模分析过程

4.1. 模型的识别与定阶

模型的识别与定阶实际上就是确定ARIMA(p,d,q)模型中的p、d、q。ARIMA(p,d,q)模型是对平稳序列进行建模分析，当数据不平稳时，可通过差分处理使序列变得平稳，使序列平稳进行的差分的次数就是d的值。p和q的值则通过样本的自相关系数(ACF)和偏自相关系数(PACF)来确定，确定准则见表1：

Table 1. Model ordering

表1. 模型定阶

4.2. 模型的优化

在时间序列分析中对于平稳时间序列建模时，有时候我们可以对同一个平稳非白噪声序列建立多种模型，此时，我们需要选择最优模型来进行拟合分析。在选择最有模型时，一般根据AIC准则或者BIC准则来进行确定，判断规则是AIC或者BIC数值越小，说明模型拟合越好。

4.3. 模型的估计

对于模型的估计，我们常见的一共有三种方法，分别是矩估计，极大似然估计和最小二乘估计。在本文中，我们采用的是最小二乘估计所以在这里我们只详细介绍最小二乘估计。最小二乘估计：

在ARMA(p,q)模型场合，记

$\tilde{\beta }={\left({\varphi }_1,\cdots ,{\varphi }_p,{\theta }_1,\cdots ,{\theta }_q\right)}^{\prime }$

$F_t\left(\tilde{\beta }\right)={\varphi }_1{x}_{t-1}+\cdots +{\varphi }_p{x}_{t-p}-{\theta }_1{\epsilon }_{t-1}-\cdots -{\theta }_q{\epsilon }_{t-q}$

残差项为：

${\epsilon }_t=x_t-F_t(\; \beta \; ˜\; )$

残差平方和为：

$Q\left(\tilde{\beta }\right)={\displaystyle \underset{t=1}{\overset{n}{\sum }}{\epsilon }_t^2}={\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(x_t-{\varphi }_1{x}_{t-1}-\cdots -{\varphi }_p{x}_{t-p}+{\theta }_1{\epsilon }_{t-1}+\cdots {\theta }_q{\epsilon }_{t-q}\right)}^2}$

使得残差平方和达到最小的那组参数即为 $\tilde{\beta }$ 的最小二乘估计值。

4.4. 模型的拟合和预测

本文选取了1979~2020年的山东省GDP数据，数据来源于2021年的山东省统计年鉴。数据如表2所示：

Table 2. Shandong Province GDP in 1979-2020

表2. 山东省1979~2020年GDP

注：单位(亿元)。

首先，我们要判断数据的平稳性，在本文中，我们应用到的是时序图检验和单位根检验。首先，做出数据的时序图，如图1：

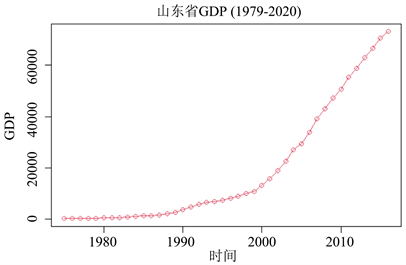
Figure 1. Timing diagram of the original sequence

图1. 原始序列时序图

通过时序图，我们发现GDP数据有明显的增长趋势，可以非常容易地可判断出GDP原始序列为非平稳序列。接下来我们对数列进行一阶差分处理。

进行一阶差分后，数据的时序图如图2所示：

Figure 2. Timing diagram after first-order differencing

图2. 一阶差分后时序图

由时序图可知，一阶差分后的数据还是存在轻微的增长趋势，接下来对数据进行单位根检验，来判断数据是否平稳，单位根检验结果如图3所示：

Figure 3. Unit root test results

图3. 单位根检验结果

由单位根检验结果可知，一阶差分后的P值均大于0.05，这表示此时数据仍为非平稳序列，所以需要继续对数据进行差分处理。二阶差分后，数据的时序图如图4所示：

Figure 4. Timing diagram after second-order differencing

图4. 二阶差分后时序图

通过观察时序图，我们可以发现，序列表现出了平稳的特征，二阶差分后的序列基本上围绕着均值上下波动，这说明了二阶差分对原始序列所蕴含的长期趋势提取的比较充分。接下来，我们可以再通过单位根检验，来进一步确定2阶差分后的数据是否平稳。单位根检验的输出结果如图5所示：

Figure 5. Unit root test results

图5. 单位根检验结果

由R软件的输出结果可知，二阶差分后，P值均小于0.05，可认为在95%的水平下，二阶差分后的序列为平稳性序列。

接下来，对二阶差分后的数据进行随机性检验。R的输出结果如图6所示：

Figure 6. Randomness test results

图6. 随机性检验结果

由R软件的输出结果可知，该序列可拒绝纯随机性的原假设，说明数据的波动有统计规律。由上述分析可知，二阶差分后的序列可通过平稳性检验和纯随机性检验，这说明二阶差分后，序列为平稳序列。接下来就可以对处理后的序列拟合ARIMA模型，并通过自相关系数和偏自相关系数为模型定阶。二阶差分后GDP的自相关图和偏自相关图如图7和图8所示：

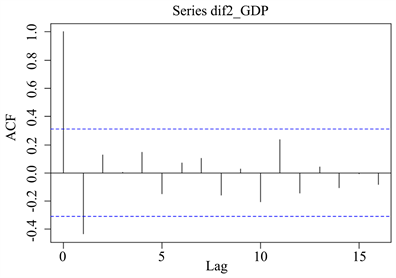
Figure 7. Sequence autocorrelation diagram

图7. 序列自相关图

Figure 8. Sequence biased autocorrelation plot

图8. 序列偏自相关图

根据自相关系数和偏自相关系数的特征，我们可以判断该序列自相关系数一阶截尾，偏自相关系数一阶截尾。我们可以拟合的模型有ARIMA(1,2,0)模型，ARIMA(0,2,1)模型，ARIMA(1,2,1)模型。根据AIC准则，BIC准则，我们选取这三个模型中最优的模型，R软件的输出结果如表3所示：

Table 3. Model optimization test results

表3. 模型优化检验结果

最小信息量准则检验显示，无论是使用AIC准则还是使用BIC准则，ARIMA(0,2,1)模型都要优于其他两个模型，所以，在本文中我们拟合的模型为ARIMA(0,2,1)模型。选择模型后，我们要对拟合模型进行显著性检验，其中包括，模型的显著性检验和参数的显著性检验。检验输出结果如图9所示：

Figure 9. Model significance test

图9. 模型显著性检验

由上图可知，模型的显著性成立。

接下来，检验参数的显著性，R的输出结果如表4所示：

Table 4. Significance test of parameters

表4. 参数的显著性检验

由参数的检验的输出结果可知，P值远远小于0.05，所以模型的参数的显著性检验成立。当模型通过检验后，就可以进行拟合与预测。模型的拟合结果如图10所示：

Figure 10. Model fitting results

图10. 模型拟合结果

由模型拟合的输出结果图可知，序列的真实值和拟合值基本一致，这说明我们所拟合的模型效果良好，可用该模型来进行预测。根据上述步骤，我们首先选取1979~2016年的山东省GDP数据作为测试集，用来预测未来四年(2017、2018、2019、2020年)的GDP数据，将预测值与真实值做对比，看相对误差的情况。

真实值与预测值的对比情况如表5所示：

Table 5. Comparison of relative errors

表5. 相对误差对比表

通过上表，我们可以看出，拟合模型的相对误差都在5%以下，说明我们建立的模型预测效果良好。相比较而言，2020年的相对误差稍微大了一点，我们猜测可能有两种原因，一是本文所拟合的ARIMA模型，可能更适合于短期预测；还有一种可能就是，2019年末，新冠疫情爆发，经济发展受到影响，可能导致了真实值与预测值相差有点大。但结果的相对误差仍然在合理范围之内。所以，我们可将模型用于预测山东省未来五年的GDP发展情况。预测结果如表6所示：

Table 6. GDP projections

表6. GDP预测值

通过观察预测结果，我们发现，山东省GDP依然是呈现增长趋势，但2021年、2020年的增长态势相较于之前，增速有点放缓，可能是新冠疫情对山东省的经济发展造成了一定的影响。

5. 结论

本文通过建立ARIMA模型，对山东省的GDP发展做出了一定的分析和预测。本文选取山东省统计局2021年公布的1979~2020年GDP数据为测试集，通过建立ARIMA模型，来预测未来五年的山东省GDP发展情况。从模型的测试情况来看，模型的相对误差全都在5%以下，说明拟合的该模型预测效果良好，预测结果有一定的参考价值。从最后预测的结果来看，山东省GDP仍然是保持了稳定增长的态势，但在疫情刚开始阶段对山东省经济也是产生了轻微的影响，疫情对经济发展的影响会持续多长时间，还需要我们进一步的研究探索。模型的预测结果也可为当地经济政策决定者提供一定的参考价值。同时，由测试集可知，随时预测年份的逐渐增加，预测的相对误差也有增加，说明随着预测年份的增加，预测的精度也发生了下降，反映出ARIMA模型可能更适合于短期预测的模型，还有一种可能性就是，2020年的预测精度下降，也有可能是新冠疫情对经济产生了影响，使得模型的预测精度下降了一些，这说明，疫情的发生，确实对经济的发展产生了影响。这提醒我们，面对经济现象的复杂性和不确定性，我们要提高管科的科学水平。减少决策的盲目性，就要及时预测，在疫情期间更是如此。所谓预测，也就是“鉴往知来”，综合各方方面的信息，运用定性和定量的方法，揭示经济运行的规律，据此来推断经济现象和经济未来发展的方向和结果。选取合适的经济模型，会让我们的研究结果更具参考价值。

通过本文的预测结果，我们得出以下几条结论：(一) 时间序列分析方法在用于预测价格波动和经济发展状况时，短期的预测效果良好，说明该方法非常适合短期预测；(二) ARIMA模型构建简单，准确定性较高，是值得我们好好学习并熟悉掌握的模型方法；(三) 根据模型的预测结果，我们可以清楚的看到，新冠疫情确实给经济发展带来了一定的影响。