1. 引言
1851年的巴黎,在法兰西共和国的先贤祠(国葬院)的大厅里,让·傅科进行一项有趣的实验 [1] 。傅科在大厅的穹顶上悬挂了一条67米长的绳索,绳索的下面是一个重达28千克的摆锤,摆锤的下方是巨大的沙盘。每当摆锤经过沙盘上方的时候,摆锤上的指针就会在沙盘上面留下运动的轨迹。按照日常生活的经验,这个硕大无比的摆应该在沙盘上面画出唯一一条轨迹。实验开始后,人们惊奇的发现,傅科设置的摆每经过一个周期的震荡,在沙盘上画出的轨迹都会偏离原来的轨迹,后经研究这种偏离是地球的自转造成的。在地球南半球这个偏转是逆时针方向,在地球北半球这个偏转是顺时针方向。图1为傅科摆的示意图。傅科摆实验首次为地球自转提供了天文学之外的证据。
莫里斯·阿莱是个著名的物理学大师,曾获得1988年诺贝尔经济学奖。1954年,他连续观测傅科摆长达30天,在这30天实验期间,他发现单摆摆动平面的转动速率在一天24小时之内有增、有减,特别是在这30天实验期间正好出现了一次日食,在没有日食出现时,傅科摆的摆动很正常,每小时转过的角度是11.3˚,但是在2.5个小时的日食期间,傅科摆的转动出现明显的异常,它的摆动平面突然反方向偏转了大约13.5˚,并在新的平面上一边摆动,一边转动,转动的速度还是每小时11.3˚,而日食即将过去时,傅科摆竟然又突然逆时针偏转13.5˚,也就是说,从那13.5˚的偏转面又回来了。后来在1959年,阿莱在57米深的地下再次重复了实验,得到了类似的结果。这就是日食期间的阿来效应 [2] [3] 。
后来,许多学者重复阿莱实验,结果出现了截然不同的结果。1954年苏格兰的观测无法支持阿莱的结论。在1961年发生的一次日全食时,三位罗马尼亚科学家的单摆实验观察到阿莱效应相同的结果。1965年意大利的观测无法支持阿莱的结论。1970年美国科学家萨克斯尔和艾伦对3月7日的日全食用扭摆检验阿莱效应,得到支持的结果。1991年发表在Physical Review D上的在芬兰做的观测也都宣称没有检测到阿莱效应。为了揭开这个困扰着物理学家们45年的谜团,1999年8月11日,NASA集结了来自4大洲的7国家的观测站,进行了一次跨国实验。但是没有公布结果。2010年发表在Physical Review D上阿根廷做的观测没有检测到阿莱效应。
日全食发生的前后,还有一个奇怪的现象吸引国际诸多科学家和媒体的关注:地球上的重力仪数据出现突然降低。1954年以来也出现过多次。1976年4月29日日环食时,我国在昆仑山口的引力效应观测 [4] ,没有发现明显的重力异常,但是在记录纸上发现3个微小倾斜;1987年9月23日日环食时,我国在乌鲁木齐进行引力观测 [5] ,未发现引力屏蔽与引力异常现象;1990年7月22日,当太阳刚从赫尔辛基东方地平线升起不久发生的日食期间,由芬兰的地球物理学家们在当地所做的实验,也未观察到地球引力有任何变化;1995年,位于印度海德拉巴的印度国家地球物理研究所的米什拉和拉奥,用一台非常准确的重力计测量出在日食期间地球引力的突然下降,记录到重力加速度的变化大约为12 × 10−6厘米·秒;1997年3月9日,我国黑龙江漠河地区发生日全食时,由王谦身 [6] [7] [8] 率领的中国地球物理学家小组,在此天文现象初亏和复原时,从重力计的读数测出重力加速度有5.7微伽[1伽 = 1厘米/秒2]的下降,这次观测到的结果如图2;刘少明等曾对1999年8月11日发生在欧洲的一次日全食做过详细的分析,当时曾在四个地点进行观测,并且每处都有两台重力仪,观测仪器中还有两台是精度很高的超导重力仪,但最终没有发现显著的重力异常;在2001年6月21日南部非洲赞比亚首都卢萨卡日全食时测得重力下降了4.5微伽;而在2002年12月4日澳大利亚的南澳大利亚州北部的盐湖沙漠地区日全食期间,记录到了重力下降1.5微伽;2009年7月22日的日食期间,中科院的物理学家们在杭州、湖州、上海、武汉四处进行了实验 [9] [10] [11] ,不过这次观测没有发现任何重力异常。
对于日食期间的阿莱效应和重力异常,不少学者做了研究,张登科老师2000年提出了日全食“重力异常”现象理论新解:“动量场与动量力”理论 [12] ,还有好多学者提出了不同学说,这里不多叙述。
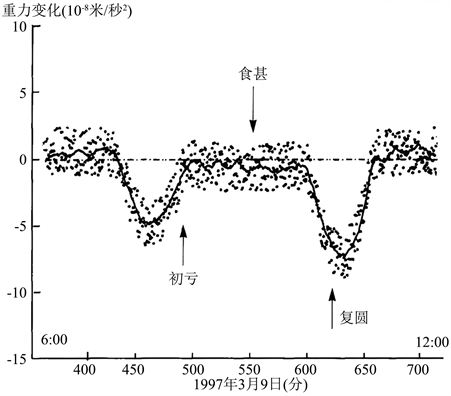
Figure 2. Actual measurement of gravity double valley
图2. 重力双谷实测图
2. 日食期间牛顿经典理论下的引力叠加
图3是日食发生前的日月位置图,图中S为太阳,M为月球,W为地表单位质量物质所在位置。
太阳(Sun),质量1.989 × 1030 kg,直径1.392 × 109 m,日地距离1.496 × 1011 m;月球(Moon),质量约7.342 × 1022 kg,直径约3.476 × 106 m,地月平均距离3.844 × 108 m。地球(Earth),质量5.972 × 1024 kg,半径6.371 × 106 m。
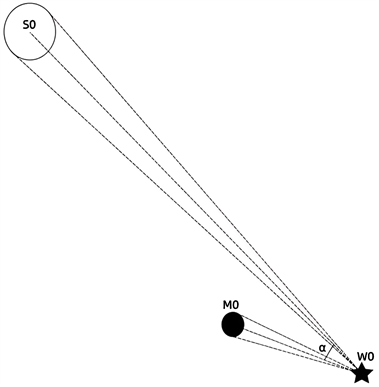
Figure 3. Gravitational superposition of the sun and the moon
图3. 日月的引力叠加
地球表面的物质受太阳引力、太阳离心力(二者和为太阳引潮力),月球引力、月球离心力(二者和为月球引潮力),地球引力,地表物质随地球自转向心力,重力共7个力的作用,常态下,这些力之间的夹角较大,发生日全食的时候,太阳地球月球处于同一直线上,月球在中间,此时月球与太阳对地球的引力叠加为引力最大的时候,其它力变化不大。
忽略地球半径的影响,按照万有引力公式,地面1 kg物体与太阳的万有引力(重力加速度)为:
(1)
太阳的视角为:
(2)
忽略地球半径的影响,按照万有引力公式地面1 kg物体与月球的万有引力(重力加速度)为:
(3)
月球的视角为:
(4)
日食初亏时,月球与太阳的视角相邻,此时地表物质受到月球与太阳的引力夹角为:
(5)
日月引力的合力为:
(6)
由于地表物质受到太阳的引力远远大于受到月球的引力,我们把太阳的引力作为参考。日食期间,地表单位物体受到的引力与只有太阳时受到的引力差为:
(7)
食甚时,此时月球与太阳的引力夹角为0,此时日月的和引力最大为:
(8)
与只有太阳引力时的差为:
(9)
当日食复原时,月球与太阳的视角相邻,此时月球与太阳的引力夹角为0.00917,日月的和引力为0.005962,此时与只有太阳引力时的差为:0.000034 N。日食期间地面1 kg物质受到日月的引力和平常只有太阳时的引力差曲线如图4。
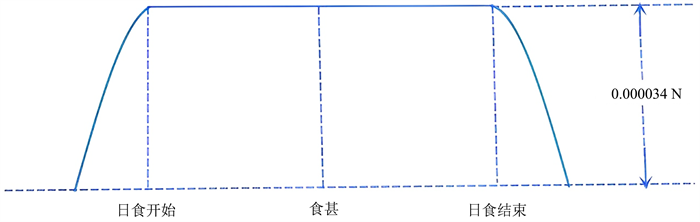
Figure 4. The difference between the gravitational force of the sun and the moon (Newton) and the gravitational force of the sun during a solar eclipse
图4. 日食期间日月合引力(牛顿)与太阳引力的差值
3. 日食期间量子引力理论下的引力叠加
量子引力概述 [13] [14] :物质由分子够成,分子由原子够成,原子由原子核和电子构成,原子核由中子和质子够成,中子和质子的质量基本相等,这里统称为核子,物体的质量基本与核子数量成正比,每个核子发出引力子,中心物体(星球)巨量的核子发出的引力子,绝大多数发射到星球外,形成引力线,引力线以波的形式传播形成引力场,有质量物体在引力场中运行时,会受到组成引力线的引力子作用,产生垂直于引力线方向的位移,在两条引力线中间运行的物体受到前后两条引力线作用的位移和方向不一样,这个垂直于引力线的位移,平行于物体运动方向的分量会影响物体的运行速度,垂直于物体运动方向的分量会影响物体的运行方向。根据力矩作用原理,运动物体受两条引力线作用产生的位移,垂直于物体运动方向的分量的合力矩会使运动物体产生一个垂直于物体运动方向的位移。对于远距离物体,其运动方向与引力线的夹角总是小于90˚,这个位移会使物体向中心物体偏转,这便形成了引力,随着物体运行距离的变化,其运动方向与引力线的夹角也会发生变化,当这个夹角一直小于90˚时,物体最终会与中心物体汇聚,形成更大的星球;物体运动方向与引力线的夹角接近90˚时,物体会绕中心物体运行形成行星;当物体运动方向与引力线夹角超过90˚时,物体前后引力线与物体作用的垂直方向合力矩产生的位移背向星球方向,此时中心物体(星球)的引力线对物体产生的作用不是引力,而是斥力。
在日食期间,月球处在太阳和地球中间,如图5。太阳发出射向地球的引力子在遇到月球时,由于月球几乎全部占用了太阳的全部锥形面积,所以这些引力子全部被月球吸收,此时处在地球上的日食范围内的物质,接受不到太阳发出的引力子,这些物质失去了太阳的引力,但同时月球上的物质发出的引力子补充了月球遮挡太阳的引力子,地球上接收到日月综合引力子数量不变,而且接受引力子的方向不变,所以此时地球上日食范围内的物质,收到日月总的引力子数量和只有太阳时的引力子数量一样,此时地球上的日食范围内的物质受到太阳和月球的引力之和等于只受到太阳时的引力。这和牛顿引力理论有明显区别。
这样在日食初亏时,地球上的物质会受到太阳和月球的共同引力,出现一个高峰,当日食发生时,由于引力子遮挡效应,地球上的物质受到日月引力的之和等于这些物质平常受到太阳的引力。当日食复原时,月球不再遮挡太阳发出的引力子,此时地球上发生日食范围内的这些物质,同时受到太阳和月球的引力,又会出现一个引力高峰,之后随着月球和太阳之间的夹角增大,地球上的对应物质受到的日月引力分散,这些物质受到的引力回复到常态。图6是发生日食时,地球表面单位物体受到日月引力之和与只有太阳引力的差,图中在日食前后出现2个引力高峰,相应的,地球表面单位物体的重力会出现双谷现象。

Figure 5. Graviton occlusion during a solar eclipse
图5. 日食期间的引力子遮挡

Figure 6. The difference between the gravitational force of the sun and the moon (quantum gravity) and the gravitational force of the sun during a solar eclipse
图6. 日食期间日月合引力(量子)与太阳引力的差值
4. 影响重力双谷和阿莱效应的主要因素
地表物质受到太阳引潮力(太阳引力与日地离心力矢量和)为:
(10)
地表物质受到月球引潮力(月球引力与地月离心力矢量和)为:
(11)
地表单位物体受到日月引潮力大小基本不变,但是各自的方向随日月的位置随时都在发生变化,它们在地平面和重力方向的合力也在随时变化。下面我们推导一下地表单位物体在地平面方向和重力方向的合力公式。
图7是地表1 kg物质所受地球重力的情况,图中AB为物体受到地球的引力,CB为地球自转的向心力,GB为物体的重力。
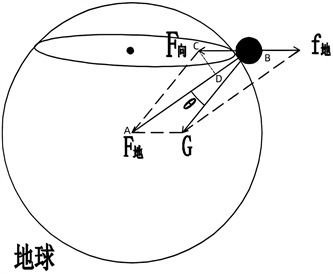
Figure 7. The angle between the object’s gravity and centripetal force
图7. 物体的重力和向心力之间的夹角
地球自转是地球的一种重要运动形式,自转的平均角速度ω为7.292 × 10−5弧度/秒,在地球赤道上的自转线速度为466米/秒。地球绕自转轴自西向东的转动。
设物体所在纬度为β,地球为标准圆,半径为rE,在纬度给定的情况下,地球自转半径为:
(12)
地表单位重力物质随地球自转的向心力:
(13)
单位质量物体受地球的万有引力为
(14)
单位物体的重力为:
(15)
(16)
设地表单位物质重力与地球的引力夹角为θG
(17)
(18)
在发生日食期间,可以认为太阳S,月球M,地表单位物质W和地心E处在同一个平面。
图8是物质W在日食初亏时的受力情况示意图,图中h是日食初亏时太阳的地平高度角,角度范围为0˚~90˚。β0是引力的地平方位角(引力在地面投影与W0地球自转方向的夹角),取值范围为±90˚,考虑南半球的话,这个力的方向正好相反。

Figure 8. The effect of inclination on the gravitational double valley
图8. 地球表面物质的受力分析
为了便于计算多个力的合力,我们把地表单位物质所受力分别按地平方向和重力方向分解,然后再分别计算合力。
设太阳地平高度角为h,这时物体受到地球引力和日地引力的夹角θS可以按正弦定律计算。
(19)
物体受到地球引力和地月引力的夹角θM为:
(20)
物体受到太阳的引力FSW为,
(21)
(22)
物体受到地球绕太阳运行的离心力为,
(23)
物体受到月球的引力FMW为:
(24)
(25)
物体受地月系统绕行的离心力,
(26)
这4个力在重力方向上的合力为:
(27)
这4个力在地平方向上的合力为:
(28)
重力的异常总是需要有一个参考值,而地表物质和日月位置在不断的发生变化,随着这3者位置的不同,物质重力也在不断地发生微小变化,目前计算重力并没有地表物质和日月位置的统一标准,各位研究者计算和选择地表物质和日月位置的数据不一样,最后参考的重力曲线和参数也不一样。图9是月球轨道及黄白交角示意图,在地球坐标系中,白道面与黄道面有5.145396度的夹角,忽略这个夹角的影响,我们把地平高度角和纬度不变的情况下,日食发生前,月球不同的位置作为参考点,这样可以反映日食前和日食期间引力峰值的突变大小,设物体与月球引力与物体与太阳引力的夹角为
,这时地月引力与地表单位物体的地球引力之间的夹角为:

Figure 9. Schematic diagram of lunar orbit and yellow-white intersection angle
图9. 月球轨道及黄白交角示意图
(29)
地表单位物体在重力方向上的合力为:
(30)
地表单位物体在地平方向上的合力为:
(31)
日食初亏时与参考点之间的重力差为:
(32)
简化后:
(33)
日食初亏时与参考点之间的地平面的作用力之差为:
(34)
简化后:
(35)
地表单位物体受到力的地平方向分量会对傅科摆摆锤产生影响,设β0是太阳引力的地平方位角。
日食期间对摆锤的速度影响为:
(36)
日食期间对摆锤的方向影响为:
(37)
通过上面推导,我们可以对不同情况下,地表单位质量物质的重力变化和地平方向合力的变化进行数据模拟。
图10为数据模拟部分截图。表中第一列为日月地主要参数,第2列为地平高度角,第3列为物质W所处纬度,第4~5为地表物质w的重力与地球引力的夹角,第6列为参考点(n = 2)物质引力与地月引力夹角,第7列为月食初亏时物质引力与地月引力夹角,ΔF ⊥ 1为月食初亏与参考点之间的重力差值,ΔF//1为月食初亏与参考点之间在地平面的分量差值。由表可以看出:地平高度角在0.34906585 (20˚)~1.134464014 (65˚)之间时,重力差值达到1 uGal以上,地平高度角为0.785398163 (45˚),纬度为1.4853529864 (85˚)时,重力差值最大为1.533 uGal。此时对于测量精度在2~3 uGal的测重仪,无法测到重力的变化。由表可以看出,物质所处纬度对重力差值影响不大。对于地平平面的分力,由表可以看出,地平高度角大于0.698131701 (40˚),各力在地平分量的合力差值大于1 × 10−6 N,此时重力变化会对傅科摆的速度或者方向变化应该较大,事实上傅科摆的摆锤速度变化不易觉察,相对的它的方向变化容易观察,而方向的变化量与方位角的正弦成正比,所以日食发生时,不是所有的地方都可以观测到阿莱效应,只有地平高度角大于40˚,地平方位角大于30˚的地区容易观察到阿莱效应。据“月球地平高度的变化规律解析”作者周义钦老师 [15] 推算,“月球平均每天东移约13˚”,阿莱观察到日食前后,傅科摆偏转13.5˚,就是受到月球引潮力的影响所致。
同样的,可以选n = 7进行数据模拟,由模拟结果可以看出:地平高度角在0.34906585 (20˚)~1.134464014 (65˚)之间时,重力差值达到6 uGal以上,地平高度角为0.785398163 (45˚),纬度为1.4853529864 (85˚)时,重力差值最大为9.174 uGal。从n = 1和n = 7模拟结果对比可以看出,发生日食时,测量重力异常的参考重力曲线对测量结果影响较大,其次发生日食时,地表观测点的地平高度角影响比较大。
5. 讨论
随着时间的变化,太阳、月球、地球的位置不断在发生变化,地表物质受到太阳引潮力和月球引潮力的方位也在不断发生变化,作为受到二者引潮力影响的地表物质的重力也在发生不断变化,要测量地表物质重力的变化,一个重力变化参考曲线和参数非常重要,这个需要广大学者的共同研究与讨论。
6. 结论
地表物质除受到地球引力、地球自转离心力外,还会受到太阳引力、日地离心力、月球引力、地月离心力的共同作用,平常这些力的方向偏离比较大,当日食初亏时,地表物质受到太阳和月球的离心方向没有大的变化,但是物质受到太阳和月球引力的方向几乎一致,这时日月引力的合力达到峰值,在日食期间,太阳发出的引力子,部分被月球吸收,此时地球表面物质收到太阳引力子减少,月球发出的引力子补充了太阳的引力子,地面物质收到日月的共同引力子数量与单独太阳的引力子数量相同,此时地表物质受到日月的合力与单独太阳的引力相同,当日食复原时,月球逃出太阳的阴影区,此时不存在引力子遮挡问题,地面上的物质受到日月引力的合力最大为第二高峰,随后随着月球与太阳夹角的增大,引力的合力减小恢复到常态。在日食期间,地面上的物质受到日月的引力出现双峰,相应的的重力出现双谷现象。在地平高度角大于40˚,地平方位角大于30˚的地区容易观察到阿莱效应;通常太阳、月亮、地表物质的位置在不断地发生变化,这就造成地表物质受到日月引潮力不断发生变化,再加上各地经纬度的不同,就很难形成统一的引潮力标准曲线和参数。日食期间观测点的地平高度角在20˚~65˚之间时,重力差值较大,地平高度角为45˚,重力差值会达到最大。重力差值的大小与重力异常的参考重力曲线和参数关系很大。
致谢
十分感谢张登科老师的仔细审阅和讨论。