1. 前言
我国的资源赋存特点是“富煤但油气不足”,因此煤炭地下气化也是一项具有中国特色的天然气开发技术。气化区处于高温高压环境,易引发顶板垮塌、围岩涌水、产出气逸散、地下水污染等安全问题。确保气化炉的密闭性对整个煤炭地下气化项目的顺利运行至关重要,因此需要对高温覆压下顶板围岩孔渗变化特征进行试验测试分析,其中对气化炉顶板泥岩渗透率的测试尤为重要。
国内外众多学者对不同温度或应力条件下岩石的气体渗透率进行过测试,其中,国外的研究起步很早,20世纪60年代,Somerton [1] 等就对温度作用下岩石的气体渗透率进行了研究,他们将砂岩岩心加热到400℃~800℃,发现岩样渗透率至少增加了50%。Randolph [2] 分析了有效应力和含水饱和度对岩石渗透率的影响及其相互作用关系,得出了气体渗透率随有效应力的增加而增大。国内在这方面的研究虽起步较晚,但发展迅速。在众多研究中都表明岩石的气体渗透率随着有效应力的增大而减小,整体上随温度的升高而增大 [3] - [11] 。刘均荣 [12] 等研究了粉砂岩的气体渗透率在较高温度下的变化,得到在100℃~300℃之间岩样渗透率随温度略微下降,300℃~500℃渗透率缓慢增加,500℃~800℃则迅速增加。对于岩石水渗的研究同样很多,除花岗岩外,规律与气渗基本一致 [13] - [19] 。刘德旺 [20] 研究了全应力应变下泥岩的水渗透率,得到泥岩的渗透率与应力状态关系密切,其渗透率的峰值往往滞后于应力应变峰值点。曾志蛟 [21] 等研究了泥岩和砂岩的水渗透率随围压变化特性,得出泥岩的渗透率随围压增加而下降的程度大于砂岩的,而砂岩的渗透率随围压减少而恢复的程度则远大于泥岩的。
从煤炭地下气化的角度来看,当前针对顶板泥岩渗透率和孔隙度的研究,要么测试的温度不够,要么未考虑全应力应变阶段,同样对同种岩石气渗和水渗特征的对比也不够充足。因此本文在三轴应力下对气化腔顶板泥岩的渗透率和孔隙度进行测试,分析温度和围压对泥岩气渗和水渗渗透率的影响规律,并对其规律进行拟合,便于后续的应用。
2. 试验测试方法
2.1. 气体渗透率测试方法
本研究使用了一套三轴应力下岩石孔隙度、渗透率测试系统,如图1所示。试验过程中,将气体钢瓶提供的氮气气源,经减压阀,以固定压力经气体流量计注入压力室中,通过无纸记录仪监测采集压力及流量的变化情况。
该试验系统各部件彼此独立并且便于拆装。试验过程中,油泵和压力室通过高压管道相互联系起来,接口通过快速插头,连接方便并且有效防止装置拆卸过程中漏油的现象。
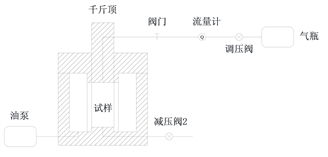
Figure 1. Diagram of rock porosity and permeability test system under triaxial stress
图1. 三轴应力下岩石孔隙度、渗透率测试系统及示意图
在气体渗透率的测试中,应力的加载方法:首先对试样加载一个初始的轴压(8或10 MPa),然后再进行围压的加载,当围压达到预设数值后停止围压加载;之后轴压采取分级加载,在泥岩的气体渗透率测试中加载梯度为5 MPa,然后进行一次渗透率测试,直至试样发生破坏其余试验参数如下:
① 试样制备及处理:获得不同温度(常温,200℃,400℃,600℃,800℃)热处理后的岩石标准试样。
② 气体渗透率测试:选取不同温度热处理后的试样,围压设置为8 MPa或10 MPa;
(2) 操作步骤:
① 热处理:将试样放入气氛炉中用石棉封住口部,再关闭炉门,加热前设置加热速率为10℃/min,加热温度依次为200℃,400℃,600℃,800℃ (损坏),恒温时间为两小时,加热结束后不要打开气氛炉,待其自动降温至50℃左右取出,用保鲜膜包裹,并贴上标签,加热路径曲线如图2所示。
② 渗透率测试前拆开包裹在试样上的保鲜膜,然用薄热缩膜对试样及上下透气/水板进行固定,然后使用绝缘胶带对固定后的试样进行缠绕(图3)防止实验过程中压力室(图4)的液压油进入试样,最后再用厚热缩膜对试样进行包裹,对试样的顶、底部位起到密封作用。
③ 将处理后的试样置于压力室中,用高强螺丝和密封垫片将压力室上部封盖,然后将压力室放置到试验机的平台上,插上提供围压的快插插头和带有减压阀或流量计的压力室出口快插插头(图5)。
④ 首先启动试验机,调整轴向加载速率为2 mm/min,加载目标值为5 MPa,待轴压达到目标值后打开柱塞泵,结合无纸记录仪上显示的围压数值,将围压调整至目标值(8或10 MPa)。
⑤ 打开气瓶,通过调压阀控制注气压力恒为2 MPa,打开压力室出口阀门,待流量计读数稳定后记下瞬态流量值,用于计算试样在该载荷下的渗透率。
⑥ 关闭压力室出口阀门,待出口压力稳定后,缓慢调整压力室入口压力至4 MPa,待出口压力稳定后(流量计的瞬态流量降为零),记录这一过程中流量计显示的累计流量,用于计算试样的孔隙度。
如此便进行了一轮的测试,第二轮测试前先提高轴压至下一目标值,重复⑤~⑥步,直至试样破坏,测试加载路径曲线如图6所示。
在拆卸过程中,需首先关闭气瓶停止注气,然后关闭柱塞泵卸掉围压,最后卸载轴压。另外需要注意的是,在泥岩渗透率测试时,由于试样强度较低,为防治初次加载轴压时试样发生破坏,需要在加载轴压的同时加载围压,但要保证围压时刻小于轴压的大小。

Figure 3. Pressure stabilizing valves at the outlet of gas tanks and chambers
图3. 控制气瓶出口、压力室出口气体压力的稳压阀实物图

Figure 4. Sample surface wrapping method
图4. 试样表面包裹方法
2.2. 孔隙度测试方法
在岩石孔隙度的测试中,需首先将试样按照测试气体渗透率的步骤,在初始轴压和围压下对试样进行一次渗透率测试。渗透率测试结束后随之进行孔隙度的测试,具体步骤如下:
① 关闭压力室出口阀门,待压力室出口压力稳定后(基本达到2 MPa与入口压力相等),将流量计表盘上的累计流量清零;
② 缓慢调节注入压力,使其缓慢增长至4 MPa (所有孔隙度测试中,均采用此数值,即保证压力变化量ΔP恒为2 MPa),调节过程中需要保证流量计的瞬态流量在量程内;
③ 稳定一段时间,待流量计显示的瞬态流量降为零后(出口压力达到4 MPa),记录下流量计的累计流量;
④ 调节压力室入口和出口的减压阀,使压力恢复到测试孔隙度之前的状态,进行下一次气体渗透率的测试。
重复①~④步骤,即可实现岩石的气体渗透率与孔隙度的同步测试,该测试方法不仅能够准确、快速的测得岩石试样的孔隙度,与气体渗透率同步测试还能节省试验所需的试样数目。试验过程中,发现了使用此方法测试孔隙度时,由于需要改变两次气体的渗透压力,会出现试样在强度峰值前发生破坏的情况,特别是试样的强度接近试验设置的测试轴压。
2.3. 水渗渗透率测试
高温覆压下顶板泥岩水渗透率测试系统(图7)是在气体渗透率测试系统的基础上改造而成,添加了高压注水装置采用气驱水注入的方法比传统的水泵注水控制起来更加方便与精密,另外,将压力室出口处的减压阀更换成了液体流量计。
同样使用气体钢瓶提供的氮气气源,经减压阀,以固定压力驱动储水罐中的水注入压力室中,通过无纸记录仪监测采集压力的变化情况。
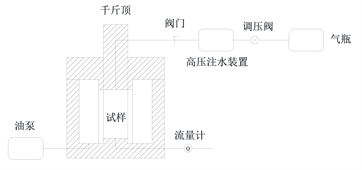
Figure 7. System of rock water permeability testing under triaxial stress and schematic diagram
图7. 三轴应力下岩石水渗透率测试系统及示意图
水渗透率测试选用的是稳态法,在测试过程中,应力的加载方法:首先对试样加载一个初始的轴压 (8或10 MPa),然后再进行围压的加载,当围压达到预设数值后停止围压加载;之后轴压采取分级加载,在泥岩的水渗透率测试时轴压每次加载数值为5 MPa,然后进行一次渗透率测试,直至试样发生破坏。
3. 测试结果及分析
3.1. 气体渗透率与温度和应力之间的关系
通过测试得到了加载过程中不同温度热处理后泥岩在各级载荷下的气体瞬态流量数值,结合试验原理,计算得到不同温度热处理后泥岩的渗透率数值。根据试验测试结果分别绘制泥岩的渗透率随温度、渗透率随轴压的曲线,如图8~11。
温度对泥岩渗透率的影响:初始条件下(10 MPa轴压、10 MPa围压),20℃~200℃时由于泥岩内部水分损失,导致孔隙体积上升,导致渗透率逐渐上升;200℃~600℃时高温导致岩石内部热破坏持续发生,生成的裂缝使得渗透率进一步增加;轴压对泥岩渗透率的影响:不同温度泥岩,保持围压8/10 MPa不变,轴压从10 MPa逐渐增加,在泥岩破坏前同样由于孔隙被压密,导致渗透率基本不变或略有降低;在岩石快发生破坏时由于裂隙迅速发育导致渗透率剧烈增加。轴压对泥岩渗透率的影响:其他条件相同时,增大轴压渗透率会下降,但根据试验结果可以看出,试样破坏前,围压对渗透率的影响较大,而试样破坏后,围压对渗透率的影响较小,可能是因为试样破坏前渗流通道主要为试样内部的孔隙,而试样破坏后主要的渗流通道变成了裂隙。
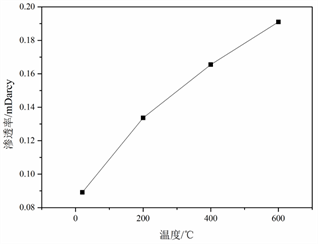
Figure 8. Variation curve of permeability with temperature
图8. 泥岩渗透率随温度的变化曲线(8 MPa)
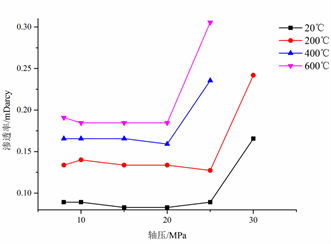
Figure 9. Variation curve of permeability with axial pressure
图9. 不同温度下泥岩渗透率随轴压变化曲线(8 MPa)
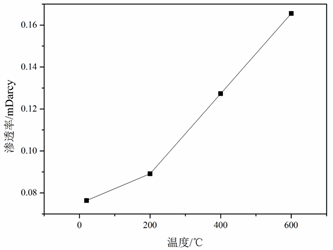
Figure 10. Variation curve of permeability with temperature
图10. 泥岩渗透率随温度的变化曲线(10 MPa)

Figure 11. Variation curve of permeability with axial pressure
图11. 不同温度下泥岩渗透率随轴压变化曲线(10 MPa)
3.2. 孔隙度与温度和应力之间的关系
在测试孔隙度时,由于中管道体积和试验环境中对应的其他参数的准确数值难以获得,因此试验时需利用已知孔隙体积的试样(图12和表1)进行测试获得标定曲线(图13)。测试试样时,将注气压力改变过程中的测得的气体累计流量代入标定曲线的拟合方程中获得试样的孔隙体积从而计算出试样的孔隙度。

Table 1. Calibration of sample size and pores volume
表1. 标定试样的尺寸及孔隙体积
根据试验获得的不同温度及轴向载荷下泥岩孔隙度测试数据,绘制出泥岩的孔隙度随温度和轴压的变化规律(图14和图15)。

Figure 14. Variation of mudstone porosity with temperature
图14. 泥岩孔隙度随温度变化规律
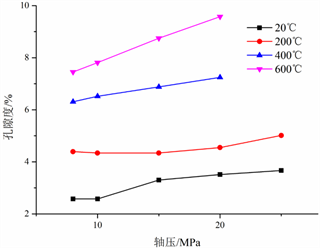
Figure 15. Variation of mudstone porosity with axial pressure
图15. 泥岩孔隙度随轴压变化规律
温度对泥岩孔隙度的影响:初始条件下(8 MPa轴压、8 MPa围压),同样因为水分的丢失,泥岩内部原本被水占据的孔隙体积被释放,导致泥岩孔隙度随温度的增加而增大;200℃~400℃时高温导致泥岩内部热破坏,孔隙、裂缝使得孔隙度迅速增加;600℃时热破坏导致的泥岩内部裂缝体积增大到一定程度,孔隙度增速降低;轴压对泥岩孔隙度的影响:不同温度泥岩,保持围压8 MPa不变,轴压从8 MPa逐渐增加,20℃~200℃时泥岩仍以脆性变形为主,轴压增大使得试样侧向体积膨胀,导致孔隙体积随轴压的增大而逐渐增加,因此孔隙度也基本随轴压的增加逐步增大;400℃~600℃时泥岩内部裂隙大量产生,孔隙度增速加快。
3.3. 水渗渗透率与温度和应力之间的关系
同样通过测试得到了加载过程中不同温度热处理后泥岩每级载荷下水的渗透率测试数据,根据图16到图19可以得到温度对泥岩渗透率的影响:初始条件下,20℃~200℃时由于热膨胀泥岩内部少量较大的孔隙被压密,导致渗透率有所下降;200℃~600℃时高温导致岩石内部热破坏,裂缝使得渗透率迅速增加。轴压对泥岩渗透率的影响:不同温度泥岩,保持围压不变,轴压逐渐增加,在破坏前由于没有产生较大的贯通裂隙,渗透率基本不变;在岩石快发生破坏时由于较大的贯通裂隙的产生,导致渗透率剧烈增加。围压从8 MPa增大到10 MPa,相同温度和轴压下泥岩的水渗渗透率略有降低。
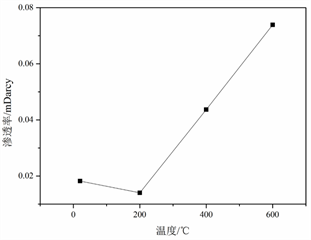
Figure 16. Variation of mudstone water permeability with temperature
图16. 泥岩水渗透率随温度变化规律(8 MPa)

Figure 17. Variation of mudstone water permeability with axial pressure
图17. 泥岩水渗透率随轴压变化规律(8 MPa)
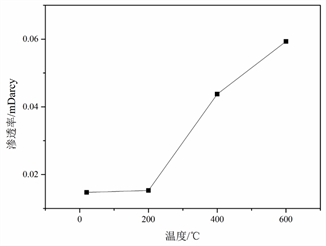
Figure 18. Variation of mudstone water permeability with temperature
图18. 泥岩水渗透率随温度变化规律(10 MPa)
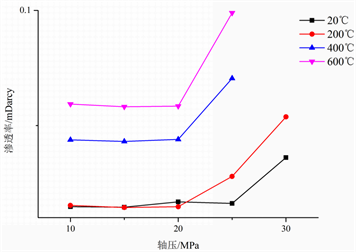
Figure 19. Variation of mudstone water permeability with axial pressure
图19. 泥岩水渗透率随轴压变化规律(10 MPa)
4. 高温热处理后泥岩应力–孔渗关系分析
为了对岩石的渗透率演化过程进行定量描述,国内外学者建立了大量的渗透率模型,其中一些模型具有较高的代表性,这些经典的模型成果在岩石渗透率模型的研究领域中发挥了重要作用。
Herron等 [22] 对单重孔隙砂岩油藏的研究发现,渗透率的对数与孔隙度有线性关系,
(1)
式中,k为渗透率,mD;φ为孔隙度,%;a和b为经验常数。式(16)没有考虑孔隙结构变化的影响,不能满足复杂条件下渗透率的精度要求。
对于均匀孔隙介质,Kozeny根据毛细管理论提出了一个公式,后来Carman对这个公式进行了证明,即Kozeny-Carman公式 [23] ,简称KC公式。它是一个理论公式,常用形式为:
(2)
式中,S0为比表面积,m2/m3;a为经验常数。在试验数据拟合中上式往往会产生一个常数项,由于比表面积不同的定义,式(2)还有其他形式。由于S0不能直接从测井资料获得,KC公式的应用受到了限制。
杨建等 [24] 根据毛细管束模型的渗透率表达式,应用分形模型计算了松散砂岩的渗透率
(3)
式中,τ为多孔介质孔隙迂曲度;λ为最小孔隙半径与最大孔隙半径之比;rmax为最大孔隙半径,μm;Dd为孔径分维数。
另外,还有基于平行板模型的裂隙介质渗透率模型将实际模型简化为由水平基质层和裂缝相互交替组成,但不考虑基岩的渗透率,裂缝渗透率可用式(4)计算
(4)
式中,φf为裂缝孔隙度,%;bf,为裂缝张开度,μm。
以上渗透率模型大多基于理论推导获得,均未考虑应力等其他因素的影响。李世平等 [25] 开展了岩石应力–应变–渗透率全过程试验研究,发现渗透率是轴向应力、应变的函数。采用Issac Newton提出的均差法,使一定数量的关键点和试验点上进行插值,得到拟合方程:
(5)
式中,ε为应变。
范学平等 [26] 应用岩心测试有效应力对渗透率影响的实验原理,在对实验数据进行统计分析的基础上,拟合出有效应力与渗透率的函数关系。应用毛细管渗流概念以及弹性厚壁简原理,研究了随着毛细管管壁内外压差变化时,毛细管内半径变化及其对毛细管渗流能力的影响,所得结论与实验结果一致。
(6)
式中:k为初始渗透率,10?3 μm2;σ为有效应力,MPa;a,b,c为拟合常数。
高旺来等 [27] 以初始有效覆压下的渗透率为参照,以实际压降路径范围下的渗透率变化比来评价地层压力变化对储层渗透率的影响,提出了下面的渗透率模型
(7)
式中,p0为初始压力,MPa;a为经验常数。
梁冰等 [28] 研究了温度对渗透率的影响规律并进行了理论分析,获得了温度–应力耦合的渗透率模型
(8)
式中,k0初始渗透率相关,mD;b与孔隙的压缩系数相关;σp为外部载荷,MPa;σ0为初始压力,MPa;aT为岩石的线膨胀系数,/℃;E为试样的弹性模量,MPa;μ为试样的泊松比;T为温度,℃。
渗透率建模的理论研究欠缺:一方面,关于渗流理论主要有毛细管束理论和Darcy定律。毛细管束理论将复杂的岩石对象抽象为等径或不等径的毛细管,然后采用Hagen-Poiseuille流动方程进行流动模拟,由于不能反映真实的岩石内部结构,因而据此建立的渗透率模型预测精度有限。Darcy定律是渗流力学中一个经典的公式,但应用时要注意Darcy定律也有局限性,当流动速度变大(比如岩石裂缝发育)或流体黏度变大时,将不满足Darcy定律,这时的流动是一种非Darcy流。另一方面没有提出通用的渗透率模型。岩石的岩性多样,内部结构复杂,影响渗透率的因素很多,许多学者提出了不同的渗透率模型,应用于具有不同特性的岩石,至今没有提出一个通用统一的渗透率模型。因此,一般通过分析渗透率的影响规律后,采用适当的渗透率模型,通过数据拟合获得模型中对应的参数,进一步应用于工程实践中。因此,这里首先分别对上节提到的部分渗透率模型进行数值拟合,分析各个模型的适应性,最终选择合适的渗透率模型应用于数值模拟中。
4.1. 岩石孔渗模型分析
(1) Herron提出的模型只能用来描述渗透率与孔隙度之间的关系,初始轴压下不同温度泥岩气体渗透率与孔隙度的拟合结果如图20,拟合方程如表2所示。从泥岩的拟合结果中可以看出,该模型也能描述泥岩气体渗透率与孔隙度之间的关系,但由于所有轴压下模型的拟合度下降较为明显,因此可以认为该模型用来描述泥岩气体渗透率与孔隙度之间关系时,轴压对模型的影响较为明显。
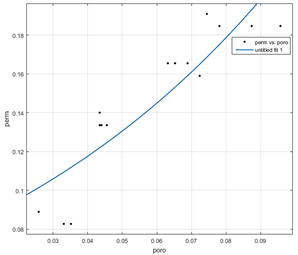
Figure 20. Relationship between gas permeability and porosity of mudstone at different temperatures
图20. 不同温度下泥岩气体渗透率与孔隙度的关系(左图为初始轴压,右图为所有的轴压)

Table 2. Fitting equations for gas permeability and porosity of mudstone at different temperatures
表2. 不同温度下泥岩气体渗透率与孔隙度的拟合方程
注:表中φ为孔隙度;f为对应的渗透率,mD。
(2) Kozeny-Carman公式虽然应用十分广泛,但同样只考虑了渗透率与孔隙度之间的关系,使用该模型对试验结果进行拟合,结果如图21,拟合方程如表3所示。拟合结果中可以看出,该模型对于所有轴压下泥岩的渗透率和孔隙度的关系拟合度不足0.8,因此在描述泥岩渗透率与孔隙度之间关系时,轴压对该模型的影响较为明显。
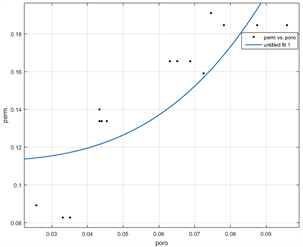
Figure 21. Relationship between gas permeability and porosity of mudstone at different temperatures
图21. 自不同温度下泥岩气体渗透率与孔隙度的关系(左图为初始轴压,右图为所有的轴压)

Table 3. Fitting equations for gas permeability and porosity of mudstone at different temperatures
表3. 不同温度下泥岩气体渗透率与孔隙度的拟合方程
注:表中φ为孔隙度;f为对应的渗透率,mD。
(3) 小结:单从拟合结果中看,上述两模型均可以用来描述泥岩渗透率与孔隙度之间的关系。但是在本试验中需要同时考虑应力和温度对泥岩渗透率和孔隙度之间的关系。因此需要尝试考虑更多因素的渗透率模型。
4.2. 应力–渗透率模型分析
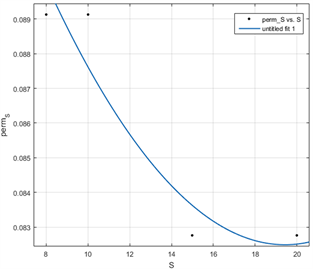
Figure 22. Relationship between gas permeability and axial pressure in mudstone at room temperature
图22. 常温下泥岩气体渗透率与轴压的关系
范学平和高旺来提出的模型中考虑了应力对渗透率的影响,因此这里只对常温不同轴压下的试验结果进行拟合,这里采用式(6)表示的模型进行拟合,结果如图22。根据拟合结果可以看出,虽然该模型对常温下泥岩渗透率与应力之间关系的描述较为准确。结合表4仔细观察后发现,泥岩的气体渗透率随轴压可以看作满足二次函数的关系。另外,该模型同样未考虑到温度对渗透率的影响,因此不能作为描述温度–应力作用下泥岩的渗透率变化规律。

Table 4. Fitting equations for gas permeability to axial pressure in mudstone at different temperatures
表4. 不同温度下泥岩气体渗透率与轴压的拟合方程
注:表中x为轴压,MPa;f为渗透率,mD;k0为各自的初始渗透率,mD。
4.3. 渗透率–温度–应力模型分析
(1) 梁冰提出的模型同时考虑了温度和应力的影响,使用该模型对泥岩气体渗透率试验数据进行拟合,结果如图23。从拟合结果中可以看出拟合曲面与试验结果的吻合程度较高,但是由于该模型中的参数均具有明确的物理意义,结合表5可以看出泥岩拟合方程中初始压力σ0对应的结果偏差过大,并且考虑到该模型只提供了渗透率的结果,在计算孔隙度时,还需要结合渗透率–孔隙度模型才能满足数值计算的需求。因此仍然不建议选用该渗透率模型。
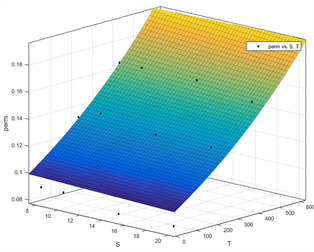
Figure 23. Fitting results for gas permeability of mudstone at different temperatures and axial pressures
图23. 不同温度和轴压下泥岩的气体渗透率拟合结果

Table 5. Fitting equations for gas permeability of sand and mudstone at different temperatures and axial pressures
表5. 不同温度和轴压下砂、泥岩气体渗透率拟合方程
注:表中x为轴压,MPa;y为温度,℃;f为渗透率,mD;k0为各自的初始渗透率,mD。
(2) 在气化腔气水运移规律数值模拟中,不仅需要通过温度和应力环境计算泥岩的渗透率,还需要获得泥岩对应的孔隙度,并且模型在形式上要尽量简单,便于编程应用,因此这里采用二元多项式对高温覆压下顶板泥岩孔隙度和渗透率试验数据分别进行拟合(见图24~26)。

Figure 24. Fitting surfaces for gas permeability of mudstone under temperature-stress coupling
图24. 温度–应力耦合下泥岩气体渗透率拟合曲面(围压左图8 MPa,右图10 MPa)

Figure 25. Fitting surface of mudstone porosity under temperature-stress coupling
图25. 温度–应力耦合下泥岩孔隙度拟合曲面

Figure 26. Fitting surfaces for water permeability of mudstone under temperature-stress coupling
图26. 温度–应力耦合下泥岩水渗透率拟合曲面(围压左图8 MPa,右图10 MPa)
从拟合结果来看,使用较低次幂的二元多项式已经完全可以用来拟合试验结果(表6),这些模型不仅可以用来研究岩石渗透率随温度、应力之间的关系,可以在数值软件中得到应用,比如在FLAC3D软件进行数值模拟时,可通过fish语言编程将这些试验规律应用于模型中去,能够更加真实的表征高温覆压下岩石的孔隙度、渗透率的变化特征。

Table 6. Fitting equations of pore-permeability models for sand and mudstone under temperature-stress coupling
表6. 温度–应力耦合下砂、泥岩孔渗模型拟合曲面方程及拟合优度
注:表中x为轴压,MPa;y为温度,℃;f为对应的结果(孔隙度,1;渗透率,mD)。
5. 结论
(1) 泥岩气渗渗透率随着温度的升高而升高,泥岩渗透率曲线升高的阈值为200℃左右;泥岩破坏前渗透率随轴压基本不变或略有降低,在岩石快发生破坏时渗透率剧烈增加。
(2) 泥岩孔隙度随温度整体随温度的升高而提高,基本没有阈值;泥岩在400℃~600℃时,由于试样产生了明显的纵向裂隙,孔隙度随轴压明显增大;泥岩孔隙度随轴向应力的增大而增大。
(3) 泥岩水渗透率与温度和轴压的关系与气测渗透率规律基本一致;泥岩三轴强度随围压的增大而增大、渗透率随围压的增加而减小;泥岩水渗得到的相对渗透率为气体渗透率的0.2到0.5倍。
(4) 利用二次多项式拟合高温覆压下顶板泥岩的气体渗透率、孔隙度和水渗透率效果更好,且便于后续应用在数值计算中。