1. 引言
随着地铁运营里程的不断增加,地铁运维中对地铁隧道和沿线设备的清洁作业逐渐开始采用专用的隧道清洗车来完成,以替代传统的人工清洗,极大的提高了清洗效率。隧道清洗车所需用的水通常采用水箱进行存储运输,水箱的容积决定了一次清洗作业的可持续时间。
隧道清洗车在进行清洗作业时速度一般为8 km/h,速度较慢,水的晃动较小,但在非作业时间时,运行速度较快,在加速、减速、紧急制动等情况下,储存在水箱内水的冲击和晃动情况非常严重,水箱所受载荷明显增加。因此,为满足载有水箱的隧道清洗车安全运行的要求,在载荷一定的情况下,为增加水的携带量,延长清洗作业的可持续时间,对水箱在不同工况下的载荷进行分析,并对其结构进行优化非常有必要。
RS Ganuga提出了一种用于液体晃动分析的流固耦合模型,通过改变罐体的激励幅值,比较了刚性挡板和柔性挡板在不同的晃动荷载作用下的力的响应 [1] 。黄文采用弹簧质量模型和流固耦合模型对大型储水罐进行相互验证计算 [2] 。汪孝凡基于流固耦合方法分析了水体与结构的相互作用,研究了外挂水箱结构的地震动响应以及水箱内水体振荡特性 [3] 。金斌采用流固耦合动态有限元方法,通过对典型行驶工况的分析探究了洒水车水箱内部浪涌对结构的影响 [4] 。李明华基于流固耦合的分析方法,采用RNGκ-ε的湍流模型,分析了管道的速度和压力分布 [5] 。李小珊研究了制动力对方形水罐的影响,并对比了几种防浪板对抑制水罐晃动的作用 [6] 。李保元利用VOF模型对水罐进行了加压数值模拟,确定了最佳的内腔体积与空气压缩比例 [7] 。刘小明采用双向流固耦合方法,对运动罐车在刹车过程中罐体内液体的晃动现象进行了数值分析,获得了罐体结构应力随时间的变化历程 [8] 。
本文通过对水箱不同储水量和不同运行速度等多种工况进行分析,确定储水量和运行速度对水箱冲击的影响规律。选择在最不利的工况条件,基于欧拉–欧拉多相流模型,采用单向流固耦合方法对水箱的受力和变形进行分析,根据分析结果在水箱内部增加了不同结构尺寸的隔板,在保证足够安全的情况下,降低水对水箱的冲击影响,减轻水箱的自重,为地铁隧道冲洗车水箱结构的设计及优化提供了更有效的参考。
2. 模型与计算方法
2.1. 整体结构模型
隧道清洗车所用水箱长约为6米,为不规则的椭圆形结构,最多可容纳水23 t。水箱材料均采用06Cr19Ni10不锈钢,这种材料具有良好的耐腐蚀性,耐热性、低温强度和机械特性 [9] 。水箱的侧壁和前后两个端面均采用薄壁结构,端面有平头和圆弧头两种常用结构,如图1所示。

 (a) 平头水箱 (b) 圆弧头水箱
(a) 平头水箱 (b) 圆弧头水箱
Figure 1. Two finite element models of water tanks
图1. 两种水箱端面结构示意图
水箱作为一个常压容器,端面为平头的水箱结构简单,加工难度低,可满足基本需要。端面为圆弧头的水箱加工难度有所增加,其抗压能力更强,也被经常使用。
2.2. 单向流固耦合
水箱内水的晃动属于较为典型的流固耦合问题,可视为空气–水–箱体三相介质的相互耦合,箱体作为固体域,刚性较好,变形量较小,采用单向流固耦合法求解较为理想。在计算时,将流体域的计算结果作为外部载荷通过流固耦合交界面传递给固体域,流体域和固体域的计算数据单向传递完成耦合计算。
在流体域的分析计算中,利用Workbench划分网格,选用fluent分析系统,使用VOF模型定义气液两相流,对箱内储水量和箱体运动速度及加速度进行设置,通过迭代求解直至流体域计算收敛,获得在不同工况下箱体内水的运动情况,以及不同工况下水对箱体的作用力。将这个作用力作为载荷通过流固耦合的方式加载到在固体域,完成固体域的计算,获得箱体的应变及应力情况,为箱体的优化设计提供数据支持。
2.3. 水箱结构模型
由于水箱体积较大,水管、气孔、安装基座等相关辅件较为复杂,因此在建立水箱结构模型时进行了简化,不考虑水箱相关辅件,仅分析水箱内水对箱体的影响。将简化后的平面水箱和圆弧水箱模型分别导入Workbench软件进行网格划分,平头水箱网格总节点数为148,457个,总单元数为75,265个,圆弧头箱网格总节点数为159,375个,总单元数为79,903个,划分网格如图2所示。

 (a) 平头水箱 (b) 圆弧头水箱
(a) 平头水箱 (b) 圆弧头水箱
Figure 2. The maximum impact pressure generated by water on the box
图2. 两种水箱有限元模型
2.4. 边界条件和工况
由于箱体的前后端面和侧面都受到水的冲击,选择所有的箱体内壁面为流固耦合面。固体域边界条件:对安装底座对应位置施加全约束。
当水箱随清洗车在轨道上运行过程中,在加减速和紧急制动时,都会产生一个加速度,从而引起水箱内水的晃动。
工况设置最高运行速度为16 m/s (57.6 km/h),制动加速度为−4 m/s²,水箱在4秒内停止运动,水箱内的储水量分别设置为50%、60%、80%、90%。
3. 结果分析
3.1. 箱体内水的运动对箱体的影响
(1) 水箱内气液瞬态分布
根据以上的计算方法和工况条件,对不同水位的箱体结构进行瞬态分析。图3为初始运行速度16 m/s,制动加速度−4 m/s²,80%储水量冲击下,水箱在不同时刻内部气液两相体积的瞬态分布情况,图中上部蓝色为空气的体积分布,下部红色为水的体积分布。
在相同工况条件下,平头水箱和圆弧头水箱气液两相瞬态分布基本相同,以圆弧头水箱为例。t = 0 s时,水箱内的水和空气界限分别,当开始制动时,水在惯性的作用下继续往前运动而产生涌动式冲击,在t = 0.6 s时,水对水箱的前端面产生最大的冲击力,之后水往后端面移动,前端面受到的冲击力逐渐减小,当t = 1.15 s时,前端面受到水的冲击力达到一个低值,之后又逐渐增大,但都不会超过t = 0.6 s时的峰值,当t = 4 s时,箱体停止移动,箱体前半部充满水,之后进入振荡衰减直至完全停止晃动。
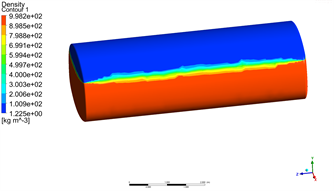
(a) t = 0 s
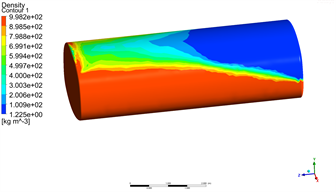
(b) t = 0.6 s
 (c) t = 1.15 s
(c) t = 1.15 s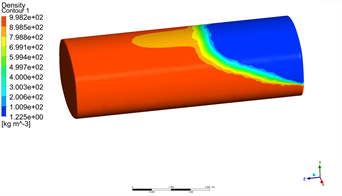 (d) t = 4 s
(d) t = 4 s
Figure 3. Transient distribution of gas-liquid two-phase flow in an 80% water storage tank (circular arc head water tank)
图3. 80%储水量箱体内气液两相瞬态分布(圆弧头水箱)
(2) 最大冲击压力
t = 0.6 s水对箱体的冲击力达到峰值,如图4所示。水的冲击力主要作用在水箱的前端面,从下至上呈阶梯状分布,最大的压力为3.76e4 Pa。平头水箱受到的最大冲击力分布与图4非常接近,最大的压力为3.68e4 Pa,也非常接近。在其他条件相同的情况下,水箱端面的结构形状对最大冲击压力基本不产生影响。
(3) 水箱前端面载荷分布
水箱前端面不同时间阶段受到的载荷分布如图5所示。水箱前端面在0.6 s时承受最大的冲击载荷,之后迅速下降进入调整,即一次制动只会对水箱前端面造成一次集中载荷。圆弧头水箱最大的载荷为124.2 KN。平头水箱受到的最大载荷为129.2 KN,也非常接近,在其他条件相同的情况下,水箱端面的结构形状对最大载荷影响非常小。

Figure 4. The maximum impact pressure generated by water on the box (80 % circular, arc head water tank)
图4. 水对箱体产生的最大冲击压力(80%储水量,圆弧头水箱)
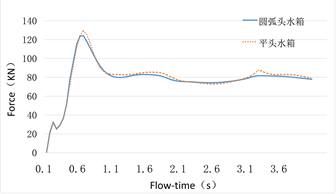
Figure 5. Load distribution at different time points on the front end face of the water tank
图5. 水箱前端面不同时间点载荷分布
(4) 水箱固体域分析
将上述流体域的计算结果通过单向流固耦合的方式传递给固体域,水箱壁厚为5 mm,可得到水箱在承受最大载荷时的应力和应变值。
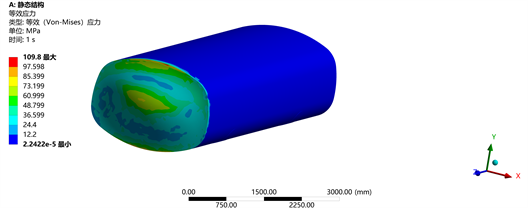 (a) 平头水箱
(a) 平头水箱 (b) 圆弧头水箱
(b) 圆弧头水箱
Figure 6. Stress cloud map of water tank under maximum load
图6. 水箱在承受最大载荷时应力云图
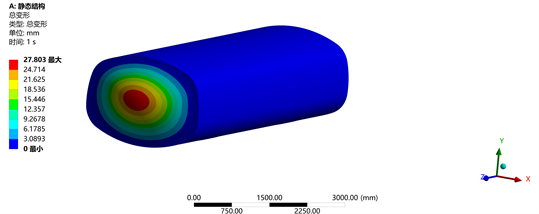 (a) 平头水箱
(a) 平头水箱 (b) 圆弧头水箱
(b) 圆弧头水箱
Figure 7. Cloud diagram of deformation of water tank under maximum load
图7. 水箱在承受最大载荷时形变云图
如图6和图7所示,应力最大值发生在水箱前端面下部,应变最大值发生在水箱前端面中间位置,在承受载荷非常接近的情况下,平头水箱产生的应力值109.8 MPa,形变量27.8 mm,圆弧头水箱产生的应力值120.7 MPa,形变量7.9 mm。这两种箱体结构的应力值都在材料的屈服极限(252 MPa)以内,但平头水箱的形变量太大,反复冲击容易对焊缝造成不利影响。本文后续分析均采用圆弧头水箱,其应力相对较大,形变量相对较小,水对水箱的冲击影响较大,现有水箱的结构需要进行优化。
3.2. 不同储水量对箱体的影响
在初始速度(16 m/s)和制动加速度(−4 m/s²)均不变的情况下,水箱内的储水量分别设置为50%、60%、80%、90%,对水箱前端面的载荷分布如图8所示。

Figure 8. Load distribution on the front end face of the box with different water storage capacities
图8. 不同储水量对箱体前端面的载荷分布
如图8所示,储水量90%时,最大冲击力在0.3 s时产生,随着储水量的减少,产生最大冲击力的时间也逐渐延后,储水量为50%时,最大冲击力在0.95 s时产生。储水量90%时,最大冲击力过后,箱体内的水波振荡衰减的最快,随着储水量的减少,水波振荡衰减所需的时间越长,当储水量为50%时,冲击力还会出现第二、第三次较为明显的峰值。

Table 1. Load distribution under different water storage capacities
表1. 不同储水量时载荷分布
如表1所示为不同储水量时对应的载荷分布情况,储水量从50%逐渐增大到80%的过程中,随着储水量的增加,最大载荷也随之增大,但当储水量为90%时,最大载荷反而比80%时小,这是因为当水箱接近装满时,没有足够的空间形成浪涌,前端面受到的载荷反而减小了。储水量处于80%左右时,水箱受到的冲击载荷最大,稳定性最差,后续分析均将储水量设置为80%。
4. 水箱结构优化设计
4.1. 单隔板水箱
水对水箱端面的冲击造成了较大的应力和应变,水箱内的水波振荡衰减速度较慢,为改善这一情况,在水箱中间位置设置一个隔板,以减少水的晃动和减小对水箱端面的冲击,隔板结构如图9所示。
如图9所示,单隔板将水箱平均分为2个互通的舱室,中间留有人孔,上下两端开口以连通两个舱室,单隔板的有效横断面积约为80%。
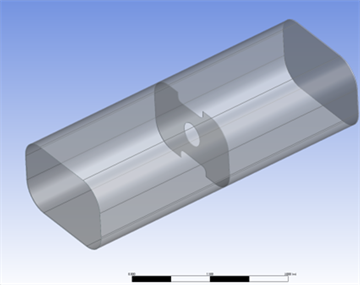
Figure 9. Schematic diagram of single partition water tank structure
图9. 单隔板水箱结构示意图
采用流固耦合的计算方法对流体域进行计算,保持初始速度(16 m/s)和制动加速度(−4 m/s²)不变,在储水量为80%的情况下,对设置有单隔板的水箱进行流体域仿真分析。水对水箱产生的最大冲击力如图10所示。
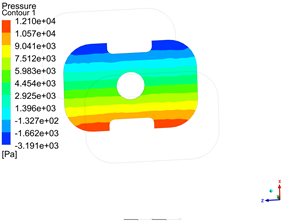
 (a) 箱体 (b) 隔板
(a) 箱体 (b) 隔板
Figure 10. Maximum impact pressure generated by water impact (single partition)
图10. 水冲击产生的最大冲击压力(单隔板)
由于有隔板的抑制,当发生紧急制动时,隔板阻断了部分水箱后部的水对前端面的冲击,前端面受到的冲击力由没有隔板时的3.76e4 Pa大幅度减小到1.71e4 Pa,隔板承受了部分冲击力。设定水箱从运动到制动结束总用时为4 s,分别对不同初速度(8~16 m/s)和不同制动加速度(−2~−4 m/s²)进行分析,载荷分布如图11和图12所示。
随着初始速度的提高,水箱前端面受到的最大冲击载荷也随之升高,最大冲击载荷发生的时间也随之提前。隔板所受冲击载荷会形成2次波峰,具体数值见表2。

Figure 11. Load distribution of water on the front end face of the water tank under different working conditions
图11. 不同工况下水对水箱前端面的载荷分布
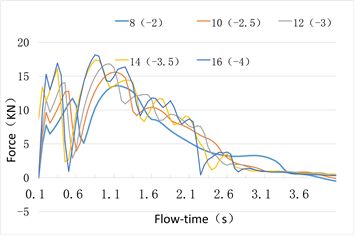
Figure 12. Load distribution of water on partitions under different working conditions
图12. 不同工况下水对隔板的载荷分布

Table 2. Load distribution of a single partition at different speeds
表2. 不同速度时单隔板载荷分布
随着初始速度的提高,水箱前端面受到的最大冲击载荷逐渐升高,发生最大载荷的时间也逐渐提前,初始运行速度对水箱所受冲击与水箱实际工作中的情况完全一致。隔板所受到的冲击载荷数值远小于前端面,所占比值随着速度的提高而逐渐减小,从29.8%逐渐降低到18%,速度越快,隔板为前端面承担了的载荷数值越高,但所占比值却呈下降趋势。在水箱中间增加隔板,可有效减小水箱前端面所受到的冲击载荷。
4.2. 双隔板水箱
为了进一步验证隔板对水箱冲击载荷的影响,在水箱内部设置双隔板,双隔板结构如图13所示。

 (a) 80% (b) 90%
(a) 80% (b) 90%
Figure 13. Schematic diagram of double partition water tank structure
图13. 双隔板水箱结构示意图
在长度为6米的水箱内部均匀设置2个隔板,隔板与端面之间的间隔为2米,2个隔板将水箱分为3个互通的舱室,中间留有人孔,上下两端开口,每个隔板的有效横断面积约为80%。当把中间的人孔去掉后,每个隔板的有效横断面积增大到90%左右。
采用流固耦合的计算方法对流体域进行计算,同样保持初始速度(16 m/s)和制动加速度(−4 m/s²)不变,在储水量为80%的情况下,对设置有双隔板的水箱进行仿真分析。水对水箱产生的最大冲击力如图14所示。

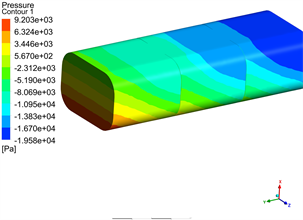 (a) 箱体 (b) 隔板
(a) 箱体 (b) 隔板
Figure 14. Maximum impact pressure generated by water impact (80%)
图14. 水冲击产生的最大冲击压力(80%)
由于有双隔板的抑制,当发生紧急制动时,双隔板部分阻断了水箱后两个部粉的水对前端面的冲击,前端面受到的冲击力由没有隔板时的3.76e4 Pa大幅度减小到9.2e3 Pa,双隔板承受了大部分冲击力。按文中3.1所设置的初始条件,对双隔板进行分析,结果如表3所示。

Table 3. Distribution of impact load on double baffles at different speeds
表3. 不同速度时双隔板冲击载荷分布
当有双隔板时,水箱前端面所受到的最大冲击载荷明显比单隔板时低,前隔板所受载荷明显大于单隔板时所受载荷,即前后两个隔板可为前端面分担更多的冲击载荷。双隔板水箱可更有效降低水对水箱的冲击,抑制水的晃动,提高水箱的安全性。
4.3. 水箱受力分析及结构优化
根据上述分析,得到了水箱的不同结构在不同工况下受到的载荷情况,如表4所示。

Table 4. Load distribution of water tanks with different structures under different working conditions
表4. 不同结构水箱在不同工况下的载荷分布
在相同的初始速度和制动加速度的情况下,设置有90%横断面积双隔板的水箱前端面受到的载荷最小,部分载荷被隔板承受并传递给了箱体,使箱体能均衡受力,这个结构最为合理。
对横断面积为90%的双隔板水箱进行结构受力分析,将上述流体域的计算结果通过单向流固耦合的方式传递给固体域,得到水箱在承受最大载荷时的应力和应变值如图15和图16所示。
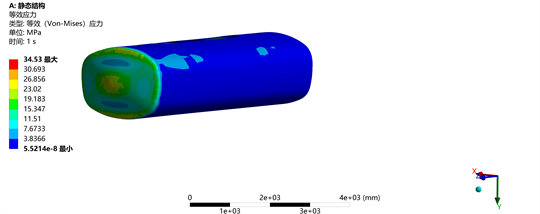
Figure 15. Stress cloud map of double partition (90%) water tank
图15. 双隔板(90%)水箱应力云图

Figure 16. Double partition (90%) water tank deformation cloud map
图16. 双隔板(90%)水箱形变云图
水箱壁厚为5 mm,水箱的应力和应变均发生在水箱前端,因为计算条件设置加速度为负值,水箱逐渐停止运动,水在惯性力的作用下对水箱前端产生冲击,如在加速启动的过程中,则后端面承受冲击载荷。最大应力为34.53 MPa,最大应变为4.68 mm,远低于材料的强度极限(252 MPa),安全系数很高,为了更有有效利用好隧道清洗车的承载能力,需要降低水箱自重,在保持清洗车总负载和尺寸不变的情况下,尽可能的多装水,以延长有效的清洗作业时长。
将水箱的前后端面、箱体、前后隔板分布设计为不同厚度,采用流固耦合的计算方法,计算结果如表5所示。

Table 5. Structural analysis of water tanks with different thicknesses
表5. 不同厚度水箱结构分析
当水箱的厚度均采用3 mm厚(5#水箱)的不锈钢时,其最大应力值为110.2 MPa,最大的应变值为10.5 mm,安全系数仍然较高,完成满足水箱这种常压容器的使用需求。
经过优化后的水箱自重由原来的1.79 t,降低到了1.21 t,在改变车辆承载能力和尺寸的情况下,可多装0.58 t水,可有效延长有效清洗作业时长。
5. 结论
本文基于有限元与单向流固耦合两种理论,以隧道清洗车的水箱为模型,利用有限元分析软件Ansys Workbench分别建立了水箱与流体的有限元模型。使用单向流固耦合方法,对平头、圆弧头两种端面结构的水箱在不同储水量、不同制动加速度的工况下施加冲击载荷进行计算,并将流体域的计算结果传递给固体域进行分析,得出以下结论:
(1) 通过单向流固耦合得到了不同端面结构在冲击载荷作用下的应力和应变值,结果表明圆弧头端面结构优于平头端面结构,储水量不同时,水箱受到的冲击载荷随储水量的增加而增大,当储水量超过80%时,由于没有浪涌形成的足够空间,冲击载荷反而减小了。
(2) 在水箱内部增设隔板可有效减小水的冲击力,对于容积为23 t的水箱,双隔板的设计可有限抑制水的晃动对水箱的冲击,当横断面积减小时,抑制效果更明显。
单向流固耦合的计算结构与实际情况相吻合,为地铁隧道冲洗车水箱结构的设计及优化提供了有效的参考。
参考文献