考虑多配送中心的外卖配送路径优化研究

Optimisation of Takeaway Delivery Routes Considering Multiple Distribution Centres

摘要: 外卖配送作为外卖平台运行中的重要部分，外卖配送的路径规划会直接影响外卖平台的经营效益和品牌影响力。本文以多个配送中心、多个商家和顾客组成的外卖配送系统为研究对象，综合考虑外卖配送运输成本、固定成本、出餐时间成本以及时间窗惩罚成本，加入单位车辆承载量上限和分段软时间窗约束等条件，以成本最小和顾客满意度最大为目标，构建了适合外卖专送模式下多配送中心的外卖配送路径优化的预优化模型和动态调整模型，并设计与之对应的混合遗传蚁群算法和遗传算法分别求解模型。最后通过算例分析和算法对比分析，验证本文构建模型的可行性和算法的有效性，为外卖行业管理决策提供参考。

Abstract: As an important part of takeaway delivery in the operation of takeaway platforms, the path planning of takeaway delivery will directly affect the operational efficiency and brand influence of takeaway platforms. This paper takes the takeaway delivery system composed of multiple distribution centres, multiple merchants and customers as the research object, comprehensively considers the transportation cost, fixed cost, meal delivery time cost and time window penalty cost of takeaway delivery, adds the upper limit of the carrying capacity of the unit vehicle and the soft time window constraints of the segments, and constructs a pre-optimization model and a dynamic adjustment model suitable for the takeaway delivery of multiple distribution centres under the mode of takeaway delivery, with the goal of minimizing the cost and maximizing the satisfaction of customers. A pre-optimisation model and a dynamic adjustment model for route optimisation are constructed, and the corresponding hybrid genetic ant colony algorithm and genetic algorithm are designed to solve the model respectively. Finally, the feasibility of the model and the effectiveness of the algorithm are verified through case analysis and algorithm comparison analysis, which provide reference for the management decision of takeaway industry.

1. 引言

外卖行业是近年来快速崛起的新兴行业，其发展势头迅猛，被誉为“互联网 + 餐饮”的典型代表。根据市场研究机构的数据显示，预计到2023年年底，中国外卖市场规模将达到12,449亿元，年均增长率增加至17.7%。这一数据表明，外卖行业正在成为餐饮行业的新引擎，对经济增长具有重要的促进作用。

传统的专送外卖配送方式通常是由骑手根据单个订单的需求完成配送任务，然而，单个骑手的能力和效率是有限的。当订单量大、配送距离远、送餐时间窗短时，这种方式往往无法满足快速、高效的配送需求。因此，如何合理分配骑手资源，规划优化送餐路径成为了外卖行业亟需解决的重要问题。

目前针对外卖配送路径优化的研究较为丰富。国外有关学者的研究如下：Zuhal Kartal等(2017)提出了单个分配p-hub取送货问题，最小化在中转和在网络中配送的成本，基于多次启动模拟退火和蚁群系统的两个启发式方法来解决这些问题 [1] 。Siwaporn Kunnapapdeelert，等(2018)介绍了四种解决多仓库车辆路径问题的新的改进的差分演化算法，其中两种改进的差分演化算法基于子群划分思想以解决GVRP-MDMPDR问题 [2] 。Yong Wang等(2019)探讨了如何通过均衡匹配不均匀分布的需求和供应量，并制定和解决了一种基于时间窗口的协同提货和交付问题 [3] 。Napoleão Nepomuceno等(2019)提出了一种使用最近邻策略的快速随机化算法来解决车辆配送问题 [4] 。Yong Shi等(2020)提出了一种有效的基于学习的两阶段算法来解决VRPSPDTW问题 [5] 。Elena S. Pavlova等(2021)考虑提货和交货、时间窗口和运输工人的分配问题，采用鲁棒优化方法改善了决策并促进员工合作，从而降低了总运输成本 [6] 。Zhou等(2022)提出了一种用于具有时间窗和同时提货和交货的两层车辆路径问题(2E-VRPTWSPD)的禁忌搜索算法，这是两层车辆路径问题的一个新变体 [7] 。Lu Yichen等(2022)将卡车和无人机合作配送模型应用于物流配送中，并提出了一个多目标交付车辆联合无人机的路径问题 [8] 。Guo Qinge等(2023)为了有效地为物流公司优化运营，介绍了考虑总收集货物数量的同时取送货车辆路径问题，开发了一个双目标车辆路径模型，基于ε约束方法，设计了一个多项式时间逼近算法来解决这个问题 [9] 。Ren Teng等(2023)基于配送低碳环保、需求分割和取送结合的特点，建立了以最小化总成本为目标的数学模型，并设计了一种改进的蚁群优化(ACO)算法来解决这个模型 [10] 。

国内有关学者的研究如下：熊浩等(2022)研究派单模式下动态实时配送优化问题，根据计算规则、执行规则等划分派单场景，并运用优化算法进行优化决策，并以实际外卖平台案例进行仿真验证 [11] 。杨浩雄等(2022)认为消费者进行外卖订购时，可能会出现一单多品的情况，所以其将一单多品这一因素考虑在内，并利用遗传算法求解订单配送问题，实验结果证实了模型有效性 [12] 。夏忠宇(2023)认为传统外卖配送方式效率过低，成本过高，所以其研究以降低成本和提高顾客满意度为目标的外卖路径优化问题，并基于遗传算法进行求解 [13] 。高椿林等(2023)将员工满意度这一因素考虑在内，并构建了考虑员工满意度的数学模型，然后提出符合研究问题的两阶段初始解构造法，并对自适应大邻域搜索算法进行改进以求解最优配送路径 [14] 。吴廷映等(2023)将传统运输陆地卡车方式和现代运输空中无人机运输相结合，提出了一种卡车和无人机相结合运输的取送车辆路径问题 [15] 。李熠胥等(2023)将保护环境绿色碳排放因素引入取送车辆路径问题中来，以碳排放成本最小为优化目标构建数学模型 [16] 。周雅兰等(2023)利用深度学习算法解决带时间窗和车辆容辆限制的车辆取送货路径优化问题，主要运用Memetic算法求解，并构建编码与解码相结合的深度学习模型完成基本操作 [17] 。

综上所述，相关文献主要从影响外卖配送的相关因素以及求解算法优化两个方面进行研究。上述文献中影响外卖配送的相关因素主要有骑手的分配、无人机运作、一单多品等，但是上述研究都是基于某一配送中心进行的模型构建，相关文献中对于多配送中心的外卖配送问题研究较少，而在有关美团或饿了么等外卖平台下，某一城区会设立多个配送站点进行城区内外卖的配送，所以针对多配送中心的外卖配送问题研究还是有必要的。所以本文考虑到外卖配送中心数量这个因素，在传统专送外卖配送研究的基础上，构建外卖专送模式下考虑多配送中心的外卖配送路径优化预优化模型和动态调整模型，综合考虑车辆派送的固定成本、运输成本、等待商家出餐时间成本以及分段超时惩罚成本，并且通过设计相关混合遗传蚁群算法和遗传算法进行求解，目的是降低成本，提高配送效率和客户满意度。

2. 问题描述与建模

2.1. 问题描述

本文的主要研究对象为多个配送中心，多个取餐点(商家)和多个送餐点(客户)，每个配送中心有固定数量的配送员(骑手)，客户在商家经营时间范围内点外卖，外卖配送平台派单给处于各个配送中心的配送员(骑手)，配送员的驾驶车辆为外卖平台统一配置的电动车，配送员接单后统一从配送中心出发，对于同一订单采取先取后送的原则进行配送，配送途中可以去其他商家或者客户处取餐或者送餐，为便于外卖平台统一管理配送车辆，待所有配送订单完成后，配送员需返回其所在的原配送中心，形成一条闭环配送路线，至此完成所有配送任务。具体运送情况见图1和图2。

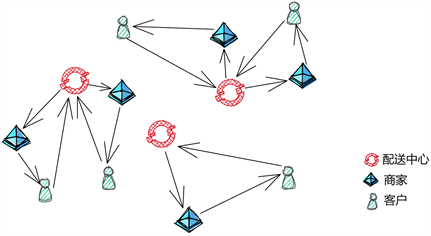
Figure 1. Multiple distribution centre model

图1. 多配送中心模式

Figure 2. Dynamic adjustment path diagram

图2. 动态调整路径图

2.2. 模型假设

H1：配送中心的车辆数量固定且满足订单需求量。

H2：各个配送中心的配送车辆属于相同规格，最大行驶里程、最大货物承载量、运行功率电压等都相同且满足配送需求。

H3：不考虑由天气状况、交通拥堵、事故或者道路维修等原因造成的影响。

H4：不考虑例如单份外卖重量直接超过车辆承载量的特殊订单。

H5：已知所有配送中心、客户、商家的位置，每位骑手配送路径完成后的终点位置为车辆出发时的原配送中心，即执行外卖配送任务的车辆需形成一条闭环路线。

H6：客户的时间窗已知，且为软时间窗，当配送车辆到达客户处时不在时间窗范围内，即早到或者晚到时，客户不拒绝服务，但是晚到情况下，会根据晚到时长进行分段超时惩罚。

2.3. 参数设置

本文根据研究内容构建数学模型的详细参数见表1~3：

Table 1. Description of set parameters

表1. 集合参数说明

Table 2. Description of general parameters

表2. 常规参数说明

Table 3. Description of decision variables parameters

表3. 决策变量参数说明

2.4. 模型构建

首先，考虑多配送中心的外卖配送路径优化问题模型以最小化的配送成本和最大化客户满意度为目标，具体考虑如下目标：

1) 车辆行驶路径距离成本

本文用c₁表示配送车辆行驶过程中由于耗电能产生的单位距离成本，用Z₁表示整个多配送中心下派出车辆所产生路径的总距离成本，Z₁表示如下：

$Z_1=c_1{\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{j\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{p\in P}{\sum }{d}_{ij}{x}_{ij}^{pk}}}}}$ (1)

2) 车辆取餐等待时间成本

每个商家出餐时间可能都不同，所以本文根据外卖配送实际情况设置的出餐时间是5~10分钟，用t_c表示，用c₂表示车辆取餐单位等待时间成本，车辆取餐等待时间成本用Z₂表示，具体公式如下：

$Z_2=c_{2}n{t}_c$ (2)

3) 超时分段惩罚成本

Z₃表示为超时惩罚成本， $t_{jk}^{pm}$ 表示为配送中心p出发的车辆k遍历m个点，抵达客户j的时间， ${t^{\prime }}_j$ 表示为配送车辆将订单送达的最晚时间，见图3，当订单送达时间处在 $\left[0,{t^{\prime }}_j\right]$ 之内时，不产生任何惩罚成本，当订单送达时间处在 $\left({t^{\prime }}_j,t\right]$ 时，会产生c₃的单位时间惩罚成本，当订单送达时间在 $\left(t,\infty \right)$ 时，将会产生 $c_{3}t$ 的时间成本以及额外超过t部分的 ${c^{\prime }}_3$ 的单位时间成本，因此，配送车辆的超时惩罚成本Z₃的公式如式(3)所示。

$Z_3=\{\begin{array}{l}{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{j\in N}{\sum }{c}_3\max \left(t_{jk}^{pm}-{t^{\prime }}_j,0\right),t_{jk}^{pm}<{t^{\prime }}_j+t}}}\\ {\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{j\in N}{\sum }\left\{c_{3}t+{c^{\prime }}_3\left(t_{jk}^{pm}-{t^{\prime }}_j-t\right)\right\},t_{jk}^{pm}\ge {t^{\prime }}_j+t}}}\end{array}$ (3)

Figure 3. Time window schematic

图3. 时间窗示意图

4) 外卖配送车辆固定成本

外卖配送车辆固定成本是指外卖平台设置配送中心，从配送中心派遣的外卖配送车辆所产生的一定费用，主要包括车辆的磨损成本、维修费用等成本，外卖配送车辆固定成本仅与派遣的车辆数量有关，派遣车辆越多则产生的固定派遣成本越高，并用Z₄表示，具体公式如式(4)所示：

$Z_4={\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{c}_4{G}_i^{pk}}}}$ (4)

综上，预优化阶段数学模型表示为：

$\min C=Z_1+Z_2+Z_3+Z_4$ (5)

$\min C=\{\begin{array}{l}{c}_1{\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{j\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{p\in P}{\sum }{d}_{ij}{x}_{ij}^{pk}+c_{2}n{t}_c}}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{j\in N}{\sum }{c}_3\max \left(t_{ij}^{pm}-{t^{\prime }}_j,0\right)}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{c}_4{G}_i^{pk},t_{jk}^{pm}<{t^{\prime }}_j+t}}}\\ c_1{\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{j\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{p\in P}{\sum }{d}_{ij}{x}_{ij}^{pk}+c_{2}n{t}_c}}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{j\in N}{\sum }\left\{c_{3}t+{c^{\prime }}_3\left(t_{jk}^{pm}-{t^{\prime }}_j-t\right)\right\}}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{c}_4{G}_i^{pk},t_{jk}^{pm}\ge {t^{\prime }}_j+t}}}\end{array}$ (6)

S. T.

$q_{ik}^{pm}=\{\begin{array}{l}{q}_{jk}^{p\left(m-1\right)}+E_{i^{\prime }},\forall i,j\in A,k\in K,i^{\prime }\in M,p\in P\\ q_{jk}^{p\left(m-1\right)}-F_{j^{\prime }},\forall i,j\in A,k\in K,j^{\prime }\in N,p\in P\end{array}$ (7)

$q_{ik}^{pm}+E_{i^{\prime }}\le Q^k,i\in A,i^{\prime }\in M,j^{\prime }\in N,k\in K,p\in P$ (8)

$q_{ik}^{pm}-F_{j^{\prime }}\le Q^k,i\in A,i^{\prime }\in M,j^{\prime }\in N,k\in K,p\in P$ (9)

${\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{j\in A}{\sum }{x}_{ij}^{pk}{E}_{i^{\prime }}}}={\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{j\in A}{\sum }{x}_{ij}^{pk}{F}_{j^{\prime }}}},k\in K,p\in P$ (10)

$l_{ik}^{pm}=t_{ik}^{pm}+t_c,i\in A,k\in K,p\in P$ (11)

$\begin{array}{l}{t}_{jk}^{pm}=t_{jk}^{p\left(m-1\right)}+t_c+d_{ij}/v^k\\ i,j\in A,k\in K,p\in P,i\ne j\end{array}$ (12)

$\begin{array}{l}{x}_{ij}^{pk}\left(t_{ik}^{pm}+t_c+d_{ij}/v^k-t_{jk}^{pm}\right)\le 0\\ i,j\in A,k\in K,p\in P,i\ne j\end{array}$ (13)

${\displaystyle \underset{i\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{x}_{ij}^{pk}=1\text{,}j\in M,p\in P}}$ (14)

${\displaystyle \underset{j\in A}{\sum }{\displaystyle \underset{k\in K}{\sum }{x}_{ij}^{pk}=1,i\in N,p\in P}}$ (15)

${\displaystyle \underset{k\in K}{\sum }{G}_i^{pk}=1,i\in M,p\in P}$ (16)

$F_{ij}{G}_i^{pk}={\displaystyle \underset{i\in A}{\sum }{x}_{ij}^{pk},i\in M,J\in N,k\in K,p\in P}$ (17)

在考虑多配送中心外卖路径优化数学模型中，式(6)表示预优化模型的目标函数，以配送总成本和客户满意度最大为目标，具体包括配送车辆行驶距离成本、等待出餐时间成本、超时惩罚成本以及配送车辆固定成本。在上述约束条件中，式(7)~式(10)为车辆载重相关约束，式(7)表示从配送中心p出发的车辆k在当前所处节点的载货量；式(8)和式(9)表示配送车辆在任意节点处的载货量不能超过其车辆本身的最大承载量；式(10)表示配送车辆取送货总量相同；式(11)~式(13)为相关时间约束条件，式(11)表示配送车辆离开商家的时间；式(12)表示配送车辆抵达顾客处的时间；式(13)表示配送车辆进行配送时要满足先取后送；式(14)~式(17)表示其他相关约束：式(14)和式(15)表示任意商家或者顾客节点只能由某一配送中心的某一车辆经过一次；式(16)表示一笔订单由任意配送中心中的某一车辆进行配送；式(17)表示一笔订单中的商家和顾客是一一对应的。

本阶段以上述预优化模型得出的优化路径为基础，根据新生订单时刻配送车辆所处位置信息以及待配送订单信息，重新规划路径，建立的动态调整模型如下：

$\min C=\{\begin{array}{l}{c}_1{\displaystyle \underset{i\in A^{\prime }}{\sum }{\displaystyle \underset{j\in A^{\prime }}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{p\in P}{\sum }{d}_{ij}{x}_{ij}^{pk}+c_{2}n{t}_c}}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{j\in N^{″}}{\sum }{c}_3\max \left(t_{ij}^{pm}-{t^{\prime }}_j,0\right)}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{i\in A\text{'}}{\sum }{\displaystyle \underset{k\in K}{\sum }{c}_4{G}_i^{pk}\text{,}{t}_{jk}^{pm}<{t^{\prime }}_j+t}}}\\ c_1{\displaystyle \underset{i\in A^{\prime }}{\sum }{\displaystyle \underset{j\in A^{\prime }}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{p\in P}{\sum }{d}_{ij}{x}_{ij}^{pk}+c_{2}n{t}_c}}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{j\in N^{″}}{\sum }\left\{c_{3}t+{c^{\prime }}_3\left(t_{jk}^{pm}-{t^{\prime }}_j-t\right)\right\}}}}+{\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{i\in A\text{'}}{\sum }{\displaystyle \underset{k\in K}{\sum }{c}_4{G}_i^{pk}\text{,}{t}_{jk}^{pm}\ge {t^{\prime }}_j+t}}}\end{array}$ (18)

S. T.

$\begin{array}{l}{\displaystyle \underset{k\in K}{\sum }{G}_i^{pk}}={\displaystyle \underset{k\in K}{\sum }{G}_i^{pk}=1}\\ p\in P,i\in M,j\in N\end{array}$ (19)

${\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{G}_i^{pk}=\left|N_k\right|\text{,}i\in N}}$ (20)

$\begin{array}{l}{t}_{jk}^{pm}\ge t_{ik}^{pm}+\frac{d_{ij}}{V^k}\\ k\in K,\forall i,j\in Y,p\in P\end{array}$ (21)

${\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K_x}{\sum }{G}_i^{pk}=\left|K_x\right|\text{,}i\in Y_3}}$ (22)

${\displaystyle \underset{p\in P}{\sum }{\displaystyle \underset{k\in K}{\sum }{G}_i^{pk}=1\text{,}i\in H}}$ (23)

$\begin{array}{l}{t}_{ik}^{pm}+t_c+\frac{d_{ij}}{V^k}\le t_{ij}^{pm}\\ \forall i\in Y,k\in K,p\in P\end{array}$ (24)

$\begin{array}{l}{\displaystyle \underset{k\in K}{\sum }{\displaystyle \underset{i\in R_k}{\sum }{G}_i^{pk}}={\displaystyle \underset{k\in K}{\sum }{G}_j^{pk}}=1}\\ p\in P,i\in M,j\in N\end{array}$ (25)

式(18)为动态优化模型目标函数；式(19)表示新增订单的取送货点只能由某一配送车辆进行配送；式(20)表示上阶段已派配送车辆在动态优化阶段的所配送订单必须包含上阶段已取未送以及未取未送的订单；式(21)表示配送车辆配送订单的相关时间约束；式(22)表示新增配送车辆以其所属配送中心为起点；式(23)表示上阶段已派配送车辆从接收新订单时刻的位置为起点；式(24)表示动态阶段订单先取后送的约束；式(25)表示动态阶段的订单都得以配送。

3. 算法设计

本文预优化模型采用的算法为混合遗传蚁群算法，其是一种结合了遗传算法和蚁群算法的优化算法。以上述预优化模型算法得出的最优解作为基础，综合考虑外卖订单动态需求，继续采用动态调整模型算法进行求解，此处的动态调整模型算法设计主要采用设计后的遗传算法。

3.1. 算法步骤

1) 混合遗传蚁群算法步骤

首先，获取初始蚁群并进行修复 → 精英选择 → 种群适应度 → 更新信息素矩阵 → 进化操作 → 精英策略 → 判断是否满足终止条件，若满足则输出结果，不满足则重复以上步骤。

2) 遗传算法步骤：初始化种群 → 计算适应度 → 进化操作 → 精英策略 → 判断是否满足终止条件，若满足则输出结果，不满足则重复以上步骤。

下面对以上算法设计部分进行详细阐述：

3.2. 算法设计

1) 染色体编码

本文主要通过自然数编码形式进行编码，以一个具有N个需求点，M个供应点，每个供应点最多可派遣K辆车的问题为例进行编码的解释说明。如图4所示，一个个体所具有的基因个数为N + M * K，其中编号小于等于N的基因代表需求点，大于N的基因代表不同供应点派遣的车辆。

Figure 4. Individual coding scheme

图4. 个体编码方案

2) 初始化种群

首先初始化混合遗传蚁群算法中的蚁群算法所需参数，获得初始种群，对所有位置进行编码；然后构造解空间，将蚂蚁随机放置在任意坐标点，根据路径上的信息素量和启发信息等因素确定蚂蚁转移概率，运用轮盘赌选择策略选择蚂蚁下一个行进地点，在此过程中不断更新禁忌表。上述蚂蚁转移概率是按照式(26)来进行计算的：

$P_{ij}^k\left(t\right)=\{\begin{array}{l}\frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{\alpha }\times {\left[{\eta }_{ij}\left(t\right)\right]}^{\beta }}{{\displaystyle \underset{k\in allowe{d}_k}{\sum }{\left[{\tau }_{ik}\left(t\right)\right]}^{\alpha }\times {\left[{\eta }_{ik}\left(t\right)\right]}^{\beta }}}\text{if}j\in allowe{d}_k\\ 0\text{others}\end{array}$ (26)

其中i，j分别为起点和终点； ${\tau }_{ij}\left(t\right)$ 代表t时间时由i到j的信息素浓度， ${\eta }_{ij}$ 为能见度，具体表示为 ${\eta }_{ij}=1/d_{ij}$ ，即i到j距离的倒数； $allowe{d}_k$ 为蚂蚁还未访问过的节点集合， $\alpha$ 和 $\beta$ 分别为信息素重要程度参数和启发式因子重要程度参数。

3) 修复方案设计

在本文的外卖配送方案中由于采取的是外卖平台专送模式，所以每辆车的起点应为“车辆基因”，若不满足情况，那么从左往右遍历找出第一个“车辆基因”，并将首个基因与该“车辆基因”置换位置。如图5所示：

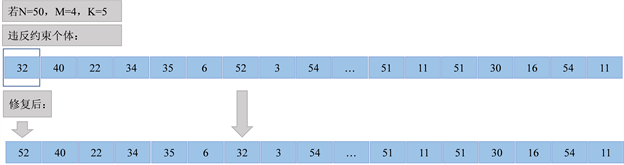
Figure 5. Distribution center rehabilitation program

图5. 配送中心修复方案

其次是车辆载重惩罚因子操作。由于每辆车均有其最大配送量，随机置乱所产生的个体解码出的车辆路径有可能存在单条路径的需求总量超过车辆的最大载货量的情况。故惩罚因子设定值要尽可能的大，本文实验中设定的值为10¹⁰。

第三是先取后送修复。第一步，由于配送中心首位修复后的种群中每个个体所涉及的染色体片段首位都为配送中心，而配送的商家和客户需要满足一一对应的关系，所以每段染色体中除第一个染色体外，后面应为偶数个染色体，若不满足偶数个，则将染色体片段最后面的染色体放入个体的下一段染色体片段中，直到个体中各个染色体片段满足上述要求；第二步，将第一步修复好的个体中商家和客户分别按其在个体中的顺序分成两组；第三步，根据个体染色体片段生成包含a，b的个体序列，a代表商家，b代表客户，从左至右生成a的个数要大于等于b的个数，若小于b的个数，则将此处a的位置换为b，直到满足商家数为止，后面若再出现a，则换为b；第四步，个体序列生成后，将第二步商家组合中的商家编号依次放在a所在的位置，然后在客户组中找到此商家对应的客户编号依次放入b所在的位置；第五步，若序列中某一对商家和客户取送关系不满足商家在前顾客在后，则直接调换二者位置。以此类推依次修复种群内所有个体。

4) 适应度函数

本研究目标函数为极小化问题，在设置适应度函数时需其取倒数，由此计算每个染色体适应度并排序。

5) 精英策略

混合遗传蚁群算法在种群进化过程中实施了两次精英策略，前一次精英选择策略是初始种群生成后的迭代过程中把父代种群中最优秀的个体挑选出直接复制进下一代中，后一次的精英策略是在进化算子操作后，在父代和子代种群中选择前50%适应度值靠前的个体生成新种群。

6) 更新信息素

以下公式表示信息素更新的过程，其中k为蚂蚁数量， ${\tau }_{ij}\left(t+1\right)$ 表示当前的信息素浓度。 $\rho$ 是信息素的蒸发系数，用于控制信息素的挥发速度。 $1-\rho$ 表示信息素在每次更新后的保留比例。 $\Delta {\tau }_{ij}$ 是信息素增量，表示在当前迭代中蚂蚁留下的信息素增量，Q为蚂蚁释放的总信息素， $pop{f}_k$ 为蚂蚁k形成路径的适应度值。

${\tau }_{ij}\left(t+1\right)=\left(1-\rho \right){\tau }_{ij}\left(t\right)+\Delta {\tau }_{ij}$ (27)

$\Delta {\tau }_{ij}^k=\frac{Q}{pop{f}_k}$ (28)

$\Delta {\tau }_{ij}={\displaystyle \underset{k=1}{\overset{k}{\sum }}\Delta {\tau }_{ij}^k}$ (29)

7) 选择操作

求解预优化模型和动态调整模型中的选择策略采用的是锦标赛选择算子，在本研究中竞赛规模设定为2，具体见图6。

Figure 6. Tournament selection

图6. 锦标赛选择

8) 交叉操作

在预优化算法中的交叉操作举例说明如图7所示，从种群中任意再选择一个个体，找出G1 = 34在该个体中，上一个位置的点，如上一个点G3 = 3，则回到原来的个体，将点35到3之间倒置。

9) 变异操作

本文预优化阶段变异所用策略是将两个基因位r0，r1之间整体倒置，如图8所示，所以新策略的扰动只会改变2处的距离，分别是r0位左距离和r1位右距离；动态调整阶段的变异操作分为两段，第一段是组合编码的变异操作，与预优化阶段算法的变异操作相同，第二段是实数部分的变异操作，在此部分使用的是传统实数变异，即给数值加上或者减去一个值，这个数值称为步长。

Figure 7. Cross operation

图7. 交叉操作

Figure 8. Variant operation

图8. 变异操作

4. 算例求解与分析

4.1. 算例描述

选取无锡市M外卖平台在2023年11月13日11:00~11:05五分钟内的56笔订单数据，作为预优化模型的运行数据，将动态调度时间运行至11:30，共动态调整五个时间段。预优化阶段配送中心和需求点坐标如图9所示：

Figure 9. Location map

图9. 地点位置图

4.2. 参数设置

1) 模型参数设置

数学模型相关参数取值见表4：

Table 4. Model parameter settings

表4. 模型参数设置

2) 算法参数设置

算法具体参数取值详见表5：

Table 5. Parameters involved in the algorithm

表5. 算法中涉及的参数

4.3. 算例求解

将商家、客户以及配送中心的相关数据导入算法程序，首先预优化阶段算法迭代图见图10，预优化阶段结果见图11。

接着根据上述预优化模型得出的优化解，继续运用动态调整模型进行动态求解，设定5分钟为一个时间段进行动态调度，得出以下动态调整后的路径规划结果，见图12：

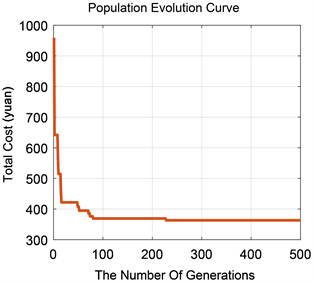
Figure 10. Iterative diagram of the algorithm for the pre-optimisation phase

图10. 预优化阶段算法迭代图

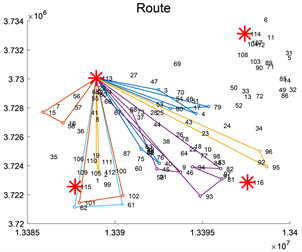
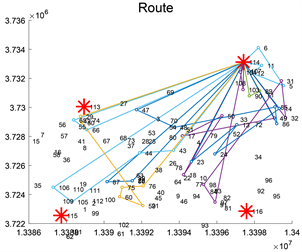
Figure 11. Path planning diagram for the pre-optimisation phase

图11. 预优化阶段路径规划图

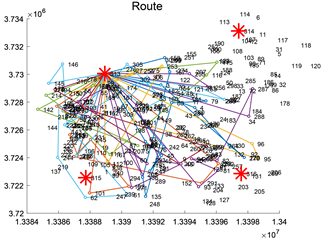
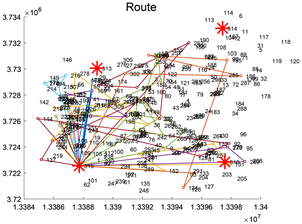
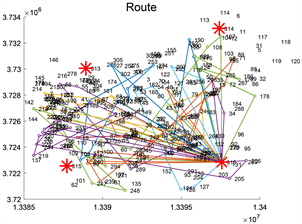
Figure 12. Path planning diagram for dynamic adjustment phase

图12. 动态调整阶段路径规划图

根据运行结果可知新增订单后，得出的最优路径结果总成本为877.97元，其他具体数据见表6：

Table 6. Optimal path result after adding new order at 11:30

表6. 11:30新增订单后最优路径结果

以下是进行不同算法的成本水平对比分析，见图13，前文在预优化模型的基础上进行动态调度，所以本部分只针对预优化模型所采用的混合遗传蚁群算法进行单遗传算法结果对比，此处为了证明模型的可行性以及算法的有效性，在不改变订单数量、模型参数设置和算法参数设置的前提下，以实验结果为依据，证明模型有效性以及算法的更优性。

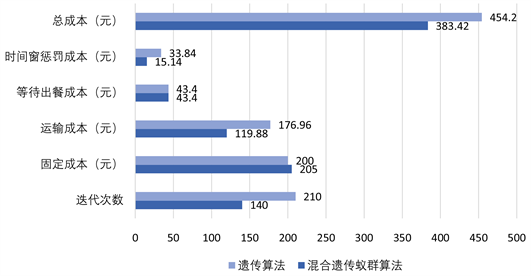
Figure 13. Comparison of cost levels of different algorithms

图13. 不同算法成本水平对比

根据上图13可以看出，遗传算法相较于本文所使用的混合遗传蚁群算法，其运行达到收敛的迭代次数要更长，在派出车辆数目上，二者差距不大，分别是41辆和40辆，但是运输成本上存在57.08元的差距，说明通过遗传算法得到的配送路径长度较长，在配置条件相同的基础上，本文所采用的算法可以减少更多的配送距离，同时也更大程度上降低超时率，节约配送时间，实现更优的路径规划。

5. 结论

本文针对外卖专送模式下多配送中心外卖配送路径优化问题设计了改进的混合遗传蚁群算法以及遗传算法进行求解，设计适合多配送中心路径优化的编码和修正策略，设计进化算子，验证了生成路径结果的合理性，并通过不同算法的对比，证明了本文所采用算法能够有效缩短配送车辆的运输距离，从而减少运输成本，预优化阶段客户满意度达到90%以上，随着订单量的动态变化，通过分时段动态调整来合理规划路径，得出了最优的路径规划结果。