1. 引言
各类物理教材 [1] [2] [3] [4] 或相关辞书 [5] [6] 书的编写,通常都有动能定理的概念,但总都没有势能定理这一概念。然而,有学者认为,在物理教学和物理教材编写及物理科学研究中引入或建立势能定理概念很有必要性和重要性。甚至有些高等院校教师在通过自媒体平台发布的教学视频或教学文稿等文献 [7] [8] [9] 中通过特定的单一保守力场案例引入了势能定理概念,并对其内涵予以表述。
长期以来,有不少物理教育教学工作者及一线物理教师对物理教学和物理教材编写及物理科学研究中是否适宜引入或建立势能定理概念这一问题感到纠结。
为此,本文综合物理概念的形成、内涵和外延以及动能定理的表述、势能的引入和保守力做功对势能变化的影响等角度对是否适宜引入或建立“势能定理”予以说明,仅供参考。
2. 物理概念的科学性
一个物理概念的建立,一定要能高度概括某类物理现象的本质属性,要能用之科学的处理某类物理事件或物理问题。也就是说,物理概念具有高度的严肃性和严谨的科学性。
2.1. 物理概念的内涵
某一物理概念的内涵,就是该概念所包括的一切对象的共同的本质属性的总和。事实上,对某一物理概念所下的定义,就是解释该物理概念的内涵,同时指出该物理概念所反映的对象所共有的本质属性的逻辑关系。掌握物理概念的内涵,就是理解物理概念的本质属性。
比如,单位质量的某种物质温度升高或降低1 K所吸收或放出的热量叫作这种物质的比热容。比热容决定于物质本身的性质,与物体的形状、质量、温度变化、吸收或放出的热量无关。比热容的大小可用公式
(1)
来度量。
描述物质升高或降低温度所吸收或放出热量能力的物理量,这就是比热容的内涵。
2.2. 物理概念的外延
某一物理概念的外延,就是适合该物理概念的一切对象范围。不同的物理概念之间,其外延可以存在从属关系。也就是,一个外延很广泛的物理概念,可能包含若干个外延比较窄小的物理概念。
比如,在“机械运动”这一概念的外延中,就包括匀速直线运动、变速直线运动、曲线运动、抛体运动、圆周运动、机械振动、简谐振动、阻尼振动、受迫振动、自由振动等所有类型的机械运动。其中,简谐振动、阻尼振动、受迫振动、自由振动是“机械振动”这一小概念对象的外延等等。
2.3. 物理概念的特点
首先,物理概念具有严谨的科学性和高度的概括性。物理概念是观察、实验和科学思维相结合的产物,是在观察与实验的基础上,经过思维加工,逐步揭示出现象的物理本质属性而形成的,因此,能对同一类物理现象或物理事件的本质属性予以严谨科学的高度概括。
其次,物理概念通常具有定量性。许多物理概念可用定量的方法来描述客观事物的本质属性,比如速度、加速度、电场强度、电阻、热量等,这类物理概念称为物理量。有些物理概念可用定量的方法来描述其它几个物理概念之间的相互关系,比如动能定理、欧姆定律、楞次定律、电磁感应定律、反射定律、折射定律等,这类物理概念称为物理规律。由于物理量具有确定的量的性质,因此总是可以跟数学和测量联系起来。
3. 动能定理的表述
如图1所示,一质量为m的物体在n个性质可以不相同的外力的作用下由位置A运动到位置B。在此过程中,各个力所做的功分别为
、
、
、
、
、
,物体的速度由
变化到
。实践表明,物体的动能增量
(末动能与初动能之差值)可以表示为
(2)
即,物体动能的增量等于合外力对物体所做的功,等于各个外力对物体做功的代数和。这一定量关系就是动能定理。
在动能定理的表述中,各种不同性质的外力所做的功对于物体动能变化的影响,其性质是相同的,也就是具有相同的内涵本质属性,可以相互叠加。因此,动能定理具有物理概念的严谨科学性和高度概括性。
4. 保守力及其做功的特点
4.1. 保守力和非保守力
物体在某种力的作用下,由一个位置运动到另一位置的过程中,若力对物体所做的功与物体的运动路径无关,只与物体的起点位置和终点位置及该力的性质有关,那么这样的力就称为保守力。比如,重力、万有引力、电场力、分子力等都是保守力。
若某种力对物体做功与物体的运动路径有关,那么这种力就称为非保守力。比如,摩擦力就是最为常见的非保守力。
对于弹力是否为保守力或非保守力,应根据实际情况来界定。一定条件下,某弹力所做的功如果不会引起系统机械能的变化,那么该弹力就是保守力,称之为保守弹力;反之,某弹力所做的功如果会引起系统机械能的变化,那么该弹力就是非保守力,称为非保守弹力。
4.2. 几种常见保守力做功的情况
1) 重力做功
在如图2所示的直角坐标系中,设一质量为m物体在重力场中由位置A经某一任意路径运动到位置B。在这一过程中,可求出重力所做的功为
(3)
显然,重力做功只与物体的始末位置有关(严格来说只与物体的始末位置决定的高度差有关),与运动路径无关。
2) 万有引力做功
设相互发生万有引力作用的两质点的质量分别为m1和m2,在如图3所示的极坐标系中,质点m2相
对于质点m1由位置A运动到位置B,m1对m2的万有引力可表示为
(G为万有引力常量)。
在这一过程中,万有引力的做功为
(4)
同样可以看出,万有引力做功只与物体的始末位置有关,与运动路径无关。
3) 保守弹力做功
如图4所示的一维弹簧振子在振动过程中,小球运动到位移为
的位置时,所受弹簧的弹力为
(k为弹簧的劲度系数)。所以,小球由位置A运动到位置B过程中,弹簧对小球所做的功为
(5)
因此,保守弹力做功只与物体的始末位置有关,与运动路径无关。
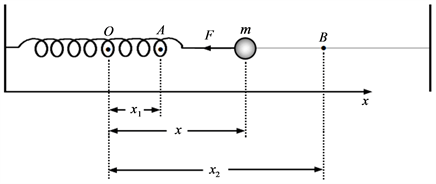
Figure 4. Conservative elastic force doing work
图4. 保守弹力做功
5. 势能及其变化
5.1. 势能的引入
在保守力作用下,物体由一个位置运动到另一个位置的能量变化是确定的。因此,可设想物体处在某一位置时就具有与该位置相对应的一定的能量,这种与物体所在位置有关的能量就称为势能。
物体在某保守力场中某位置Q的势能,等于物体由该位置运动到参考点或参考面(选定势能为0的点或面) O的过程中该保守力
对物体所做的功。势能可表示为
(6)
这一表达式可称为势能的定义式。
如果分别将(3)式、(4)式、(5)式结合(6)式,那么则可分别得出几种不同形式的势能 [10] 表示式。其中,重力势能(选取地面为0势能点)为
(7)
万有引力势能(选取无限远处为0势能点)为
(8)
保守弹力弹性势能(选取弹簧原长位置为0势能点)为
(9)
由(7) (8) (9)式可以看出,物体的势能是位置的单值函数,又称势能函数。还可以根据其它形式的保守力场作用力具体形式求出相应的势能表达式,比如点电荷相互作用的电势能(选取无限远处为0势能点)为
(10)
总之,保守力的形式多样性决定了势能的形式多样性。同时必须明确,势能的定义和保守力做功的特点,决定了势能的内涵本质属性和外延范围,也就是势能仅属于发生相互作用的一对保守力联系的两个物体,即势能的本质属性具有专一性。
5.2. 势能的变化
根据势能的定义式可知,若保守力对物体做功,则物体的势能减少。因此,物体在某保守力作用下由位置A运动到位置B的过程中
(11)
由于在这一过程中,物体势能的增量为
(12)
所以,物体势能的增量等于保守力所做功的负值。
根据势能的专一性不难理解,势能变化也仅属于发生相互作用的一对保守力联系的两个物体,势能变化的本质属性也同样具有专一性。
6. 准势能定理的引入欠科学性
为了表述问题严谨性,这里将前述的自媒体平台发布的相关文献 [7] [8] [9] 中引入的“势能定理”称之为“准势能定理”(因其推理和内涵本质属性的应用欠科学性),将其典型的推理及表述在不改变原文核心内涵的前提下进行简要摘录,并对其欠科学性予以说明。
6.1. 准势能定理的表述摘录
如图5所示,两个质量分别为m1和m2的两个物体1和2组成一个孤立系统,它们之间彼此存在相互作用的保守力。在经过某一过程的相互作用后,它们的速度分别由
变化到
和有
变化到
。根据动能定理,在这一过程中,物体2对物体1所做的功为
(13)
物体1对物体2所做的功为
(14)
所以,保守力对系统所做的总功为
(15)
根据能量守恒定律,仅在保守力相互作用的条件下,系统的动能和势能之和保持不变。因此,系统势能的增量等于动能增量的负值,即
(16)
综合(15)式和(16)式,可得
(17)
由此引入准势能定理这一概念并表述为:物体间相互作用的保守力所做的总功,等于由这些物体组成的系统势能增量的负值。
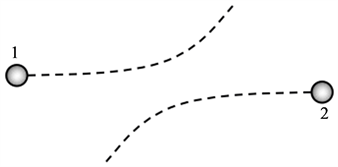
Figure 5. Inference of the quasi potential energy theorem
图5. 准势能定理的推理
6.2. 准势能定理欠科学性
关于准势能定理的(13)式至(17)式的推理仅限于存在一个保守力场而不具普遍性,同时也没有必要性。因为,(13)式至(17)式的推理也仅限于只有保守力做功,而事实上保守力做功与势能变化的关系从前述的(11)式和(12)式即可说明,且跟是否同时有非保守力做功无关。另外,(17)式只对于仅存在一类保守力场的孤立系统才能成立。如果研究系统中同时存在两类(含)以上保守力场时,(17)式就没有实在意义。为了便于描述,仅以两个最简单的模型为例从正反两方面予以说明。
[模型1] 三个物体组成的引力场系统
对于由三个物体1、2、3组成的引力场系统,(17)式可改写为
(18)
其中,
、
、
分别表示物体1与物体2、物体1与物体3、物体2与物体3之间的万有引力做
功引起的势能变化。
这时,(18)式的右边的
、
、
这三项势能变化均属于机械能范畴,也就是在机械能这一概念的外延范围之内,
、
和
具有相同的内涵本质属性,它们的相互叠加具有实在意义。因
此,这时(18)式具有实在意义,从而说明准势能定理的表述或(17)式在只存在一种保守力场的条件下具有实在意义。
[模型2] 两个物体组成的引力场和库仑力场复合系统
对于由两个带电物体1和2组成的引力场和库仑力场复合系统,(17)式可改写为
(19)
其中,
和
分别是两物体之间由于万有引力做功引起的引力势能变化和由于库仑力做功引
起的电势能变化。
根据各种势能和各种势能变化本质属性的可知,(19)式右边的
和
这两项不同内涵本
质属性的势能变化叠加没有实在意义。然而,在研究势能或势能变化时,通常只考虑相同本质属性的保守力作用相关的势能或引起的势能变化。因此,(19)式没有实在意义,从而说明同时存在两类(含)以上保守力场的情况下,准势能定理的表述或(17)式没有实在意义。
综上所述,准势能定理的外延与内涵本质属性在实际问题研究中不相匹配。因此,准势能定理的表述或(17)式缺乏严谨的科学性。
7. 结论
某一物理概念的引入或建立,必须要能对一定的物理现象、物理事件等具有高度的概括性和严肃、严谨的科学性。否则,仅凭片面的主观认识引入或建立起来的物理概念就不能反映客观物理事实,也就没有用于处理物理实际问题的实在意义。
由于保守力场的多样性和各种势能及势能变化本质属性的所限,同时考虑物理概念引入或建立的科学性要求,在物理教学和物理教材的编写及物理科学研究中不适宜引入或建立势能定理概念。
NOTES
*第一作者。
#通讯作者。