1. 引言
在核工程领域中,几何重复结构是普遍存在的,例如大亚湾核电站的堆芯几何结构就存在两个层级的六面体重复结构周期排列模式。在全堆芯几何中,几何体数量可达数十万,所以面对全堆芯计算的需求,势必要发展针对于几何重复结构的输入方式 [1] 。蒙特卡罗方法被广泛应用于反应堆数值模拟计算中,具有几何描述能力强、计算精度高等优势 [2] [3] 。在国内外开发的蒙特卡罗计算程序中,比如蒙特卡罗粒子输运程序MCNP [4] [5] 、开源蒙特卡罗输运程序OpenMC [6] [7] 、反应堆用蒙特卡罗中子模拟程序RMC [8] [9] [10] 、蒙特卡罗程序Serpent等 [11] [12] ,都具备重复结构建模功能,可以方便地描述核反应堆组件和堆芯的几何重复结构。但是,在堆芯物理热工耦合计算、堆芯燃耗计算时,需要将重复几何结构展开,便于对每个栅元进行计数与相关参数更新等,但是目前主流蒙卡程序均不具备重复结构自动展开功能 [13] [14] [15] [16] 。本文主要研究蒙卡程序对重复结构的识别,实现通用的重复几何建模功能。但是由于重复结构不便建立层级的反应率计数,也无法指定元件层级的材料温度,因此对于这些特定情况,本文研究蒙卡程序重复结构的展开方法并实现相关程序功能,最后选取典型堆芯和组件算例,将重复结构展开前后模型的反应堆有效增殖因子keff和几何模型进行对比,验证本文提出的蒙卡程序重复结构展开方法的正确性。
2. 重复结构的识别
2.1. 重复结构建模方式
重复结构是核工程领域常见的几何模式,在多种类型的反应堆中大量存在。反应堆中用多根相同燃料棒按一定周期模式构成组件,多个相同组件按一定模式布置在反应堆堆芯中。为了能够使用较为简便的方式描述全堆芯几何,国内外开发的一些蒙特卡罗程序具有重复结构建模功能。重复结构的实现是通过多层级结构建模的方式。在层级结构建模中,通过填充关系将几何模型划分为不同层级,每个层级表示一个几何空间,每个层级通过某种填充方式在空间中形成有限或者无限的周期重复,再在其上层增加一个边界限制以实现重复结构对有限空间的填充,这实际上就实现了重复结构功能 [17] [18] 。在以上的设计中,重复结构模式可以是有限或无限,单一重复或者复合重复都可以支持。因此,重复结构是可以把同样的几何层级填充在多个位置上,也可以不同的几何层级按照特定顺序填充在同一位置 [19] 。但是从一般计算效率和实际需求来说,常见的重复结构填充方式可以是平行六面体重复、六棱柱重复或者有限圆周重复 [20] ,如图1、图2、图3所示。在填充过程中可以对用于填充的层级进行某种坐标变换、平移或是旋转。

Figure 1. Schematic diagram of the repeated structure of parallelepiped
图1. 平行六面体重复结构示意图
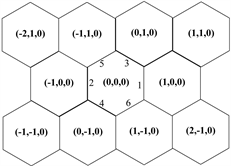
Figure 2. Schematic diagram of the repeated structure of hexagonal prism
图2. 六棱柱重复结构示意图
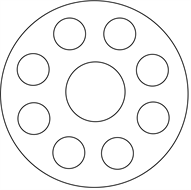
Figure 3. Schematic diagram of the repeated structure of finite circle
图3. 有限圆周重复结构示意图
2.2. 重复结构识别方法
重复结构识别方法实际上是对重复结构相关信息的识别,并将其与输运计算模块衔接的过程。但对反应堆堆芯进行模拟计算时,从燃料棒到组件再到堆芯,从内向外进行建模。几何模型信息主要包括三部分:栅元部分、几何部分、材料部分 [21] [22] 。所以在这个过程中,不仅是对重复结构相关信息的识别,还包括对于用户输入的几何模型的整体信息的识别。
重复结构识别方法主要包括两部分,第一部分是对栅元上的层级进行处理,第二部分是对每个层级进行处理。这样分别从栅元方面和层级方面对重复结构进行处理,能够更好地了解重复几何结构模型的整体情况。
从栅元方面对重复结构进行处理的具体流程图,如图4所示,主要是在已有几何信息的基础上,从栅元方面对重复结构的信息进行整合,主要包括:确定栅元所在层级,并确定是该层级的第几部分;确定栅元是Lattice阵列填充还是单独的Fill填充;如果是Lattice阵列填充的栅元,遍历所有Cell,确定填充该重复结构的每个重复栅元所在的栅元。

Figure 4. Flowchart of hierarchical processing on cell
图4. 栅元上的层级处理流程图
从层级方面对重复结构进行处理的具体流程图,如图5所示,主要是从层级方面对重复结构的信息进行整合,主要包括:确定每一层级填充的重复栅元所在的栅元,使得用户可以更精确地指定某个层级位置上特定的Cell;确定每个层级有多少栅元填充,并确定每个层级填充的最底层无重复几何栅元的数量,能够更好地验证重复结构展开为最底层无重复几何栅元的正确性。
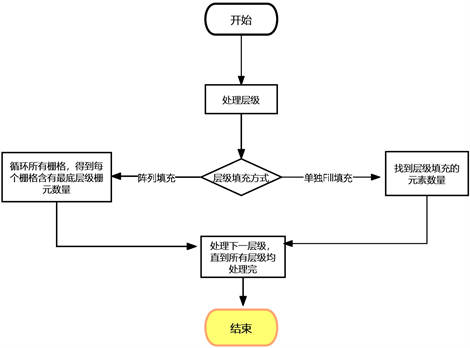
Figure 5. Hierarchical processing flowchart
图5. 层级处理流程图
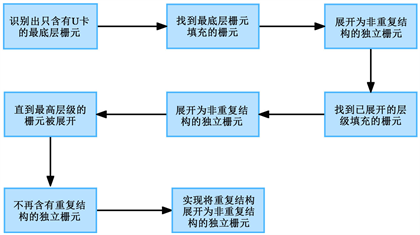
Figure 6. Flowchart of the unfolding of repeated structures
图6. 重复结构展开流程图
3. 重复结构展开方法
由于在堆芯物理热工耦合计算、燃耗计算时,重复结构不便建立层级的反应率计数,也无法指定元件层级的材料温度,对于这些特定情况,需要研究蒙卡程序重复结构的展开方法。
重复结构展开方法是实现将模块阵列形式描述的重复几何栅元展开为最底层级的无重复几何独立栅元。这种方法主要采用“自下而上”的方式,如图6所示。首先根据重复结构识别方法了解的有关重复结构的信息,识别出最底层级包含的栅元,即没有被其他层级填充的栅元。遍历所有栅元,找到只由最低层级填充的栅元,将该栅元信息和最低层级信息进行整合后,将该栅元展开为无重复结构的独立栅元,这就是完成第一层级的展开。找到已展开层级填充的栅元,将其和已展开层级的信息进行整合,实现该栅元的展开。按照这个方法,一层层往上展开,直到最高层级所在栅元均被展开为止。由于重复结构是可以把同样的几何层级填充在多个位置上,也可以不同的几何层级按照特定顺序填充在同一位置,这会使展开过程会变得更加复杂,所以重复结构的识别方法是至关重要的。
3.1. 重复栅元的定位
重复栅元的定位是指确定重复结构中每个重复栅元的位置,就可以计算得到重复栅元在该重复结构中的相对坐标,从而确定该重复栅元的相对于中心重复栅元的平移距离。重复结构中,常见的重复模式有平行六面体重复、六棱柱重复、圆周等分有限重复。其中,前两种重复模式属于线性重复。
线性重复模式是指同一种栅元在空间中线性拓展,各个栅元之间通过平移可以重合。在图7中可以看到:如果以左下角这个栅元的中心为原点,那么栅元(1, 0)可以是栅元(0, 0)按向量b2平移后的结果,同理有栅元(0, 1)。对于这样的线性重复模式,我们称{b1, b2}是该线性模式的重复基,显然各个重复基底之间应该是线性无关的。有了重复基,就可以由重复栅元的位置(k1, k2)得到相对坐标(x, y),从而得到平移的距离。
3.1.1. 平行六面体重复结构的相对坐标确定
对于六面体重复结构,确定重复结构中重复栅元(0, 0)的位置,确定六面体重复结构栅元的排列规律,如图1所示,从而确定每个重复栅元的位置(k1, k2)。对于六面体重复结构这种线性重复模式,其重复基向量b1和b2为栅格增加的方向如图7所示,其表达式为:
(1)
(2)
式中,L1和L2分别为相邻栅元之间的栅距,θ为向量b1和b2之间的夹角。设定重复栅元(0, 0)的中心A点的坐标为(0, 0),待确定的重复栅元中心M点的坐标为(x, y),根据其与重复基向量的表达式:
(3)
从而得到M点的坐标的表达式:
(4)
(5)

Figure 7. Schematic diagram of the repeated structures of parallelepiped
图7. 平行六面体重复结构示意图

Figure 8. Schematic diagram of repeated structures of hexagonal prism
图8. 六棱柱重复结构示意图
3.1.2. 平行六面体重复结构的相对坐标确定
对于六棱柱重复结构,确定重复结构中重复栅元(0, 0)的位置,确定六棱柱重复结构栅元的排列规律,如图2所示,从而确定每个重复栅元的位置(k1, k2)。对于六面体重复结构这种线性重复模式,其重复基向量b1和b2为栅格增加的方向如图8所示,其表达式为:
(6)
(7)
式中,L1和L2分别为b1和b2方向的栅距。设定重复栅元(0, 0)的中心A点的坐标为(0, 0),待确定的重复栅元中心M点的坐标为(x, y),根据其与重复基向量的表达式:
(8)
从而得到重复栅元中心位置坐标M点的表达式:
(9)
(10)
3.2. 重复结构范围的确定
重复结构填充范围的确定是指用一种重复结构填充了某上层栅元后,如果对重复结构进行展开,需要知道上层栅元的边界范围,判断上层边界范围是否对下层的重复结构进行切割。但下层的重复结构并不知道被哪个上层栅元所引用,也不知道引用了多大的空间,这些都需要由上层栅元的边界来确定,这就用到重复结构识别功能,确定上层的栅元和下层的重复结构的关联。根据已知的重复结构中每个栅元的位置和上层栅元的边界范围,重复结构被上层栅元切割,重复栅元主要分为三种情况:① 该重复栅元在上层边界范围内,没有被切割,该重复栅元几何范围没有发生变化;② 该重复栅元被上层边界切割了部分几何,需要合并上下层级的边界关系,生成新的边界表达式,并尽可能地进行化简,如图9所示;③ 该重复栅元完全被上层边界切掉,在重复结构展开,这类是需要被剔除的冗余栅元,不需要生成新的栅元。

Figure 9. Schematic diagram of hierarchical boundary synthesis
图9. 层级边界合成示意图
3.3. 重复栅元号的定义
将重复结构展开为无重复几何的独立栅元,在确定重复栅元在上层栅元范围内,需要对展开后的独立栅元生成栅元号。展开前,重复结构不便于直接指定每个重复栅元的栅元号。在展开过程中,对新生成的栅元按照一定的规律进行编号,使用户可以精确地指出重复结构中某个特定位置的栅元,便于指定该栅元材料温度以及对该栅元进行反应率计数。
3.4. 重复栅元曲面的生成
将重复结构展开为无重复几何的独立栅元,在确定重复栅元在上层栅元范围内,就需要对展开的栅元生成新的曲面。确定栅格元素中心坐标的位置后,由用户输入的曲面方程和中心坐标平移的距离,对每个重复栅元生成新的曲面方程,其中需要对新生成曲面系数取一个合适的精度,不同栅格之间必须能够精确连接起来,使模型达到合理的结构,不能出现未定义的区域,也不能有重叠区域,否则在运行文件时会出现粒子丢失的错误从而导致运行失败。由于相邻的重复栅元会生成相同的曲面方程,就会产生重复面。首先,通过手动删除重复面的方式,验证了重复面对计算结果没有影响。现在在合并新生成曲面中重复面的工作,已经将曲面卡中的重复面删除,正在进行栅元卡中已删除曲面的曲面号的替换工作。
4. 算例验证与结果分析
本文算例计算使用的截面数据为ENDF/B-VII数据库的连续能量截面数据。计算条件是每代15,000个粒子,计算200代,统计后150代,初始源取为几何中心位置的点源。
为了测试重复结构展开后结果的正确性,将对keff进行比较来验证结果的正确性,结合统计误差(σ)用来确定结果是否在统计上具有一致性,当差异在±3σ间内(置信度为99.6%)时,可以认为结果在统计上是相同的。σ定义为:
(11)
式中,σ1和σ2分别为重复结构展开前和展开后的keff标准偏差。
4.1. 小型堆算例
该小型堆算例含有三层重复结构,且重复结构是六面体填充。小型堆堆芯由9个燃料组件排列成正方形栅格,每个燃料组件的截面为21.4215 × 21.4215 cm2的正方形栅格,其燃料组件根据填充不同分为三种不同类型,整个堆芯被一层反射层组件包围。每个燃料组件包含17 × 17个燃料棒,每个燃料棒的截面为1.26015 × 1.26015 cm2的正方形栅格。

Table 1. keff value before and after the unfolding of the repeated structures in example 1
表1. 算例1重复结构展开前后的keff
 (a)
(a)  (b)
(b)
Figure 10. Schematic diagrams of core before and after the unfolding of the repeated structures in example 1: (a) Before unfolding; (b) After unfolding
图10. 算例1重复结构展开前后堆芯示意图:(a) 展开前;(b) 展开后
该算例展开了三层重复结构,展开了4624个燃料棒,展开后7858个栅元、20,933个曲面。表1展示了算例1中重复结构展开前和展开后的计算结果,包括有效增值因数keff、标准偏差、展开前后keff的偏差和3σ。从表中计算结果中可以看出,展开前和展开后的keff之间的偏差为36 pcm,在±3σ以内,说明对于keff的计算,展开前后的结果吻合得比较好。
图10分别是重复结构展开前和展开后堆芯示意图,可以看出展开后几何模型并未变化,说明重复结构展开前后在几何模型方面吻合得比较好。
4.2. 大亚湾组件算例
该算例含有两层重复结构,且重复结构是六面体填充。该算例是大亚湾其中的一个燃料组件,该组件由17 × 17个燃料棒排列成正方形栅格,每个燃料棒的截面为1.26 × 1.26 cm2的正方形栅格。
该算例展开了两层重复结构,展开了289个燃料棒,展开后1275个栅元、1884个曲面。表2展示了算例2中重复结构展开前和展开后的计算结果,包括有效增值因数keff、标准偏差、展开前后keff的偏差和3σ。从表中计算结果中可以看出,展开前和展开后的keff之间的偏差为187 pcm,在±3σ以内,说明对于keff的计算,展开前后的结果吻合得比较好。
图11分别是重复结构展开前和展开后组件示意图,可以看出展开后几何模型并未变化,说明重复结构展开前后在几何模型方面吻合得比较好。

Table 2. keff value before and after the unfolding of the repeated structures in example 2
表2. 算例2重复结构展开前后的keff
 (a)
(a)  (b)
(b)
Figure 11. Schematic diagrams of core before and after the unfolding of the repeated structures in example 2: (a) Before unfolding; (b) After unfolding
图11. 算例2重复结构展开前后堆芯示意图:(a) 展开前;(b) 展开后
4.3. 研究堆算例
该算例含有五层重复结构,且重复结构是六棱柱填充。该研究堆堆芯是由7 × 7组件排列成六棱柱栅格,每个燃料组件由15 × 15个燃料棒构成,堆芯还包括控制棒组件。
该算例展开了五层重复结构,展开了19个燃料组件和12个控制棒组件,展开了5491个燃料棒,展开后26,482个栅元、95,293个曲面。表3展示了算例3中重复结构展开前和展开后的计算结果,包括有效增值因数keff、标准偏差、展开前后keff的偏差和3σ。从表中计算结果中可以看出,展开前和展开后的keff之间的偏差为95 pcm,在±3σ以内,对于keff的计算,展开前后的结果吻合得比较好。验证了重复结构展开模块的可靠性。
图12分别是重复结构展开前和展开后堆芯示意图,可以看出展开后几何模型并未变化,说明重复结构展开前后在几何模型方面吻合得比较好。

Table 3. keff value before and after the unfolding of the repeated structures in example 3
表3. 算例3重复结构展开前后的keff
 (a)
(a) 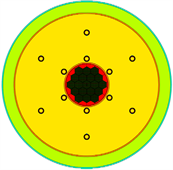 (b)
(b)
Figure 12. Schematic diagrams of core before and after the unfolding of the repeated structures in example 3: (a) Before unfolding; (b) After unfolding
图12. 算例3重复结构展开前后堆芯示意图:(a) 展开前;(b) 展开后
为了验证蒙卡程序重复结构展开方法的正确性,首先利用上述三个算例对比了重复结构展开前后的keff的误差,然后利用上述三个算例对比了重复结构展开前后几何模型的变化,对比结果符合良好,验证了蒙卡程序重复结构展开方法的正确性。
5. 结论
由于蒙卡程序在物理热工耦合、燃耗计算时需要对重复结构的识别和展开进行处理,本文首先研究了蒙卡程序对重复结构的识别方法;其次,研究了蒙卡程序重复结构的展开方法,将重复几何栅元展开为最底层无重复几何的独立栅元。最后,选取小型堆、大亚湾组件以及研究堆为算例验证结果的正确性,小型堆展开了三层重复结构,展开了4624个燃料棒,展开后7858个栅元、20,933个曲面;大亚湾组件算例展开了两层重复结构,展开了289个燃料棒,展开后1275个栅元、1884个曲面;研究堆算例展开了五层重复结构,展开了19个燃料组件和12个控制棒组件,展开了5491个燃料棒,展开后26,482个栅元、95,293个曲面。并将重复结构展开前后的keff和几何模型进行对比,验证了蒙卡程序重复结构展开方法和功能的正确性。
基金项目
国家磁约束核聚变能发展研究专项(2019YFE03110000, 2019YFE03110003)。
NOTES
*通讯作者。