一类可压缩超弹性材料的圆柱空穴现象的定性分析

Qualitative Analysis of Cylindrical Cavitation in a Class of Compressible Hyperelastic Materials

摘要: 本文主要研究了一类可压缩超弹性材料的实心圆柱体的径向有限变形问题，通过理论解和数值模拟，我们得到了一些有趣的结论。存在一个临界拉伸值，当径向拉伸小于临界值时，圆柱体保持为实心圆柱体，当径向拉伸大于临界值时，圆柱体轴线上会形成圆柱空穴。应力集中和突变现象进一步表明，可压缩超弹性圆柱体中的空穴现象符合实际的物理背景。

Abstract: In this paper, the finite radial deformation of a solid cylinder made of a class of compressible hyperelastic materials is studied. Through theoretical solutions and numerical simulations, we obtain some interesting conclusions. However, there is a critical stretching value. When the radial stretching is less than the critical value, the cylinder remains a solid cylinder. When the radial stretching is greater than the critical value, a cylindrical cavity will form on the axis of the cylinder. Furthermore, the stress concentration and abrupt change phenomenon shows that the cavity phenomenon in the compressible hyperelastic cylinder is in line with the actual physical background.

1. 引言

在实际应用中，人们普遍认识到在物体内部空穴(空化)的突然形成和生长是材料被破坏的先兆。Gent和Lindly 1958年便在文献 [1] 中对硫化橡胶材料内部的空穴生成的实验结果进行了研究分析。基于非线性弹性理论，作者在文献 [2] 中将超弹性材料中的空穴现象描述为一类数学模型中的分岔问题，从而为研究此类问题奠定了理论基础。文献 [3] 不仅证明了超弹性材料中的空穴现象可以用材料中的预存微孔的增长现象解释，而且指出了这类现象是一类固有的非线性问题，不能用线性方法来研究。另一方面，空穴现象的出现，主要是由于材料的不稳定性引起的，它可以看成材料损伤和破坏的一个重要机理，因此如何预测材料内部空穴的生成和增长引起了广大学者的兴趣。Horgan和Polignone在文章 [4] 中对1995年之前关于不可压缩和可压缩超弹性材料中的空穴现象的相关研究结果进行了全面的回顾，袁等人对2005年之前的结果进行了全面的回顾，见 [5] 。对于由一类均匀各向同性可压缩的广义Varga材料组成的实心圆柱体，袁等人 [6] 研究其在给定的外表面拉伸和轴向拉伸或压缩共同作用下的轴对称变形问题。利用能量变分原理得到了问题的控制方程和边界条件，并求得了描述柱体径向对称变形的参数型解析解和描述圆柱体轴线上空穴生成和增长的空穴分岔解。给出了与泊松比和轴向伸长相关的径向临界伸长的表达式和空穴生成后的应力表达式；并通过数值算例讨论了这些参数对圆柱体轴线上空穴生成和增长、圆柱体的径向位移以及应力的集中和突变的影响，同时给出了相应的数值模拟。特别地，对于可压缩超弹性材料中的球形空化，相关的研究成果可见文献 [7] [8] [9] 。然而，对于可压缩超弹性材料，由于问题固有的非线性性，要得到描述球体或柱体中空穴的生成和增长问题的解析解非常困难，它严格依赖于组成球体或柱体的材料的本构关系。文献 [2] 对问题的解的存在性、唯一性以及稳定性进行了分析，最近，文献 [8] [10] 分别研究了几类特殊材料球体中的空穴分岔问题，并且求得了问题的解析解。

本文我们主要考虑的是一类可压缩超弹性材料组成的固体圆柱体在给定的表面拉伸作用下的空穴生成和增长问题。在第二节中，我们利用非线性弹性有限变形理论建立了相应的数学模型，给出了描述柱体径向对称变形的控制方程和边界条件。在第三节中，求得了径向对称变形的参数型解析解，证明了对任意给定的表面伸长，满足边界条件的控制方程恒存在一个对应于柱体内部的均匀变形的平凡解；当外表面伸长超过临界值时，控制方程有两个解，一个是平凡解，另一个是非平凡解，称之为空穴分岔解，它对应于柱体内部的空穴的生成和增长。为了更好地理解本文的结论，在第四节中我们给出了一些数值模拟，说明了柱体表面发生空穴分岔时的景象、环向应力分析。

2. 模型的数学描述

2.1. 控制方程和边界条件

假设由均匀各向同性的可压缩超弹性材料组成的实心圆柱体的半径为A，我们主要考察的是柱体在表面均布的径向拉伸作用下的有限变形问题。在柱坐标系中，假设 $\left(R,\Theta ,Z\right)$ 和 $\left(r,\theta ,z\right)$ 分别表示柱体中变形前和变形后的点，在径向对称变形和平面应变状态的假设下，变形分量和主拉伸 ${\lambda }_i\left(i=1,2,3\right)$ 分别为

$r=r\left(R\right)>0,0<R\le A,r\left(0+\right)\ge 0;\theta =\Theta ;z=Z,$ (1)

${\lambda }_1=r^{\prime }\left(R\right),{\lambda }_2=r\left(R\right)/R,{\lambda }_3=1.$ (2)

其中 $r\left(R\right)\ge 0$ 为待求解的径向变形未知函数， $r^{\prime }\left(R\right)$ 表示关于自变量R的导数。有趣的是，如果 $r\left(0+\right)=0$ ，则说明圆柱体在当前结构中是实心的；当 $r\left(0+\right)>0$ 时，此时假设空穴表面是无约束的，则在圆柱体的中心有一个半径为 $r\left(0+\right)$ 的柱形空穴生成。

同时，为了确保是径向对称的变形，我们假设有 ${\lambda }_1{\lambda }_2{\lambda }_3>0$ ，故由等式(2)可得

$r^{\prime }\left(R\right)>0,0<R\le A\text{.}$ (3)

对应于径向对称变形的Cauchy应力张量的分量由下式给出：

${\tau }_{rr}\left(R\right)=\frac{1}{{\lambda }_2{\lambda }_3}\frac{\partial W}{\partial {\lambda }_1}$ , ${\tau }_{\theta \theta }\left(R\right)=\frac{1}{{\lambda }_1{\lambda }_3}\frac{\partial W}{\partial {\lambda }_2}$ , (4)

其中 $W=W\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$ 是组成圆柱体的可压缩超弹性材料对应的应变能函数。如果我们忽略体积力，则描述圆柱体径向对称变形的微分方程组可简化一个方程，即

${\tau }_{rr}\left(R\right)+\frac{r^{\prime }\left(R\right)}{r\left(R\right)}\left[{\tau }_{rr}\left(R\right)-{\tau }_{\theta \theta }\left(R\right)\right]=0.$ (5)

将(4)代入方程(5)，则平衡微分方程可化为如下的二阶常微分方程：

$\frac{{\partial }^{2}W}{\partial {\lambda }_1^2}{r}^{″}\left(R\right)+\frac{1}{R}\frac{{\partial }^{2}W}{\partial {\lambda }_1\partial {\lambda }_2}\left(r^{\prime }\left(R\right)-\frac{r\left(R\right)}{R}\right)+\frac{1}{R}\left(\frac{\partial W}{\partial {\lambda }_1}-\frac{\partial W}{\partial {\lambda }_2}\right)=0.$ (6)

进一步，假设在柱体表面上给定径向伸长 $\lambda >1$ ，则边界条件需满足

$r\left(A\right)=\lambda A.$ (7)

同时在圆柱的轴线上，另一边界条件满足：

$r\left(0+\right){\tau }_{rr}\left(0+\right)=0.$ (8)

边界条件(8)式表明：若在柱体内部没有空穴生成，则有 $r\left(0+\right)=0$ ；反之，若在柱体轴线上有空穴生成，即 $r\left(0+\right)>0$ ，那么对不受约束的空穴表面， ${\tau }_{rr}\left(0+\right)=0$ 成立。

2.2. 应变能函数

我们知道，各向同性超弹性材料的本构关系可以由下面的应变能函数来给出，参见文献 [11]

$W=W\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$ (9)

这里 $W\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)$ 是 ${\lambda }_1,{\lambda }_2,{\lambda }_3$ 的对称函数， ${\lambda }_1,{\lambda }_2,{\lambda }_3$ 是应变张量的主值。在本文的研究中，我们主要考虑的是一类特殊的超弹性材料模型。假设圆柱体由一类特殊的各向同性可压缩超弹性材料组成，其应变能函数W可表示为：

$W=W\left(i_1,i_2,i_3\right)=k_1\left(i_1-3\right)+g\left(i_2\right)+k_3\left(i_3-1\right)$ , (10)

其中

$i_1={\lambda }_1+{\lambda }_2+1$ , $i_2={\lambda }_1{\lambda }_2+{\lambda }_1+{\lambda }_2$ , $i_3={\lambda }_1{\lambda }_2$ (11)

是变形梯度张量的主不变量，g是一个二次连续可微的非线性函数， $k_1,k_3$ 是两个与材料有关的常数。

在自然情况下，为了确保各向同性的超弹性材料对应的应变能函数(9)的线性化与经典的线性理论一致(见 [9] )，应变能函数W应满足：

$W\left(3,3,1\right)=k_1\left(3-3\right)+g\left(3\right)+k_3\left(1-1\right)=0,$ (12)

$\frac{\partial W}{\partial {\lambda }_1}\left(3,3,1\right)=k_1+g^{\prime }\left(i_2\right)\left({\lambda }_2+1\right)+k_3{\lambda }_2=0.$ (13)

进一步，可以得到

$g\left(3\right)=0$ , $g^{\prime }\left(3\right)=-\left(k_1+k_3\right)/2$ , (14)

其中 $g^{\prime }$ 表示对 $i_2$ 的一阶导数。同时，为了确保材料的力学行为的合理性，应变能函数还须满足Legendre- Hadamard不等式或强凸性条件，即

$g^{″}\left({\lambda }_1{\lambda }_2{\lambda }_3\right)>0.$ (15)

因此由控制方程(6)、应变能函数(10)以及边界条件(7)和(8)组成了可压缩超弹性材料模型。

3. 模型的解和定性分析

3.1. 解析解与空穴分岔解

显而易见，对任意给定的径向伸长 $\lambda >1$ ，满足边界条件(7)和(8)的齐次解为

$r\left(R\right)=\lambda R$ , (16)

其对应于柱体内部的径向位移 $U\left(R\right)=\left(\lambda -1\right)R$ 。将方程(10)代入(6)，进一步得到

$g^{″}\left(i_2\right){\left({\lambda }_2+1\right)}^2{r}^{″}\left(R\right)+\frac{1}{R}\left[g^{″}\left(i_2\right)\left({\lambda }_1+1\right)\left({\lambda }_2+1\right)\left({\lambda }_1-{\lambda }_2\right)\right]=0.$ (17)

进一步，较容易求得

$\frac{\text{d}{i}_2}{\text{d}R}=\left({\lambda }_2+1\right)r^{″}\left(R\right)+\frac{1}{R}\left({\lambda }_1+1\right)\left({\lambda }_1-{\lambda }_2\right)$ , (18)

这里 $i_2$ 由方程(11)中的第二个方程给出。则式(17)可写为

$\left({\lambda }_2+1\right)g^{″}\left(i_2\right)\frac{\text{d}{i}_2}{\text{d}R}=0.$ (19)

由式(2)可知 ${\lambda }_2+1>0$ ，从而由(15)以及(17)可得到 $\frac{\text{d}{i}_2}{\text{d}R}=0$ ，即

$i_2=r^{\prime }\left(R\right)\left(\frac{r\left(R\right)}{R}+1\right)+\frac{r\left(R\right)}{R}=k_1$ , (20)

这里 $k_1$ 为一大于0积分常数。进一步，由(20)可解得径向变形函数的通解解析式为

$r\left(R\right)={\left[\left(k_1+1\right)R^2+k_2\right]}^{1/2}-R$ , (21)

其中 $k_2\ge 0$ 也是一个积分常数。

接下来，我们将利用边界条件(7)和(8)来确定积分常数 $k_1$ 和 $k_2$ 的值。利用外边界条件(7)，我们可得

$k_2=\left[{\left(\lambda +1\right)}^2-\left(k_1+1\right)\right]A^2=\left({\lambda }^2+2\lambda -k_1\right)A^2$ . (22)

由式(21)和(22)，进一步可得到

$r\left(0+\right)=k_2^{1/2}={\left[{\lambda }^2+2\lambda -k_1\right]}^{1/2}A\ge 0$ . (23)

将式(10)代入方程(4)的第一个方程，有

${\tau }_{rr}\left(R\right)=\frac{1}{{\lambda }_2}\left[c_1+g^{\prime }\left(i_2\right)\left({\lambda }_2+1\right)+c_3{\lambda }_2\right]=\frac{R}{r\left(R\right)}{c}_1+\left(\frac{R}{r\left(R\right)}+1\right)g^{\prime }\left(i_2\right)+c_3$ . (24)

由(24)和内边界条件(8)，求得

$r\left(0+\right)\left[g^{\prime }\left(k_1\right)+c_3\right]=0$ . (25)

结合以上分析，对于任意给定的径向伸长 $\lambda >1$ ，由(21)、(22)以及(25)可得 $r\left(0+\right)=0$ 。这说明当 $k_2=0$ ，这时 $k_1={\lambda }^2+2\lambda$ ，因此圆柱体内部的均匀变形解为 $r\left(R\right)=\lambda R$ 。然而，如果存在一常数 $k_1>0$ ，满足 $g^{\prime }\left(k_1\right)+c_3=0$ ，那么可由从方程 $k_2=\left({\lambda }^2+2\lambda -k_1\right)A^2$ 求解出 $k_2$ 的值，由此说明，满足边界条件的控制方程(6)有两个解，除平凡解 $r\left(R\right)=\lambda R$ 外，还有一个解即为式(20)。

在柱体中心，对于任意给定的径向伸长 $\lambda >1$ ，方程(25)的一个解 $r\left(0+\right)=0$ 称之为方程的一个平凡解；同时，通过前面的计算可知，在柱体轴线上有空穴生成时的临界伸长为：

${\lambda }_{cr}={\left(1+k_1\right)}^{\frac{1}{2}}-1$ . (26)

也就是说，方程(25)在临界点 $\left(0,-1+{\left(1+k_1\right)}^{\frac{1}{2}}\right)$ 处从平凡解 $r\left(0+\right)=0$ 处发生分岔现象，非平凡解由 $r\left(0+\right)=k_2^{\frac{1}{2}}={\left({\lambda }^2+2\lambda -k_1\right)}^{\frac{1}{2}}A\ge 0$ 给出(表示空穴生成后的半径)，其中 ${\lambda }_{cr}=-1+{\left(1+k_1\right)}^{\frac{1}{2}}$ ，且由方程 $g^{\prime }\left(k_1\right)+c_3=0$ 可以确定 $k_1$ 的值，从而称方程(25)为空穴分岔方程。此外，由(26)知，柱体内部发生空穴分岔时的临界伸长与材料常数无关。

进一步，如果 $\lambda <{\lambda }_{cr}$ 时，则与均匀变形解相对应的径向位移为

$U\left(R\right)=r\left(R\right)-R=\left(\lambda -1\right)R$ . (27)

反之，当 $\lambda >{\lambda }_{cr}$ 时，这时与空穴生成后的解 $r\left(R\right)={\left[\left(k_1+1\right)R^2+k_2\right]}^{1/2}-R$ 相对应的径向位移变为

$U\left(R\right)={\left[\left(k_1+1\right)R^2+\left({\lambda }^2+2\lambda -k_1\right)A^2\right]}^{\frac{1}{2}}-2R$ . (28)

3.2. 圆柱体的应力分布

在本小节中，我们将考虑圆柱体发生空穴分岔时的应力分布，这里有两种可能的情况：

(1) 当 $\lambda \le {\lambda }_{cr}$ 时，则对应于均匀变形解为 $r\left(R\right)=\alpha R$ ，同时 ${\lambda }_1={\lambda }_2=\alpha$ ， ${\lambda }_3=1$ ，这意味着圆柱体内部的径向应力和环向应力相等，即有

$\begin{array}{c}{\tau }_{rr}\left(R\right)={\tau }_{\theta \theta }\left(R\right)=\frac{1}{{\lambda }_2}\frac{\partial W}{\partial {\lambda }_1}=\frac{1}{{\lambda }_2}\left[c_1+g^{\prime }\left(i_2\right)\left({\lambda }_2+1\right)+c_3{\lambda }_2\right]\\ =\frac{1}{\alpha }{c}_1+g^{\prime }\left({\alpha }^2+2\alpha \right)\left(1+\frac{1}{\alpha }\right)+c_3.\end{array}$ (29)

(2) 当 $\lambda >{\lambda }_{cr}$ 时，即 $g^{\prime }\left(k_1\right)+c_3=0$ ，这时柱体表面的径向应力和环向应力分别为

$\begin{array}{c}{\tau }_{rr}\left(R\right)=\frac{1}{{\lambda }_2}\frac{\partial W}{\partial {\lambda }_1}=\frac{1}{{\lambda }_2}\left[c_1+g^{\prime }\left(k_1\right)\left({\lambda }_2+1\right)+c_3{\lambda }_2\right]\\ =\frac{1}{{\lambda }_2}{c}_1+g^{\prime }\left(k_1\right)\frac{1}{\lambda }+g^{\prime }\left(k_1\right)\frac{1}{{\lambda }_2}+c_3\\ =\frac{1}{{\lambda }_2}{c}_1+g^{\prime }\left(k_1\right)\frac{1}{{\lambda }_2}\\ =\frac{R}{r\left(R\right)}{c}_1+g^{\prime }\left(k_1\right)\frac{R}{r\left(R\right)}\end{array}$ (30)

和

$\begin{array}{c}{\tau }_{\theta \theta }\left(R\right)=\frac{1}{{\lambda }_1}\frac{\partial W}{\partial {\lambda }_2}=\frac{1}{{\lambda }_1}\left[c_1+g^{\prime }\left(k_1\right)\left({\lambda }_1+1\right)+c_3{\lambda }_1\right]\\ =\frac{1}{{\lambda }_1}{c}_1+g^{\prime }\left(k_1\right)\left(1+\frac{1}{{\lambda }_1}\right)+c_3\\ =\frac{1}{r^{\prime }\left(R\right)}{c}_1+g^{\prime }\left(k_1\right)\frac{1}{r^{\prime }\left(R\right)}.\end{array}$ (31)

从而进一步可求得柱体空穴表面的径向应力和环向应力分别为

${\tau }_{rr}\left(0+\right)=0$ , ${\tau }_{\theta \theta }\left(0+\right)=+\infty$ . (32)

4. 数值算例与结果分析

为了进一步证明本文前面所研究的结论，我们不妨假设

$g\left(i_2\right)=c_2\left(\frac{1}{2}{i}_2^2-4i_2+\frac{15}{2}\right)$ ,(33)

较容易证明式(33)满足强凸性条件(15)。利用线性化约束条件(参见 [9] )，我们可得

$c_1=\mu \frac{5-9\nu }{2\left(1-2\nu \right)}$ , $c_2=\mu \frac{1-\nu }{2\left(1-2\nu \right)}$ , $c_3=-\mu \frac{3-7\nu }{2\left(1-2\nu \right)}$ , (34)

其中 $\mu$ 和 $v$ 分别为剪切模量和泊松比。为了确保 $c_1,c_2,c_3$ 均为正，不妨假设有条件

$\mu >0$ , $3/7<\nu <1/2$ . (35)

不失一般性，取

$v=\frac{13}{28}$ ，则 $c_1=\frac{23}{4}$ , $c_2=\frac{15}{4}$ , $c_3=\frac{21}{12}$ ; (36)

$v=\frac{27}{56}$ ，则 $c_1=\frac{37}{4}$ , $c_2=\frac{29}{4}$ , $c_3=\frac{21}{4}$ ; (37)

$v=\frac{25}{56}$ ，则 $c_1=\frac{55}{12}$ , $c_2=\frac{31}{12}$ , $c_3=\frac{7}{12}$ . (38)

由条件 $g^{\prime }\left(k_1\right)+c_3=0$ ，则分别可解得

$k_1=\frac{53}{15}$ , $k_1=\frac{89}{29}$ , $k_1=\frac{117}{31}$ . (39)

进一步，可以求得

$\frac{r\left(0+\right)}{A}={\left[{\left(\lambda +1\right)}^2-\frac{68}{15}\right]}^{1/2}$ (40)

以及

$\frac{U}{A}={\left[\left(k_1+1\right){\left(\frac{R}{A}\right)}^2+\left({\lambda }^2+2\lambda -k_1\right)\right]}^{1/2}-2\frac{R}{A}$ . (41)

注：当 $c_2=0$ 时，则方程(10)对应的材料模型是由Varga提出的，因此当 $c_2\ne 0$ 时，我们称对应于(10)的超弹性材料模型为广义Varga材料。

综上分析可知，该特殊的超弹性材料组成的柱体其内部发生空穴分岔时的径向临界伸长为 ${\lambda }_{cr}=1.1292$ 。通过数值模拟，表示出柱体内部有空穴的生成和增长与给定的表面径向伸长 $\lambda$ 之间的关系，如下图1所示；对于给定表面伸长 $\lambda$ 不同的值，柱体内部的径向位移变化情况，如下图2所示；当表面伸长超过临界值时，柱体内部的应力间断情况见图3表示；对于给定不同的表面伸长，柱体内部的应力分布情况见图4表示。

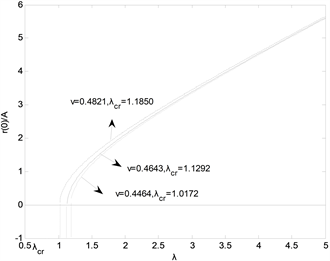
Figure 1. Effect of axial stretch on cavity formation and growth of cylinder

图1. 不同的径向伸长对空穴生成和增长的影响

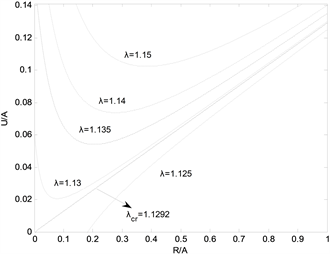
Figure 2. Curves of radial displacement for various values of $\lambda$

图2. 对于不同的 $\lambda$ 值，柱体内部的径向位移曲线

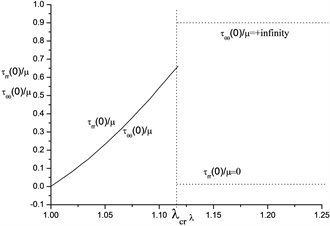
Figure 3. Jumping of stress at the surface of the cavity

图3. 空穴表面的应力跳跃

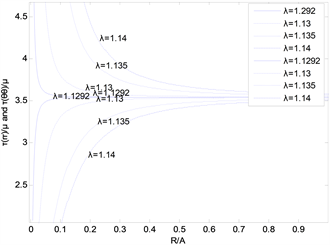
Figure 4. Discontinuity of stresses in the interior of the cylinder

图4. 对于不同的 $\lambda$ 值，柱体内部的应力分布

在本文的研究中，对于给定的表面径向伸长，我们主要分析了可压缩超弹性材料组成的柱体的空穴分岔情况。通过数值模拟，得出了该材料的一些有趣现象，其中应变能量函数由方程(10)给出。我们通过数值模拟说明了当给定的径向伸长超过临界值时，即 $\lambda >{\lambda }_{cr}$ ，在柱体内部有空穴生成并随之增长，如图1所示；由图2可知，当 $\lambda <{\lambda }_{cr}$ 时，整个圆柱体的变形是延伸的，但当 $\lambda >{\lambda }_{cr}$ 时，空穴附近的变形是收缩的；图3表明，当 $\lambda <{\lambda }_{cr}$ 时，径向应力和环向应力的分布均匀，但当 $\lambda ={\lambda }_{cr}$ 时，均匀应力状态有明显的不连续性。如图4所示，当 $\lambda <{\lambda }_{cr}$ 时，径向应力和环向应力的分布是均匀的，当 $\lambda ={\lambda }_{cr}$ 时，应力不连续性出现，而当 $\lambda >{\lambda }_{cr}$ 时，在中心表面附近明显存在环向应力的集中现象，环向应力也会出现同样的情况。