1. 引言
稳健性[1] 考虑的是:当实际模型中的分布与假定模型中的分布有少许差异时,统计方法的性能会受到怎样的影响。因此,在粗差不可避免的情况下,选择适当的估计方法,使所估参数尽可能减免粗差的影响,得出正常模式下最佳或接近最佳的估值。
所谓的尺度参数是指满足分布族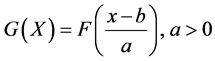 ,这里a便是尺度参数。
,这里a便是尺度参数。
Huber在1981年[2] 就指出,在生产实践和科学实验所采集的数据中,粗差出现的概率为1%~10%,并提到了一些高效稳健的尺度估计,如:四分位距(interquartile range)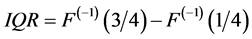 ,中位数绝对偏差(median absolute deviation)
,中位数绝对偏差(median absolute deviation) 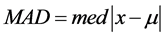 (med表示求中位数,下同)。IQR估计非对称分布的尺度,它的崩溃点(breakdown point)最高可达25%。IQR针对的是对称分布,崩溃点最高可达50%,高斯效为37%,对于非对称分布则不适用。
(med表示求中位数,下同)。IQR估计非对称分布的尺度,它的崩溃点(breakdown point)最高可达25%。IQR针对的是对称分布,崩溃点最高可达50%,高斯效为37%,对于非对称分布则不适用。
Rousseuw-Croux在1933年[3] 依据四分位间距(0.25 quantile of the distances)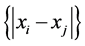 提出了两个更为高效的尺度估计量双中位数两两距离(double median of the pairwise distances)
提出了两个更为高效的尺度估计量双中位数两两距离(double median of the pairwise distances)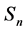 ,其表达式为:
,其表达式为:
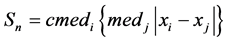
其中c为纠偏因子。
下四分位两两距离(lower quartile of the pairwise distances)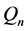 ,表达式为:
,表达式为:
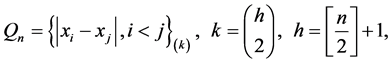
它们的崩溃点均达到50%,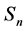 的高斯效可达到58%,
的高斯效可达到58%,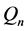 可达到82%。
可达到82%。
Smirnor-Shevlyakov在2014年[4] 针对位置参数为0时,基于 提出了改进的中位数绝对偏差(refinement of the median absolute deviation),即为
提出了改进的中位数绝对偏差(refinement of the median absolute deviation),即为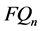 ,其表达式为:
,其表达式为:

其中
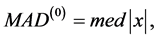
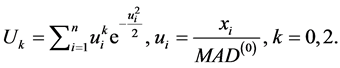
其计算速度为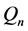 的4~5倍,崩溃点最高可达50%,高斯效可达80%,且更适用于蒙特卡罗模型。
的4~5倍,崩溃点最高可达50%,高斯效可达80%,且更适用于蒙特卡罗模型。
2. 估计量GMAD
基于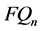 是针对刻度参数在均值为0时构造的估计,自然的想法就是将此估计推广至均值未知的场合。为此,我们构造如下的尺度估计量gmad:
是针对刻度参数在均值为0时构造的估计,自然的想法就是将此估计推广至均值未知的场合。为此,我们构造如下的尺度估计量gmad:

其中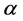 为自由参数,
为自由参数,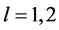 ,l取1时
,l取1时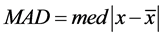 ,
,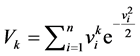 ,
,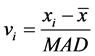 ,
,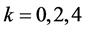 。
。
l取2时,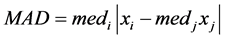 ,
,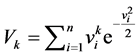 ,
,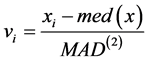 ,
,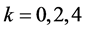 。将
。将 和
和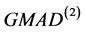 统称为GMAD。
统称为GMAD。
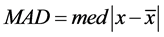 ,用样本均值
,用样本均值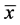 ,估计μ。而
,估计μ。而 ,用样本中位数,估计μ。这两种估计量均是中位数绝对偏差的一种,在估计尺度参数时,对称分布中后者更稳健,在非对称分布中前者更稳健。
,用样本中位数,估计μ。这两种估计量均是中位数绝对偏差的一种,在估计尺度参数时,对称分布中后者更稳健,在非对称分布中前者更稳健。
Huber在1981年[2] 提了t为估计量,F为分布函数,t在F处的影响函数为
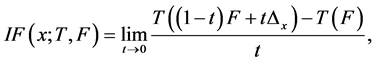
其中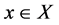 极限存在。
极限存在。
由于影响函数与得分函数程正相关,本文用得分函数来求。这里引用了参考文献[5] 中的公式作为得分函数
 (1)
(1)
这里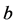 是满足费希尔一致性条件
是满足费希尔一致性条件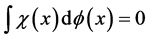 的常数,
的常数,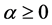 为自由参数,
为自由参数,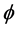 是标准正态分布函数。
是标准正态分布函数。
由泰勒展开式
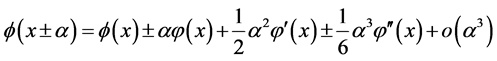 (2)
(2)
这里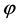 为标准正态分布密度函数。
为标准正态分布密度函数。
由于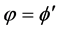 ,
, ,
,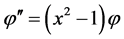 ,并将(2)代入(1)得
,并将(2)代入(1)得
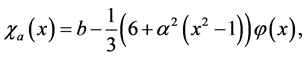 (3)
(3)
其中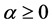 ,由费希尔一致性条件
,由费希尔一致性条件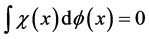 ,将(3)代入费希尔一致性条件,
,将(3)代入费希尔一致性条件,
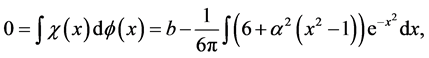
由此得,
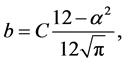
其中C为常数
由牛顿–辛普森一步迭代公式 知一步M估计
知一步M估计
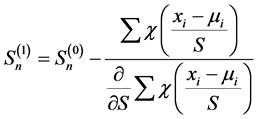
在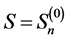 处,其中
处,其中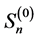 为初始估计,所以
为初始估计,所以
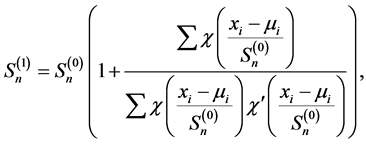
将(3)代入上式
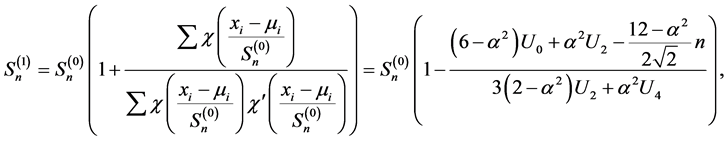 (4)
(4)
其中
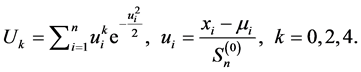
用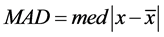 作为估计的初始值,
作为估计的初始值,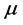 用
用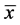 估计,代入(4)式,得
估计,代入(4)式,得
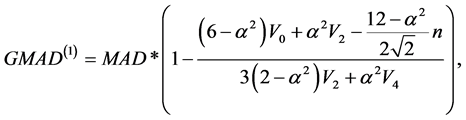
其中
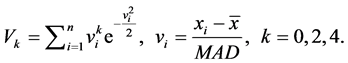
用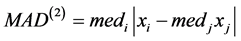 作为估计的初始值,
作为估计的初始值,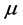 用
用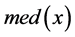 估计,代入(4)式,得
估计,代入(4)式,得

其中
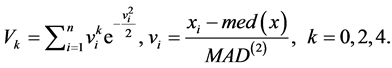
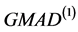 和
和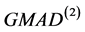 统称为GMAD。
统称为GMAD。
由于 为自由参数,不妨设
为自由参数,不妨设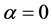 ,则GMAD可简化为
,则GMAD可简化为
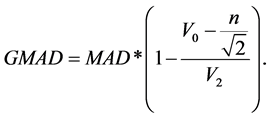
3. 蒙特卡罗模拟
受污染分布描述为[1] :
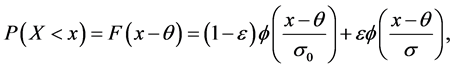
其中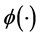 表示标准正态分布函数,
表示标准正态分布函数,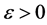 是一个比较小的数,相应于异常观测值在全部观测值中所占的比例,而
是一个比较小的数,相应于异常观测值在全部观测值中所占的比例,而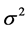 可能比
可能比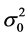 大许多(或小许多)。由于粗差出现的概率为1%~10%,故而实验中
大许多(或小许多)。由于粗差出现的概率为1%~10%,故而实验中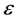 取0.1。
取0.1。
3.1. 蒙特卡罗模拟结果图形
图1~5均为自由参数 ,
,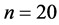 ,重复10,000次的结果。
,重复10,000次的结果。
图1为这几种尺度估计量在没有受到污染,且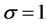 时的正态分布中变化情况图。由此图可知在没受到污染的正态分布中,sd最接近1,稳健性最好。其次是
时的正态分布中变化情况图。由此图可知在没受到污染的正态分布中,sd最接近1,稳健性最好。其次是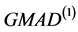 和
和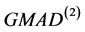 ,他们几乎是重合的,说明他们的估计尺度的稳健性几乎无差别。再者是IQR和MAD,他们的估计稳健性也差不多。然后是
,他们几乎是重合的,说明他们的估计尺度的稳健性几乎无差别。再者是IQR和MAD,他们的估计稳健性也差不多。然后是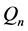 ,虽有所偏离,但也在可承受范围内。我们能明显看出FQ的不同,在均值为0时,FQ估计尺度的稳健性非常好,但在均值非0时,有明显的偏离,均值的绝对值越大,偏离程度越大,且偏离程度是对称的。
,虽有所偏离,但也在可承受范围内。我们能明显看出FQ的不同,在均值为0时,FQ估计尺度的稳健性非常好,但在均值非0时,有明显的偏离,均值的绝对值越大,偏离程度越大,且偏离程度是对称的。
图2为各个尺度估计量在受污染的,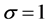 ,
, 的正态分布中的变化情况图。由图2可看出,在受污染的正态分布中,
的正态分布中的变化情况图。由图2可看出,在受污染的正态分布中, 与
与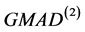 估计尺度参数最接近1,且它们几乎重合,说明它们估计尺度参数时的稳健性几乎差不多,且是这几个尺度估计量里估计尺度最好的。
估计尺度参数最接近1,且它们几乎重合,说明它们估计尺度参数时的稳健性几乎差不多,且是这几个尺度估计量里估计尺度最好的。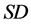 估计尺度参数要比在没受污染的正态分布中要差些,其它的估计几乎与在没受污染的正态分布中估计几乎没什么差别。
估计尺度参数要比在没受污染的正态分布中要差些,其它的估计几乎与在没受污染的正态分布中估计几乎没什么差别。
由于伽马分布在形状参数 ,
,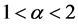 ,
,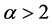 时,对应的伽马密度曲线形状不同,故而在伽
时,对应的伽马密度曲线形状不同,故而在伽
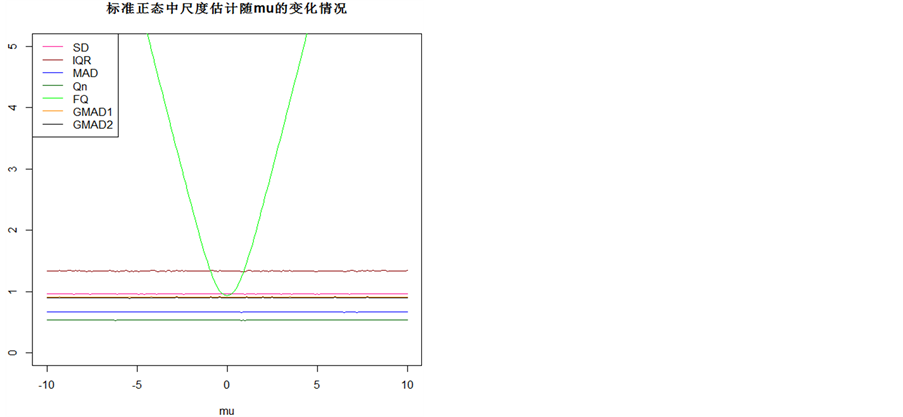
Figure 1. Scale estimators based on the mean of the standard normal distribution
图1. 尺度估计量在标准正态分布中随均值变化图
马分布中的尺度估计量分这三种情况进行讨论,即图3、图4、图5。
由图3可明显看出,这几种估计在形状参数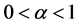 时,都不可行。
时,都不可行。
由图4可知,在形状参数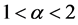 时,除了估计量
时,除了估计量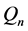 的估计效果不佳外,其它的几个估计稳健性都挺好。SD最接近
的估计效果不佳外,其它的几个估计稳健性都挺好。SD最接近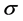 ,稳健性最强,其次估计量IQR与新的估计量
,稳健性最强,其次估计量IQR与新的估计量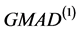 稳健性也非常好,估计量fq估计尺度时虽不如
稳健性也非常好,估计量fq估计尺度时虽不如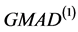 ,但也相对不错了,
,但也相对不错了,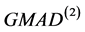 与MAD在此种情况下用来估计尺度也是可行的。
与MAD在此种情况下用来估计尺度也是可行的。
由图5可明显看出在形状参数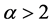 时,估计量fq明显偏离准确尺度参数
时,估计量fq明显偏离准确尺度参数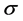 许多,说明此种估计根本不可行。估计量iqr也偏离准确尺度2倍,所以也不可行。其他的估计量都在允许范围内,且在这几种估计量估计尺度参数时,MAD最为稳健,其次是
许多,说明此种估计根本不可行。估计量iqr也偏离准确尺度2倍,所以也不可行。其他的估计量都在允许范围内,且在这几种估计量估计尺度参数时,MAD最为稳健,其次是 ,然后是
,然后是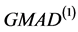 与
与 ,最后是sd。
,最后是sd。
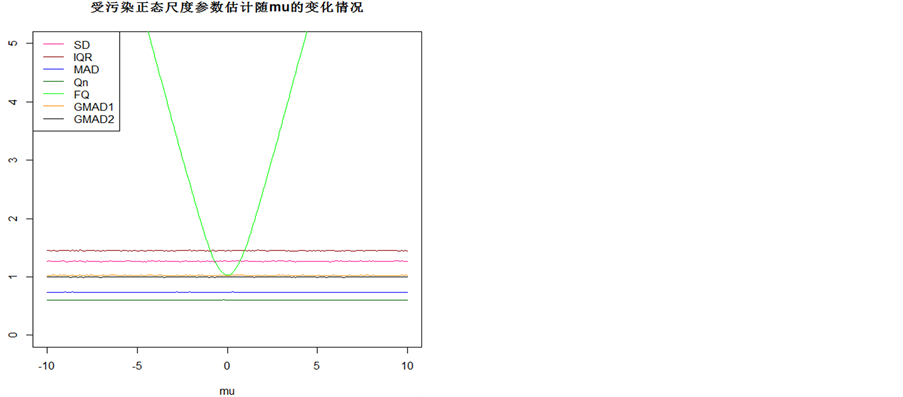
Figure 2. Scale estimators based on the mean of the contaminated normal distribution
图2. 尺度估计量在受污染正态分布中随均值变化图

Figure 3. Scale estimation based on the gamma distribution of the shape parameter is from 0 to 1
图3. 尺度估计量在形状参数为0~1的伽马分布中变化图
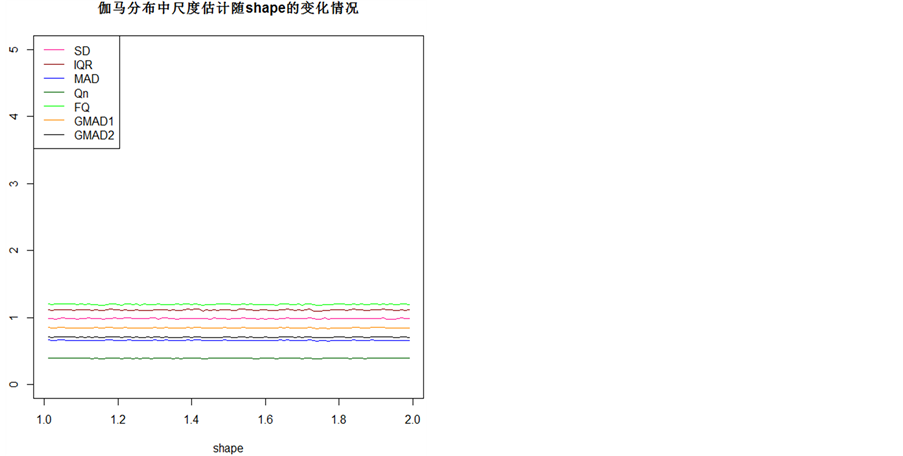
Figure 4. Scale estimators based on the Gamma distribution of the shape parameter is from 1 to 2
图4. 尺度估计量在形状参数为1~2的伽马分布中变化图
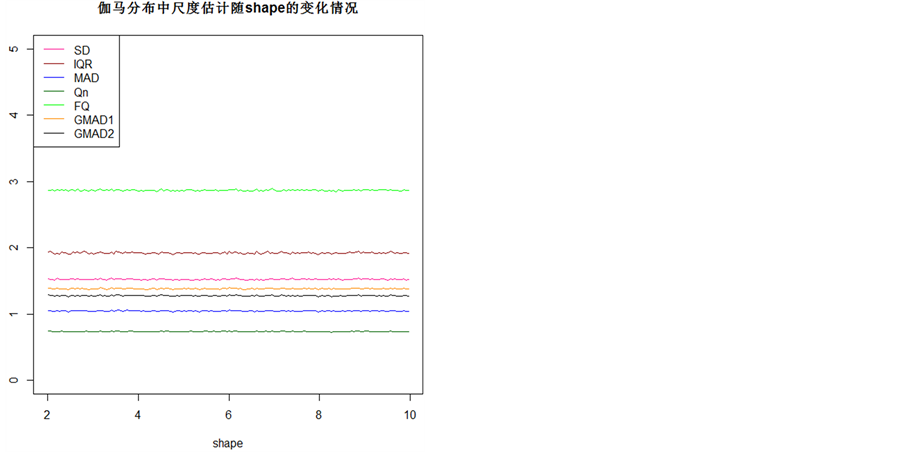
Figure 5. Scale estimators based on the gamma distribution of the shape parameter is greater than 2
图5. 尺度估计量在形状参数大于2的伽马分布中变化图
由图我们可知,无论是在没有受到污染的正态分布中,还是在受到污染的正态分布中,新估计量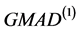 与
与 在估计尺度参数
在估计尺度参数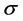 时,都非常稳健,而估计量fq只有在均值为0时稳健。在伽马分布中,这几种估计量在形状参数
时,都非常稳健,而估计量fq只有在均值为0时稳健。在伽马分布中,这几种估计量在形状参数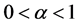 的情形下均不稳健;在形状参数
的情形下均不稳健;在形状参数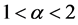 的情形下,除了估计量
的情形下,除了估计量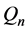 的稳健性不佳外,其它的几个估计量估计尺度参数时的稳健性都挺好;在形状参数
的稳健性不佳外,其它的几个估计量估计尺度参数时的稳健性都挺好;在形状参数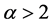 的情形下,估计量fq与IQR非常不稳健,不能用来估计尺度参数,其它几个估计量均比较稳健。
的情形下,估计量fq与IQR非常不稳健,不能用来估计尺度参数,其它几个估计量均比较稳健。
3.2. 蒙特卡罗模拟结果表
表1~3均是自由参数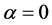 ,每个
,每个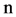 都重复试验10,000次的结果。
都重复试验10,000次的结果。
由表1可知,在均值为0的受污染的正态分布中,估计量FQ、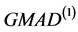 、
、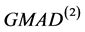 估计尺度参数时的稳健性几乎没什么差别,都很好。其它四中估计量估计尺度的偏差也都在可承受范围内。
估计尺度参数时的稳健性几乎没什么差别,都很好。其它四中估计量估计尺度的偏差也都在可承受范围内。
表2为形状参数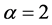 ,尺度参数
,尺度参数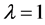 时的情况,此时估计量FQ、
时的情况,此时估计量FQ、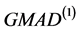 、
、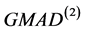 估计尺度参数时的稳健性都很好。其中
估计尺度参数时的稳健性都很好。其中 比FQ好些,FQ比
比FQ好些,FQ比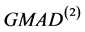 好些。
好些。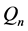 超出了可承受范围。
超出了可承受范围。
表3说明在指数分布中,估计量FQ非常稳健,估计量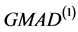 虽不如FQ,但也很稳健。估计量
虽不如FQ,但也很稳健。估计量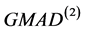 估计尺度参数的稳健性虽差些,但也在可承受范围内。
估计尺度参数的稳健性虽差些,但也在可承受范围内。
由表可知,对于均值为0时,在受污染的正态分布模型的情况下,FQ与gmda的稳健性差不多。在非正态分布下的情形,如在形状参数为2时的伽马分布中,FQ与gmda均可用,稳健性FQ虽不如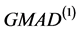 好,但比
好,但比 要好。在指数分布中,估计量FQ非常稳健,估计量
要好。在指数分布中,估计量FQ非常稳健,估计量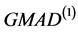 虽不如FQ,但也很稳健。估计量
虽不如FQ,但也很稳健。估计量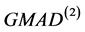 估计尺度参数的稳健性虽差些,但也在可承受范围内。
估计尺度参数的稳健性虽差些,但也在可承受范围内。

Table 1. The mean of contaminated normal distribution is 0 (ε = 10%, σ = 1, σ* = 3σ)
表1. 均值为0的受污染正态分布(ε = 10%, σ = 1, σ* = 3σ)

Table 2. Gamma distribution (α = 2, λ = 1)
表2. 伽马分布(α = 2, λ = 1)

Table 3. Exponential distribution (λ = 1)
表3. 指数分布(λ = 1)
4. 结论
由以上分析可知,正态分布模型无论有没有受到污染,新的估计量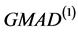 与
与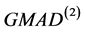 在估计尺度参数
在估计尺度参数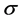 时,都非常稳健,且它们的差异性不大,而估计量FQ只有在均值为0时才稳健。均值为正或负对估计的稳健性并没有影响,而均值的绝对值的大小对估计量FQ影响较大,对其它估计量也没什么影响。
时,都非常稳健,且它们的差异性不大,而估计量FQ只有在均值为0时才稳健。均值为正或负对估计的稳健性并没有影响,而均值的绝对值的大小对估计量FQ影响较大,对其它估计量也没什么影响。
在非正态分布下的情形,如伽马分布、指数分布等估计量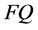 与新的估计量
与新的估计量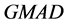 也是可用的。在线性模型中是否可用还有待研究。
也是可用的。在线性模型中是否可用还有待研究。
致谢
本文是在我的导师李再兴老师的指导完成的。此外,本文得到中央高校基本科研业务费以及北京市青年英才计划的资助。